界面对SiCf/BN/SiC复合材料纤维顶出过程影响的有限元模拟

高 晔，束小文，吕晓旭，周怡然，姜卓钰，董禹飞，贺宜红，焦 健

(1.中国航发北京航空材料研究院先进复合材料国防科技重点实验室，北京 100095； 2.陆军装备部航空军事代表局， 北京 100101； 3.中国航发湖南动力机械研究所，湖南 株洲 412002)

1 前 言

碳化硅陶瓷基(SiCf/SiC)复合材料因其耐高温、抗氧化、抗热震、比强度高等特点，适于在高温环境中长时使用，被认为是未来先进航空发动机热端部件的首选材料，近年来越来越受到国内航空领域从业者的重视[1]。SiCf/SiC复合材料主要由SiC增强纤维、界面层与SiC基体三部分组成，其中界面层作为纤维与基体之间的“桥梁”，设计合理的界面层可以起到偏转基体裂纹、吸收断裂能、保护纤维进而保障纤维拔出等作用，对复合材料的性能有至关重要的作用[2，3]。

与裂解碳界面层相比，氮化硼(BN)界面层由于氧化后生成BN，可有效阻止碳化硅纤维氧化失效[4]。Rice[5]于20世纪80年代在陶瓷基复合材料中引入了BN界面层，大幅提高了其抗高温性能。由于界面层厚度仅在亚微米尺度，通过试验手段难以直接对界面层的性能进行评估，需通过纤维拔出、纤维顶出、微粒脱粘试验等手段间接进行研究，其中，又以纤维顶出或纤维拔出等试验手段最为典型[6]。Lu等[7]通过SiCf/BN/SiC mini复材的纤维顶出试验及拉伸强度试验，对mini复材的氧化现象和不同氧化温度下BN界面层的界面强度进行了研究。Kececi等[8]对四种不同纤维增强的复合材料开展了纤维顶出试验，对其失效模式及结合强度进行了试验研究。从试验过程及结果分析发现，由于纤维直径通常在微米级，特别是对SiCf/BN/SiC复合材料而言，SiC基体为硬、脆材料，导致纤维顶出试验件制备难度大、试验成功率低、试验数据分散性大且分析复杂，给试验结果分析的可靠性带来了很大干扰[9]。因此越来越多学者借助有限单元法对纤维拔出的过程进行研究，如Bahl[10]、You等[11]、李巾锭等[12]均采用了有限元法分别对铝基复合材料、铜基复合材料、C/SiC复合材料的纤维拔出过程进行了模拟，然而针对SiCf/BN/SiC复合材料纤维拔出的有限元模拟还未见报道。

本研究在前人研究基础上，根据文献[7]的试验过程与试验结果，建立SiCf/BN/SiC复合材料单纤维顶出过程的有限元分析模型，同时考虑了制备过程中热残余应力的影响。基于该模型进一步研究了界面层临界断裂能、极限强度和厚度对纤维顶出过程的影响。

2 纤维顶出有限元分析模型

2.1 界面层模拟方法

界面层采用内聚力单元(cohesive element)进行模拟，其本构模型为双线性traction-separation模型，如图1所示，包括线弹性阶段及达到极限强度后的刚度线性降低阶段。

在线弹性阶段，材料的本构关系可表示为式(1)：

(1)

当粘合力达到极限强度t0时，内聚力模型以最大名义应力准则发生初始损伤，如式(2)：

(2)

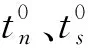
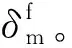
(3)

(4)

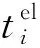
(5)

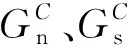
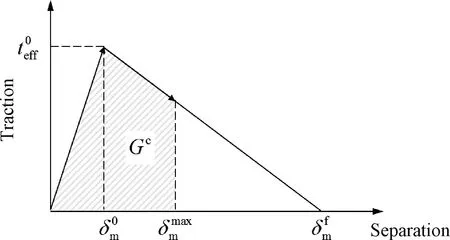
图1 内聚力单元的双线性traction-separation模型Fig. 1 Bilinear traction-separation law for cohesive element

2.2 纤维顶出有限元模型

根据文献[7]中单纤维顶出试验件尺寸及试验过程，采用商用有限元分析软件ABAQUS，建立了SiCf/BN/SiC复合材料单纤维顶出的有限元分析模型，模型几何示意图如图2所示。模型由压头、试验件和支撑平面组成，其中试验件由SiC纤维、BN界面层、SiC基体及SiCf/BN/SiC复合材料组成，纤维体积分数为45%。试验件高度、纤维直径及界面层厚度均与文献[7]中尺寸一致。为提高计算效率，采用二维轴对称模型进行计算，压头及支撑平面设置为刚性面，同时对试验件面内尺寸进行了适当缩小。

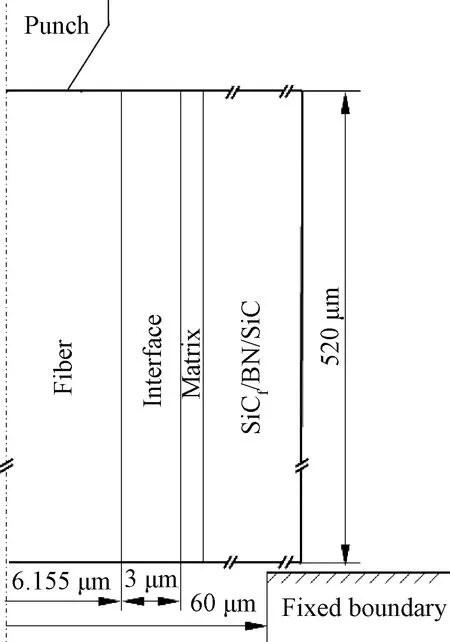
图2 纤维拔出几何模型示意图Fig. 2 Geometry model of the fiber push-out test

有限元模型网格如图3所示，界面层单元类型为COHAX4，其中纤维、基体与复合材料为自由网格，单元类型为CAX4R。由于内聚力单元的特点，界面层单元在厚度方向网格数量为1；为保证计算结果可靠性，内聚力模型网格长宽比不超过3∶1。

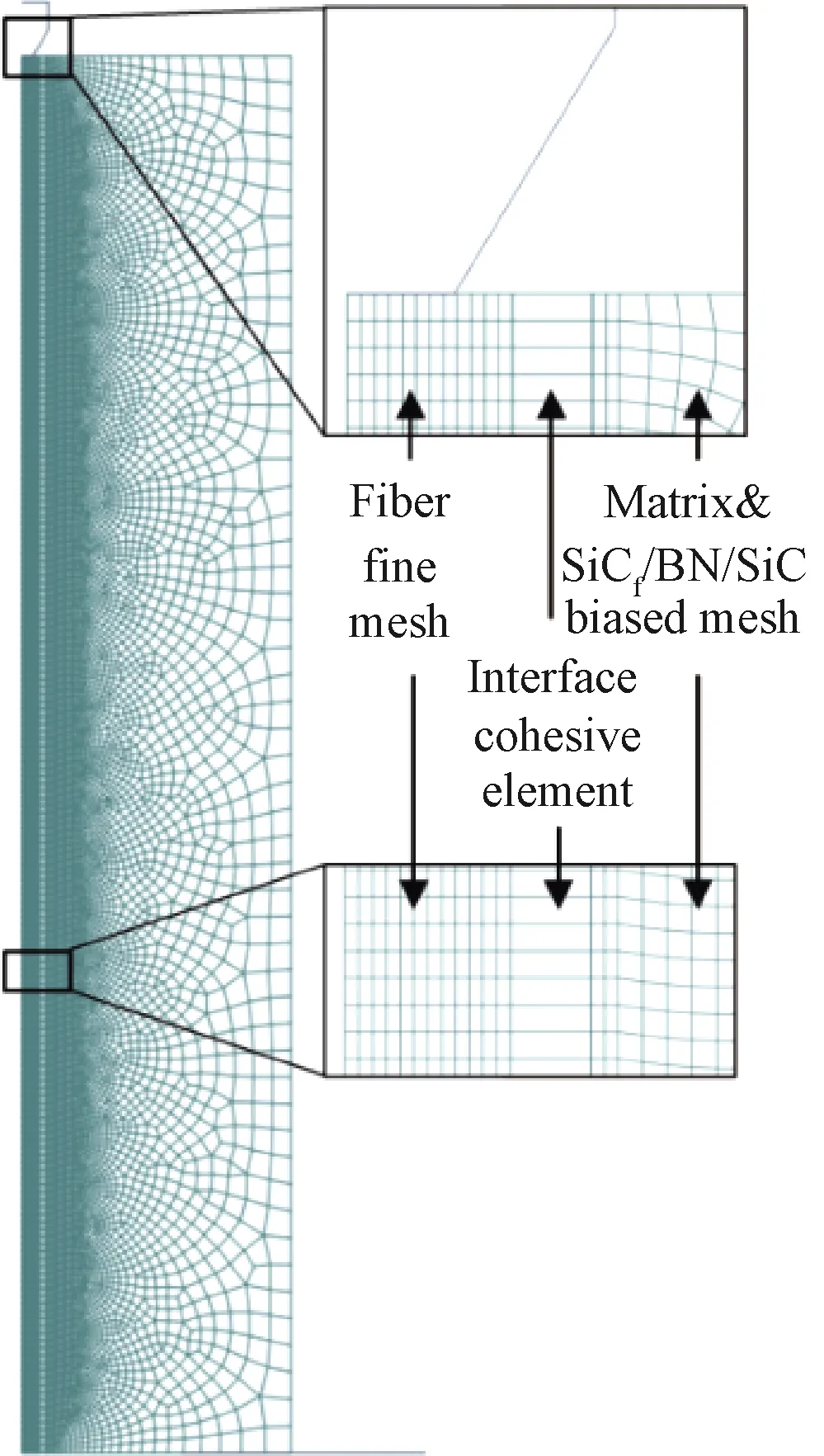
图3 有限元模型网格划分示意图Fig. 3 Mesh of the finite element analysis model

SiCf/BN/SiC复合材料单纤维顶出的有限元分析过程分为两步：第一步考虑SiC基体在1100 ℃制备后冷却到室温时产生的热残余应力，为自由热膨胀过程；第二步在压头顶端施加轴向位移，将SiC纤维沿轴向顶出。将纤维、基体和复合材料视为各向同性线弹性材料，其材料性能参数见表1，BN界面层材料性能参数见表2[13]。

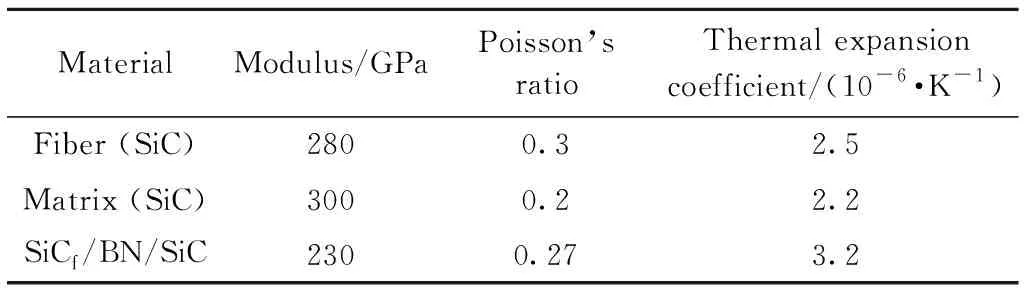
表1 SiC纤维、SiC基体与SiCf/BN/SiC复合材料材料属性Table 1 Material properties for SiC fiber, SiC matrix and SiCf/BN/SiC composites

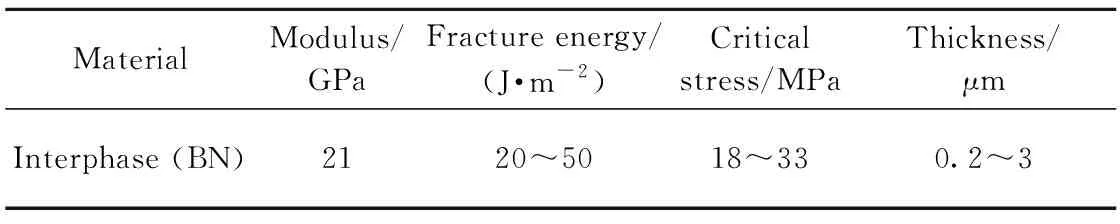
表2 BN界面层材料属性Table 2 Material properties for BN interphase

3 模拟结果分析

本研究得到的SiCf/BN/SiC复合材料单纤维顶出载荷位移曲线如图4所示，可见曲线无明显的线性段[11，12]，其原因可能是由于本研究建立的模型厚度与纤维直径之比较大。可将该曲线分为三个阶段。当压头压入纤维，界面层顶部单元在接近失效时(即D≈1，且D<1)，底部单元仍无损伤产生(见图5)，因此第一阶段表现为非线性；当载荷逐渐增大时，整个界面层单元损伤逐渐累积直至失效(D=1)，此时界面层完全脱粘，压头载荷发生突变，即图4与图5第二阶段；在第三阶段，由于纤维与基体之间界面已完全脱粘，仅需很小的力即可将纤维顶出。本模拟得到的纤维最大顶出力为395 mN，与文献[7]中对应试验结果402 mN仅相差1.74%，证明了模拟方法的有效性，因此可在该模型基础上进行界面层参数的研究。

在应用机器视觉的方法中,首先需要从图像中提取出长方体可见的边线或顶点特征,再通过计算特征间距离实现测量。对于长方体边线的提取,典型方法是采用Hough变换从原始图像或原始图像的校正图像中获取直线方程[9],受相机透视投影的影响,长方体边线间的平行和垂直关系在原始图像的校正图像中都不成立,一般是利用消失点和消失线确定直线间的平行关系[1-3,10-11],因此直线间固有的约束不易被利用,容易导致特征提取出现偏差,影响测量精度。

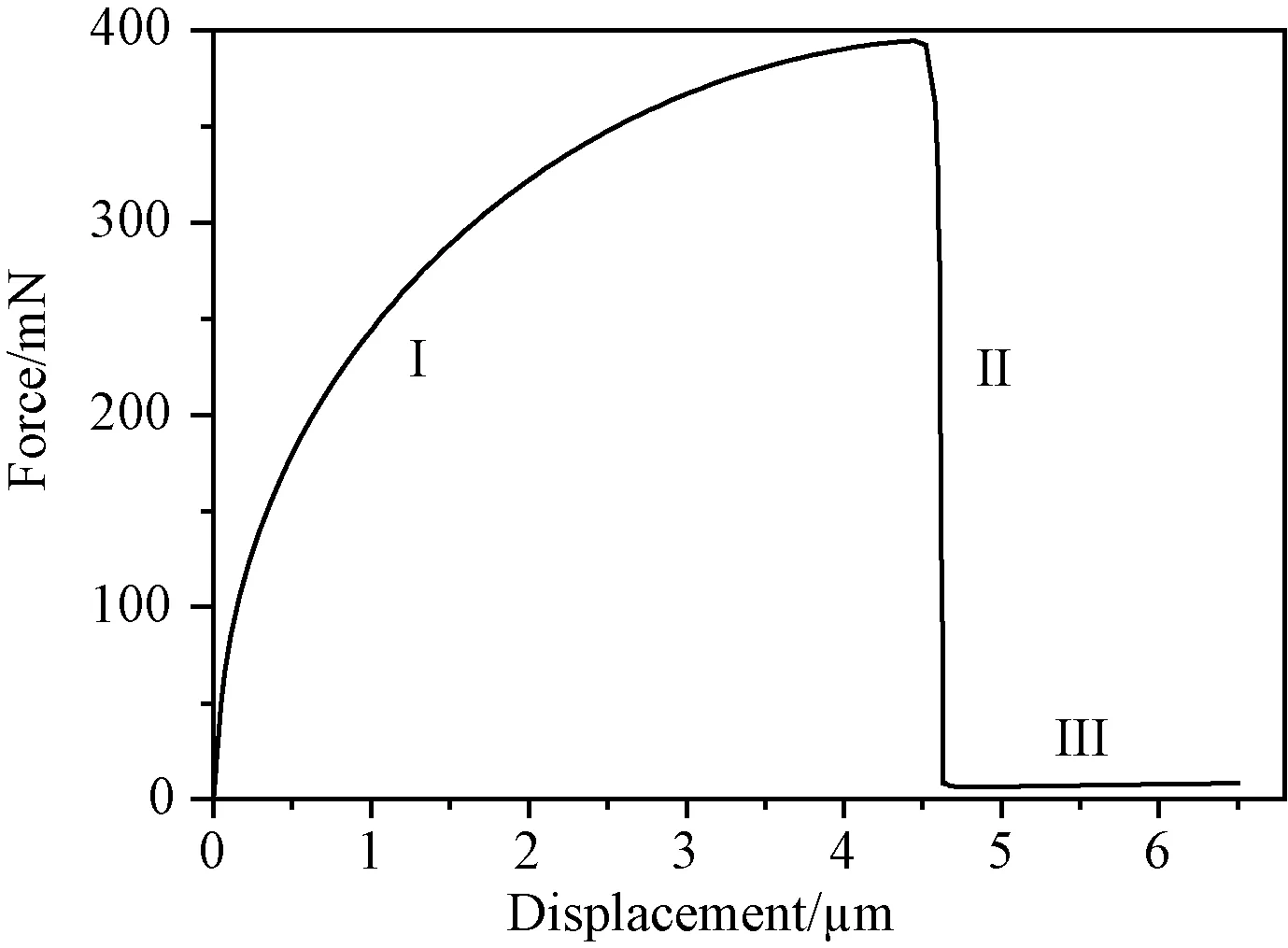
图4 纤维顶出载荷-位移模拟曲线Fig. 4 Force-displacement curve of the fiber push-out simulation

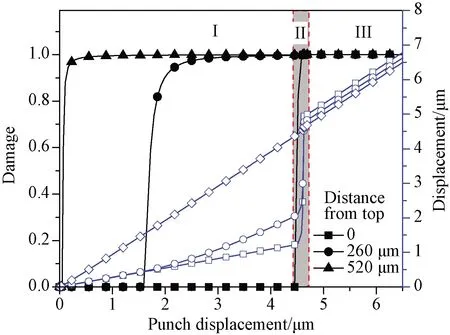
三组符号“■、□”，“●、○”，“▲、△”分别表示距顶面距离为0、260、520 μm； 实心符号表示左坐标数值，空心符号表示右坐标数值图5 界面层单元损伤与位移随压头压入深度的变化Fig. 5 Curves of cohesive element damage and displacement with punch displacement

3.1 临界断裂能对顶出过程的影响

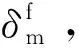
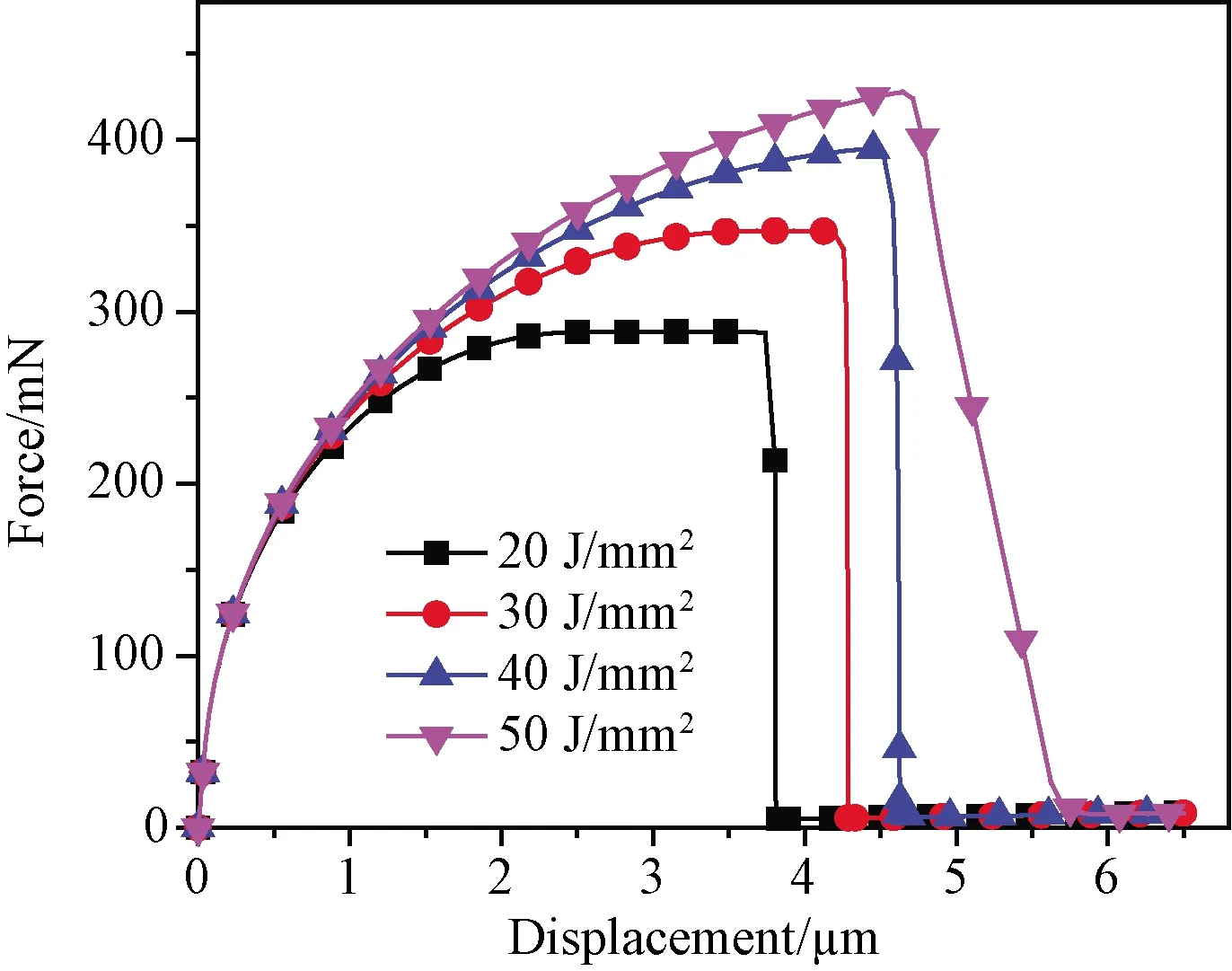
图6 界面层临界断裂能对载荷-位移曲线的影响Fig. 6 Force-displacement curves of varying critical energy

需要注意的是，当临界断裂能取最小值20 J/mm2时，载荷-位移曲线在顶端出现了平直段，即压头位移增加，而顶出载荷不变，其原因可能在于界面层的断裂形变较小，其值为1.7 μm，在压头压入纤维过程中，界面层顶端单元即已完全脱粘，随后沿着纤维轴向完全脱粘。因此在实际材料制备过程中，需保证界面层适当的结合强度，使其既能起到纤维增韧、又可起到偏转基体裂纹的作用。

3.2 界面层极限强度对顶出过程的影响

界面层单元极限强度对载荷～位移曲线的影响如图7所示，可以看出，当界面层极限强度增加时，在第一阶段，压头移动相同位移所需要的载荷也有所增加，因为纤维滑动(即单元到达刚度软化阶段)所需要的载荷需满足界面层单元应力超过其极限强度。

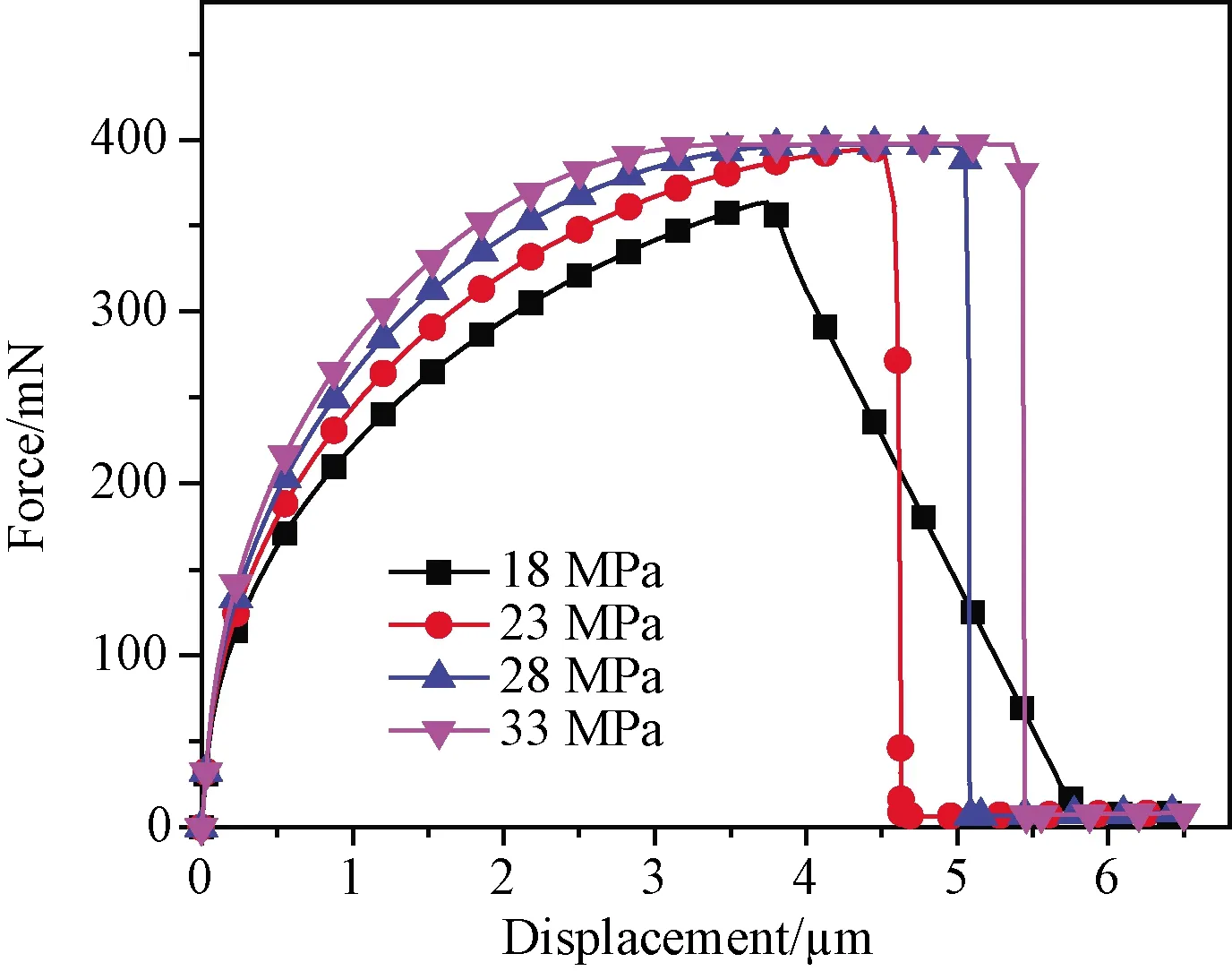
图7 界面层极限强度对载荷-位移曲线的影响Fig. 7 Force-displacement curves of varying interphase strength

当界面层极限强度为最小值18 MPa时，载荷～位移曲线第二阶段的载荷突变效应不明显，结合图1分析可知，临界断裂能固定不变时，界面层单元断裂形变与极限强度呈反比。当极限强度较小时，界面层断裂形变较大，这就意味着，压头压入纤维时，界面层单元很快进入刚度软化阶段，但由于断裂形变较大(其值为4.4 μm)，界面层单元在刚度显著降低后还仍会将基体和纤维“粘连”到一起，而不会完全脱粘，因此载荷突变效应不明显；同理，当临界断裂能较大时，断裂形变也较大，同样会导致载荷突变效应不明显，如图7中临界断裂能为50 J/mm2(此时断裂形变为4.3 μm)时所示。当极限强度从18 MPa增加到23 MPa时，纤维最大顶出载荷从363 mN增加到395 mN，载荷～位移曲线第二阶段的载荷突变效应明显，此后其变化对纤维最大顶出载荷的影响不大。由此可见，在实际材料制备过程中，无需过多关注BN界面层是否开始脱粘。

当极限强度为最大值33MPa时，载荷-位移曲线在顶端也会出现平直段，这与临界断裂能取最小值时的影响相同，同样是由于界面层单元断裂形变较小(其值为2.4 μm)所致。

3.3 界面层厚度对顶出过程的影响

文献[7]中为了研究BN界面层的氧化效应，将其厚度控制住3 μm，与SiCf/SiC复合材料常用界面层厚度100 ～ 500 nm相差较大，因此进一步研究了界面层厚度对载荷-位移曲线的影响，模拟结果如图8所示。

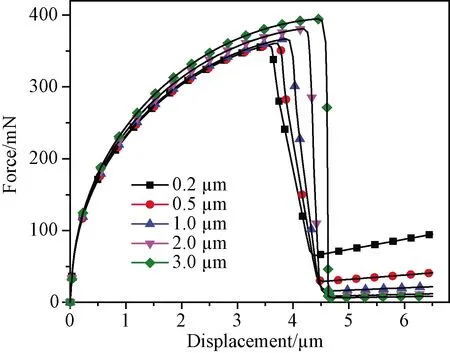
图8 界面层厚度对载荷-位移曲线的影响Fig. 8 Force-displacement curves of varying interphase thickness

界面层厚度为0.2 μm时，载荷-位移曲线在载荷下降后的第三阶段略有上升，这是由于压头与基体发生接触引起的。当界面层厚度从0.2 μm增加到3 μm时，纤维最大顶出载荷从358 mN增加到395 mN，增加幅度为10.3%，由此可见界面层厚度对纤维最大顶出载荷的影响不大。需要指出的是，本研究在改变界面层厚度时，默认其性能参数不变，而实际上BN界面层具有与石墨结构类似的层状结构，其厚度的改变可能导致模量、临界断裂能等参数也发生相应的改变，这后续研究尚需结合更进一步的试验结果加以验证。

4 结 论

1．基于双线性traction-separation模型的内聚力单元，建立了SiCf/BN/SiC复合材料单纤维顶出过程的有限元仿真模型，模拟得到的纤维顶出最大载荷与文献[7]的试验结果仅相差1.74%，充分证明了本研究有限元仿真模型的有效性。

2．基于建立的有限元仿真模型，模拟得到的载荷-位移曲线可能会在载荷最大时出现平直段，这可能是由于本研究建立的模型较厚，而界面断裂应变值较小，导致界面层底部单元未产生损伤时，顶部单元即已完全脱粘所致。

3．临界断裂能对纤维顶出最大载荷的影响较大，而界面层厚度对其影响较小，极限强度对其影响不大。综上所述，在实际材料制备过程中，无需过多关注界面层是否开始脱粘，而应重点控制界面层的临界断裂能。