基于不确定理论的丝杠预紧力退化可靠性建模*

龚梦辉，周长光，周华西，韩 军，冯虎田

(1.南京理工大学机械工程学院，南京 210094；2.数控机床功能部件性能测试评价与可靠性技术重点实验室，苏州 215600)

0 引言

滚珠丝杠副是一种能够实现旋转运动和直线运动相互转换的滚动功能部件，因其高效率、高精度等特点，已被广泛应用于精密机械、航空航天、船舶、核工业等重要领域。滚珠丝杠副在使用过程中会因为磨损导致预紧力的退化或丧失，导致刚性和承载力降低，甚至会产生轴向间隙，降低其精度，可以说，预紧力在很大程度上决定着滚珠丝杠副的使用寿命。因此，通过研究预紧力的退化过程，实现对滚珠丝杠副的寿命可靠性分析，对于滚珠丝杠副的维护和保养具有重要参考意义。

随着科技的发展，对滚珠丝杠副的可靠度水平要求不断提高，其使用寿命也大大延长，传统基于寿命数据的可靠性试验评估方法周期较长，不利于产品的研发，因此基于加速退化试验(accelerated degradation testing,ADT)的可靠性评估方法应运而生[1]。束芳婷[2]建立了等效加速失效模型，并对滚珠丝杠副进行了步进加载可靠性加速试验和可靠性分析。张筱辰[3]设计了一种加速寿命退化实验装置，建立了寿命预测模型。赵哲[4]基于三水平恒定应力进行了加速性能退化实验和寿命预测。唐圣金等[5]基于维纳过程(Wiener process,WP)提出了一种步进应力加速退化模型和剩余寿命估计方法。吴晓辉、蔡忠义等[6-7]基于维纳过程建立了考虑非线性和随机效应的加速退化模型。盖炳良等[8]在建立加速退化模型时都遵循加速因子不变原则，从而消除了主观经验的影响。ELRAHEEM[9]对多重恒应力加速寿命进行了优化设计。

由于ADT所需样本少，只能获得对产品少量信息，缺乏对其整体的了解，从而产生认知不确定性。上述加速退化试验模型或方法大部分都基于维纳过程或贝叶斯理论，以概率论为基础，需以大数定律作为支撑。对于小样本数据，在估算时会导致其概率分布偏离长期累积频率，从而导致评估失效，因此概率论不再适用[1]，且上述方法很多未考虑认知不确定的影响。而不确定性理论(uncertainty theory,UT)能够反映和量化认知不确定性，因此，将不确定理论引入数据处理领域也是一个趋势。LI等[10]基于刘过程，提出了一种不确定加速退化框架，并给出了参数的不确定统计方法。LI等[11]针对有限和截尾的失效时间数据，提出了基于不确定性理论的寿命模型和可靠性评估方法。康锐[1]在此基础上更加详细地阐述了确信可靠性理论在加速退化试验中的应用。

滚珠丝杠副的预紧力退化受很多参数影响，而这些参数由于人们的认知的偏差而存在认知不确定性。本文引入不确定理论，基于预紧力退化来建立考虑认知不确定性的滚珠丝杠副加速退化模型，并在此基础上建立滚珠丝杠副寿命的可靠性计算模型。

1 滚珠丝杠加速退化寿命可靠性建模

本节以滚珠丝杠副预紧力退化为研究对象，提出了一种基于不确定理论加速退化寿命可靠性评价模型，包括加速退化模型和加速退化可靠性模型。

1.1 加速退化模型

加速退化试验的思想就是利用高应力的寿命特征取推导正常应力得寿命特征[12]，实质上就是通过一个应力水平的试验数据去推导另一应力水平的寿命特征。因此，关键在于建立滚珠丝杠副寿命特征与应力水平之间的关系，即加速退化模型。

现阶段，常用的加速模型有阿伦尼斯(Arrhenius)模型、幂律模型、单应力的艾林(Egring)模型、广义艾林模型、指数模型等。根据文献[13-14]可知，对于指数模型、幂律模型、阿伦尼斯模型这三种加速退化模型，可统一定义为：

e(s)=aexp(bs)

(1)

式中，e(s)为寿命-应力模型[15]，即加速退化模型，表征预紧力退化速率；常数a在退化中表示样本维度的不确定因子，服从正态不确定分布，即a～Nu(μa,σa)，μa>0，σa>0；b为常数项，b>0；s为应力加速因子，也叫归一化应力。

当考虑滚珠丝杠副应力水平的认知不确定时，式(1)变为：

e(s)=aexp(bs)+σsξs

(2)

式中，σs为常数；ξs为表征应力水平不确定性的不确定因子，服从均值为0，标准差为s的正态不确定分布，即ξs～Nu(0,s)。

因此，给定s后，e(s)服从正态不确定分布：

(3)

在加速退化模型中，应力加速因子表征产品在加速应力下寿命特征值与正常应力下寿命特征值的比例关系，反映加速退化试验中某加速应力水平的加速效果，即是加速应力的函数[12]。根据研究，对于滚珠丝杠副，其应力加速因子不仅依赖于寿命分布，还依赖于应力水平间的折算原则。

不同的加速退化模型，对应的应力加速因子函数也不同。根据文献[16]，对于阿伦尼斯模型，其应力加速因子为：

(4)

式中，sl为第l个应力的应力加速因子；Sl为第l个应力的实际应力水平；SL和SU分别为滚珠丝杠副应力水平下限和上限。

对于幂律模型，其应力加速因子为：

(5)

对于指数模型，其应力加速因子为：

(6)

1.2 基于不确定理论的加速退化可靠性建模

滚珠丝杠副的预紧力会随着时间积累而逐渐退化，其退化量也会逐渐增加，且不同应力水平下其退化情况也不相同，因此，滚珠丝杠副的预紧力、预紧力退化量都是应力水平和时间的函数，其退化方程为：

(7)

X(s,t)=e(s)t+σC(t)

(8)

考虑非线性退化情况，将上式中的t用时间尺度函数tβ替代得：

X(s,t)=e(s)tβ+σCt

(9)

式中，σ为扩散系数；Ct为不确定过程，服从期望为0，标准差为tβ的正态不确定分布；β为非线性系数，且σ>0，β>0。

联立式(2)、式(9)得预紧力退化量函数为：

X(s,t)=[aexp(bs)+σsξs]tβ+σCt

(10)

式中，a～Nu(μa,σa)；ξs～Nu(0,s)；Ct～Nu(0,tβ)。

当s和t已知时，预紧力退化量函数服从正态不确定分布：

(11)

联立式(7)和式(10)得滚珠丝杠副预紧力的退化方程为：

Y(s,t)=Y0-{[aexp(bs)+σsξs]tβ+σCt}

(12)

当滚珠丝杠副的预紧力阈值Yth已知时，其性能裕量方程为：

M(s,t)=IY(Yth-Y(s,t))=IY(Yth-Y0)-[aexp(bs)+σsξs]tβ-σCt

(13)

设滚珠丝杠副的预紧力退化量阈值为Xth，有：

Yth=Y0-Xth

(14)

联立式(13)、式(14)有：

M(s,t)=Xth-[aexp(bs)+σsξs]tβ-σCt

(15)

当s和t已知时，预紧力的裕量方程也服从正态不确定分布：

(16)

在不确定理论中，可靠度R为性能裕量大于0的信度[17]，即：

R(s,t)=Ch{M(s,t)>0}=1-γ(s,t)

(17)

式中，γ(s,t)为不可靠度函数，在不确定理论中，其表示裕量方程首次穿过临界值0的时刻tc所服从的不确定分布，概率分布函数为：

γ(s,t)=Ch{tc≤t}=

(18)

联立式(17)和式(18)得滚珠丝杠副的寿命确信可靠度为：

(19)

2 模型参数估计

根据上文建立的基于不确定理论的加速退化可靠性模型，需要进行估计的未知参数有θ=(σ,β,μa,σa,b,σs)。在概率统计中，常用的参数估计方法为极大似然法，采用极大似然法首先需要知道参数的概率密度函数，但是，在不确定理论中，不存在概率密度，只存在分布函数，因此，极大似然法不再适用。事实上，性能退化量数据与其信度是存在关系的，根据风险分析理论，性能退化量越大，其信度也越大[1]，因此，本文采用基于风险分析理论的参数估计方法对未知参数进行估计。

在经典统计分析中，通常采用经验分布函数法来计算性能退化量函数的信度，设第l个应力水平sl下第i支滚珠丝杠的第j个预紧力退化值为xlij，应力水平sl下丝杠的样本数为Nl，试验应力水平个数为p，应力水平sl下第i支丝杠的预紧力退化量检测次数为mli。根据文献[1]和文献[18]，信度求取和参数估计步骤为：

步骤1：计算滚珠丝杠副预紧力退化量增量：

Δxlij=xl,i,j+1-xl,i,j

(20)

步骤2：将每个应力水平下的滚珠丝杠副的预紧力退化量增量Δxlij(i=1,2,…,nl)分别按照升序排列，并用以下公式计算退化量增量对应的信度alijk：

(21)

(22)

(23)

其中，式(21)为期望估计公式，式(22)为中点估计公式，式(23)为中位秩估计公式。

步骤3：计算各应力水平数据权重：

不同的应力水平的性能退化试验数据在参数估计中的重要程度有所差异，因此，在进行参数估计时首先应计算数据权重。在对滚珠丝杠副副剩余寿命进行预测时，关注的是其随时间变化的规律，根据文献[16]，各应力水平的数据权重相同，即：

(24)

步骤4：建立最优化模型：

(25)

步骤5：将步骤2求得的信度、步骤3求得的数据权重以及预紧力退化量增量值代入式(25)并采用遗传算法进行最优化求解，求得最优解θi和最优值Qi(i=1,2,3)；

步骤6：比较Q1、Q2、Q3，取min{Q1，Q2，Q3}对应的最优解θi作为参数估计值。

3 预紧力加速退化试验

加速退化试验根据加载方式可分为恒定应力试验、步进应力试验和序进应力试验[13]。恒定应力试验是最早提出的加速寿命试验方法，也是发展最为成熟、最常用的一种试验方法。该方法首先选定若干加速应力水平S1、S2、…、Sn，并将一定数量的试验样件按照应力水平分组，每组样件在分配的应力水平下进行寿命试验，直至各应力水平下都有一定数量的样件失效或者达到一定的试验时间，其中，前者为恒定应力定数截尾加速退化试验，后者为恒定应力定时截尾加速退化试验。

3.1 试验装置

预紧力加速退化试验采用自主研发的滚珠丝杠副退化试验台和摩擦力矩测量试验台开展预紧力加速退化和检测试验。滚珠丝杠副退化试验台如图1所示，摩擦力矩测量试验台的如图2所示。其中，滚珠丝杠副退化试验台用于实现模拟滚珠丝杠副实际工作状况，其包括驱动伺服电机、阻尼器、轴向加载装置。通过控制驱动电机的转动方向实现滚珠丝杠副的往复运动，而阻尼器和轴向加载装置实现对滚珠丝杠副轴向加载，所加载荷的大小通过调节阻尼器中电磁线圈的电流大小来调节，而所施加力的大小可通过力传感器读出并实现反馈控制，保证施加载荷的稳定。摩擦力矩测量试验台用于实现空载状况下滚珠丝杠副摩擦力矩的测量，实现对滚珠丝杠副退化过程的监测，其包括定位装置(尾架、顶尖、三爪卡盘)、驱动装置(伺服电机)、摩擦力矩测量装置、测控系统等，其中，摩擦力矩通过压力传感器获得。

图1 退化试验台

图2 摩擦力矩测量试验台

3.2 试验方法

加速退化试验采用恒定应力加速试验方法，具体试验步骤为：

步骤1：选择试验滚珠丝杠副，按照要求在摩擦力矩测量试验台上测量滚珠丝杠副初始摩擦力矩，并换算为预紧力；

步骤2：将丝杠安装在退化试验台上，对其进行无负载跑和，检查试验台是否出现异常；

步骤3：启动退化试验台，开启冷降温装置，驱动伺服电机以恒定的速度进行试验，调节电涡流制动器至施加轴向载荷为设定载荷；

步骤4：一段时间后，拆下丝杠测量其摩擦力矩，换算为预紧力，判断是否超过预紧力失效阈值，若超过，停止试验，若未超过，重复步骤3直至超过失效阈值；

步骤5：统计实验数据，绘制预紧力退化曲线图。

滚珠丝杠副预紧力加速退化试验的流程图如图3所示。

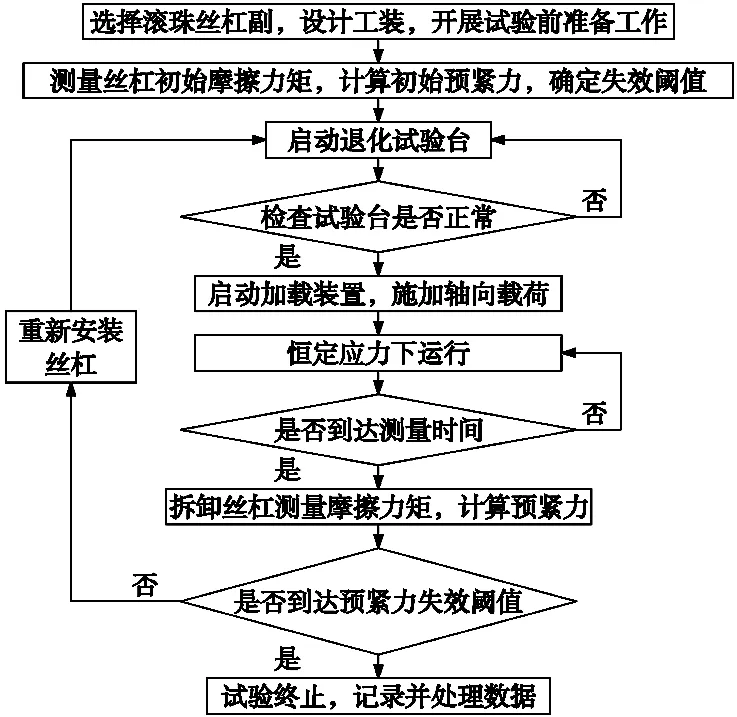
图3 加速退化试验流程图

实验室基于上述实验装置和试验方法对4组滚珠丝杠副(样件1～4)进行了预紧力加速退化实验[19]，本文将基于这4组数据对滚珠丝杠副预紧力退化寿命进行可靠性建模和可靠性分析。

4 滚珠丝杠副预紧力退化寿命可靠性分析

4.1 试验数据分析

将各样件的摩擦力矩换算为预紧力如图4所示。可以看出，样件的初始预紧力差距较大，其中样件2的初始预紧力最大，样件7的最小。其中，样本1的初始预紧力为6803 N，样本2的初始预紧力为8643 N，样本3的初始预紧力为7138 N，样本4的初始预紧力为7264 N。随着转数的增加，预紧力逐渐减小，且预紧力的变化存在两个不同的下降阶段，前一阶段预紧力减小的趋势较快，表示该阶段滚珠丝杠副预紧力退化较快，而后一阶段，由于滚珠丝杠副进入均匀磨损阶段，其退化趋于稳定，因此下降速率明显减小。

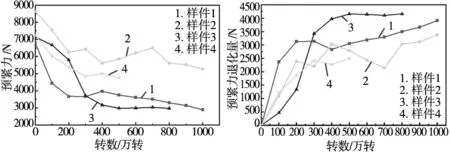
图4 滚珠丝杠副预紧力变化图 图5 滚珠丝杠副预紧力退化量变化图

根据式(7)计算得滚珠丝杠副的预紧力退化量变化图如图 5所示。

可以看出，随着转数增加，滚珠丝杠副的预紧力退化量总体上逐渐增加，且前一阶段增加较快，后一阶段增加较慢。从数据上看，样件1运行1000万转后预紧力退化3 908.14 N，样件2运行1000万转后预紧力退化3 372.23 N，样件3运行800万转后预紧力退化4 161.46 N，样件4运行500万转后预紧力退化2 490.72 N。

4.2 模型参数计算

根据文献[20]中基于维纳过程的性能退化模型，给出基于维纳过程的滚珠丝杠副预紧力退化的寿命可靠度函数为：

(26)

表1 维纳过程参数估计表

考虑到应力水平的范围及预紧力退化的趋势，本选用指数模型即式(6)计算应力加速因子s。需要说明的是，滚珠丝杠副在使用过程中，预紧力退化既受到外加载荷的影响，也受到预紧力本身的影响，因此，计算应力水平时应将同时考虑外加载荷和初始预紧力，计算出等效载荷作为滚珠丝杠副的应力水平[2]。常规工况下滚珠丝杠副的载荷一般不会超过额定动载荷的30%，因此，可以认为滚珠丝杠副的应力水平范围为0～30%Ca(Ca为额定动载荷)，通过计算，对于所给样件，其30%Ca在15 kN左右，为方便计算，取15 kN作为应力水平上限，因此，上限SU=15 kN，下限SL=0。代入式(6)计算得应力水平和应力加速因子如表2所示。

表2 应力加速因子表

根据式(21)～式(23)计算得所有退化量增量对应的信度均为0.5，根据式(24)计算得各应力水平的数据权重均为0.25。将信度和数据权重以及预紧力退化量增量代入式(25)，采用遗传算法求得各参数如表3所示。

表3 不确定理论参数估计表

4.3 滚珠丝杠副寿命可靠度模型分析

将表2中的参数值代入式(26)得基于维纳过程的滚珠丝杠副预紧力退化寿命的可靠度函数为：

(27)

对于滚珠丝杠副，根据文献[19]可知，当应力水平为预紧力的2.83倍时，滚珠丝杠副会发生卸载状态，即当预紧力退化到应力水平的1/2.83时，滚珠丝杠副将失效，因此，滚珠丝杠副预紧力退化量阈值为：

(28)

将表3中的参数代入式(19)并联立式(28)得基于不确定理论的滚珠丝杠副预紧力退化寿命的确信可靠度函数为：

(29)

基于上式建立的滚珠丝杠副维纳过程寿命可靠度模型和不确定理论寿命确信可靠度模型，对所给样件进行分析，首先计算这些样件的预紧力退化量阈值如表4所示。

表4 样件预紧力退化量阈值表

将表4中数据代入式(27)～式(29)分别求出样件1～4基于维纳过程的寿命可靠度函数及基于不确定理论的寿命确信可靠度函数，并进行仿真得到如下所示的仿真图。其中，图6为基于维纳过程和不确定理论的寿命可靠度仿真图。

从图6可以看出，随着寿命的增加，基于维纳过程的滚珠丝杠副寿命可靠度先保持1不变，再急剧下降，最后缓慢下降并趋于0，从数据中可以看出，预紧力退化量阈值越大，其寿命也越大。基于不确定理论的滚珠丝杠副寿命确信可靠度函数变化趋势与基于维纳过程类似，即先保持不变，接着急剧下降，最后缓慢下降。但是基于不确定理论的可靠度函数变化前期相对更为陡峭，后期更加平缓。

图6 寿命可靠度函数仿真图 图7 寿命可靠度模型三维仿真图

图7为假设初始预紧力一定时基于不确定理论的滚珠丝杠副寿命可靠度随寿命和应力水平变化的三维图。

从图7可以看出，当滚珠丝杠副的初始预紧力一定时，应力水平和寿命越大，其可靠度越小。当寿命较小时，应力水平对其可靠度影响较小，说明，在应力水平范围内，滚珠丝杠副可正常工作一段时间，随着寿命的增加，应力水平的影响逐渐增大，同一确信可靠度下寿命会随着应力水平的增大急剧减小。因此，滚珠丝杠副在使用过程中应保证其承受载荷在一定范围内，这样才能保证其寿命符合使用要求。

图 8为对应的等值线图。

图8 寿命可靠度模型等值线图

图8中粗实线为滚珠丝杠副确信可靠度为0.9时的等值线。从图中可以看出，寿命-应力曲线呈现反比例分布，与国标中寿命函数的变化趋势相同，即随着应力水平的增加，丝杠寿命先显著减小，后缓慢减小。

5 总结

本文基于不确定理论建立了考虑参数的认知不确定性的滚珠丝杠副预紧力加速退化试验模型，基于该模型提出了滚珠丝杠副寿命可靠度模型，通过与基于维纳过程的寿命可靠度模型对比，得出如下结论。

(1)基于维纳过程和基于不确定理论的滚珠丝杠副可靠度模型，其可靠度变化趋势都是随着寿命的增加，可靠度先保持不变，然后急剧下降，最后缓慢下降，但基于不确定理论的可靠性模型变化趋势前期更加陡峭，后期相对平缓。

(2)滚珠丝杠副的初始预紧力一定时，应力水平和寿命越大，其可靠度越小。当滚珠丝杠副的使用时间较短时，应力水平对其可靠度影响较小，但随着使用时间变长，在同一可靠度水平下，寿命会随着应力水平的增大急剧减小，因此，滚珠丝杠副在使用过程中应确保其载荷在应力水平许可范围内。