改进的交叉耦合控制策略在同步控制中的应用*
曹 原,贾 凯,徐 方,杜振军,刘明敏
(1.中国科学院沈阳自动化研究所机器人国家重点实验室,沈阳 110016;2.中国科学院机器人与智能制造创新研究院,沈阳 110169;3.中国科学院大学,北京 100049;4.沈阳新松机器人自动化股份有限公司,沈阳 110168)
0 引言
随着机器人技术的突飞猛进、智能化的提高,以多机器人协调进行的作业模式逐渐成为主流,同时机器人末端的位姿控制精度成为不可忽略的问题。机器人的同步控制技术在多关节单机器人系统中广泛存在,它通过一定的控制策略,有效的改善了机器人的跟踪精度,并在一定程度上提高了机器人的安全性和工作效率,为机器人的智能化发展奠定了基础。
在现有同步控制技术中,机械式同步方式由于机械结构长期运作导致的磨损以及装配误差等因素,影响整个系统的同步性能。随着数控技术的发展,电气式控制成为主流,分为非交叉耦合和交叉耦合控制策略[1-2]。非交叉耦合策略在整体上属于开环控制,同步控制性能较差[3-4]。为解决其开环问题,交叉耦合同步控制策略,实现了整体闭环效果[5];基于相邻两关节实际转速的相邻交叉耦合控制策略[6-9],控制结构相对简单,但并不适用于关节数目较多的情况;多关节的偏差交叉耦合控制结构[10]也被提出,但相对复杂计算量大。随着技术的进步,范志龙[11]在偏差耦合控制基础上,引入了表征所有关节速度的平均值作为评价函数;赵文兵等[12]提出了最大偏差耦合控制,将各关节速度极值作差得到最大偏差进行补偿控制;SHIH 等[2]提出的一种基于均值和极值的偏差耦合控制,有效改善了速度补偿器的不稳定性。谷雨等[13]在相邻交叉耦合控制策略的基础上,通过赋予电机不同权值,提出了加权交叉耦合的多电机同步控制策略与算法。
分析发现,现有交叉耦合同步控制策略对信号的跟踪情况存在两个问题。(1)以速度偏差作为的补偿只适用于输入信号相同的前提下;(2)以各关节间的跟踪误差差值进行变换得到的补偿计算量大,没有考虑跟踪误差极值对整体系统的影响,鲁棒性差。针对以上问题,本文设计了改进型交叉耦合同步控制策略,以各关节跟踪误差差值经过加权变换,并将极值和平均值耦合作为同步误差,其次分析了策略原理,进行了稳定性判定,最后通过对比实验,对其控制性能、鲁棒性进行了对比分析。
1 改进的交叉耦合控制策略
本节分别介绍了文章涉及到的同步控制思想与改进的同步控制策略,其中着重介绍了所提出的改进型交叉耦合控制策略依据及具体表现形式。
1.1 同步控制思想
对于多关节系统的同步控制主要包含两个方面:跟踪误差和同步误差。
在多关节系统的同步控制中,设第i关节的跟踪误差表征如式(1)所示。
(1)

为达到各关节的同步控制,当某一关节的跟踪误差ei(t)趋于0时,应满足各关节的跟踪误差都等于0。
1.2 改进的同步控制策略
不考虑关节摩擦力以及外部扰动,对于n关节的机器人系统模型[15]可以由式(2)表示。

(2)

n个关节的跟踪误差分别表示为:
(3)
对于第1.1节提到的同步控制思想,在系统中,不仅要考虑单个关节的跟踪误差,同时考虑其他关节的影响。当其中一个关节受到扰动脱离期望值时,系统中的其他关节都会受到影响并且通过调节转速来抵消扰动。设两关节i、j之间的同步误差为εij(t),如式(4)所示。
εij(t)=ei(t)-ej(t)
(4)
当考虑到所有关节所受影响时,此时第i关节的同步误差表示如式(5)所示。
εi(t)=λi1(ei(t)-e1(t))+λi2(ei(t)-e2(t))+…+
λi1e1(t)-λi2e2(t)-…-λinen(t)
(5)
对于n关节系统,可将(5)式表示为矩阵形式,如(6)式所示。
(6)
定义:
(7)
为解决第1节提到的极值对整体系统影响大的问题,现将所有关节跟踪误差的极值和平均值也耦合到同步误差其中,则(6)式更新表达式如下:
(8)
式中,
(9)
此时,
(10)
则矩阵可变化为下列形式:
ε(t)=RE(t)
(11)
式中,ε(t)为多关节系统的同步误差矩阵;R为系统的关系矩阵;E为系统的角速度跟踪误差矩阵。
如图1所示为关节1的同步误差结构图,第一关节的同步误差分别包含了关节1误差与其他关节的差值,并根据各关节的影响度赋予对应的权值,同时,通过比较得到所有关节误差的极值以及平均值,经过变换耦合到其中,具体结构如图所示。其它关节依次类推。

图1 改进的同步控制策略关节1同步误差结构示意图
当系统满足e1(t)=e2(t)=…=en(t)→0时,同步误差ε(t)→0,可以达到系统的同步控制。
1.3 控制器设计
为提高多关节系统的同步控制性能,有效的控制多关节系统,关键应考虑控制关节的跟踪误差和同步误差[17]。多关节系统的总误差表达式如式(12)所示。
(12)
式中,∂i为正常数。
因此,设计控制函数ui(t)如式(13)所示。
(13)
式中,ci为正常数,由式(13)定义以下向量。
(14)

(15)

通过对式(2)、式(14)、式(15)联合处理,得到对于n关节的机器人系统的闭环控制方程:
(16)
1.4 系统稳定性及有效性分析
在得到系统的闭环控制方程后,验证系统是否具有稳定性,这里采用Lyapunov进行稳定性判定。首先选取Lyapunov函数如下:
(17)
式中,Mi、kε、ci、∂i、kε、λij等系数都为正常数,其它项为平方项,观察可得V(t)≥0,满足正定条件。现对函数求导如下:
(18)
通过式(16)与式(18)可得:

(19)


系统关系矩阵R为对阵矩阵,因此R′Ti=Ri,式(20)可变换为:
(21)
式中,
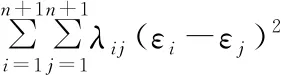

将式(20)~式(23)联立后代入式(19),最终化简得到如下表达式:
(24)
2 仿真与实验
2.1 实验设置
本节分别搭建了最大偏差耦合控制策略、加权耦合型同步控制策略以及本文改进的交叉耦合控制策略的Simulink控制框图,文章实验采用控制变量原则进行实验对比,文章分别进行两组对比实验:相同输入信号下,不同控制策略的对比;不同输入信号下,不同控制策略的对比;为达到明显实验效果,两组实验都分别在干扰有无的情况下进行对比分析。
在对比实验中,每种策略都应用在三个关节的控制系统中,每个关节均采用孙怡[14]推导的电机数学模型,具体模型如式(25)所示;为保证变量统一,每个关节采用传统的PID控制,并且对PID参数的设置统一为Kp=20、KI=1250、KD=0.000 1;当控制策略面对不同输入时,阶跃信号0.5 s时刻突变,突变时刻跟踪误差较大,相对于其他关节来说是干扰,此时对整个系统的影响较大。为保证实验的准确性,在多关节同步控制仿真实验中要加入干扰来验证同步控制策略的性能。下面将通过三组实验,详细对比三种控制策略。
(25)
2.2 最大偏差耦合控制策略
最大偏差耦合控制主要思路是对各关节实际角速度信息进行对比,得到极值偏差,并利用极值偏差进行补偿。
根据图2结构示意图,利用MATLAB的Simulink模块进行建模分析。
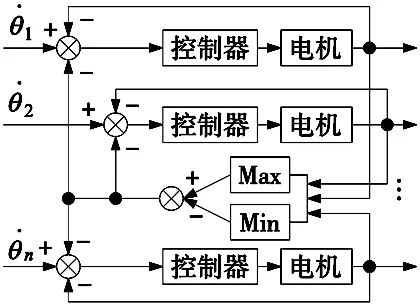
图2 最大偏差耦合控制结构示意图
如图3所示,图中共包括3条支路,每条支路的输入信号都是正弦信号,当进行不同信号输入实验时(不同信号的输入模型在文章内未给出),需要把Sine Wave02和Sine Wave03两支路信号分别更改为余弦信号和阶跃信号即可,其它量全部保持不变。

图3 最大偏差耦合控制策略Simulink建模
2.3 加权耦合型同步控制策略
赵文兵[12]提出的加权耦合型同步控制策略的同步误差表达式如式(26)所示,建立的Simulink控制框图如图4所示。

图4 加权耦合型控制策略Simulink建模
(26)
2.4 改进的交叉耦合控制策略
对于本文提出的改进的交叉耦合控制策略,根据图1同步误差结构示意图,建立图5所示的控制系统,控制策略考虑了所有关节跟踪误差的极值和平均值。在加权耦合型同步控制系统和改进的交叉耦合型控制系统中,增益Gain1-6统一分别设置为1、0.1、1、0.1、1、1,同步误差系数设置为1。在进行干扰实验时,统一设置在第3关节加入时间1 s~1.01 s的阶跃干扰信号,具体控制框图文章不再给出。

图5 改进的交叉耦合控制策略Simulink建模
3 实验结果与分析
本节对不同控制策略在输入信号相同和不同的两种情况下的结果进行了对比分析。后文中将以控制策略Ⅰ代表最大偏差耦合控制策略、Ⅱ代表加权耦合型控制策略、Ⅲ代表改进的交叉耦合控制策略。
3.1 输入信号相同的实验结果
首先是相同信号输入下无干扰的分析图,3种控制策略的输出结果及误差分析图基本一致,图6只给出了控制策略Ⅰ的分析图。输出结果大致相同,表明了3种控制策略都适用于输入信号相同且无干扰前提下;结果大致相同的原因在于系统无干扰、3关节模型都相同、除了控制策略不一样其他条件都一样,实验条件较为理想,现实中可能会存在干扰、模型不同等因素。理想条件下,3关节输出都相等,关节间的耦合误差都为0,因此造成了结果大致相同。对于此,文章在第3关节加入干扰进行模拟试验后,得到如图7所示分析图。

(a) 控制策略Ⅰ输出图 (b) 控制策略Ⅰ误差分析图

(a) 控制策略Ⅰ输出图 (b) 控制策略Ⅱ输出图
由输出图可以观察到,第3关节碰到干扰时,第1、第2关节也会根据第3关节的误差做出相应的调整,调整后都会继续跟随原信号输出;对比3个策略的误差图,在输入信号相同且存在干扰前提下,本文提出的改进的交叉耦合控制策略同步控制性能略优,误差最小,第3关节误差数值达到0.045 79。
3.2 输入信号不同的实验结果
本小节将在输入信号不同前提下,进行有干扰和无干扰的两种实验对比分析。对于整个多关节控制系统,3个关节信号依次为正弦、余弦和阶跃信号。无干扰情况下的3种控制策略仿真结果如图8所示。
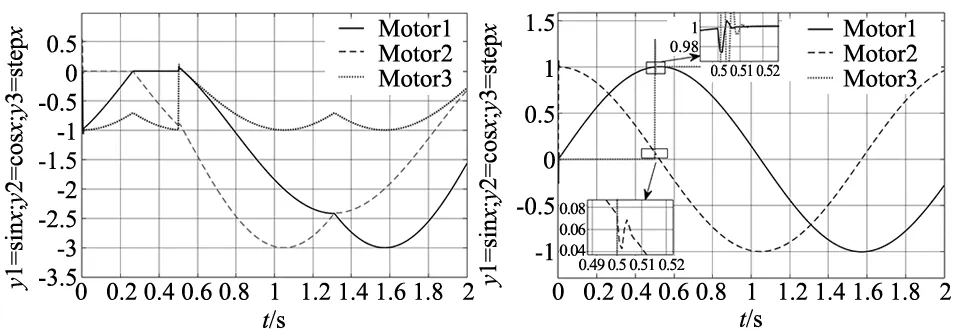
(a) 控制策略Ⅰ输出图 (b) 控制策略Ⅱ输出图
系统在1 s~1.01 s有阶跃信号干扰的情况下进行仿真实验,得到如图9所示的干扰仿真结果对比图。

(a) 控制策略Ⅰ输出图 (b) 控制策略Ⅱ输出图
3.3 结果分析
如表1所示,对以上4组实验:相同信号下无干扰仿真、相同信号下有干扰仿真、不同信号下无干扰仿真以及不同信号下有干扰仿真的结果进行了分析汇总。由于实验中是在第3关节加入的干扰,因此在分析中,主要包括了第3关节的最大跟踪误差,以及各关节稳定后的稳定误差。

表1 各控制策略仿真结果分析表
在相同信号无干扰情况下,数值一致,第3.1节已详细说明原因;在相同信号有干扰情况下,从第3关节最大跟踪误差可以得出,控制策略Ⅲ误差为0.048 03,优于控制策略Ⅰ、Ⅱ,控制性能较好;另外,根据相同信号下的实验数据可以得出,三种控制都适用于输入信号相同的情况。
对比控制策略Ⅰ的4组实验,在不同信号下,各关节误差不收敛,结果毫无意义,因此以实际输出作为补偿的最大偏差耦合控制策略根本不适用于不同输入情况下;而控制策略Ⅱ、Ⅲ的误差基本收敛,首先证明了加权耦合型控制策略以及本文提出的改进的交叉耦合控制策略适用于输入信号不同的情况下;另外,从表中可以得到,在不同信号下有干扰和无干扰下时,控制策略Ⅲ的误差普遍小于控制策略Ⅱ。
综上所述,通过以上的控制变量对比实验,本文提出的改进的交叉耦合同步控制策略既适用于输入信号相同情况,同样也适用于输入信号不同前提下;另外通过有无干扰对比实验,证明了将极值和平均值耦合到误差中,有效的解决了误差极值对整体系统影响大、鲁棒性差的问题,本文提出的改进的交叉耦合同步控制策略在面对干扰时,控制性能较为优越。
4 结语
文章分析了现有同步控制策略的优缺点,针对总结提出的现有策略存在的问题,本文提出了改进的交叉耦合同步控制策略,分析了策略原理,并通过李雅普诺夫定理进行了稳定性判定;最后通过MATLAB/Simulink搭建了最大偏差耦合控制策略、加权耦合型控制策略以及本文提出的改进的交叉耦合控制策略控制框图,通过控制变量法,分别对3种策略进行了以输入信号是否相同、有无干扰为前提的4组对比实验。结果表明:本文提出的改进的交叉耦合同步控制策略适有效的解决了误差极值对整体系统影响大的问题,控制性能更为优越,鲁棒性高,在多关节机器人的同步控制领域中具有较大的参考性和实用性。

