基于NSGA-Ⅲ的多目标柔性车间调度

李鹏，徐龙艳，雷俊松，吕勇，毕亚球

（1.湖北汽车工业学院 电气与信息工程学院，湖北 十堰 442002；2.十堰市计量检定测试所，湖北 十堰 442000；3.湖北汉唐智能科技股份有限公司，湖北 十堰 442000）

在实现“双碳”目标的要求下，国家对制造业节能减排提出了新的要求［1-3］。尽管企业对制造技术进行更新升级，但仍存在资源浪费［4-5］。数据表明，制造过程中非切削工序消耗了95%的时间，有效的柔性作业车间调度方法对提高企业生产力具有重要作用［6］。针对多目标柔性作业车间调度问题，尹爱军等［7］研究了遗传退火算法，针对最大化生产时间、最小化生产成本和最大化客户满意度采用融合海明相似度的改进算法优化多个目标；张丽等［8］针对最大化完工时间和能耗提出融合密度估计方法的改进NSGA-Ⅱ算法；裴小兵等［9］以最小化完工时间、总机器负荷最小和临界机器负荷最小为目标，提出了基于三方博弈的改进遗传算法求解多目标柔性作业车间调度模型；Tao 等［10］针对低碳排放约束的柔性作业车间调度问题，提出了基于双链编码的改进量子遗传算法，并且在选定模型的基础上，提出了使用改进的双链量子遗传算法求解加工路径选择的方法；林震等［11］构建了以加工成本、瓶颈机器负荷、机器总负荷及制造工期为目标函数的柔性作业车间调度多目标优化模型，提出了融合多交叉策略的多目标遗传算法，通过2个基准实例求解对比分析表明所提方法的有效性；解潇晗等［12］分析了工艺车间调度中能量消耗的重要环节和特点，以能耗和生产时间为优化目标建立数学模型，采用多层编码，对能耗和生产时间进行加权求和处理，采用多目标优化算法实现调度策略。但上述研究在求解多个优化目标时多个影响因子相互制约，对于高维多目标优化问题，NSGA-Ⅱ会面临如基于Pareto支配关系所导致的选择压力过小、拥挤距离在高维空间不适用造成计算复杂度过高等问题。文中以最小加工时间、成本、质量和能耗为优化目标构建数学模型，运用改进NSGA-Ⅲ算法对多目标柔性作业车间调度问题进行求解。

1 问题描述

柔性作业车间调度是指n（i1，i2，…，in）个工件在m（j=1，2，…，M）个机器上加工，工件的每一道工序均可在任意满足加工要求的机器上完成。生产调度是指在满足每个工件生产工序的基础上，为工序安排合适的加工机器，同时实现给定的优化目标。结合实际生产情况，根据FJSP模型要求，进行以下假设：1）柔性作业车间调度过程不能被中断或抢断；2）加工同一个工件时需按照工件工序依次加工；3）在同一时刻，1道工序最多只能被1台机器加工；4）所有机器和操作在零点时同时可用；5）同一时刻1台机器最多只能加工1道工序；6）所有的参数均为正数：7）工件之间的转运时间、成本和能耗不予考虑。优化目标函数为

式中：下标max、avg 和min 分别表示Pareto 解集中对应参数的最大值、平均值和最小值。

2 改进NSGA-Ⅲ算法

与NSGA-Ⅱ相比，NSGA-Ⅲ通过广泛引入参考点，在解决多目标优化问题时其收敛性得到明显的改善［15］，但是无法保证超平面上的参考点均匀分布，间接导致算法早熟，使其搜索能力下降，因此需要对算法进行改进。

2.1 编码与解码

如图1所示，文中采取小数编码。假设机器数为18，工件数为6，工序数为18，编码分上下2 段，分别为工序号和机器号。由于两段编码的范围不同，因此采取0～1之间的随机数表示加工顺序和加工机器。工序编码时，首先将所有加工顺序以向量的形式表示，数字为工件号，出现的次数为工序。将编码得到的小数由小到大进行排序，与排序前的编码进行对比，将编码与工序一一对应，根据数字的变化情况产生不同的工序方案。机器解码时，为了使工序与机器对应，保证加工机器可用，在解码时候转换为对应的整数，进而实现实际机器的安排。图1中，第1个机器编码为0.8620，其对应的工件2工序1，通过机器矩阵查询，可以加工工序1的机器有1号、3号、4号和6号4个机器，对编码与机器数的乘积执行向上取整规则得到4，因此确定加工该工序的机器为6号机器。

图1 解码图

2.2 种群初始化及自适应交叉变异

采用随机搜索策略和贪婪有序策略生成初始种群，2 种策略初始种群个体数量比为7∶3。种群交叉和变异的过程中，交叉和变异概率的大小影响算法的性能［16］。在基本NSGA-Ⅲ算法中，交叉概率pc0和变异概率pm0为固定值，为使算法避免过度发散和陷入局部最优提出自适应交叉变异概率：

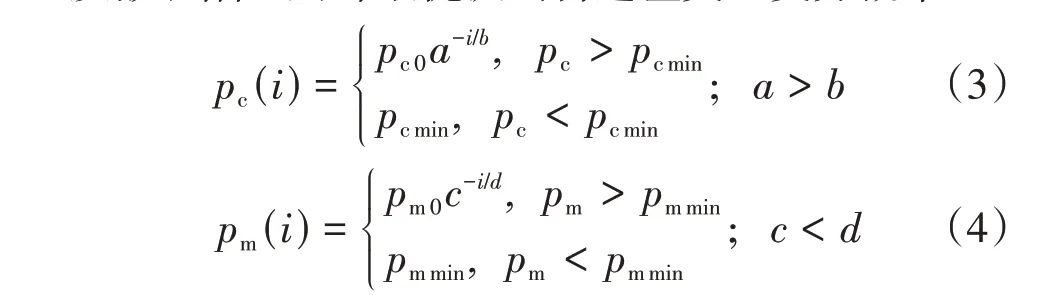
式中：pcmin和pmmin分别为最小交叉和变异概率；a、b、c、d均为控制参数；i为进化次数。

2.3 基于目标空间参考点选择策略

1）净化目标空间 父代个体经过基因重组后，得到新的种群S，对其进行最值归一化操作：定义S的理想点为Fi（x）的最小值zimin，进行目标函数的转化：

2）确定参考点 NSGA-Ⅲ预定义了参考点以保证最优解的多样性，参考点定义在维度为M的超平面上，将超平面分为p等份后得到参考点：

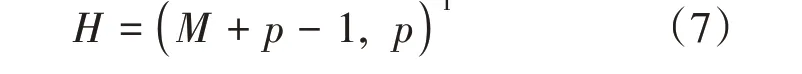
3）关联个体和参考点 随着迭代的进行，参考点分布在解空间中，以原点和参考点为基准确定参考向量，计算个体与参考向量的截距，截距最小的个体互相构成关联参考点。若产生关联参考点，则说明所得解在解空间中分布广泛，也说明了这些解达到了全局最优的效果。

4）交叉操作 假设共有F层个体，将产生的新个体分配至第St层，从F1到FL层中的个体数目首次大于N或者（St+1）层的个体大于目标数，则需要对（St+1）层的个体进行筛选。筛选时，遍历每个参考点，将数量最少的参考点Pj进行归属，若无归属参考点，则Pj值为0。若最后一层非支配层FL有归属的参考点个体，则从中选取距离最小的点加入到下一代种群中，采取欧氏距离判断参考点的关联度，此时Pj的值增1 个单位；若最后一层无归属参考点，则淘汰该参考点。

3 仿真分析

改进NSGA-Ⅲ（简称R-NSGA-Ⅲ）采用MATLAB R2019b 编程，种群规模设置为30，交叉和变异中的参数a、b、c和d分别取值0.1、0.1、0.9和0.7。mk01～mk05 为不同工件和工序的标准数据集，将R-NSGA-Ⅲ与NSGA-Ⅲ、PSO 和SAA 在5 种不同测试数据测试后得到平均加工时间、成本、质量和能耗，结果见表1。对比发现，R-NSGA-Ⅲ在加工时间、成本和能耗方面略低于其他3 种算法，在加工质量方面，R-NSGA-Ⅲ高于NSGA-Ⅲ和SAA。

表1 算法独立运行200次Pareto解集数和运行时间对比表

以mk01为实例仿真，算法独立运行200次，图2 为得到非支配解和对目标函数采用最值归一化操作后的对比图，线条数量代表所得非支配解的数量，转折点为算法对应不同优化目标的计算值。通过对比可看出R-NSGA-Ⅲ获得Pareto 解的数量优于其他算法，且R-NSGA-Ⅲ在加工时间、成本、质量和能耗方面优于其他算法，说明R-NSGA-Ⅲ算法得到的Pareto解集具有良好的收敛性和多样性。对结果进行排序可以得到最优调度方案的甘特图。以mk01数据集为例，在运行R-NSGA-Ⅲ算法后得到最佳调度方案，如图3 所示，其中不同的颜色和数字分别代表不同的工件和工序。101 表示工件1的第1道工序在设备6上加工，以此类推，从图中可以看出最大加工时间为58 s。从以上实验结果中可以看出R-NSGA-Ⅲ算法的求解质量和成功率都高于其他算法。

图2 不同算法下非劣解和目标归一化结果对比图

图3 基于mk01的R-NSGA-III最佳调度方案图

4 结论

针对多个优化目标，提出了改进NSGA-Ⅲ算法。算法设计了一种基于小数的双层编码方式，且引入自适应交叉变异策略，避免种群在交叉变异过程中产生无效解。针对NSGA-Ⅲ算法超平面上的参考点分布不均匀的问题，提出基于目标空间参考点选择策略。通过仿真实验分析，验证了算法的可行性和有效性。