面向细纱机性能退化的可靠性评估模型*

赵 放

(西安工程大学 科技处，西安 710048)

细纱机作为一种典型的大型复杂机电一体化设备，其内部结构复杂、关键器材专件繁多。以一台1 200锭的细纱机为例，其涉及60多个关键器材专件、107 029个零件和100多个传感器。作为纺织厂成纱质量的最关键设备，其性能优劣直接决定着纺纱成品以及后序织物的品质。

在整个纺纱过程中，细纱机长期处于连续、不间断，而且高温、高湿、强电的工作环境中，其锭子、传感器、电机等关键器材专件因受潮湿、磨损、疲劳、震动等因素的影响，导致细纱机的性能加速退化。另外纺纱过程工况多变、品种翻改频繁、器材专件维修滞后等人为因素的影响，更加剧了细纱机的性能退化。因此，如何对细纱机性能指标的退化过程进行可靠性评估是一个亟待解决的课题[1]。

对细纱机性能退化可靠性评估的现有研究，国外学者早期的研究焦点在细纱机的组成结构、牵伸机构齿轮磨损等方面。文献[2]分别在I型、II型截尾试验下给出了威布尔分布模型极大似然估计，并对细纱机牵伸机构性能进行了评估，文献[3]在I型截尾试验下讨论了逆威布尔分布的统计分析问题，探讨了细纱机组成机构的可靠性。后来，随着理论研究的不断深入、研究涉及的变量也越来越复杂，研究的焦点主要集中在细纱机性能可靠性分布、可靠性指标构建、故障频率预测等方面。文献[4]将日常改善的理念应用于环锭细纱机整体性能提升方面，并借助帕累托分析、原因逻辑分析和因果分析，检查了六大停工损失，即故障或设备故障、设置和调整、空转和小停工、速度降低、过程缺陷和产量降低，结果表明细纱机的性能从75.09%提高到86.02%，生产率提高了23.93%，不良品的产量降低了49.50%；文献[5]针对环锭纺纱机故障问题，提出了一种基于预测分析的正则化深度神经网络的预测维护和体系结构，结果表明该体系在通过为每个部件提供基于状态的监测来预测异常、干扰和故障，从而在操作过程中通过神经传感网络使用智能代理更准确地定位当前纺纱锭子中定义的部件故障，但问题是尚未考虑锭子的性能指标退化问题，以及部件故障对成纱质量的影响；文献[6]针对细纱机性能退化问题，基于教学优化算法，确定了环锭细纱机前后区变量和转杯纺纱过程输入变量的最佳参数组合，结果表明这种参数组合可以有效地应用于细纱机性能退化过程，并获得不同输入变量的最佳组合，从而实现目标质量特性。除此之外，还有学者探讨了细纱机性能退化的建模问题。文献[7]研究了一种基于蒙特卡罗的细纱机系统故障仿真模型，对细纱机的性能参数进行了预测，但未对细纱机性能指标的退化过程进行预测，文献[8]利用Wiener 模型描述了细纱机的性能退化过程，并对细纱机的剩余寿命分布进行了函数解析，等等。

在我国，学者们对细纱机性能可靠性评估的研究，早期的研究焦点主要集中在细纱机的内部结构、器材专件、牵伸机构磨损等方面。文献[9]应用二维Birnbaum-Saunders分布构建细纱机器材专件失效机理间的相依关系，并在自适应逐步混合截尾恒加寿命试验下获得了未知参数的极大似然估计和区间估计，并对试验过程中移走的未失效产品的竞争失效时间进行预测；文献[10]采用二维Birnbaum-Saunders分布描述细纱机器材专件失效机理间的相依关系，基于恒加寿命试验数据，给出参数的极大似然估计和区间估计，并针对失效机理之间的独立性以及多个失效机理间的形状和尺度参数之间关系进行了检验。后来，随着研究方案的不断深化，研究涉及的关系也变得复杂，研究焦点主要集中在细纱机罗拉故障识别诊断、细纱机故障时间、模式、原因及修复时间等方面[11]。文献[12]提出了融合长短时记忆网络和深度置信网络的指标构建方法，并利用构建的退化指标与传统的单一退化表征参数进行对比，结果表明在一定程度上其能够更好的体现设备的退化过程；文献[13]研发了一种面向细纱机的光电反射式故障诊断器，并将其应用于细纱机钢丝圈的运动轨迹，较好地解决了细纱机对成纱断头的影响问题，以及文献[14]提出了一种面向细纱机的罗拉故障特征信息提取方法，通过该方法的实际应用，较好地解决了细纱机的罗拉故障混频问题。

国内外学者们对细纱机性能可靠性评估的研究，主要从失效时间、设备内部故障等角度入手，利用单一表征参数来表征细纱机的性能退化轨迹，目前已经解决了细纱机故障时间、故障时间、模式等问题，但还存在细纱机性能退化过程的可靠性评估问题尚未彻底解决。

文中利用Weibull分布对细纱机的性能突发失效过程进行了预测，并利用Copula函数构建了一种面向细纱机性能退化的相依竞争失效模型，以实现细纱机性能指标退化过程的评估。

1 细纱机性能退化参数

按照纺纱工艺原理，从细纱机自身、电气系统两方面入手，选择细纱机运行过程中的性能参数、工艺参数，将其作为细纱机性能退化的性能参数。

细纱机的性能退化过程具有多种退化过程的特点，而且退化失效机理相对复杂，这给退化模型的精准建立带来了挑战。因为细纱机在连续不间断工作环境下其性能指标发生性能退化，导致实际性能指标与给定的工艺指标之间发生偏差，而重复计算细纱机故障模式、失效机理和退化指标耗时非常大。为此，根据细纱机的历史性能参数、工艺参数，以及相互之间关系来描述细纱机性能指标的退化过程，以实现对某个性能参数随时间变化的退化过程的评估。然后，在细纱机性能退化建模过程中，需引入一些典型的评价指标来评价其性能的退化过程。

2 细纱机性能退化过程建模

细纱机作为一种大型机电设备，其性能退化失效过程是一个由多个性能参数共同作用的结果，仅单一参数标准不能很好的表征细纱机的性能退化。为此，考虑到不同性能指标之间存在信息重复的现象，以及细纱机性能随着时间推移致使其需要表征的指标越来越多，为此，需要建立一个科学合理的性能退化模型来表征性能退化过程，具体的构建过程如下。

2.1 性能退化参数筛选

根据可靠性理论[9]，其为产品性能失效机理的探究奠定了基础，而且从零件、部件和系统等产品的可靠性方面的数据进行收集与分析做起，对失效机理进行了系统研究，这为细纱机性能退化指标的选择提供了理论基础。因为：在可靠性理论中，通过敏感度、相关度、重要度等一系列评估标准，对产品进行可靠性设计、可靠性制造，以及保证产品的可靠性。而且，敏感度主要反映的是产值在整个设计、制造过程中其性能指标的变化幅度或变化情形，相关度主要反映的是产品性能指标之间的相关程度，而重要度主要反映的是产品性能指标变化去其他指标的影响程度。

由此，在探讨细纱机故障模式、失效机理和退化指标基础上，引入敏感度、相关度、重要度三个评估标准，从而筛选出性能更优的细纱机性能退化参数。

2.1.1 敏感度

现假设细纱机历史性能监测数据包括N个样本点，性能退化参数为M维，则细纱机在监测时间ti的监测值Xi由M维性能监测参数构成，而且每一维性能参数都是长度为N的序列。同时，将参数变化幅度作为性能变化的参数标准，并将其进行标准化[15]。

定义细纱机台数为n，第j个参数的变化幅度为cj，即敏感度，在失效监测范围内的最大值、最小值分别为maxc,j和最小值minc,i。

(1)

2.1.2 相关度

(2)

2.1.3 重要度

利用序关系分析法[16]，利用式(3)对细纱机性能退化的特征参数yi(i=1，…，n)进行重要度的比较。在式(3)的基础上，对特征参数的重要度排序。第j个特征参数的重要度pj可以表示为

(3)

(4)

在三个标准的基础上，利用主成分分析在高维数据降维方面的优势，将细纱机的多性能退化指标重新组合，使其成为低维、相异的主成分指标，这为细纱机性能退化的表征带来了便利条件。

当细纱机的退化严重时，退化部位在牵伸过程中不能正确地控制成纱纤维，导致成纱质量下降，这意味着细纱机性能指标优劣直接作用于成纱质量，由此可将整个细纱机性能退化过程视为一种以在制品为载体的质量损失的传递和相互交集的过程，这意味着评估细纱机性能退化的三个标准之间是一种交集关系。从根本上讲，仅单一的标准往往不能准确衡量细纱性能指标的退化过程。为此，借助灰色关联分析方法在综合表征多因素之间关联关系方面的优势，将敏感度、相关度、重要度三个标准进行综合考虑，使其转为一种综合判断标准，并利用相互之间的交集关系更客观地评估细纱机性能指标的退化过程。

在细纱机的实际生产过程中，各个评估标准之间的重要程度也存在差异性，并不能很好的表征各个性能指标之间的重要性。因此，为消除各个评估指标之间的差异性，借助CRITIC法在目标赋权方面的优势，对三个判断标准采用累积方法进行综合赋权。

① 数据归一化处理

由于各个标准评估所需细纱机性能指标数据具有统一性，同时为消除各标准之间的差异性，需要对其所用的细纱机性能指标数据进行归一化处理，具体处理过程为

(5)

式中：yij为细纱机性能指标处理后的第i行第j列数值;yijmin为性能指标的最小信噪比;yijmax为性能指标的最大信噪比;xij为yij处理后的数值。

② 确定灰色关联系数

在重要度定义的基础上，根据灰色关联分析方法，将细纱机性能指标数值规范化处理后的数据与参考序列的关系定义为灰色关联系数[8]，其具体计算过程为

(6)

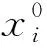
③ 赋权重

赋权重(Criteria Importance Through Intercrieria Correlation，CRITIC)法作为一种客观赋权法，通过对比强度和指标间冲突性来衡量所反映的信息量的大小。其中，对比强度通过标准差方式体现，指标间冲突性通过相关系数来体现。

基于归一化处理后的细纱机性能指标，根据CRITIC赋权重方法，采用累积方式对敏感cj、相关度sj、参数重要度pj三个判断标准进行综合赋权，得到综合筛选参数标准hj为

hj=cj*sj*pj。

(7)

2.2 性能退化指标建立

对细纱机无论是由外部作用导致的突发失效，还是由自身性能退化导致的失效，都会直接作用于成纱质量。为此，还需对细纱机的状态特征数据进行归一化处理。

2.3 性能退化模型构建

Wiener 过程能够描述非单调的退化过程[17]，为细纱机性能退化建模带来了便利。为此，利用Wiener过程构建细纱机性能退化模型：

Y(t)=Y(0)+μt+σB(t)。

(8)

式中:Y(0)为初始时刻的综合性能退化量；μ为飘移系数；B(t)为标准布朗运动；σ为扩散系数。

假设细纱机性能失效阈值为ω，寿命为T，则通过式(8)，细纱机的寿命可定义为

T={t:Y(t)≥ω|y(0)<ω}。

(9)

由式(9)可见，细纱机的寿命服从逆高斯分布，进而寿命T的概率密度函数和可靠度函数可分别表示为

(10)

(11)

其中Φ(·)为标准正态分布函数。

2.4 性能突发失效过程预测

通过式(10)、式(11)，可以对未知参数μ和σ2进行计算，并得到相应地估计值。在此基础上，通过构建的性能退化模型，对细纱机突发失效过程进行预测。而威布尔分布(Weibull分布)在拟合不同类型的分布时具有良好的适应性[18]，这为预测提供了便利。为此，将细纱机t时刻退化量为x对应的突发失效故障概率为λc(t|x)，则根据威布尔分布建立如下关系式：

(12)

通过式(12)，突发失效时间Tc的概率密度函数和累积分布函数为

(13)

Fc(t|x)=P(t>Tc|x)

(14)

由此，细纱机在t时刻性能突发失效的可靠度[19]Rc(t|x)可以表示为

(15)

2.5 竞争失效模型构建

细纱机性能指标的退化失效过程往往受到温湿度、原材料、系统及人为等多因素的交叉影响，使得某些性能指标的退化过程之间具有一定的相关关系。 利用式(10)对整个细纱机性能指标的退化失效过程进行分析，易导致可靠度函数的误差较大。为此，还需要开展多性能指标之间的相关性分析。

当细纱机的性能突发失效与退化失效之间不存在任何关系时，可将这两种过程简单的串联，可靠度Ri可表示为

Ri=Rw(t)Rc(t)。

(16)

在工作实际中，细纱机性能突发失效与退化失效之间存在一定的关联性。为此，借助Copula函数在处理相关性问题方面的优势，构建了一种基于Copula函数的细纱机性能相依竞争失效模型[20]，实现不同过程之间的相关性表征。

设fY(t)为细纱机综合性能退化量Y(t)的密度函数，fTc(t)为突发性失效时间Tc(x)的密度函数，则{Y(t),Tcx}的联合分布函数为

H(Y(t),Tc(x),θ)=C(FY(t),FT(t),θ)。

(17)

同时，{Y(t),Tc(x)}的联合密度函数为

h(x,t,θ)=c[FY(t),FT(t),θ]fY(t)fTc(t)。

(18)

根据AIC 准则、Gumbel Copula函数，选择最优的函数进行细纱机性能突发失效与退化失效的相关性分析，具体过程为

由此，根据Kendall的τ与Gumbel Copula函数之间的相关关系，可以得知τ=1-θ-1，即所谓当θ=1时，各个随机变量之间是一种独立关系。在此基础上，根据文献[13]的结论，选取Gumbel Copula函数来构建细纱机性能指标退化的竞争失效模型。

假设1在应力水平Si,i=1,2,…,u下，通过Gumbel Copula函数来表征细纱机性能指标之间的相依关系，则与之对应的可靠度函数为

由此，在应力水平Si,i=1,2,…,u下，细纱机性能指标退化且失效时间小于给定时间t的概率为

细纱机性能指标退化密度函数表示为

同理，细纱机性能指标退化且失效时间小于给定时间t的概率、不完全密度函数可分别表示为

3 参数估计

假设性能指标在初始时刻t0的退化量Y0=0，则ΔYi=Yi-Yi-1为细纱机在时刻ti-1和ti的退化增量，Δti=ti-ti-1为时刻ti-1和ti的时间间隔，则由Wiener随机过程的性质可得ΔYi～N(μΔti,σ2Δti)。由此，基于Wiener随机过程的细纱机性能退化模型参数的似然函数为

(19)

在式(19)的基础上，对μ和σ2进行求偏导计算，令偏导为零，则可以对方程进行求解得到μ和σ2的估计值分别为

(20)

(21)

结合式(20)、式(21)，可得到细纱机性能退化过程中的寿命密度函数和可靠度。

记录n台细纱机在性能突发失效时间(Tc1,Tc2,…,TcN)对应的性能退化量为(x1,x2,…,xN)，则根据式(14)可以得到似然函数为

(22)

目前，基于Copula函数的参数估计相对较多，但大部分计算过程复杂，再加之细纱机性能退化模型复杂，未知参数较多等问题，使得常见的参数估计方法不适合细纱机性能的参数估计。而基于贝叶斯理论的Gibbs算法为该参数估计提供了可能。

由此，利用Gibbs抽样算法获取细纱机性能参数的贝叶斯估计，其中参数α,λ和βj,j=1,2,…,k的最大后验密度可信区间可由以下步骤获得。

② 参数α,λ和βj,j=1,2，…，k的可信水平为100(1-γ)%的贝叶斯可信区间分别为

[αl,α(l+N(1-γ))],[λl,λ(l+N(1-γ))],

③ 参数α,λ和βj,j=1,2,…,k的可信水平100(1-γ)%的最大后验密度可信区间近似为

[αl*,α(l*+N(1-γ))],[λ(p*),λ(p*+N(1-γ))],

l*,p*和q*满足如下条件

j=1,2，…k。

4 实验及分析

4.1 数据选择

选取咸阳纺织集团一分厂的同机型、同品种的50台细纱机，采集细纱机运行状态参数(如锭长、管纱长度、罗拉直径、前罗拉转速、自络纱疵、钳口隔距、锭速等)等数据，见表1，并分析细纱机的停机故障原因。

以30台细纱机的数据作为筛选和量化评估的样本库，用20台细纱机进行测试(现以代表性的JC7.29tex品种为对象，选择如锭子速度、前罗拉转速、中罗拉转速等性能参数)，见表1，并验证综合指标建立的有效性。

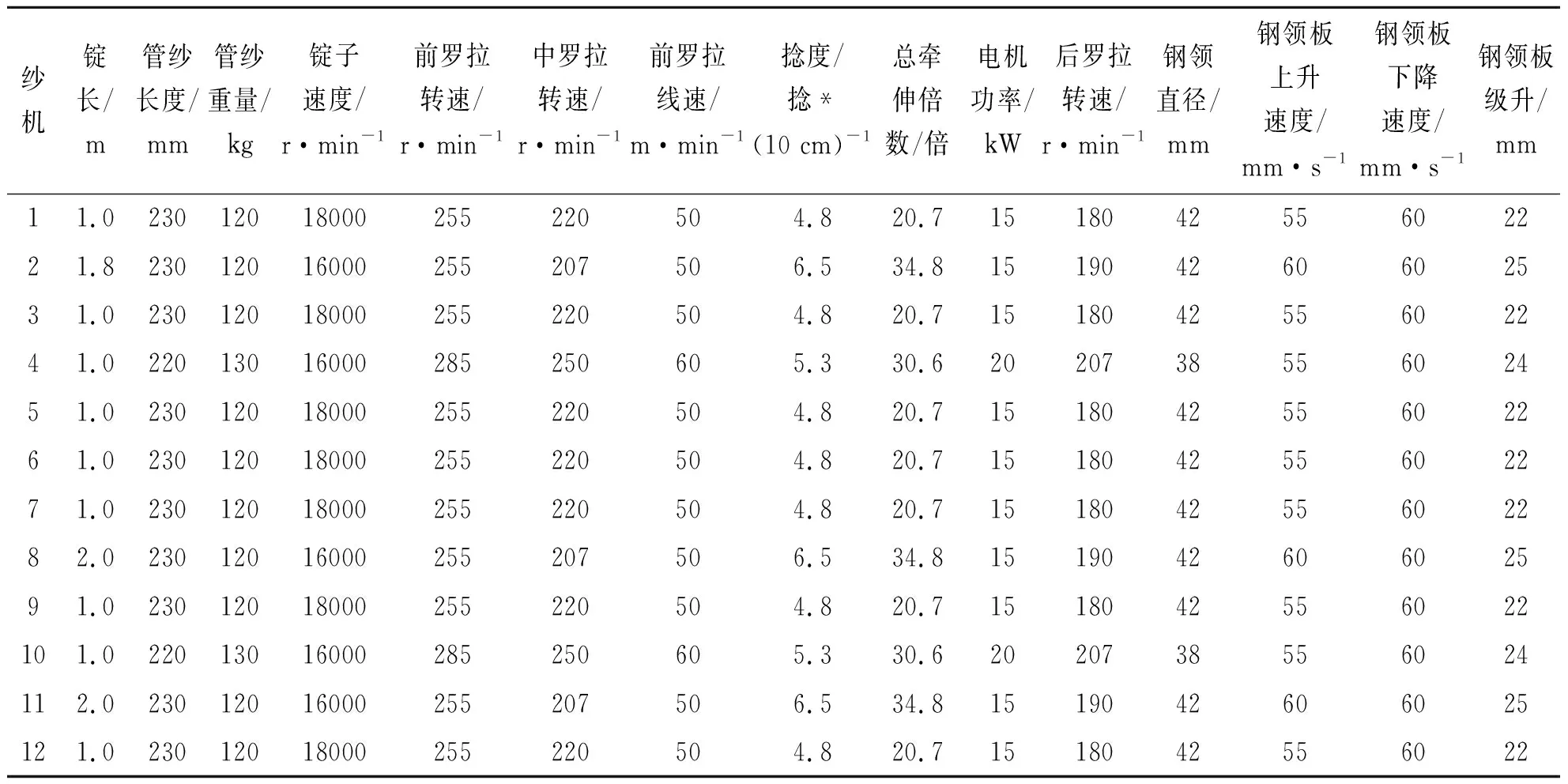
表1 整理后的20台细纱机的性能数据

续表1

4.2 综合指标建立

根据敏感度、相关度和重要度三个标准，对细纱机性能退化参数进行筛选和量化评估，得到的三个标准和综合标准权重变化如图1所示。由图1可知，在敏感度标准中，第4个参数(锭子速度)的计算结果最为显著，依次为第5个参数(前罗拉转速)、第7个参数(前罗拉线速度)、第9个参数(牵伸倍数)、第10个参数(电机功率)和第13个参数(钢领板上升速度)，就敏感度标准而言，上述六个参数基本符合要求。在相关度标准中，除了第6个参数(中罗拉转速)外，其他参数之间均存在强相关性，而且锭子速度、前罗拉线速、捻度、牵伸倍数之间关系最为显著。在重要度标准中，锭子速度的计算结果最为显著，依次为前罗拉转速、前罗拉线速、牵伸倍数、电机功率和钢领板上升速度，如图2所示，说明计算结果基本符合重要度标准。

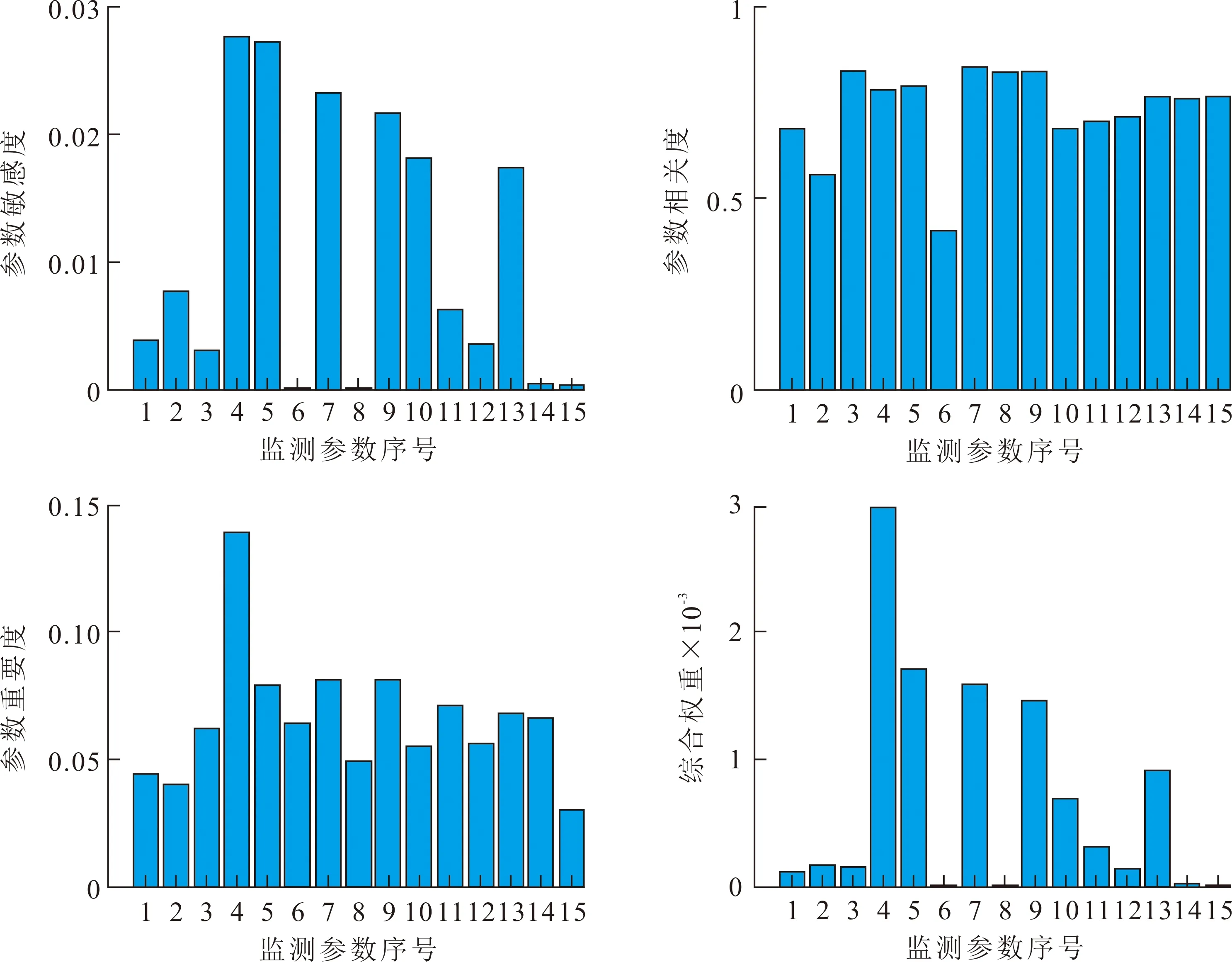
图1 细纱机性能参数筛选Fig1 Selection of performance parameters

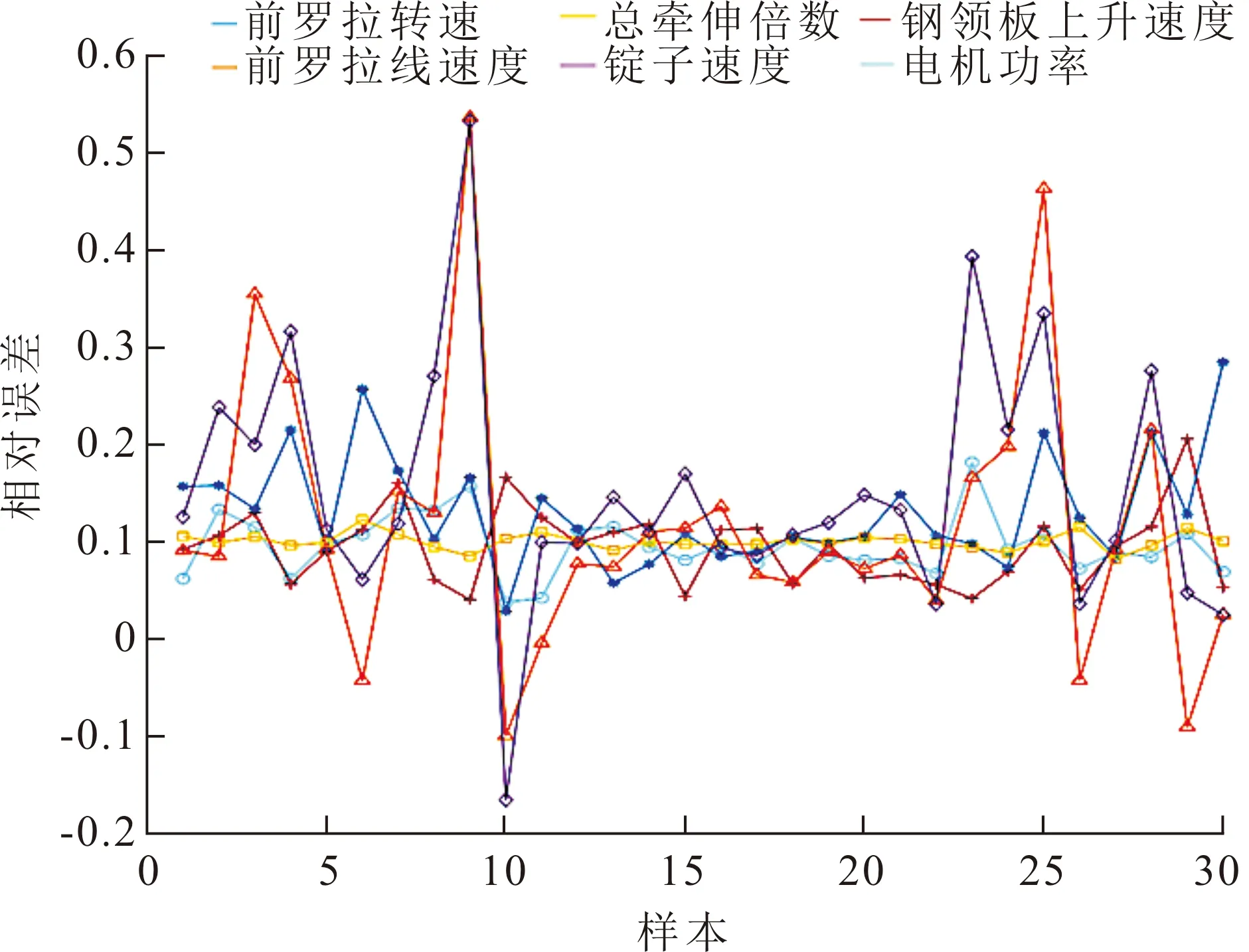
图2 细纱机性能退化参数之间关系

由此，在表1的基础上，根据式(6)、式(7)计算得到参数权重见表2，并将其作为综合指标融合的权重。

表2 参数权重

4.3 模型验证

在表3的基础上，利用退化数据进行拟合优度检验，具体的拟合优度检验系数计算公式为

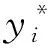
根据图3，仿真得到的拟合优度系数=0.945 7，结果说明建立的细纱机性能退化模型对退化指标的拟合程度较好。

图3 退化数据与预测数据的拟合优度仿真结果

为实现细纱机性能退化模型的拟合，对四种不同形式的 Copula 函数(Gumbel Copula、 Frank Copula、Clayton Copula 和 Gaussian Copula)分别进行建模以及参数估计，对细纱机外部环境变化进行分析，并对细纱机性能突发失效的影响进行检验，结果见表3。

表3 Copula函数AIC值

在表3中，根据AIC准则，选择AIC的最小值以及最小值对应的Gumbel Copula函数进行竞争失效模型验证，具体过程如下。

通过这些参数初始值可知，基于Copula函数的细纱机相依竞争失效模型比较符合实际生产。在此基础上，利用细纱机退化数据和失效阈值，实验验证得到的细纱机竞争失效可靠度曲线如图4所示。

图4 可靠性曲线对比

由图4可知，相依条件下的竞争失效可靠度R1与实际的竞争失效可靠度R2曲线之间呈正相关关系。这一结果说明，构建的细纱机竞争相依失效模型符合实际生产，而且具有较高的准确性。

4.4 性能指标退化前后的对比分析

在表2的基础上，利用式(20)至式(27)对构建的性能退化模型进行参数估计，得到性能退化的锭子速度、前罗拉转速、前罗拉线速度、总牵伸倍数、电机功率、钢领板上升速度等参数值详见表4。

由表4可知，性能退化后的锭子速度、前罗拉转速、前罗拉线速度、总牵伸倍数、电机功率、钢领板上升速度等参数值与表2中的参数值相比，从不同程度提高了3%～5%，尤其是钢领板上升速度、钢领板下降速度表现得更为显著，充分说明构建的相依竞争失效模型能够较好地描述细纱机的退化轨迹，而且有利于细纱机性能的可靠性评估。

表4 退化后的20台细纱机性能数据

在此基础上，将细纱机性能相依竞争失效模型应用于细纱机工序当中，对比分析应用模型前后成纱质量指标(细度不匀率、细节、粗节、断裂强度、断裂伸长率等)的变化情况，同时按纺纱厂的三班四运转模式，取一个班8 h的成纱数据进行测试，其结果见表5。

表5 纱线质量指标数据对比

由表5可知，经细纱机性能退化模型应用后，细度不匀率、细节、粗节、断裂强度、断裂伸长率等成纱指标均在数值上得到了提升。

同时，为验证细纱机性能退化模型的有效性，借助Matlab 2016a系统软件以及表5中的性能参数(如锭子速度、前罗拉转速、前罗拉线速度等)，将其文献[3]提出的基于正则化深度神经网络的预测维护方法、文献[5]构建的基于蒙特卡罗的细纱机系统故障仿真模型，以及文献[10]提出的一种面向细纱机的罗拉故障特征信息提取方法进行对比，其中四种方法预测性能参数的结果如图5所示。

图5 四种方法预测性能参数的结果

由图5可知，构建的性能退化模型对锭子速度、前罗拉转速、前罗拉线速度、总牵伸倍数、电机功率、钢领板上升速度等参数预测结果的相对误差较小。这说明该模型的性能优于文献[3]、文献[5]和文献[10]，而且该模型预测得到的性能参数值与实际值更接近，有利于细纱机性能的可靠性评估。

5 结 论

针对细纱机性能退化的问题，研究了性能退化的机理，引入敏感度、相关度、重要度三个标准，对细纱机性能退化参数进行了筛选和量化评估，构建了一种面向细纱机的性能退化模型。在此基础上，利用Weibull分布对细纱机的性能突发失效过程进行了预测，并利用Copula函数构建了一种面向细纱机性能退化的相依竞争失效模型，同时利用Gibbs算法对该模型进行了参数估计。

研究结果表明，构建的退化模型对综合退化指标的拟合程度达到了94.57%，有利于细纱机性能的可靠性评估，而且在相依条件下的竞争失效可靠度与实际的竞争失效可靠度曲线之间呈正相关关系，说明构建的细纱机竞争相依失效模型符合实际生产。同时，性能退化后的锭子速度、前罗拉转速、前罗拉线速度、总牵伸倍数、电机功率、钢领板上升速度等参数值与原参数值相比，从不同程度提高了3%～5%，尤其是钢领板上升速度、钢领板下降速度表现得更为显著，进一步充分说明构建的相依竞争失效模型能够较好地描述细纱机的退化轨迹，而且有利于细纱机性能的可靠性评估。