人字齿轮对称度偏差对系统振动特性的影响分析*

贾婧瑜，沈云波，曹建锋

(1.西安工业大学 机电工程学院，西安710021；2.中国航发湖南动力机械研究所，株洲 412000)

齿轮传动作为常见的机械传动方式之一，随着科学技术的快速发展，正朝着高速、重载、高精度的方向发展，这对其动态性能也提出了更高的要求。人字齿轮不仅具有传动稳定以及斜齿轮本身承载能力高的优点，而且克服了斜齿轮轴向力对支承轴承的磨损，使其成为航空发动机、船舶动力等高速、重载、大功率传动的重要传动形式。然而人字齿轮两侧轮齿存在不可避免的非完全对称，是引起人字齿轮产生偏载、轴向振动、噪声的主要根源，严重影响齿轮系统的寿命、可靠性等使用性能[1]。

由于引起齿轮振动的因素很多，分析各因素对各种齿轮传动系统的影响，对了解系统振动的来源具有重要意义。文献[2-3]建立了简化的集中质量模型，分别研究了直齿轮传动过程中动态传动误差、传动误差的高次谐波成分、齿轮传动中时变啮合阻尼对齿轮系统动态特性和动态稳定性的影响。然而该集中质量模型仅局限于直齿圆柱齿轮系统的动态行为和振动特性的分析。文献[4]研究了由多个部件组成的齿轮系统振动情况，并通过模态分析得到了齿轮系统的振动特性和齿轮的动载荷系数。但该研究主要解决是的直齿圆柱齿轮系统的振动分析，且没有涉及轴向振动的问题。文献[5]研究了人字齿轮轮齿两侧载荷变化情况，通过求解啮合线上的柔度来获得人字齿轮副的啮合刚度。但该研究主要针对轮齿对称情况下的人字齿轮，没有考虑对称度偏差对啮合刚度的影响。文献[6]建立了可用于变速动态分析过程的人字形行星齿轮动态模型，得到了人字齿轮在忽略齿廓误差情况下加速过程的动态响应分析。但该研究尚未考虑人字齿轮两侧轮齿对称度偏差对系统轴向振动的影响。文献[7]在理论和实验方面研究了在不同转速和扭矩下人字齿轮系统的动态特性。不过在理论和实验中未考虑对称度偏差对轴向振动的影响因素。文献[8-10]分别采用ANSYS有限元软件的接触分析模块，和螺旋锥齿轮的载荷接触分析模型，对齿轮传动进行静态接触分析，从而得到完整啮合周期内的时变啮合刚度，为本文具有对称度偏差的人字齿轮传动啮合刚度的计算提供了方法。在人字齿轮动力学研究方面，文献[11-12]利用TCA和LTCA技术计算了人字齿轮的内部激励，建立了人字齿轮系统动力学模型，在时域和频域内分析了系统沿不同方向的振动情况。文献[13-14]构建了人字齿轮系统动力学模型，考虑了时变啮合刚度、综合啮合误差等重要因素，对在使用过程中齿距累积误差对系统的动态特性产生的影响进行了研究。但文献并没有考虑人字齿轮对称度偏差对啮合刚度和轴向振动情况的影响。文献[15]进行了人字齿轮传动小轮轴向固定和轴向窜动对齿面载荷分布的影响的研究，采用齿面承载接触分析的方法，根据齿面偏载情况，提出了通过人字齿轮复合修形设计获得左右齿面载荷均匀分布方法，并确定了最佳修形量。然而该文献中人字齿轮对称度偏差与偏载量的关系，缺乏系统的描述。文献[16]研究了人字齿轮减速器传动系统动力学模型的建立，分析计算了时变啮合刚度和传递误差的变化情况，得到了时域和频域内系统的振动响应，但该研究没有考虑对称度偏差对人字齿轮时变啮合刚度的影响。文献[17]研究了高转速下人字齿轮传动系统沿轴向的振动特性，分析了螺旋角误差、时变啮合刚度和综合齿形误差激励下系统的轴向振动情况。但文献仍未考虑对称度偏差对人字齿轮传动系统振动的影响情况。

文中旨在提出并建立考虑对称度偏差的人字齿轮系统多自由度动力学分析模型，研究对称度偏差对人字齿轮传动系统轴向振动的影响，并验证了理论分析结果与实验结果变化规律的一致性。

1 人字齿轮对称度偏差

人字齿轮是由两个螺旋角相等、方向相反的斜齿轮构成。如果要求两侧轮齿的同侧齿面围绕中心平面对称，那么齿轮左右的同一位置的轮齿上的螺旋特征也围绕中心平面对称。

图1给出了人字齿轮沿齿轮分度圆柱面展开时对称度偏差的定义。即人字齿轮左右两侧斜齿轮同一侧齿面上的理论螺旋线的交点O应位于中心平面上。但由于齿轮加工和制造误差，实际两侧齿面的螺旋线在分度圆柱展开平面上的交点偏离到中心平面的H点，那么实际交点H与中心平面之间的距离就定义为人字齿轮的对称度偏差fA。

图1 对称度偏差的定义Fig.1 Definition of symmetry deviation

根据对称度偏差的定义，并考虑齿轮齿距测量的方法，构建了螺旋线法[18]人字齿轮两侧轮齿对称度偏差测量模型，建立的对称度偏差测量坐标系如图2所示。

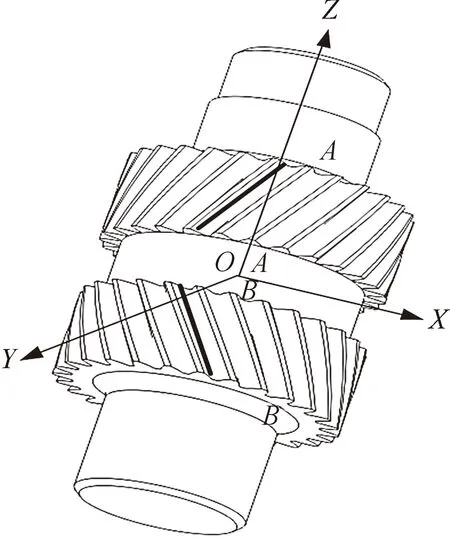
图2 齿轮测量坐标系

在图3所示的数控CNC齿轮测量中心对人字齿轮的对称度偏差进行了测量，所测量的齿轮参数见表1。

表1 试验所用人字齿对的基本参数

图3 人字齿轮对称度偏差测量Fig.3 Measurement of symmetry deviation of herringbone gears

小轮的对称度偏差测量结果如图4所示，其中横坐标为齿的序号，纵坐标为相邻齿的对称度偏差。可以看出，15号齿和16号齿间的对称度偏差较为明显。

图4 小齿轮相邻齿对称度偏差的测量结果Fig.4 Measurement results of full tooth helix of pinion

对采样数据进行处理，采用统计分析的方法获得了小轮的对称度偏差为fa1=0.025 mm。利用同样的测量原理和方法，测量出大轮的对称度偏差为fa2=0.048 mm。

2 人字齿轮系统动力学模型

2.1 十二自由度动力学分析模型

人字齿轮中两对斜齿轮的结构和材料属性是相同的，但由于对称度偏差对齿轮啮合的影响，左右两组斜齿轮副的啮合刚度有所不同。将齿轮轮毂和轴视为一个整体，忽略轮毂和轴的连接形式，将人字齿轮退刀槽部分看作刚体，左右两侧斜齿轮视为刚性连接，对称度偏差造成的啮合刚度变化会使得原本人字齿轮两侧对称分布的轴向力发生变化，从而引发轴向窜动。建立考虑对称度偏差的人字齿轮传动系统动力学分析模型，如图5所示。

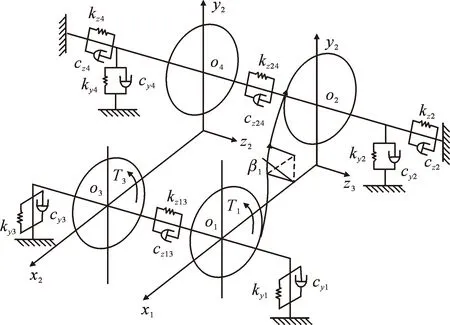
图5 弯-扭-轴耦合人字齿轮振动模型

根据牛顿第二力学定律，系统的动力学方程可以由图5中得到：

(1)

(2)

(3)

(4)

式中：yi,zi,θi(i=1，2，3，4)分别为主动轮和从动轮中心点O1,O2,O3和O4在z方向和y方向的平移量和角位移量；m1,m2,m3,m4,I1,I2,I3,I4分别为人字齿轮左侧和右侧斜齿轮的质量及转动惯量；β1为人字齿轮的螺旋角；Fy1,Fy2为人字齿轮左右两侧斜齿轮副的切向啮合力；Fz1,Fz2为人字齿轮左右两侧斜齿轮副的轴向啮合力；Rb1,Rb2分别为主动轮和从动轮的基圆半径；cy1,cy2,cy3,cy4,ky1,ky2,ky3,ky4为每个滚动轴承在径向的支撑阻尼和支撑刚度；cz2,cz4,kz2,kz4为从动轮在轴向的支撑阻尼和支撑刚度；cz13,cz24,kz13,kz24为左侧和右侧斜齿轮中间退刀槽部分在轴向的拉、压阻尼和刚度；Fs1(t),Fs2(t)为人字齿轮左侧和右侧斜齿轮副的啮入冲击激励；T1和T3分别为小齿轮两侧主动轮的输入扭矩。

其中，由于啮入冲击时间很短，因此通常将啮合冲击力曲线简化成锯齿波函数来处理。从图6所示的啮入冲击力曲线可以看出对称度偏差对人字齿轮轮齿两侧的啮合冲击影响较小。

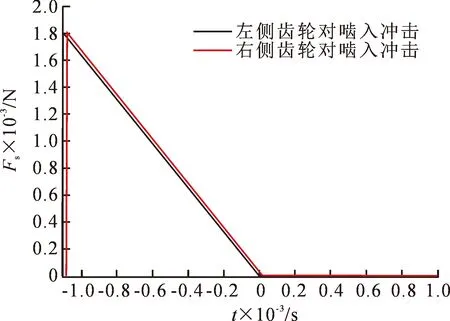
图6 啮入冲击力曲线图

通过龙格-库塔法求解可得到人字齿轮主从动轮在轴向和径向的振动位移和振动速度，以及扭转变形量和齿轮在轴承处的支承力变化情况。

2.2 有限元法求解齿轮啮合刚度

使用Abaqus对人字齿轮啮合刚度进行仿真时，由于考虑到轮毂和轴等支承结构增加模型的计算量影响计算精度，为了获得准确的啮合刚度，需要简化人字齿轮系统模型。对人字齿轮三维简化模型进行相关的网格划分，因齿轮轮齿和轮毂的网格密度不同，剖分后分别划分网格。齿轮轮齿先剖分出一个齿，生成端面的面网格，同时采用软件的实体映射划分功能对单个斜齿的体网格进行生成(如图7所示)，进而得到整个斜齿轮的体网格。因所研究人字齿轮考虑到对称度偏差的影响，在实际模型中可以看作两侧轮齿并非完全对称，而是一侧斜齿轮相对另一侧含有微小的圆心角偏移。则最后需要对斜齿轮网格进行复制和旋转命令，使其成为目标网格，即生成含有对称度偏差的人字齿轮体网格，如图8所示。

图7 单个斜齿的网格划分Fig.7 Meshing of a single helical tooth

仿真使用的齿轮模型参数与之前所测齿轮参数一致。仿真时约束了除两齿轮绕轴旋转的自由度外所有自由度，在小齿轮上施加一个较低的准静态速度，在大轮上施加一个额定的负载扭矩，进行齿轮啮合传动的准静态仿真。图9为齿轮啮合模拟中某时间的啮合状态。由Abaqus得到的啮合刚度曲线(图10)可以看出，由于对称度偏差存在，人字齿轮两侧斜齿轮副啮合刚度曲线存在偏差，右侧斜齿轮副的啮合刚度略小于左侧齿轮副的啮合刚度。

图9 齿轮啮合模拟中某时间的啮合状态Fig.9 Meshing state at one point in the simulation of gear mesh

图10 人字齿轮左右侧的啮合刚度Fig.10 Meshing stiffness of the left and right sides of the gear

2.3 人字齿轮系统轴向振动特性仿真

根据测得的对称度偏差，可得知人字齿轮传动系统中主动轮中左旋相对右旋偏差0.025 mm，从动轮中左旋相对右旋偏差0.048 mm。进一步求得主动轮两侧轮齿圆心角偏移量为54″，从动轮两侧轮齿圆心角偏移量为35″，人字齿轮传动动力学参数见表2。人字齿轮传动的振动情况可以根据给出的动力学模型计算，得到人字齿轮的轴向振动速度如图11所示。

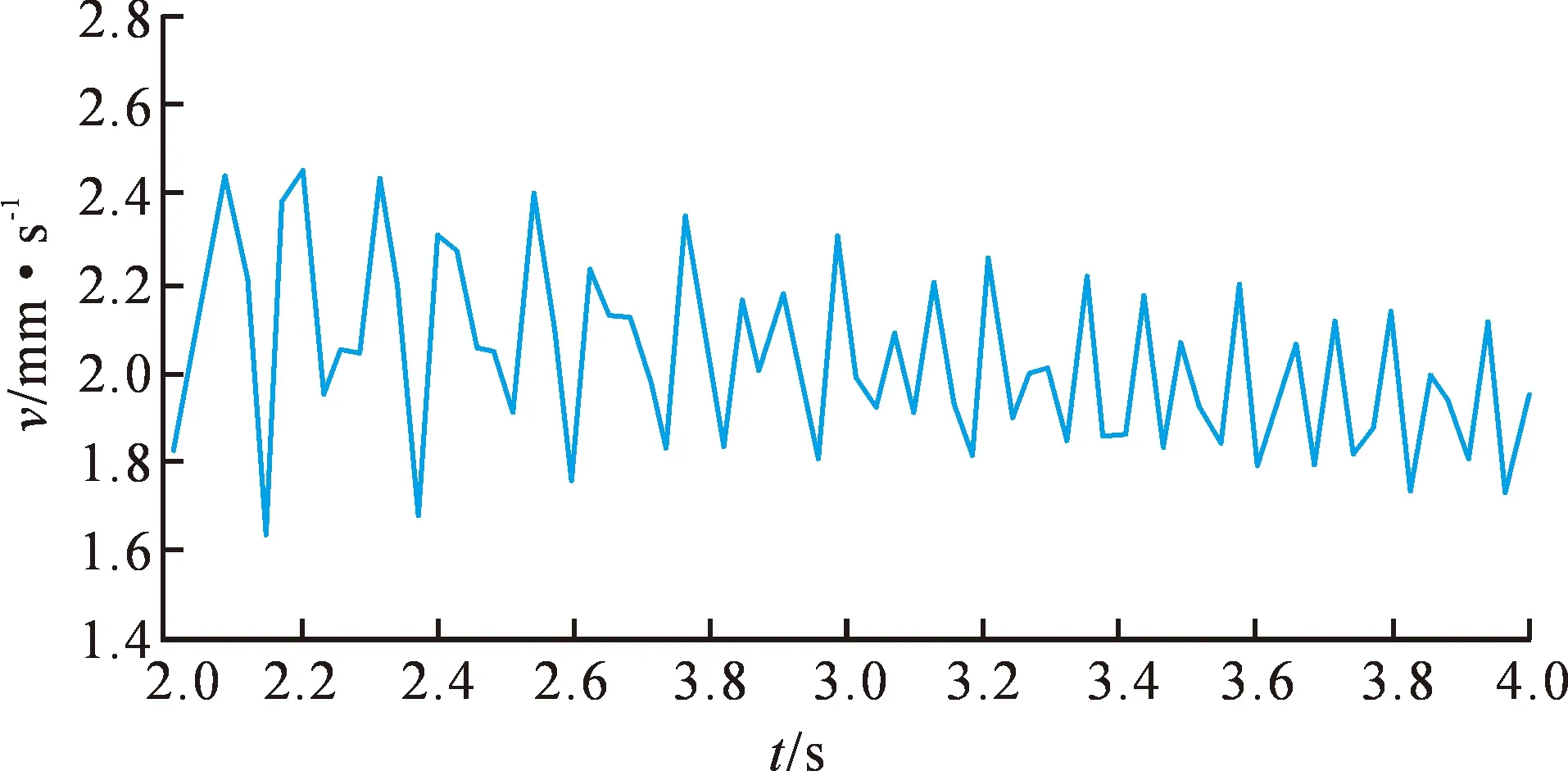
图11 对称度偏差为0.025 mm时的轴向振动速度

表2 人字齿轮传动动力学参数

3 实验验证和分析

3.1 封闭功率流人字齿轮试验台

与传统的开放功率流试验台相比，本次实验中使用的封闭式功率流试验台更加节能。封闭式功率流意味着能量传输的路线在整个测试台中形成一个闭环。变频逆变系统使加载设备消耗的部分能量转化为电能，然后再传输回驱动系统达到加载和节能的效果。振动速度传感器型号为CYT9200，测量范围0～50 mm·s-1，系统采样频率2 000 Hz。

试验台的布局如图12所示。在测试和测量过程中，传感器分别在输入轴的轴向90°，180°和270°三个测量点进行测试。

图12 人字齿轮试验台布局

3.2 测试结果的验证分析

人字齿轮在不同速度和扭矩下的振动速度是由试验台测量的。以时间为横坐标，以小齿轮右侧沿Z方向的振动速度为纵坐标，得到三个测量点的振动速度对比图。

图13所示为人字齿轮在转速为8 00 r·min-1、1 200 r·min-1，1 500 r·min-1时分别沿轴向的振动速度。可以看出，当测量点和扭矩保持不变的条件下，转速的增加导致了振动速度的增加；同样在1 500 r·min-1时，明显看出相对比其他两种情况下齿轮的轴向振动速度波动更大。

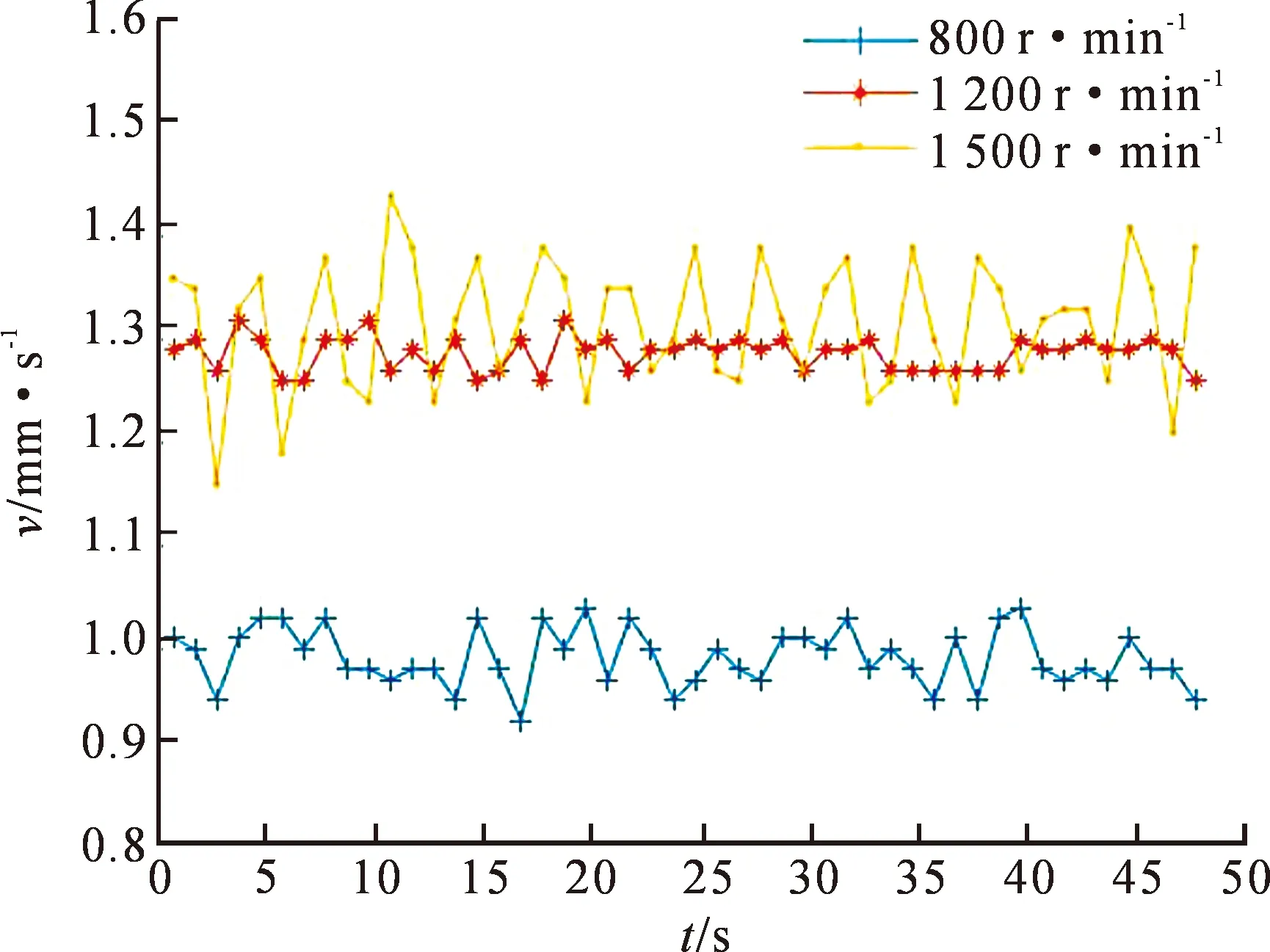
图13 恒定扭矩下不同转速下的振动速度比较Fig.13 Comparison of the vibration speeds at different revolutions per minute with constant torque

图14所示为转速为1 000 r·min-1时不同扭矩情况下齿轮沿轴向的振动速度对比图。可以看出，在测量点和转速不变的条件下，扭矩的增加导致振动速度增加；同时当扭矩较大时，齿轮在轴向的振动速度波动较大。

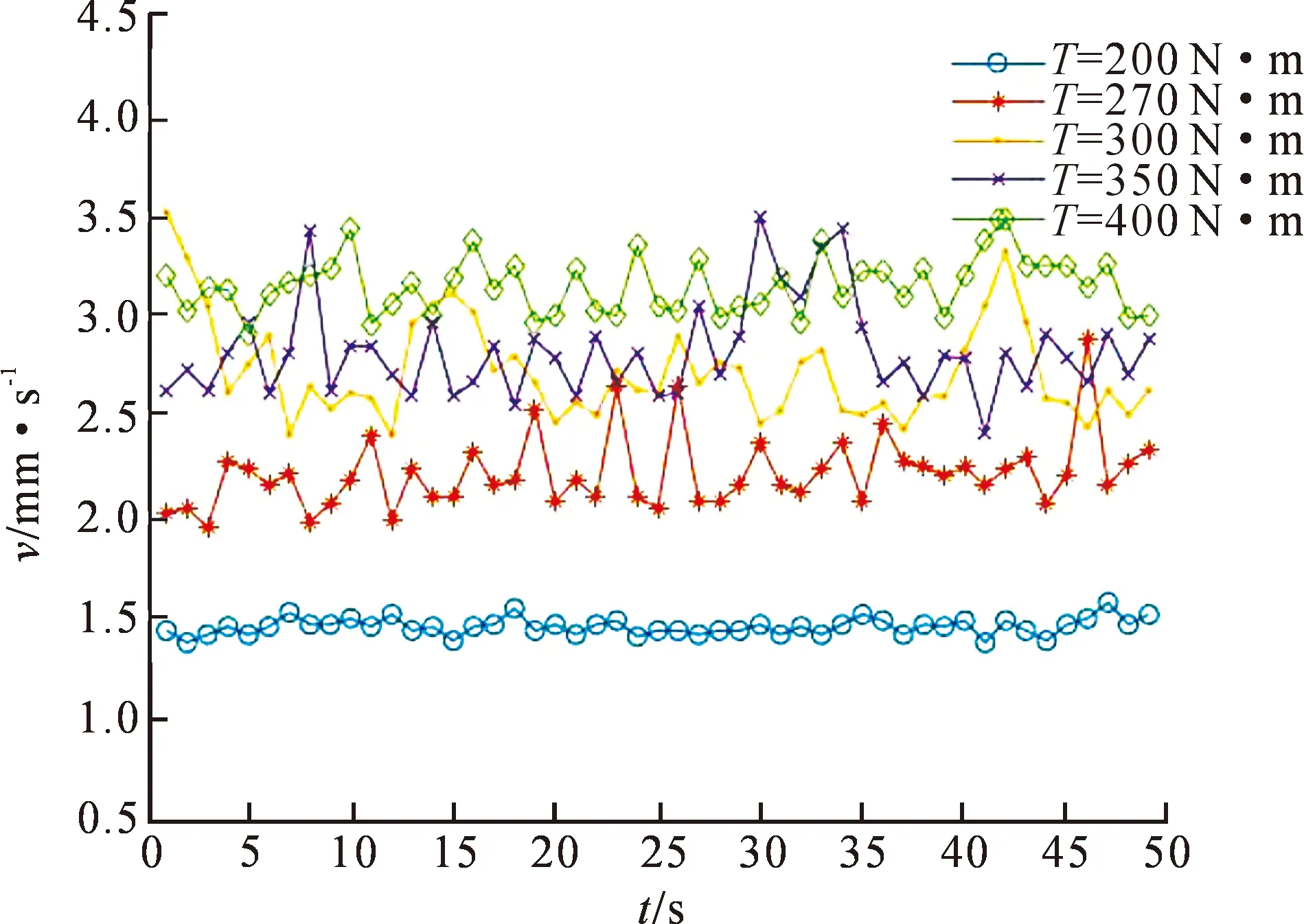
图14 恒定转速不同扭矩下的振动速度Fig.14 Comparison of vibration speed at 1 000 rpm with different torques

图15所示为齿轮在800 r·min-1，1 200 r·min-1，1 500 r·min-1时齿轮沿轴向的振动速度对比图。得到在转速和扭矩不变的条件下，测量点移动振动速度的变化规律。当转速为800 r·min-1和1 200 r·min-1时，三个测量点的振动速度变化幅度不大，但当转速达到1 500 r·min-1时，明显看到随着测量点位置的变化，振动速度逐渐变快，表现出对称度偏差对齿轮轴向振动的影响。

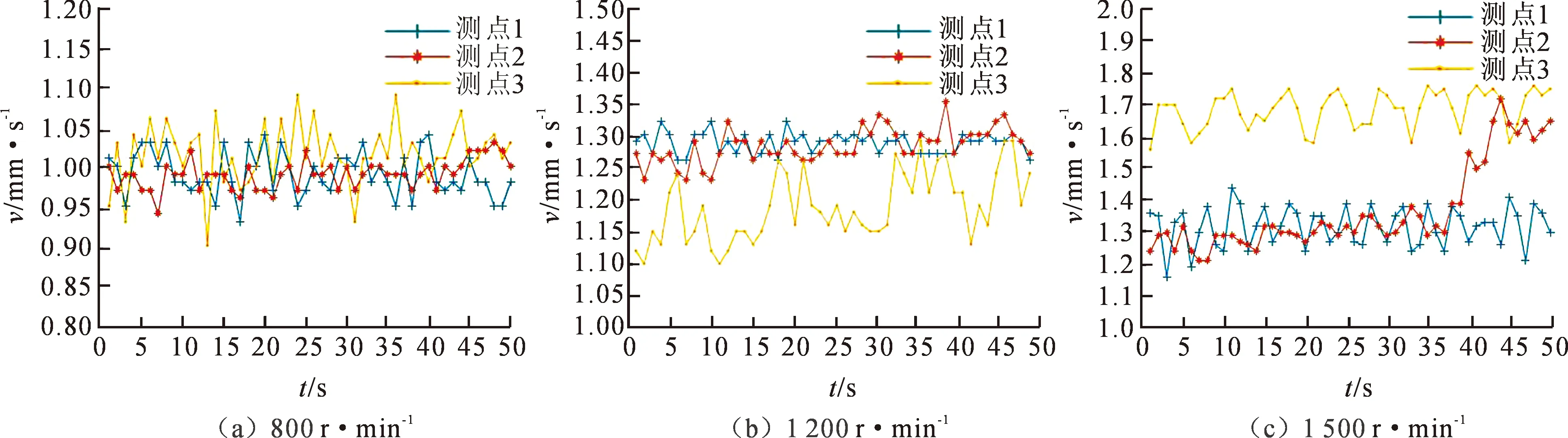
图15 不同扭矩下的振动速度比较

为了进一步评估模型的准确性，对人字齿轮在1 000 r·min-1时测量结果和理论结果进行直接比较。从图16中可以看出，响应曲线的整体形状都吻合得很好，尽管可以看到有小数量的误差，但模型和实验之间的合理一致性仍然相当明显。

图16 人字齿轮测量和理论仿真的响应曲线的比较

4 结 论

1) 建立了考虑人字齿轮两侧轮齿对称度偏差的传动系统12自由度弯-扭-轴动力学分析模型，并采用有限元法精确求解了考虑对称度偏差影响的两侧轮齿啮合的时变啮合刚度，结果表明了对称度偏差明显减少了齿轮副的综合啮合刚度。

2) 采用齿轮齿距测量法获得了小轮的对称度偏差为0.025 mm，大轮的对称度偏差为0.048 mm；运用龙格-库塔法求解了动力学方程，获得了不同工况下传动系统轴向振动速度；搭建了封闭功率流人字齿轮传动试验台，在实际扭矩和速度范围内对人字齿轮进行实验，测试结果表明扭矩和转速的增大会造成振动速度的增加；理论分析结果与实验结果直接比较表明小轮轴向振动速度变化趋势具有高度的一致性。

3) 文中获得的理论分析结果仅考虑了不同工况下的齿轮系统的动力学行为，因而与齿轮箱表面实验测试数据对比误差较大。考虑齿轮箱的动态特性，建立齿轮系统和箱体的耦合动力学分析模型并探究齿轮箱体耦合振动情况，是进一步研究的方向。