大跨度叠层连廊步行振动响应及减振控制研究*
薛 磊
(中铁第一勘察设计院集团有限公司,西安 710043)
随着城市经济的快速发展和建筑功能要求的不断提高,连体建筑越来越受到广大业主的欢迎。然而当人行步频与连廊结构竖向基频接近时,容易产生共振效应,使人产生心理恐慌,从而影响结构的使用功能[1]。因此,振动舒适度已成为连廊设计的一个重要指标。近20年来,学者对如何消除共振产生的不利影响做了大量研究工作。文献[2-3]等通过提高结构的抗力储备、隔离振动源来降低振动并防止潜在的结构损坏。结果表明,增加结构刚度、隔离振动源能有效减小结构的动力位移,提高居住者的舒适度,但未考虑耗能构件的设置,经济性不足。文献[4-5]等通过采用不同的被动调谐质量阻尼器(Tuned Mass Damper,TMD)系统设置方案来加大结构的阻尼,消减由于频率耦合造成的结构共振现象。结果表明,TMD的耗能能力较强,减振效果明显,但未研究被动调谐质量阻尼器(TMD)不同设置位置对结构动力特性的影响。文献[6]阐释了被动TMD和主动质量阻尼器(Active Mass Damper,AMD)的差异。结果表明,两种装置均可以有效缓解共振响应,但相比而言,AMD的振动控制效率较低。文献[7]提出了一种分析高层建筑TMD动力响应的新方法。结果表明,TMD分布不能显著控制结构在地震荷载作用下的振动。文中汲取文献[2-7]研究成果,基于西安站东配楼改造工程,通过对舒适度评价标准及振动响应因素的分析,获得了适用于大跨度叠层连廊结构的舒适度评价指标及采用被动调谐质量阻尼器(TMD)系统有效的、新型的减振控制措施。
1 工程概况
西安火车站(改扩建)东配楼项目总建筑高度35.5 m,地上6层,地下2层(局部1层),建筑面积约9.3万 m2。受场地条件及整体规划方案的制约,东配楼将被分割成三个平面极其不规则的建筑单体,各单体间采用大跨度连廊进行连接。大跨度连廊由单层桁架和叠层桁架组成示意如图1所示。
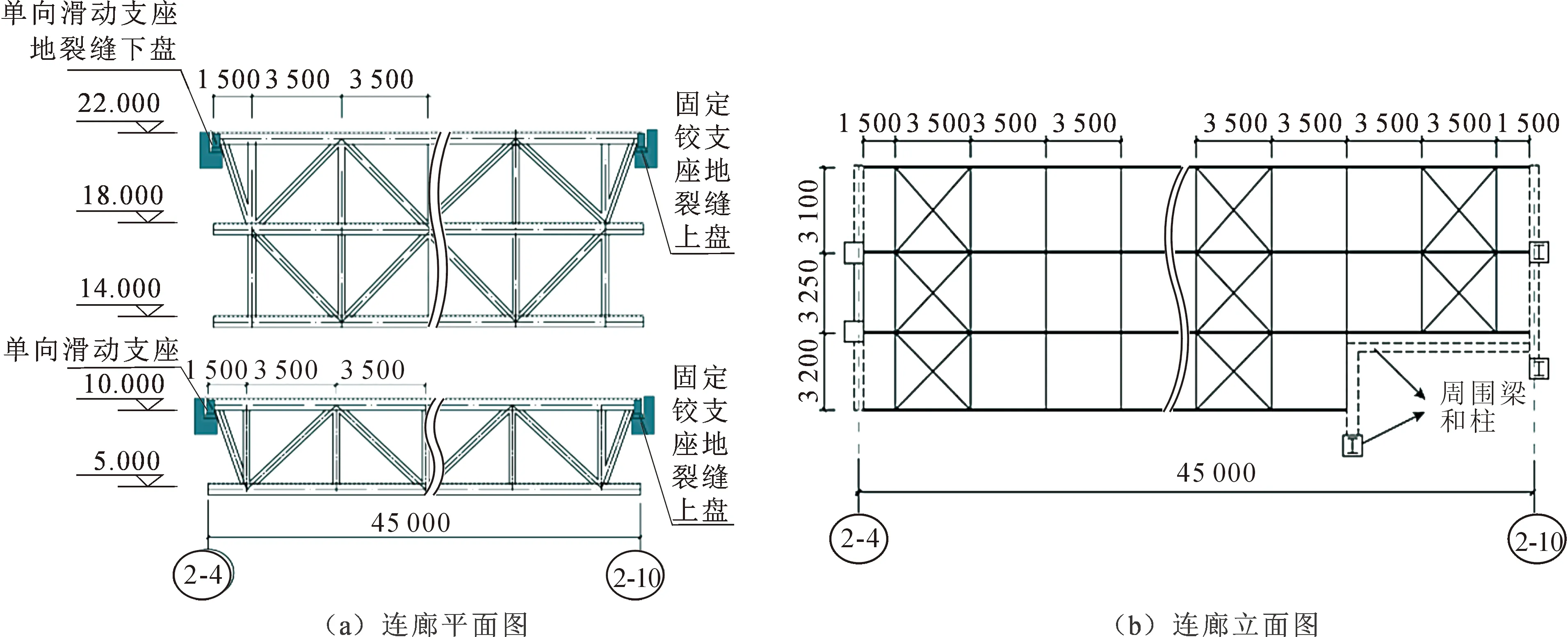
图1 大跨连廊示意图
连廊区域和桁架区域分别采用上铰接下滑动和左铰接右滑动的弱连接支座形式。整个桁架采用上弦支承,由4榀跨度为52 m、节间宽为4.8 m的平面桁架组成。每榀桁架通过钢梁连接,每隔1.4 m设置水平支撑以确保平面稳定性。
2 荷载工况及舒适度评价标准
2.1 荷载工况
人致激励荷载可分为单次激励和连续激励两大类。单次激励指单人行走时对楼板某一节点位置的一次响应;连续激励指人群行走时对某一点的多次响应。根据相关研究表明[8],由于激励方式的不同,单次激励引起的楼板响应不一定比连续激励时的小,因此需对人的步行荷载特性进行研究。
典型的单足落步竖向作用曲线选自文献[9]早期对单人行走荷载进行了试验研究,如图2(a)所示。图中(0,0)点表示足跟开始与地面接触,然后随着人体重心的转移曲线逐渐升高,当为1.2 G~1.5 G时,达到第一个峰值点,该峰值点包括人体自重和惯性作用力的总和。随着腿的摆动和重心的前移,曲线逐步下降,接着人脚掌蹬地,使得曲线再次升高,后峰值点作用力较前点略低,约为1.1倍左右,之后曲线迅速下降。
人群荷载选取文献[10]中的人行荷载曲线,如图2(b)所示。该荷载基于文献[11]对人连续行走的研究成果,认为行走时产生的激励力可以用傅里叶级数表示,阶数较大的简谐分量随着频率的增加在总激励中所占的比重逐渐减小。
人跑动时对连廊的冲击力曲线参考文献[12]提出的不连续半波时程函数进行取值。一个跑动周期内人脚与地面接触时的荷载为一个峰值较大的半波曲线,同时,忽略离地后时间段内对连廊产生的作用力,荷载曲线如图2(c)所示。

图2 荷载工况曲线
文献[13]对户田公园人行桥的研究表明,当连廊上有一群人在行走时,人群密度会对行人步长和步速产生较大的影响,人群密度越大则步频越低。根据我国建筑楼盖振动舒适度技术标准:JGJ/T441—2019规定,将人群密度将行走特点分为5个等级,见表1。
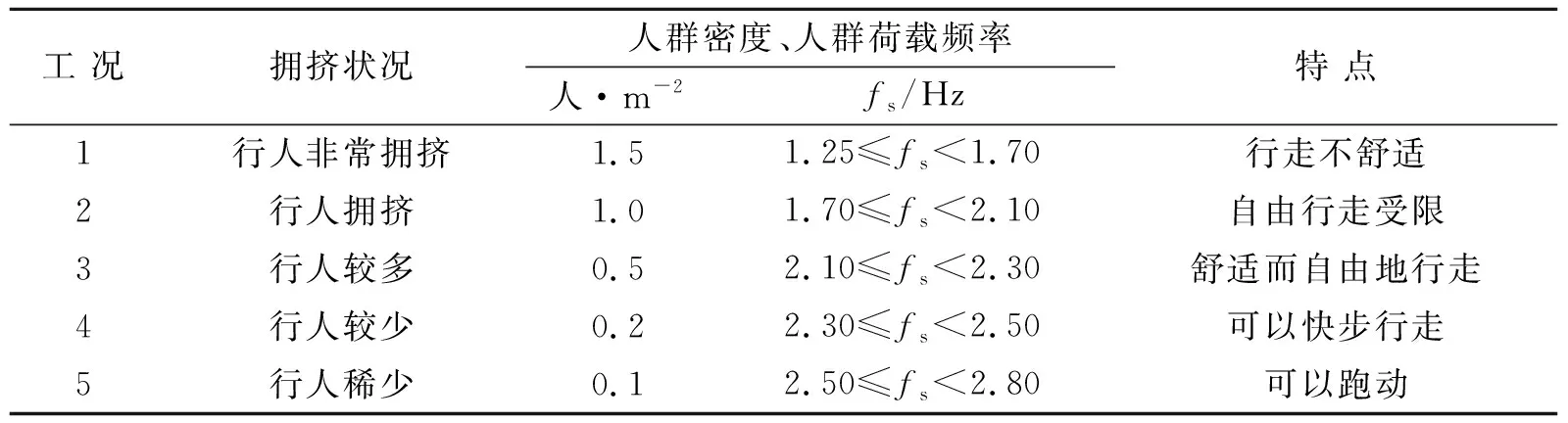
表1 人群密度与人群荷载频率关系
2.2 舒适度评价标准
人体对振动响应非常敏感,过大的振动会引起行人的不适感。美国规范与我国《城市人行天桥与人行地道技术规范》(JJ 69—95)的控制方法都是对人行桥的一阶自振频率进行限制。另一种舒适度评价方法,就是控制加速度响应的办法来反映结构的舒适度。对于5Hz以下的情况,不同国家和地区竖向加速度限值要求不同,见表2。

表2 加速度峰值评价标准
考虑到文中所分析大跨度叠层连廊的结构类型和使用环境,文中选用美国AISC-11标准中的加速度限值(0.15 m·s-2)作为控制指标。
3 仿真结果及分析
3.1 动力特性分析
采用SAP2000 有限元分析软件建立叠层桁架的空间有限元模型,桁架中杆件采用框架单元,楼板采用轻质楼面板,忽略楼板提供的刚度,采用无属性仅起荷载传递作用的虚面单元来模拟。荷载取值为:恒荷载1.5 kN·m-2,包括轻质楼板自重及面层自重,活荷载为3.5 kN·m-2;屋面为轻钢不上人屋面,恒载取为1.0 kN·m-2,活载为0.5 kN·m-2。动力分析时的荷载组合取1.0恒载+0.5活载,各杆件截面尺寸见表3。

表3 杆件截面尺寸
采用Ritz向量法进行分析,选取前50阶振型进行计算,保证结构的竖向振型质量参与系数不小于90%,前6阶振型模态如图3所示。

图3 大跨连廊前6 阶振型模态
模态分析结果表明,结构的第1阶振型以横向振动为主,频率为1.64 Hz。第2阶和3阶振型分别以扭转振动和横向振动为主。第1阶以竖向振动为主的振型为结构的第4阶模态,频率为4.29 Hz。虽然该频率离人正常活动的步频较远,但有可能与步频的2阶频率分量发生共振效应,因此,需要对该大跨度叠层连廊进行人致竖向振动响应分析。
3.2 连廊加速度响应分析
进行动力时程分析时,采用模态法进行分析,模态阻尼比取0.02。同时,人群荷载采用人群荷载密度进行模拟,并计算所有工况下步频对应的加速度响应,取最不利情况。计算结果显示,叠层连廊在各工况下,加速度响应最大位置位于外侧跨中节点处。
最不利加速度响应出现在连廊外侧跨中节点处,最不利工况下的结构自振加速度时程曲线如图4所示。
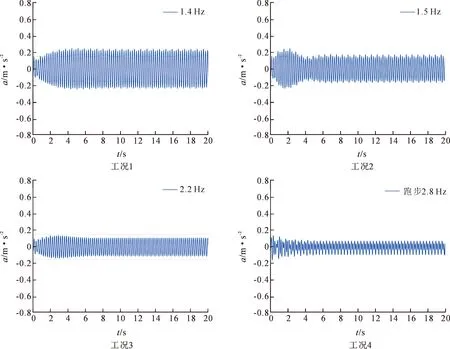
图4 最不利工况的结构自振加速度时程曲线
从最不利工况下加速度响应时程曲线可以看出,叠层连廊在受到1.4 Hz和1.5 Hz步频外荷载时的响应呈共振状态,最大位移节点的加速度最大达到0.242 m·s-2,超过了舒适度限值0.15 m·s-2。叠层连廊频谱响应曲线如图5所示。
从图5可以看出,当行人以1.4 Hz行走时,与其3阶频率分量4.2 Hz引发共振;当以2.1 Hz行走时,也与4.2 Hz引发共振,但造成的共振响应比步频1.4 Hz的3阶分量小。其原因是因为虽然2.1 Hz相比于1.4 Hz的人行荷载频率分量大且作用力大,但人群密度和等效响应系数却有所不同。这也说明了结构的加速度响应不仅仅取决于步行频率,还与步行力大小和人群密度以及人群的等效响应系数有关。
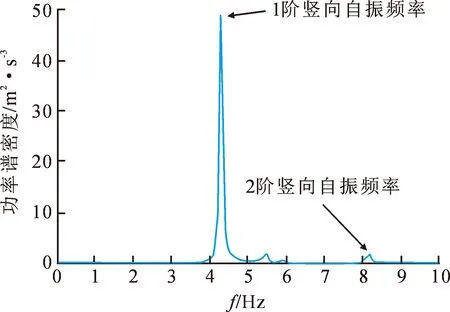
图5 跨中节点频谱曲线
3.3 考虑随机性人行荷载下的振动响应分析
为分析行人分布的随机性,将连廊以板块为单位进行分区(共78个分区),每个分区上的人群密度随机服从0.1人·m-2到1.5人·m-2的均匀分布。同时,每个分区上的行人个数采用相同的随机人行荷载曲线,并将曲线以面荷载的形式施加于楼板上。计算500次,并将计算结果进行统计分析,得到叠层连廊的加速度响应概率密度分布,如图6所示。
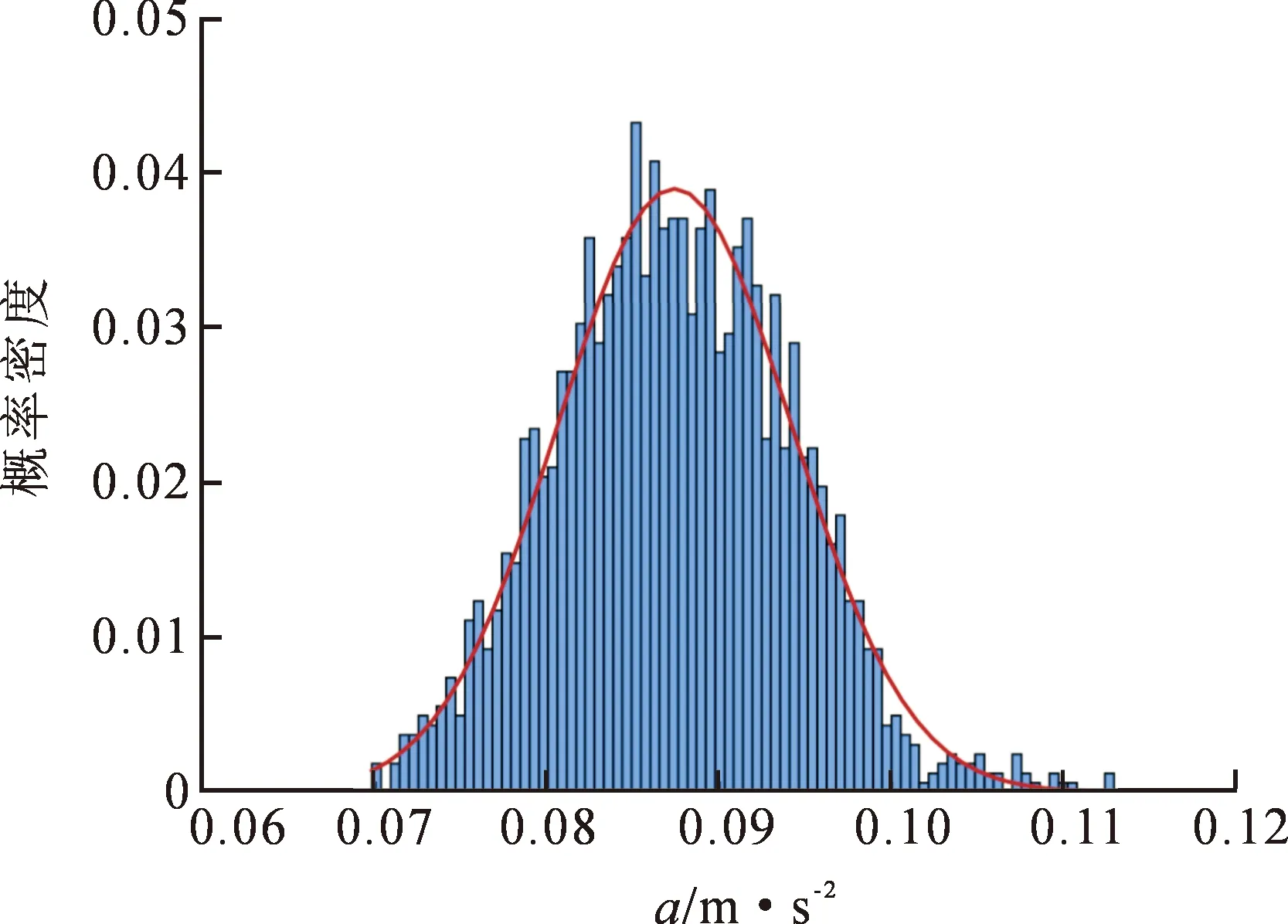
图6 加速度响应概率密度分布图
结果表明,整个时间段内的加速度分布形式类似于正态分布。将数据进行正态分布拟合,得到的加速度均值和标准差。由数据分析可知,在叠层连廊500次计算的随机工况样本中,加速度均值为0.087 m·s-2,置信区间为[0.074,0.101],意味着一个加速度时程内绝大部分时间的加速度会落入0.136~0.198 m·s-2的区间内,只有5%的时间超过了0.15 m·s-2的舒适度限值要求。从概率的角度来说发生舒适性问题的概率较低,因此,用等效响应系数的方法来分析振动响应是合理的。
3.4 连廊振动响应的影响因素分析
3.4.1 楼板厚度
连廊的自振特性由质量和刚度决定,其一部分来源于楼板,所以楼板的刚度直接影响到结构对于外荷载的响应大小。本节通过对不同楼板厚度的分析,研究楼板对于结构响应的影响规律。为方便计算,采用单层连廊模型。楼板选择混凝土材料,厚度从80~180 mm。人行荷载采用连续人群荷载曲线,频率采用不同板厚下对应的1/2倍竖向基频。图7为模型的竖向基频和跨中节点加速度峰值。
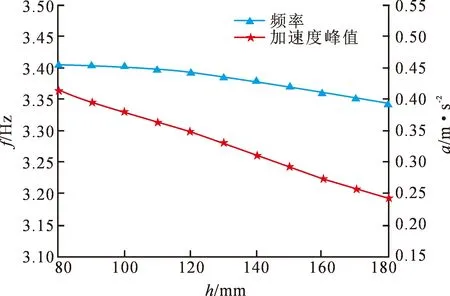
图7 结构自振频率及跨中加速度峰值与板厚的关系曲线
由图7可知,连廊板厚由80 mm逐渐增大到180 mm的过程中,结构一阶竖向自振频率由3.405 Hz降到了3.343 Hz,下降率仅为1.8%。但峰值加速下降了36.9%。由此说明,对板而言,桁架提供的刚度要远大于板提供的刚度,因此,板厚对结构频率的影响要比加速度的影响小。
3.4.2 人与结构的相互作用
为了解人与结构的相互作用对结构振动产生的影响,通过建立了人-结构耦合简化模型,进行阻尼比的计算,分析了人体阻尼与结构响应之间的关系。阻尼比采用动力学中的共振放大法为
(1)
式中:Rd为动力放大系数;μ0为共振时的最大位移;ωn为频率;μst为静力作用下的位移。
为验证人体阻尼对结构振动的影响,建立一简支梁模型。简支梁跨度为24 m,截面尺寸600 mm×1 500 mm,恒载取2.0 kN·m-2,活载取3.5 kN·m-2。分别考虑集中人群和分布人群下人体阻尼对结构产生的响应,计算结果如图8所示。
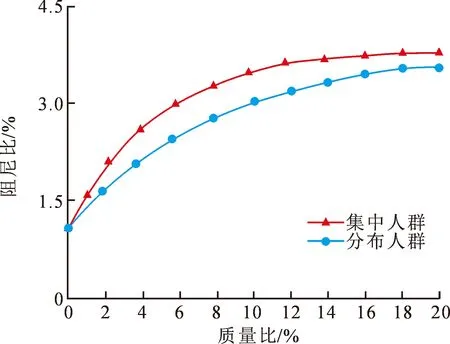
图8 人对结构阻尼比的影响
图8表明,将人群等效为集中荷载和分布荷载分别施加于跨中时,其质量比和阻尼比的变化趋势基本相同。在质量比为20%的情况下,与原结构相比,集中人群和分布人群的阻尼比分别增加了2.52倍和2.30倍。这就说明人群分布离振幅最大处的距离越近,对结构的阻尼效果贡献越大;相反,人群分布越分散,离最大振幅处越远,则对结构的阻尼效果贡献越小。可见,人群有增大结构振动阻尼的作用,然而在进行舒适度分析时,通常被忽略,因此得到的结果偏于保守。
3.5 TMD 设计参数与大跨度连廊减振分析
由前述分析可知,叠层连廊的1阶竖向自振频率为4.29 Hz。当步频为1.4 Hz和1.5 Hz时,步频的3阶荷载分量接近4.29 Hz,与1阶竖向振动模态形成共振,加速度峰值超限值要求,因此,需要控制4.29 Hz处的振动响应。在14 m标高处连廊跨中外侧节点下部布置减振装置,位置如图9所示。连廊1阶竖向4.29 Hz振型的参与质量为M=371 587 kg,取TMD质量为1 t,设计参数见表4。

图9 叠层连廊TMD减振器布置位置

表4 TMD 设计参数
图10和图11分别为1.4 Hz和1.5 Hz下加速度时程曲线及加速度峰值曲线。相比于原结构步频1.4 Hz时的峰值加速度0.242 m·s-2,放置TMD后的峰值加速度降低至0.124 m·s-2,减振率为49%,减振效果明显,满足舒适度标准要求。但对于步频1.5 Hz时的峰值加速度仅降低了10%,减振后加速度依旧不满足限值要求,因此需要对减振器的布置进行优化设计。
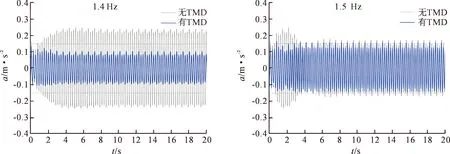
图10 TMD减振结构加速度时程曲线
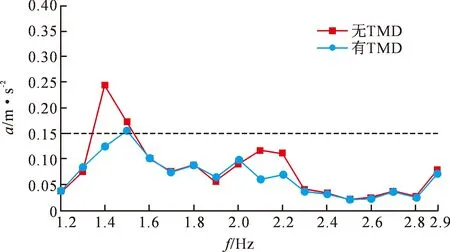
图11 结构自振峰值加速度对比
3.6 连廊优化设计
考虑到结构自振峰值加速度变化对结构自振特性产生的不利影响,设置2个不同调谐频率的TMD来扩大减振频带宽度,以确保减振的可靠性。TMD布置位置如图12所示,参数见表5。
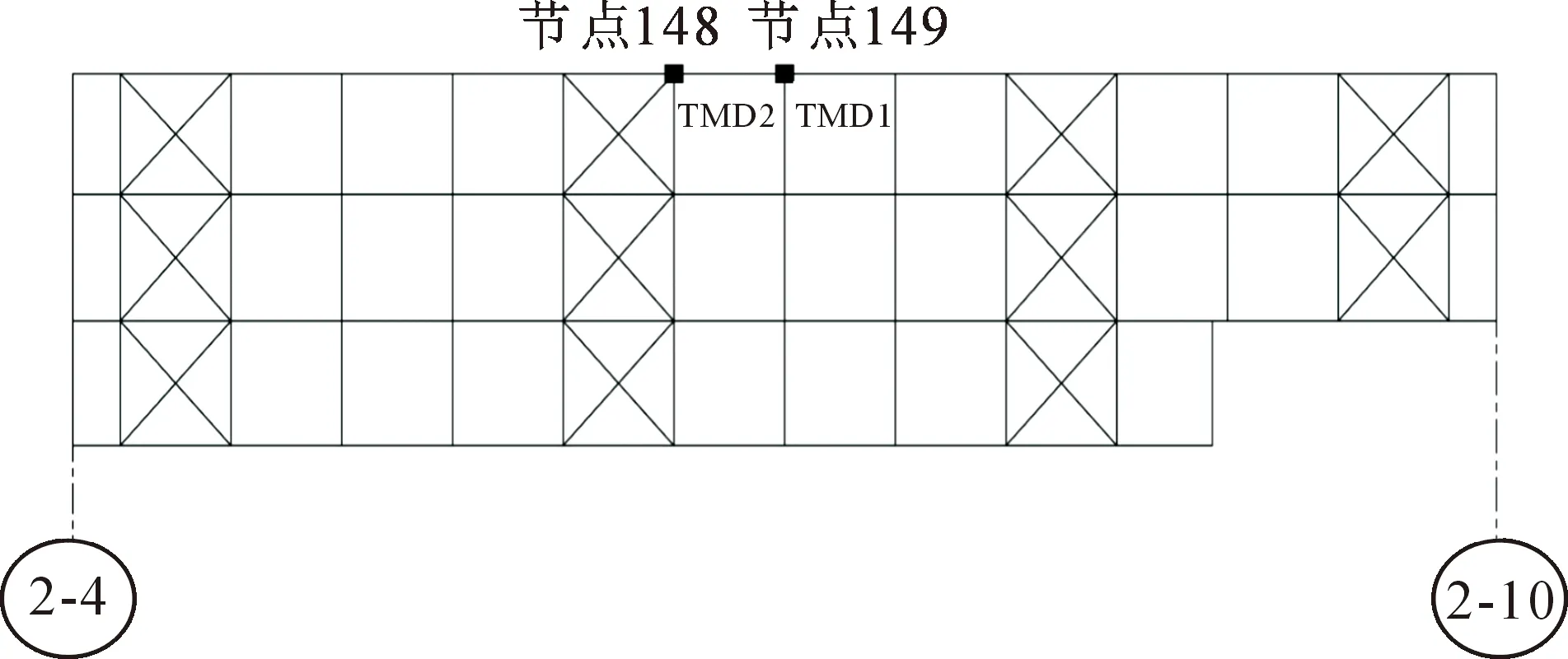
图12 叠层连廊TMD减振器布置位置

表5 TMD2设计参数
各工况下最大位移节点加速度峰值如图13所示。与原结构相比,增设调谐4.5 Hz的TMD有助于扩大减振的频带宽度,有效降低频率点处的加速度响应。步频1.4 Hz时的峰值加速度为0.101 m·s-2,减振率为58%,相比于单频率TMD提高了9%。同时,步频1.5 Hz时的峰值加速度为0.112 m·s-2,减振率为35%,相比于单频率TMD提高了25%。峰值加速度和减振率见表6。

表6 不同减振方案下减振效果对比
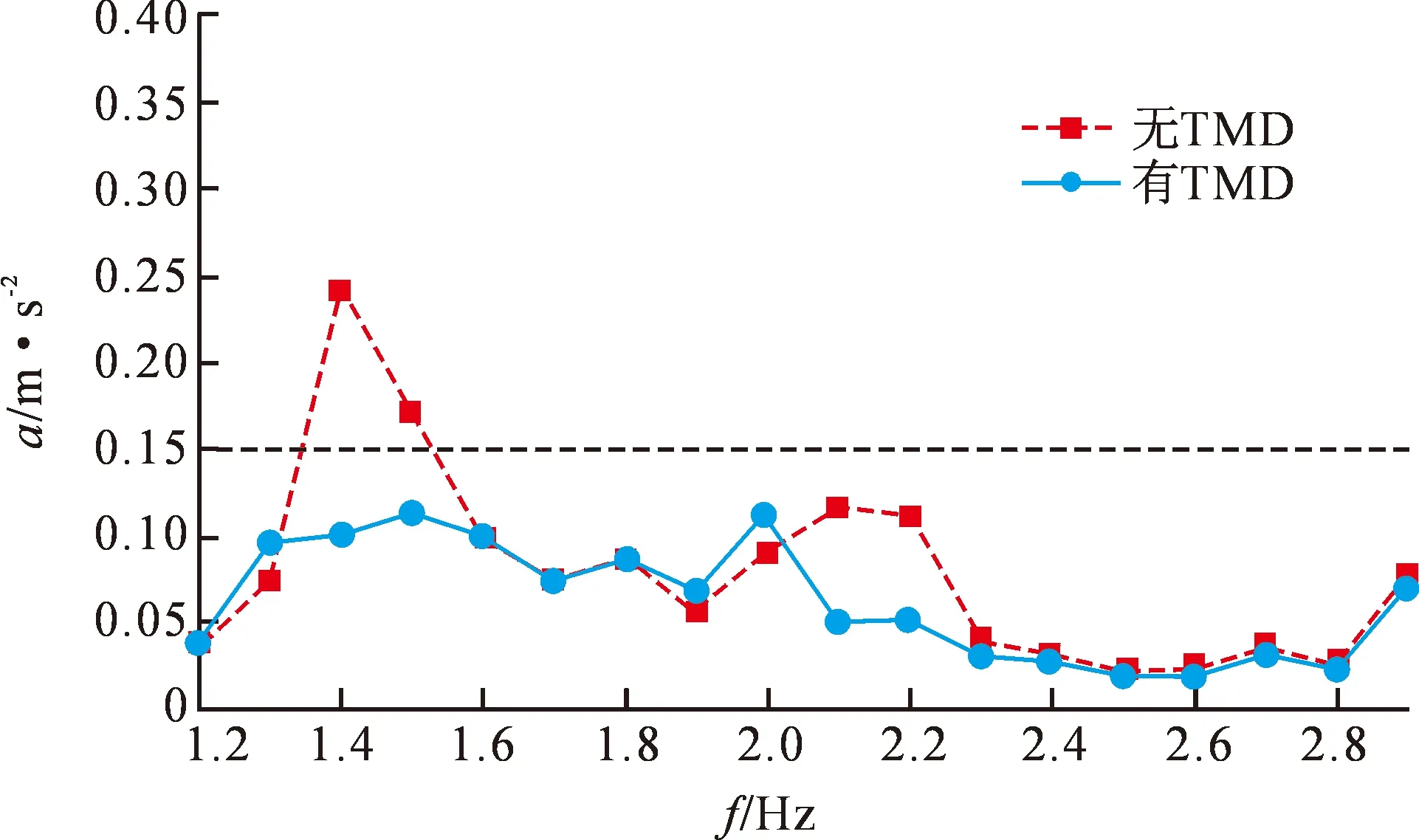
图13 多频TMD放置前后结构自振峰值加速度对比
优化结果表明:布置多个不同频率的TMD对周围频率点处的减振效果优于单个TMD,同时,减振效果更为明显,舒适度满足设计要求。
4 结 论
1) 文中利用Ritz向量法对大跨度叠层连廊结构进行模态和步行振动响应分析,建立了叠层桁架的空间有限元模型,采用TMD进行竖向舒适度控制,并分析了连廊振动响应的影响因素。
2) 对大跨度连廊舒适度评价标准,引入了加速度限值要求。当板厚由80mm增大到180 mm时,其自振频率下降了1.8%,峰值加速度下降了36.9%,板厚对结构频率的影响小于对峰值加速度的影响。在集中人群和分布人群荷载工况下连廊结构的阻尼比是原结构的2.52倍和2.30倍,对减小振动时的加速度有一定的贡献,一般结构分析时不考虑这一点得到的结果偏保守。
3) 布置多频率TMD后连廊结构步频为1.4 Hz和1.5Hz的峰值加速度,相比于原结构的减振率分别为为58%和35%,相比于单频率TMD的峰值加速度的减震率提高了9%和25%。采用多频率TMD能够有效扩大减振的频带宽度,降低加速度响应,从而满足舒适度要求。TMD不同的设置位置对结构减震效果的影响有待进一步研究。

