大跨复杂斜柱钢框架施工全过程的模拟分析*
梁 岩 魏莹莹 冯浩琪 赵 明 郭 靖
(1.郑州大学土木工程学院,郑州 450001;2.中国联合工程有限公司,杭州 310000)
大跨钢结构具有跨越能力强、承载力高及结构美观等优点,在公共与工业建筑中广为应用[1]。但其体量庞大、结构复杂、设计难度大,施工具有时变性[2],这就要求对结构施工过程进行有限元模拟分析及监控,确保施工方案的科学性及施工过程的安全性。秦杰等对奥运会羽毛球馆预应力和变形施工监测做了研究,借助有限元软件进行分析对比验证了有限元模拟分析的正确性与准确性,保障了施工质量和安全[3];王秀丽等对西宁体育馆钢结构屋盖进行了施工加载过程有限元模拟分析与健康监测,较好地反映了结构内力变化与受力形态[4];田黎敏等采用施工力学方法对三个大跨度复杂钢结构工程进行施工过程跟踪模拟分析,表明进行施工过程模拟分析可以优化施工方案,保证施工过程中结构的安全[5];吴穷等对武汉光谷网球中心进行施工监测,将计算值与监测值对比分析,两者基本能吻合,结果表明结构的最不利状态有可能出现在施工过程中[6]。在这些研究中,针对施工过程监控的分析多为上部屋架钢结构,而对大跨钢结构下部支承系统及基础关键部位的研究甚少。以某遗址保护工程大跨斜撑钢结构建筑为依托,采用有限元分析软件MIDAS/Gen对应天门城楼施工过程进行了模拟,得到结构施工过程中斜柱支承系统构件内力及桩顶位移变化规律,并与相应测点实测数据对比;同时针对实际施工过程中的异常情况及时作出预警,以保证正常施工的安全。
1 工程概况
应天门遗址保护工程(图1)采用对遗址进行全覆盖模式,工程分为三个部分,分别是东西对称的阙楼、朵楼和位于中间位置的城楼。研究主体为城楼。城楼建筑主体设计为地上9层,建筑总高约46 m。城楼主体采用钢结构,在立面上分为8.22 m以下的斜柱支承结构、24.27 m以下的大跨度桁架转换层结构和上部钢框架结构。

图1 应天门遗址建筑立面Fig.1 The facade of the building in Yingtianmen Site
为避免上部结构施工过程中对既有遗址的不利影响,上部荷载通过大跨度转换结构传递到遗址外围桩基础承台上,下部遗址层支承斜柱与地面斜交约60°,水平分力明显(图2)。为平衡斜柱柱脚水平推力,通过在基础承台之间暗挖顶管预应力拉杆,使结构平面上处于自平衡状态,遗址区域能得到很好的保护[7]。基础预应力钢绞线张拉与上部结构施工存在多次平衡转换,桩基在上部水平荷载及基础预应力荷载作用下会产生水平位移,该位移过大将引起桩身开裂,影响结构安全。因此在预应力施工过程中需严格控制桩顶位移和斜柱应力。
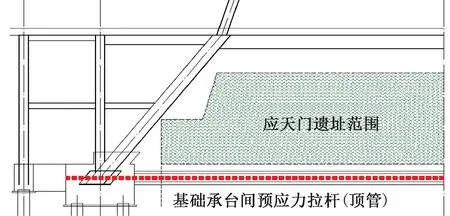
图2 下部斜柱支承系统Fig.2 The support system of inclined pillars in the lower part of the building
2 测点布置及有限元模型建立
2.1 测点布置
为保证上部结构施工过程中基础的安全性,在暗挖顶管处需设置测点,测点处布置振弦式应变计,以分析顶管梁受力状态;在承台处需设置位移测点,测点处分别安装百分表,用于测量承台顶部水平位移,并以此推算桩顶水平位移(规定承台位移向外为正)。下部结构施工监测(图3)包含:承台位移、顶管轴力、基础承台沉降。

1—承台;2—预应力拉杆。图3 承台及拉杆测点布置Fig.3 Arrangements of measurment points on caps and pipe jacking
在上部钢结构中,斜钢柱作为整个结构的主要支承构件,其柱端由于受轴力和弯矩的双重作用,压应力较大,因此需要在斜柱关键部位设置测点,埋设振弦式应变计,用于获取施工中关键部位应力及其变化规律。斜柱支承系统施工监测(图4)包含:柱脚应力、斜柱轴力应力、柱顶位移。斜柱应力与基础承台位移测试相互验证,形成闭合数据分析链。
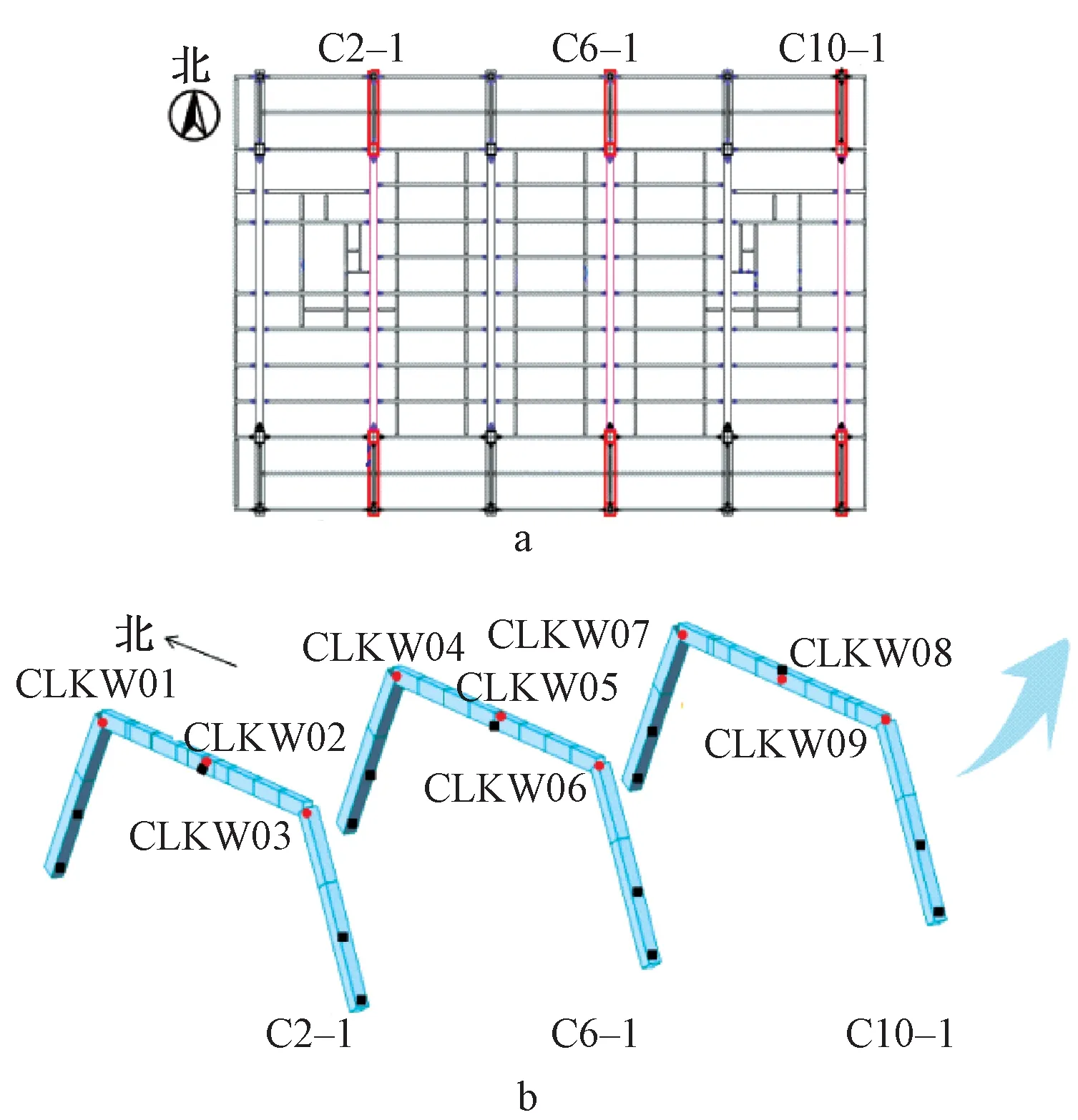
a—底层框架平面布置;b—部分斜柱框架。 位移测点; 应力测点。图4 斜柱支承框架测点布置Fig.4 Arrangements of measurement points on the moment frame with inclined pillars
2.2 有限元模型建立
在有限元分析软件MIDAS/Gen中建立城楼模型。由于城楼理论模型分析计算量大、复杂程度高,需要根据工程实际情况进行模型简化。城楼上部钢结构构件采用梁单元模拟,下部基础承台采用实体单元模拟,各层楼板及屋面、挑檐钢板选用板单元进行模拟。构件之间的连接采用共节点(刚接)。
根据应天门遗址保护工程单桩水平静载试验结果(表1)可知:编号SZ-70-02及SZ-70-03试桩水平临界荷载280 kN对应的水平位移分别为2.00,8.85 mm,因此桩顶水平位移容许值取2 mm,桩顶水平刚度取30 kN/mm。同时考虑水平弹性支撑刚度KH,约束竖向位移及转动,桩土相互作用采用等效的节点弹性支承模拟[8]。将桩简化为节点弹性支承作为边界条件。
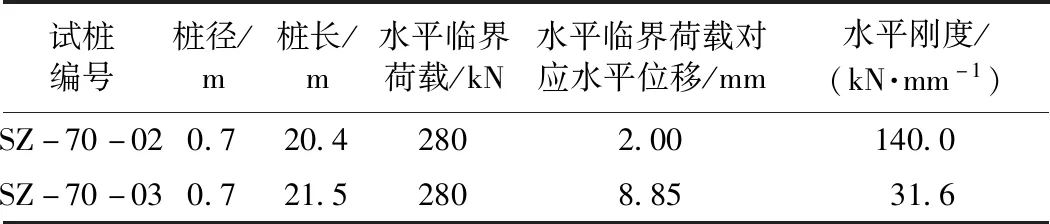
表1 单桩水平静载试验结果Table 1 Horizontal static test results of single pillars
各钢梁、钢柱截面形式根据设计图纸采用自定义截面法确定,通过定义有限元模型中单元转角的方法确定钢梁单元横截面朝向。施工阶段模拟通过结构组、边界组和荷载组的激活或钝化实现。城楼有限元模型如图5所示。
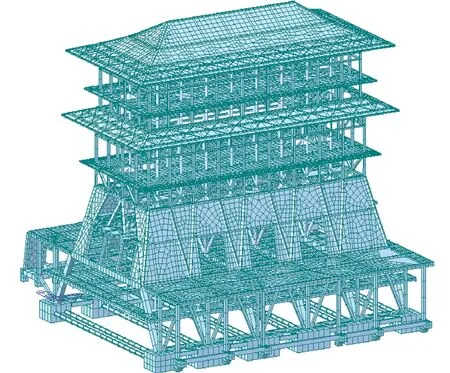
图5 城楼有限元模型Fig.5 The finite element model of the city gate tower
根据施工条件及施工工艺,综合考虑各种因素后,偏安全地分三阶段张拉,施工阶段初步划分如表2所示。

表2 施工阶段初步划分Table 2 Preliminary division of construction phases
3 模型优化及施工阶段调整
有限元模拟分析时,一方面,模型部分参数与现场实际情况有差异,因此,需要对施工中部分数据进行采集,并与理论数据进行对比分析,对模型进行优化,使其更加接近现场实际施工情况,并指导后续施工[9-10]。另一方面,部分施工设计未达到最优施工工序,需要根据调整后的最优工序进行实际施工。
3.1 模型优化
阙楼与城楼的张拉方案具有相似性,实际施工是以阙楼第一次预应力张拉完成的监测数据为指导。根据阙楼前期实际监测结果,在第一次预应力张拉后,承台向内实际位移小于理论计算值。因原模型仅考虑桩基对承台的约束作用,忽略承台周围回填土及遗址堆载对承台的抗力作用,导致承台水平位移监测值与理论值存在较大误差。因此,结合阙楼第一次预应力张拉完成后的分析结果调整城楼有限元模型中基础部分边界条件。如图6所示,在原模型的基础上,考虑上部遗址原土堆载高度5 m,土的重度根据地勘土层信息报告取18 kN/m3,根据Rankine土压力理论将遗址土等效为大面积均布荷载,承台高度范围内回填土等效为三角形土压力,并将土压力加载到承台侧面。
3.2 实际施工阶段调整
在预应力张拉过程中,由于现场情况多变,工程设计和现场施工条件存在很大差异,为减少断丝、滑丝等现象发生,结合阙楼初次张拉承台位移离预期较小,同时为了减小施工步骤,缩短施工工期,施工中将城楼预应力张拉方案调整为分两次张拉。
图7为城楼两种张拉方案承台CLWY08测点的位移对比。对于三阶段张拉方案,第一次张拉完成后,承台位于初始位置附近,随着施工进行,上部荷载逐渐增大,承台产生正向位移,且位移逐渐增大;第二及第三次张拉完成后,承台产生明显的负向位移;使用阶段承台位移为-1.13 mm。当采用两阶段张拉方案时,第一次张拉完成后,承台位移为负,随着施工的进行,上部荷载逐渐增大,承台位移向正方向移动,逐渐到达初始位置;第二次张拉完成后,承台产生负方向位移;使用阶段承台位移为-1.02 mm。两种张拉方案中承台位移相差不大,且分两次张拉更接近初始位置。
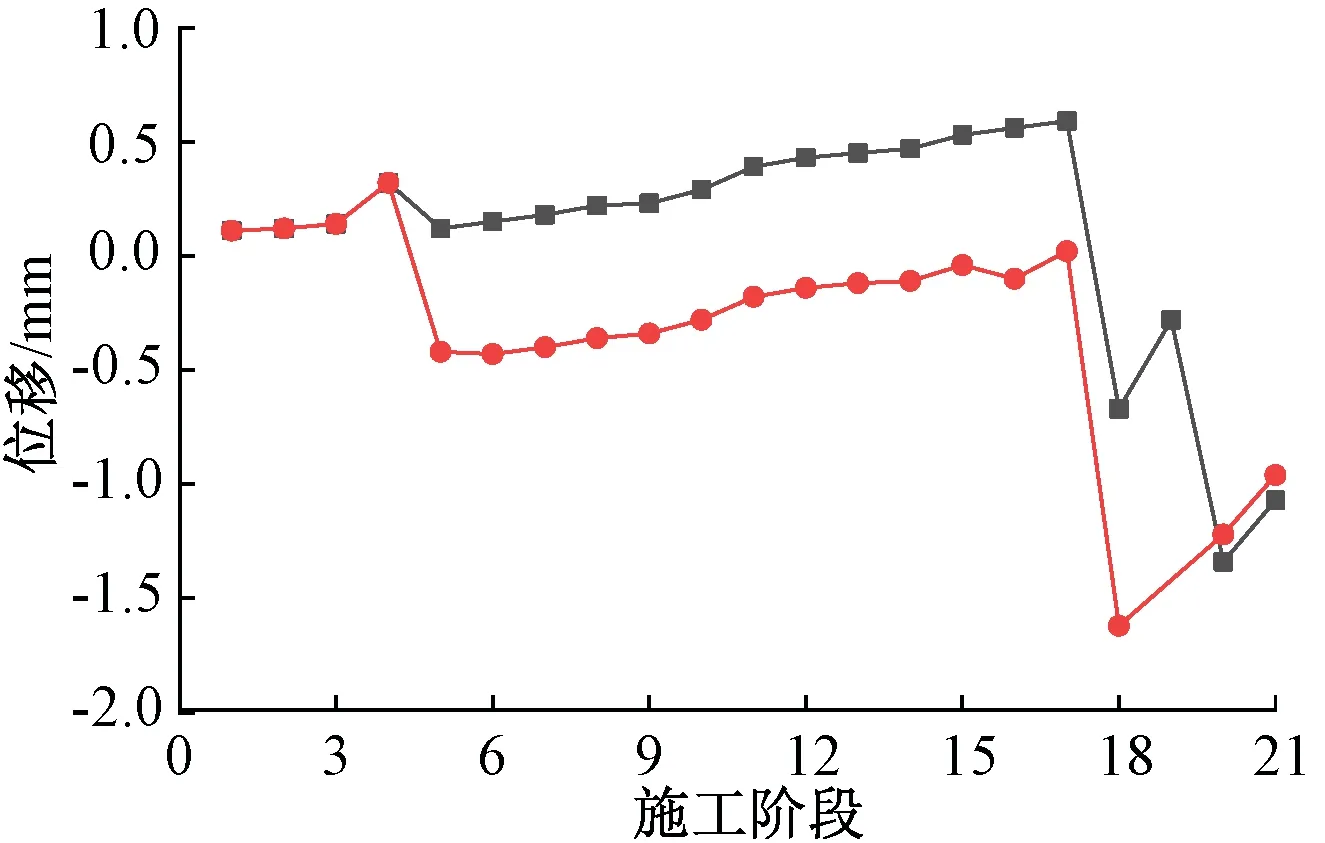
三次张拉;两次张拉。图7 承台CLWY08测点位移对比Fig.7 Comparisons of the displacement at measurement point of cap CLWY08
在施工过程中,根据现场实际条件及上述分析结果,采用了两次张拉方案并调整了部分施工阶段,实际施工阶段划分如表3所示。

表3 实际施工阶段划分Table 3 Division of the actual construction phases
4 模拟值与实测值对比分析
由于篇幅限制,选取C10-1框架柱测点、DGL-3400(东)顶管梁测点、CLWY08承台测点为研究对象,根据现场实测数据与模型理论数据进行对比分析。
4.1 应力分析
有限元模型使用阶段的应力如图8所示。
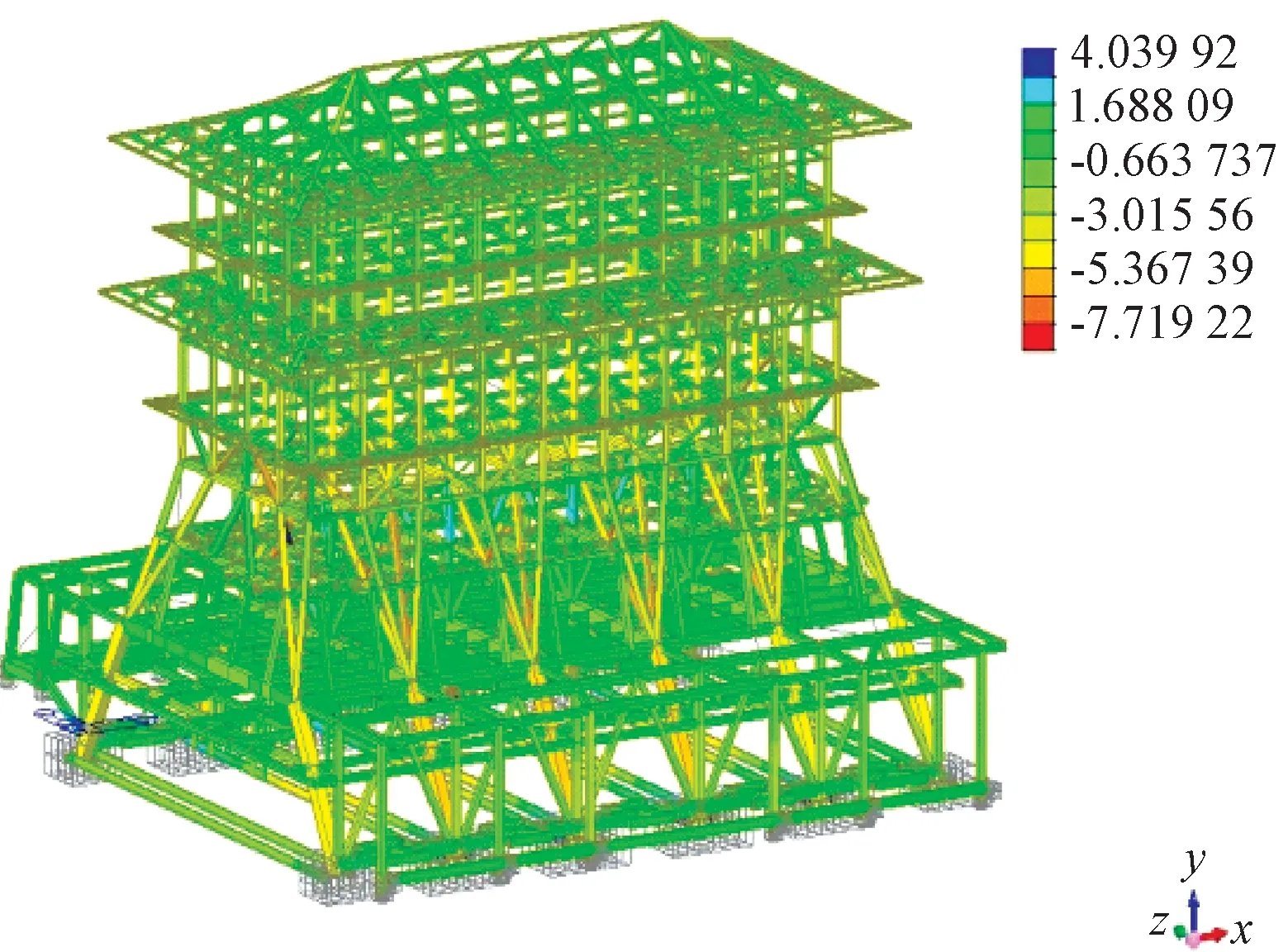
图8 结构使用阶段应力 MPaFig.8 Contours of stress of the city gate tower in the service stage
图9为框架C10-1斜柱的应力变化曲线,斜柱各点应力实测值与理论值变化趋势基本一致。阶段14第二次预应力张拉阶段,在预应力及部分装饰装修荷载作用下,斜柱应力发生明显突变。阶段15装饰装修完成,在弯矩和轴力共同作用下,斜柱应力增大。施工完成后,实测应力和理论应力存在差异,理论应力最大为-8 MPa,实测应力为-9.3 MPa。

模拟值;实测值。图9 C10-1框架南侧斜柱应力变化Fig.9 Variations of the stress of the inclined pillar in the south side of frame C10-1
由图10可知,梁跨中应力变化十分复杂,梁为受弯构件,由轴力产生的弯曲应力较小,弯矩引起应力为主控因素。前三个施工阶段,框架梁临时支撑未卸载,上部荷载作用下梁跨中应力为拉应力,变化平缓。阶段4临时支撑卸载后,拉应力突变为压应力;随着上部荷载的增加,梁跨中应力逐渐增大。施工完成后,框架梁跨中压应力实测值达到最大值-37.6 MPa,对应理论值为-27.4 MPa。

模拟值;实测值。图10 C10-1框架梁跨中应力变化Fig.10 Variations of stress at the midspan of frame beam C10-1
图11为C10-1框架南侧柱脚应力变化情况,可知:柱脚各点实测值与理论值变化趋势基本一致;斜柱作为压弯构件,前期施工中弯曲应力起控制作用,柱脚外侧受压、内侧受拉;在阶段13前,随着施工进行,上部荷载逐渐增大,轴向应力逐渐起控制作用,柱脚转变为全截面受压;阶段14,由于预应力张拉,柱脚外侧应力突然增大,柱脚内侧由压应力变为拉应力;阶段15柱脚各点应力逐渐增大,由于装饰装修完成,框架轴力和弯矩增大,在轴力和弯矩的共同作用下,框架各点应力变大;施工完成后,柱脚外侧理论应力最大为-72.1 MPa,实测应力最大为-61.2 MPa,柱脚内侧理论应力最大为21.4 MPa,实测应力最大为18.8 MPa。
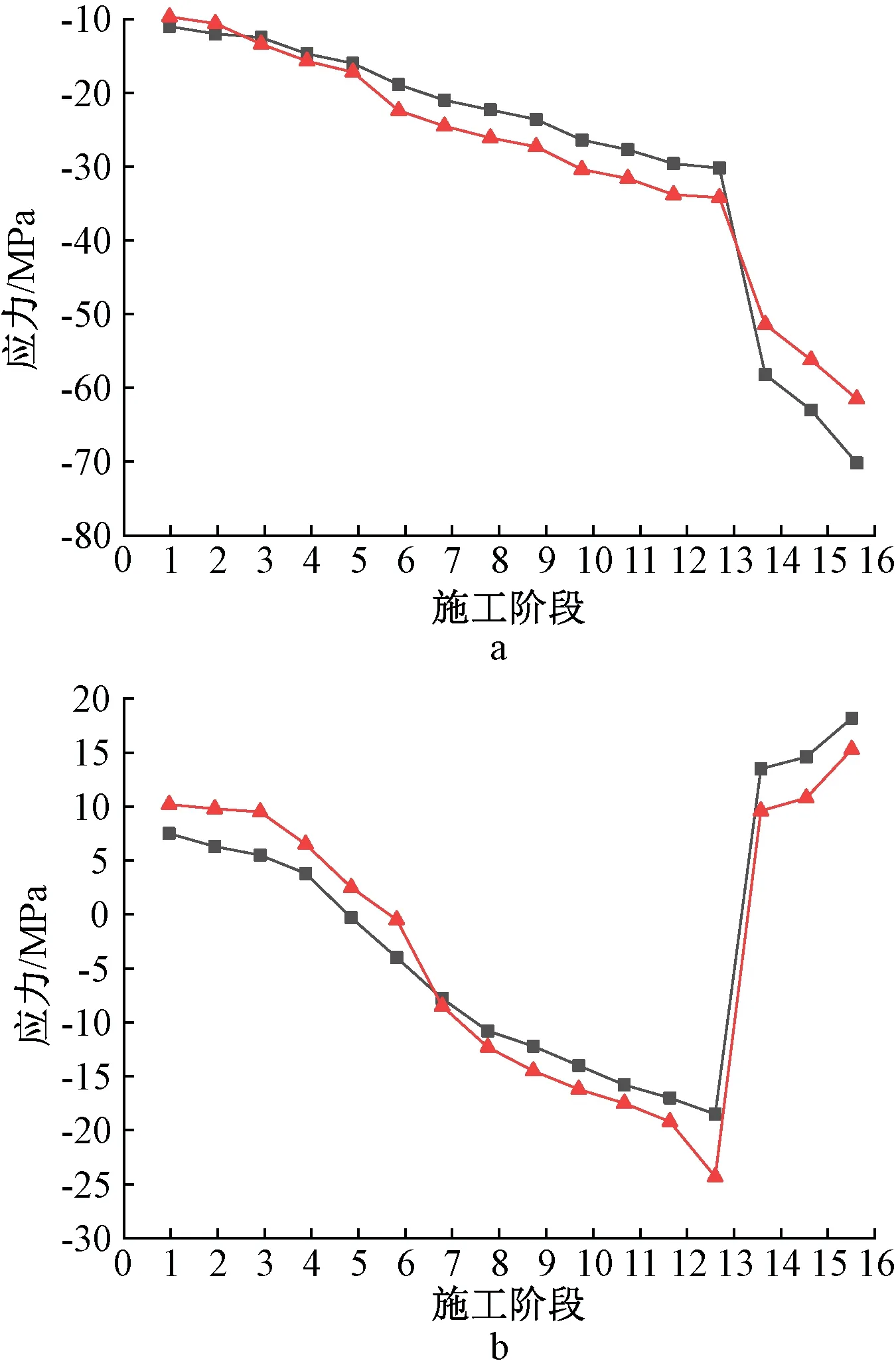
a—柱脚外侧应力;b—柱脚内侧应力。模拟值;实测值。图11 C10-1框架南侧柱脚应力变化Fig.11 Variations of stress at the column foot in the south side of frame C10-1
图12为DGL-3400(东)顶管梁应力变化情况,可知,理论值与实测值变化趋势一致。第一次张拉前监测顶管处于受拉状态,预应力张拉后监测顶管处于受压状态,之后随着上部结构施工,柱脚水平分力逐渐增大,顶管逐渐由受压状态向受拉状态过渡;在第二次张拉完成后,顶管从受拉状态转变为受压状态,且顶管应力达到最大值,实测最大值为-17.1 MPa,对应模型理论值为-25.6 MPa。

模拟值;实测值。图12 DGL-3400(东)顶管梁应力变化Fig.12 Variations of the stress of pipe jacking DGL-3400
对施工中结构底部的斜柱支承体系力学性能进行分析,结果表明各构件关键截面应力均在容许范围之内,结构受力较为合理且强度满足要求。
4.2 位移分析
有限元模型结构使用阶段位移如图13所示。
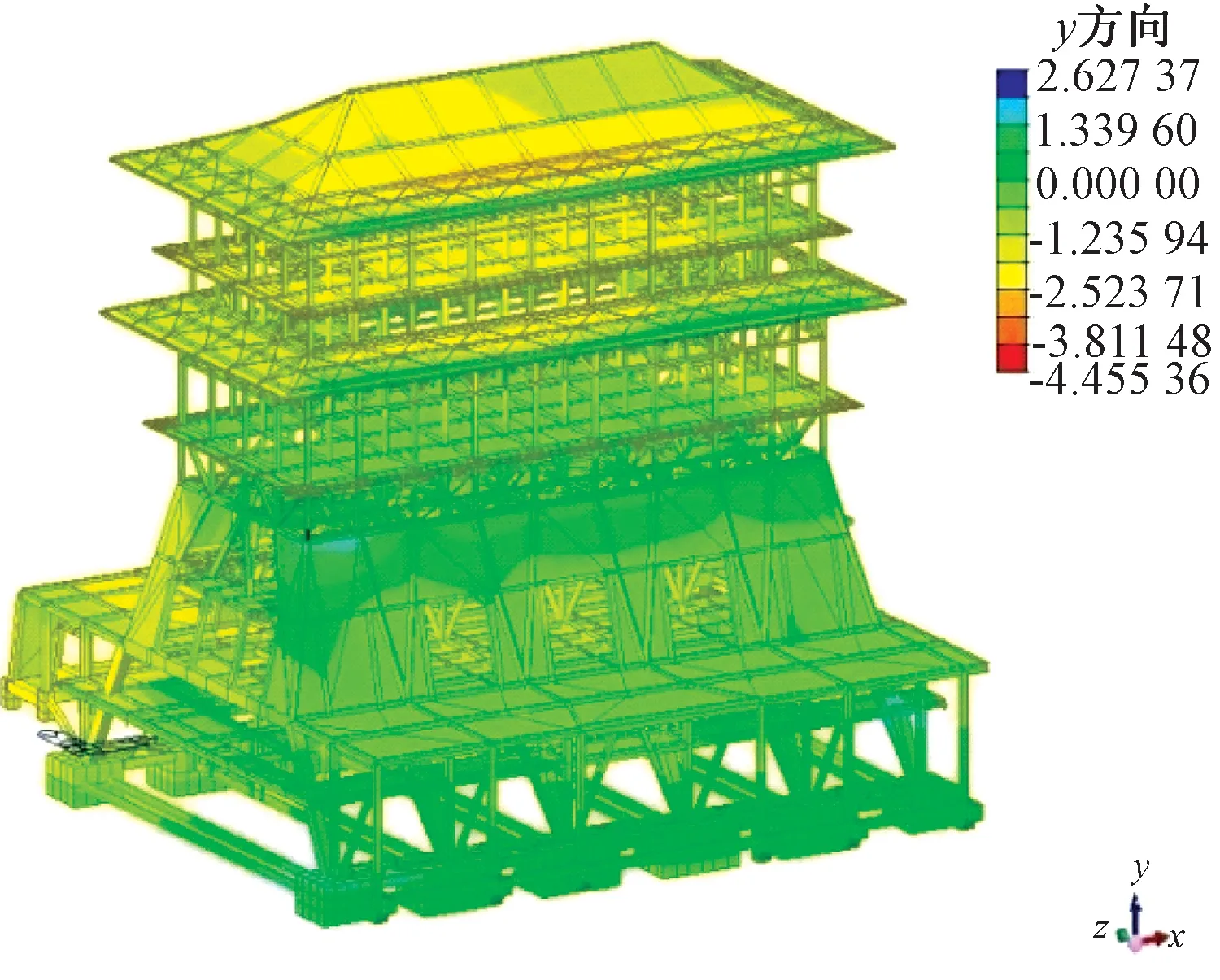
图13 结构使用阶段位移 mmFig.13 Displacement of the city gate tower in the servic stage
根据图14可知:结构在重力作用下桩顶产生正向位移,预应力张拉引起桩顶位移向预应力施加方向变化;随着上部结构施工,荷载逐渐增大,桩顶又产生正向位移;第二次预应力张拉后,桩顶位移达到最大值,为1.42 mm,小于设计控制值2 mm,结构位移在可控范围内;在装饰装修及使用阶段,桩顶位移产生正向相对移动但仍未回到原始位置。

图14 承台CLWY08测点处桩顶位移变化Fig.14 Variations of the displacement on the pile top at the measurement point of cap CLWY08
图15为承台CLWY08测点实测及理论位移值,可知:承台位移变化趋势与桩顶位移变化趋势保持一致,且现场实测值与理论值变化趋势较为接近,但实测值小于理论值,表明结构基础实际刚度略大于有限元模型基础刚度。实测位移最大值为0.9 mm,理论位移最大值为1.41 mm,小于设计控制值2 mm。
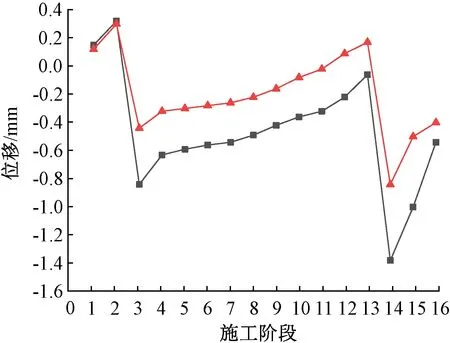
模拟值;实测值。图15 承台CLWY08测点位移变化Fig.15 Variations of the displacement at measurement points of cap CLWY08
通过上述对监测结果的分析,再结合桩顶水平位移的理论分析结果,可以推断在整个施工过程中桩顶水平位移也较小,桩身没有发生剪切破坏的趋势和迹象,因此整个施工过程中桩身处于安全状态,说明两阶段张拉方案比较合理且能够保证结构施工过程的安全性。
通过以上对比可知,现场实测值与理论值存在差异,造成两者差异原因主要有:建模时不可避免地存在模型的简化,如柱脚、顶管梁、承台三者连接的简化,结构各杆件之间的连接等;结构理论模型与实际结构施工环境存在差异,建模参数设置存在误差,如施工工艺及顺序、材料的不均匀性,荷载组合等;有限元理论本身存在误差,与实际构件相比存在离散化误差。
5 结束语
1)施工过程中斜柱支承系统各构件关键截面应力均在容许范围之内,且实测值和理论值变化趋势基本一致,结构受力较为合理且强度满足要求。
2)承台位移变化趋势与桩顶位移变化趋势保持一致,且实测值与理论值变化趋势较为接近。承台位移实测最大值为0.9 mm,理论最大值为1.41 mm,小于设计控制值2 mm,桩身处于安全状态,两阶段张拉方案比较合理且能够保证结构施工过程的安全性。
3)考虑遗址原土堆载的桩的简化模型一定程度上能反映斜柱支承系统构件内力及桩顶位移变化规律,具有一定的实用性。

