一种改进两步加权最小二乘的TDOA定位算法*

孟天次，张贞凯，林云航

(江苏科技大学 海洋学院，江苏 镇江 212028)

0 引 言

水下声源定位技术作为现代研究的热点技术之一，被广泛应用于信号处理、无线传感网等领域[1-2]。现有的水下定位方法包含到达时间(Time of Arrival,TOA)、到达角度(Angle of Arrival,AOA)、到达时间差(Time Difference of Arrival，TDOA)、接收信号强度(Received Signal Strength,RSS)等[3-4]。TOA定位方法需要传感器与被定位目标之间保持精确的时间同步，但实际定位过程中很难保证两者之间的时间同步，所产生的较大误差导致定位精度下降。TDOA定位方法只需要保持传感器之间的时间同步而不考虑声源发射声波的初始时刻，相比于TOA定位精度有所提高，故本文主要针对TDOA算法进行研究。

TDOA定位方法是一种经典的测距技术，主要通过测量目标源到达不同传感器的时间差来获得距离差，通常采用三个不同的传感器可以测得两个TDOA，目标源点位于两个TDOA决定的双曲线焦点上[5]。常用的定位算法包括Chan氏算法、Taylor算法以及两步加权最小二乘(Two-Stage Weighted Least Squares，TSWLS)算法。文献[6]中的Chan氏算法只有在测距误差较小的情况下才能获得较好的定位结果，但实际的水声信道是多径、时变的[7]，测距过程会产生较大的误差值，导致定位精度下降。文献[8]中的Taylor算法则是一种循环迭代的递归算法，相比于Chan氏算法具有良好的估计性能。但其在迭代计算中需要一个初始值，当选取的初值偏离目标真实值较大时，定位精度必将受到影响，导致定位结果变差。为了克服以上两种算法的缺点，文献[9]提出了两步加权最小二乘算法。该算法分为两步，首先利用加权最小二乘(Weighted Least Squares，WLS)算法初步估计出目标位置；随后引入目标位置误差修正初步估计值，提高了定位精度。由于该算法是闭式解，故不存在收敛问题，但其因平方以及开方等非线性运算，致使计算过程中均忽略了二阶误差项，当测距误差较大时定位精度有所下降。

文献[10]提出了一种改进的两步加权最小二乘(Improved Two-Stage Weighted Least Squares，ITSWLS)算法，通过对中间变量进行两次泰勒展开，避免了二阶误差项的引入，获得了更高的定位精度。但两次泰勒展开均忽略了展开的高阶项，一定程度上会影响算法的定位性能。在此基础上，本文提出了一种改进算法。首先引入时差方程，构建新的定位方程，利用加权最小二乘算法初步估计目标位置，有效避免了平方过程忽略的二阶误差项；接着引入中间变量并进行泰勒展开，利用中间变量与目标位置误差之间的非线性函数关系构建定位方程，对目标位置初步估计值进行校正，同样也避免了二阶误差项的丢失，最终得到更加精确的目标位置估计值。

1 定位模型

根据上述定义，声源与第i个传感器的距离为

(1)

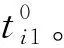
(2)

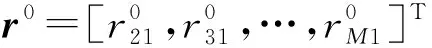
2 改进算法

为了解决TSWLS算法在第一步和第二步因平方以及开方等非线性运算丢失平方的二阶误差项的问题，本文在原算法的基础上引入时差方程，避免了二阶误差项的丢失，一定程度上提高了算法的抗噪声性能。接下来给出改进算法的详细推导过程。

2.1 初步估计

(3)

式(3)可以改写为

(4)

将式(2)时差方程代入式(4)可得

(5)

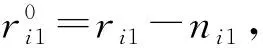
(6)

将式(6)表示为向量形式：

h1-A1θ1=B1n=ε1。

(7)

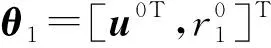
(8)

(9)

(10)

与传统TSWLS不同的是，对于式(3)，本文并没有采取对(ri1-ni1)进行平方，而是采取式(4)的计算方式并引入时差方程，避免了因平方而引入的二阶误差项。对式(7)利用加权最小二乘可得声源位置初步估计值为

(11)

加权矩阵W1=E[ε1ε1T]-1，由(7)式可得

W1=E[B1nnTB1T]-1=(B1QnB1T)-1。

(12)

(A1TW1A1)-1A1TW1ε1。

(13)

(14)

2.2 修正初步估计值

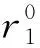
(15)

(16)

已知Δθ1的均值近似为零，故Δu的均值也近似为零，则有

03×1=Δu-Δu。

(17)

结合式(16)、(17)可得

h2-A2Δu=B2Δθ1=ε2。

(18)

式中：ε2为噪声误差项，

(19)

(20)

(21)

对式(18)利用加权最小二乘可得声源位置误差Δu估计值为

(22)

式中：加权矩阵W2=E[ε2ε2T]-1。由式(14)、(18)可得

W2=E[B2Δθ1Δθ1TB2T]-1=

(23)

(24)

综上所述，本文所提算法计算流程如下：

3 CRLB分析

(25)

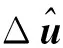
(26)

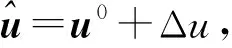
(27)

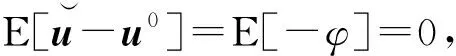
(28)

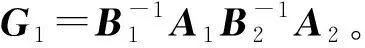
由文献[11]和文献[13]可知，TDOA定位的CRLB矩阵可以表示为

(29)

(30)

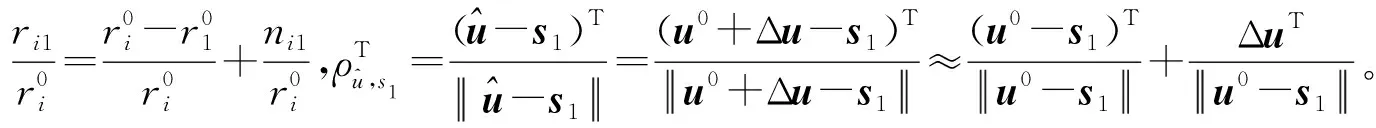
(31)

因此，可以说明本文算法的定位精度在噪声较小的情况下可以达到CRLB，其可以表示为

CRLB=trace{(J-1)}。

(32)

4 仿真结果与分析

对于水下三维定位场景，为了提高定位精度，获得更加精确的估计结果，需保证式(7)为非欠定方程[14]，即传感器的个数需满足(M-1)≥(3+1)。考虑实际应用问题，本文选取M=5个传感器，其位置分别为s1=[200,250,150]T，s2=[300,0,500]T，s3=[0,400,800]T，s4=[-300,0,500]T，s5=[0,-400,200]T，单位均为m。其中s1为参考传感器的坐标位置。已知TDOA测量向量r的协方差矩阵为E[nnT]=Qn，本文假设Qn=σ2ρ，其中σ2为TDOA测量噪声的方差，ρ是对角线元素为1、其余元素均为0.5的(M-1)×(M-1)维矩阵。

(33)

(34)

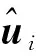
根据目标距离传感器位置的远近分为近场目标和远场目标，并分别对其进行仿真，仿真前设声源的真实位置分别为u0=[200,300,400]Tm，u0=[20,30,120]Tm。仿真过程中不断改变测距误差大小，比较三种不同算法的定位精度。

4.1 近场目标仿真

由图1可知，当测距误差低于0.01 m时，各算法都趋近于克拉美罗下界，定位精度相对较高，然而随着测距误差的增加，各算法逐渐偏离CRLB，当测距误差为10 m时，所提算法的定位误差相比于Chan算法和文献[10]算法分别减少了42.25 m和4.84 m，算法整体的定位精度分别提高了36.9%和4.7%。这是因为Chan算法和文献[10]算法在计算过程中均有高阶项的丢失，随着误差的增大，对其定位性能有一定的影响，导致两种算法的定位精度下降。

图1 近场目标各算法的RMSE对比图

从图2中可以看出，相比于其他两种算法，随着测距误差的增加，本文所提算法的偏差最小，抗噪声性能最好。

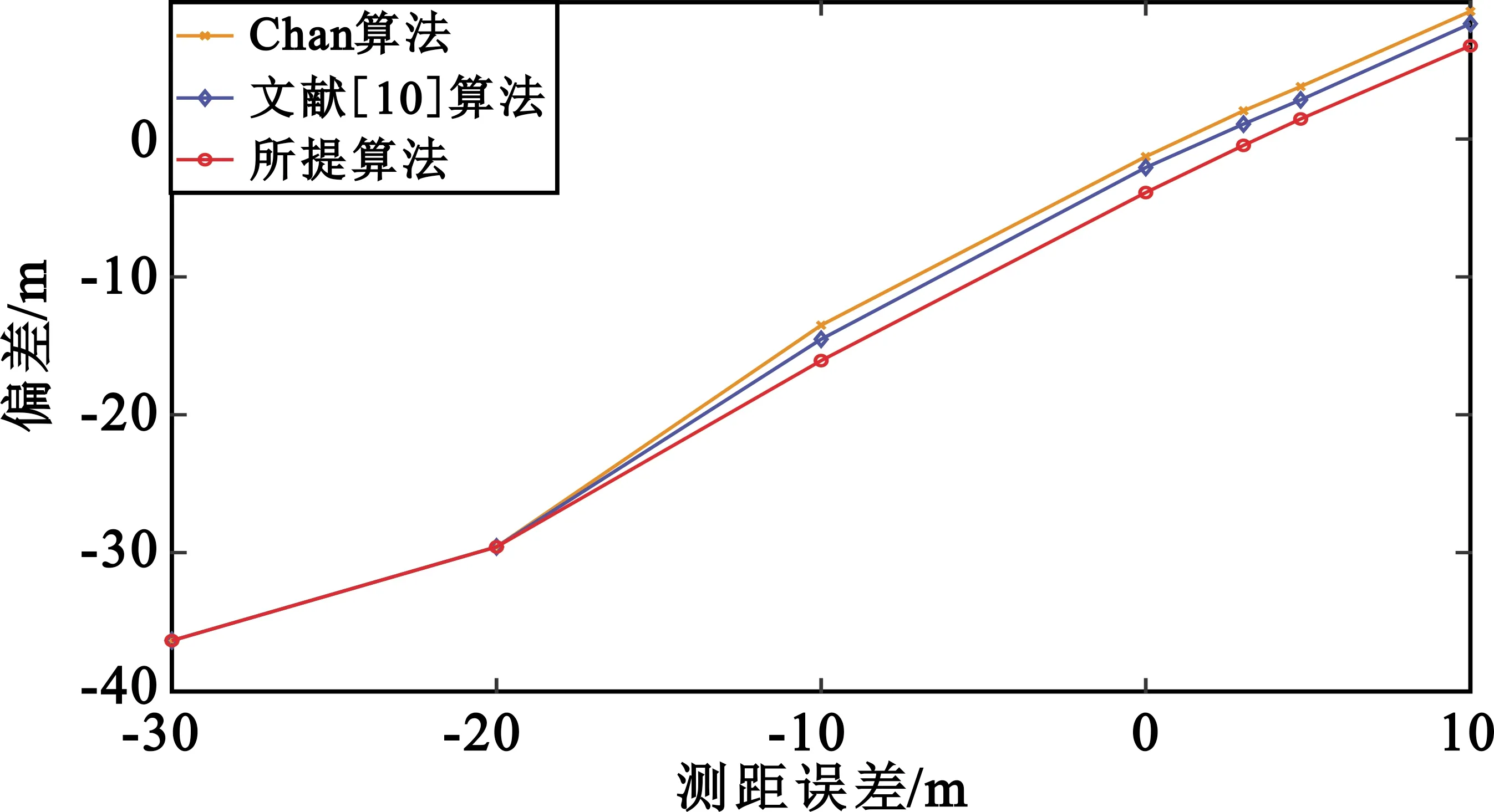
图2 近场目标各算法的偏差对比图

CDF是在某一个门限误差下，算法定位误差低于门限误差的次数占仿真总次数的比例。图中曲线上升的趋势越快，表示低于门限误差的次数越多，定位性能越好。图3为测距误差为1 m时，各算法的CDF曲线图。由图3可知，所提算法曲线上升最快，表明本文所提算法要优于其他两种算法。

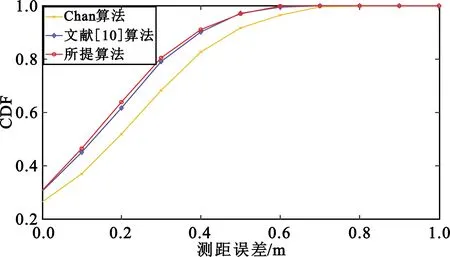
图3 近场目标各算法的CDF对比图

4.2 远场目标仿真

相比于近场目标的仿真结果，各算法对远场目标的定位精度较差，相同噪声下，所表现的RMSE较高。这是由于声源目标越远离传感器受到水下环境的影响越大，定位性能也相对下降。由图4可知，当测距误差大于1 m时，Chan算法和文献[10]算法已经严重偏离CRLB，本文所提算法虽有些偏离，但依然好于其他两种算法；当测距误差为10 m时，所提算法的定位误差相比于Chan算法和文献[10]算法分别减少了108.16 m和17.64 m，算法整体的定位精度分别提高了84.1%和10.7%，说明对于远场目标，噪声较大时，本文算法相比于其他两种算法依然有着良好的抗噪声性能。

图4 远场目标各算法的RMSE对比图

图5和图6分别比较了对远场目标的定位偏差和各算法的CDF曲线，从图中可以看出本文所提算法定位偏差最小且CDF曲线上升最快，进一步证明了本文所提算法的定位性能远远优于其他两种算法。

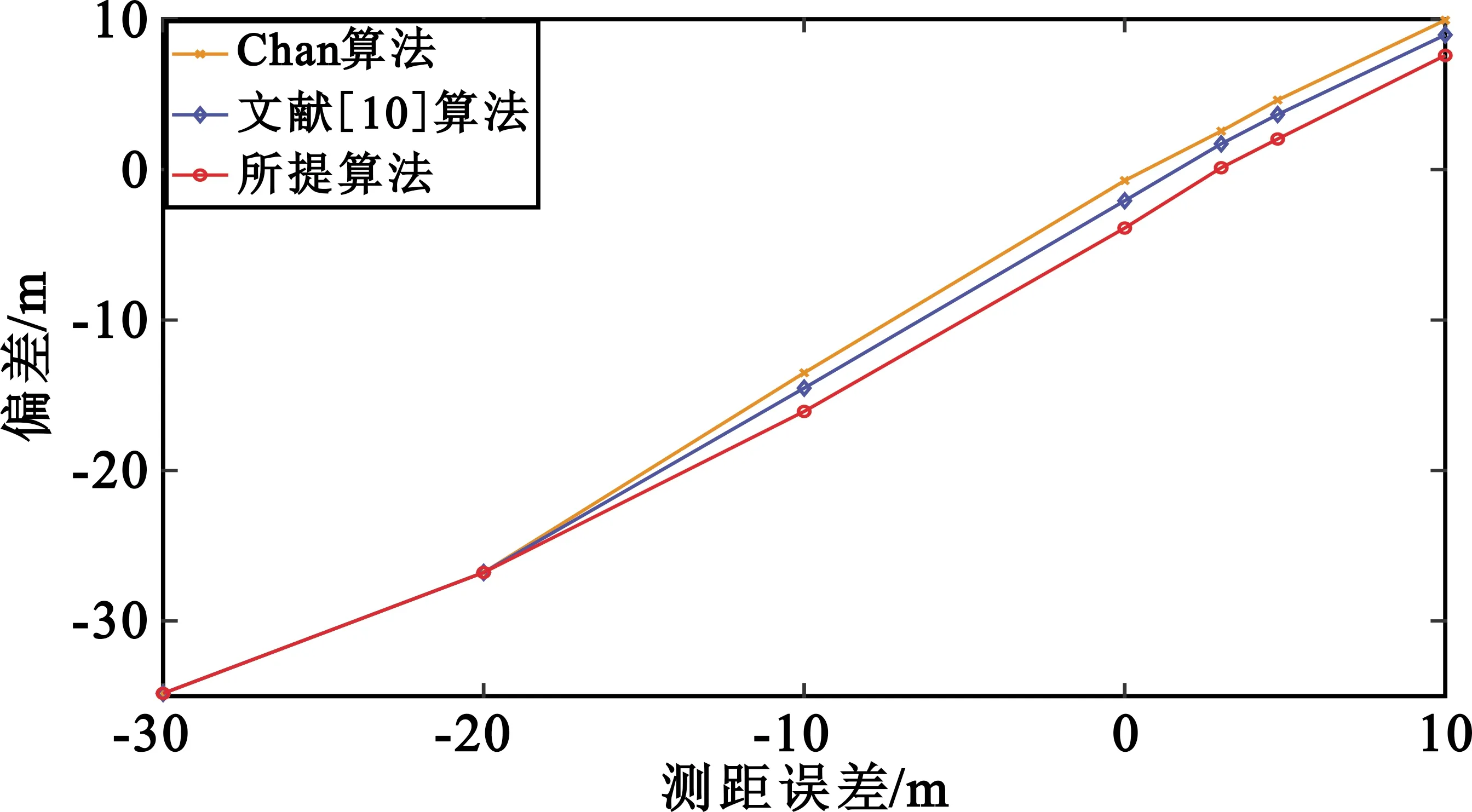
图5 远场目标各算法的偏差对比图

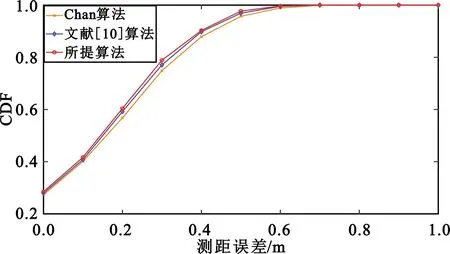
图6 远场目标各算法的CDF对比图

5 结 论

针对现有的TSWLS水下目标定位算法在计算过程中忽略二阶误差项，导致定位精度下降问题，本文提出了一种改进的TSWLS算法，有效避免了二阶误差项的丢失。理论分析和仿真实验结果表明，不管是近场目标还是远场目标，本文所提算法始终保持良好的定位性能和抗噪声性能。