低空超高速运动平台测高算法*
张文鑫
(北京信息科技大学 自动化学院,北京 100192)
0 引 言
随着现代高科技武器装备的发展,已经形成了以低空/超低空突防、隐身技术、电子干扰和反辐射导弹为主体的对雷达探测系统的四大威胁。其中,低空/超低空突防属于战术范畴,与其他三者相比,在实战中灵活性更强,威胁更大,对抗难度更高。由于雷达探测技术的不断提高,高空飞行极其容易被侦测,因此越来越多的国家将低空和超低空飞行作为突防的重点手段。一般将飞行高度为1 000 m以内称为低空飞行,10~300 m称为超低空飞行。由于飞行速度极快,因此低空和超低空飞行需要准确的实时高度信息[1-2]。
雷达高度表是一种主动的遥感设备,最初用于测量地面上空的飞行器高度,后来逐渐扩展到其他方面如控制投弹、低空导航和地形回避等应用。由于调频连续波(Frequency Modulated Continuous Wave,FMCW)雷达具有发射功率低、接收机灵敏度较高、距离分辨力高且没有盲区、结构简单等优点,军用雷达高度表大多采用FMCW体制的雷达,但传统的FMCW雷达会受到多普勒徙动和距离徙动[3-4]的影响。
近年来,随着低空高速打击备受各国重视,高速运动目标的测距测速问题显得尤为重要。为得到更精确的目标定位效果,国内外学者提出了一些检测算法,如Keystone变换[5]、RFT变换[6]、Hough变换[7]、FRFT的时频分析法[8-9]、长相干积分法[10-12]、惯导补偿法[13]、缩放逆傅里叶变换[14]等。
经过几十年的研究,超高速目标雷达检测方法取得了较大进展,但是仍然存在一些问题[15]:一是已有算法只考虑一些常见的简单运动模型,如匀速直线运动模型和匀加速直线运动模型,但实际目标运动非常复杂,需要建立更加普适的回波模型;二是算法工程化实现,高速运动目标检测要求较少的计算量和较高的实时性;三是多目标超高速运动检测问题,现阶段的算法更多是针对单一目标的研究。针对低空超高速运动平台的高度测量,同样存在上述问题。为此,本文提出一种脉冲频移调频(Pulse Frequency Modulated Shift Keying,PFMSK)调制波形来适用于多种运动模型,结合自适应移位能量归一化变换(Shift Normalized Energy Transform,SNET) 算法可以大大减小计算量,提高算法的实时性。
1 信号模型
1.1 FMCW信号模型
FMCW体制雷达发射的上扫频信号可以表示为
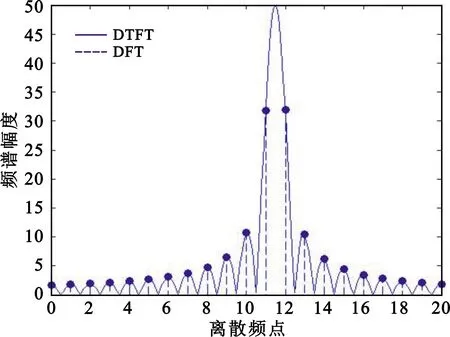
vT(t)=exp[j(2πf0t+πBt2/T+φ0)],0≤t (1) 式中:f0为发射信号扫频起始频率,B为发射信号扫频带宽,T为扫频周期,φ0为初始相位。其调频斜率为K=B/T。距离为r处的目标的回波信号可以表示为 vR(t)=exp{j[2πf0(t-td(t))+πB(t-td(t))2/T+φ0] }, (2) v1(t)=exp{j[2πf0td(t)+2πKtd(t)t-πKtd(t)2] } 。 (3) 忽略延时高次项πBtd(t)2/T,可得 v1(t)=exp{j[2π(2f0R1/c+2KR1/c·t+2f0V(t)/c+2KV(t)t/c)] } 。 (4) 式(4)中包含时间的零次项、一次项和高次项,其中零次项为相位固定相位,不影响频率;一次项中包含距离和速度引起的中频信号频率,成为距离速度耦合现象;当速度较小时,高次项可以忽略,但是当速度较大时,忽略高次项会引入误差。对中频信号的相位求导得到上扫频的中频信号时频分布为 (5) v2(t)=exp{j[2π(2f1R2/c-2KR2/c·t+2f1V(t)/c-2KV(t)t/c)] } 。 (6) 式中:f1=f0+B,t∈[T,2T]。下扫频中频信号的时频分布为 (7) 基于三角波FMCW体制的雷达测距测速算法,假设目标做匀速直线运动,且速度比较小,v(t)=v,则V(t)=v·t,R2=R1,并忽略发射信号起始频率差和中频信号中时间的高次项,距离和速度的估计值分别为 (8) (9) 通过式(5)和式(7)可知,当满足上述假设时,式(8)和式(9)计算得到的距离和速度几乎与理论的距离和速度相等,但是当运动速度很大且不是匀速直线运动时,发射信号起始频率差和中频信号中时间的高次项不能忽略。 F1(t)+F2(t)=2KR1/c+2KR2/c+ d[2f0V(t)/c+2KV(t)t/c]/dt}|t∈[0,T]- d[2f1V(t)/c-2KV(t)t/c]/dt|t∈[T,2T], (10) F1(t)-F2(t)=2KR1/c-2KR2/c+ d[2f0V(t)/c+2KV(t)t/c]/dt}|t∈[0,T]+ d[2f1V(t)/c-2KV(t)t/c]/dt|t∈[T,2T]。 (11) 当速度较大时,得到的距离估计值误差较大,当带宽载频比较大时速度估计误差较大。实际情况下目标的运动模型可能非常复杂,不能假设为简单的匀速或者匀加速来建立模型。实际计算时,利用傅里叶变换将时域信号变换到频域,没有时间分辨率,因此很难得到准确的上扫频和下扫频的时频函数,得到的只是在扫描周期内信号各频率成分的加权。 本节基于1.1节分析的结果,提出一种分叉型的发射波形,如图1所示。其中T1段为上扫频,T2段为固定频点,T3段为下扫频,三段信号相互交叉周期更迭,系统实现方案可以利用射频开关进行切换。 图1 PFMSK体制发射波形 从时频图上看,波形类似于FSK波形,且被分为了多个脉冲,因此本文将这种分叉型的发射波形称为脉冲频移调频体制。其中,T1上扫频发射信号模型为 vT1(t)=exp[j(2πf0t+πBt2/T+φ1)],0≤t (12) 中频信号为 v1(t)=exp{j[2π(2f0R1/c+2KR1/c·t+2f0V(t)/c+2KV(t)t/c)] } , (13) vT2(t)=exp[j(2πf0t+φ2)],0≤t (14) 中频信号为 v2(t)=exp{j[2π(2f0R1/c+2f0V(t)/c)] } 。 (15) T3下扫频发射信号模型为 vT3(t)=exp[j(2πf0t-πBt2/T+φ3)],0≤t (16) 中频信号为 v3(t)=exp{j[2π(2f0R1/c-2KR1/c·t+2f0V(t)/c-2KV(t)t/c)] } 。 (17) 由于三段信号的时间区间都属于[0,T],利用T2时间段的中频信号与T1和T3时间段的中频信号进行混频: (18) 利用倒谱原理可以提取T2时间段中频信号除去初始相位的相位时变函数: φ(t)=ln(v2(t))=4πf0V(t)/c 。 (19) 对得到的相位时变函数进行一定变换: φ(t)=φ(t)·Kt/f0=4πKV(t)t/c 。 (20) 构建误差补偿信号: vv=exp{j[φ(t)] }=exp{j[4πKV(t)t/c] } 。 (21) 利用构建的误差补偿信号和式(18)进行混频得到校正信号 (22) 因此可以通过已有的频谱分析算法,如CZT、ZFFT等算法对上式的频率进行估计,计算得到中频信号频率再对距离进行估计,但是由于飞行速度极快,因此对计算的实时性要求较高。本文提出一种自适应的频率估计算法。 根据上一节的分析可知,对目标精确的测距就是对信号s1和s2的精确频率估计,现有的谱估计算法所需计算量较大,而高速运动目标测距要求实时性很高。为了进一步减少运算量,并满足更高的精度要求,本节提出基于帕塞瓦尔(Parseval)能量守恒定理自适应的频率估计方法,并称之为移位能量归一化变换。 已知序列x(n)的长度为N,其离散傅里叶变换(Discrete Fourier Transform,DFT)为 (23) 则有帕塞瓦尔能量守恒定理: (24) DFT具有移位性质: (25) 由式(23)~(25)可以推导出 (26) 式(26)为一恒等式,且等于常数C,C为序列x(n)的能量和。 假设采样率为Fs且满足采样定理,采样点数为N,则其频率分辨力为Fs/N。对式(22)离散化: v(n)=exp{j[2π(2BR1n/c/N)] },0≤n (27) 对v(n)做单边离散傅里叶变换: (28) 其DFT谱和离散时间傅里叶变换(Discrete Time Fourier Transform,DTFT)谱如图2所示。由图2可以看出,DFT是对DTFT的离散采样,当中频信号频率不为频率分辨率Fs/N的整数倍时,中频信号的DFT-DTFT图如图2(a)所示;利用式(25)将中频信号频谱向右进行移位,当移位后信号的DFT频谱峰值点进行交替,对应的频率F1为Fs/N的整数倍加Fs/2/N,可以表示为F1=(M+1/2)·Fs/N,如图2(b)所示;继续将中频信号的频谱向右进行移位,当DFT的峰值点所对应的频率F2为Fs/N的整数倍,可以表示为F2=M·Fs/N,M为整数,其峰值点的幅值达到最大,如图2(c)所示。 (a)非特殊频率 (b)频率分辨率(N+0.5)倍 (c)频率分辨率N倍图2 中频信号的移位DFT和DTFT (29) 图2(b)对应的归一化能量最大,因为图2(b)处于峰值交替位置,其|X(km)|最小;而图2(c)对应的峰值幅度最大,因此归一化能量最小。移位后单周期内归一化能量如图3所示。 图3 中频信号的移位归一化能量图 中频信号的移位归一化能量在相邻频率点之间呈现周期性的变化,且在频率点左右的半周期内归一化能量是凹函数,因此可以通过归一化能量找出特征点所对应的频率。 方法1:找出归一化后能量最大值A点,A点对应于图2(b),求出移位后频率F1,则F1=(M+1/2)·Fs/N,N为采样点数,M为移位前峰值对应的Fs/N整数倍频率位置,在进行反向推演即可求出移位前的中频信号频率。假设频谱移动的频率为delta,则有F1=f+delta,其中f为中频信号频率,则f=(M-1/2)·Fs/N-delta。 方法2: 也可以找出移位后归一化能量最小值B点,B点对应于图3(c),求出移位后频率F2,则F2=M·Fs/N,N为采样点数,M为移位后峰值对应的Fs/N整数倍频率位置,再进行反向推演即可求出移位前的中频信号频率。假设频谱移动的频率为delta,则有F2=f+delta,其中f为中频信号频率,则f=M·Fs/N-delta。 从归一化后能量分布可以看出,B点附近能量值渐变,A点是一个奇异点,因此当有噪声影响时,B点能量由于极值点相差不大,更容易受噪声影响而导致极值点提取错误,因此利用A点正确计算频率的可靠性更高。 为了减少计算量,最好从A点附近开始,先通过已有算法,如能量重心法,对频率进行一次估计,然后利用DFT的移位性质将频谱移动到A点附近,再利用上述SNET算法对频率进行进一步估计。由于能量重心法需要快速傅里叶变换(Fast Fourier Transform,FFT)计算,因此需要的复数乘法较多,而在高速飞行过程中,每增加一定的运算量都有可能得不到准确的实时距离值。由式(19)可知 (30) 利用T2时间段内回波的相位差计算一个扫频周期内飞行器距离的变化值ΔR(t),假设准确计算出第n个周期位置处的距离值Rn,则可以估计第n+1周期起始位置的距离值 Rn+1=Rn+ΔR(t) 。 (31) 因此可以利用上式估计下一个周期起始位置的距离值,利用DFT的移位性质可将中频信号频谱移动到图3中的A点附近,根据系统要求的测距精度设置合适的门限值。 (32) 本算法执行过程中所需运算量大小主要体现在傅里叶变换复数运算上。由于复数乘法比复数加法需要4倍的运算时间,因此,本文分析运算量只考虑复数乘法。利用DFT移位性质可知, (33) 根据上述对超高速运动平台发射波形的设计和算法分析,本节利用Matlab软件对其进行系统建模。仿真中采用C频段雷达系统,起始频率为4 GHz,带宽为100 MHz,扫频周期为1 ms,采样率为2 MHz;飞行器飞行起始高度为193 m,飞行速度为3Ma(1Ma=340 m/s),飞行方向往上飞,且加速度为340 m/s2;中频信号信噪比为5 dB。同时利用传统FMCW体制和本文提出的PFMSK体制雷达,对比两种体制下测距误差。假设系统要求的测距精度为系统分辨率的1/25,传统FMCW体制使用CZT算法测高,细化倍数为25倍,仿真测距误差如图4所示。通过门限计算方法得到PFMSK体制所需要的门限值为1+24/26,仿真测距误差如图5所示。 图4 FMCW测高误差 图5 PFMSK测高误差 根据上述参数设置,雷达系统的分辨率为1.5 m,系统要求的测距精度为6 cm。利用FMCW体制雷达测距误差为0.5~0.7,且呈一定上升趋势。造成这种误差的原因主要是FMCW体制雷达测距算法中认为目标是做匀速运动且在扫频周期内目标距离几乎不变,但是实际在超高速运动平台上目标速度很快,导致在扫频周期内目标距离在逐渐变化,且此变化不能被忽略,同时运动目标存在一定加速度,在每一次测距周期内速度都不恒定,导致了误差出现一定斜率且往上偏移,这就是多普勒徙动和距离徙动。 计算仿真所产生的1 000组数据,利用Matlab记录算法运行时间,本文所提算法耗时1.1 s,CZT算法耗时1.7 s,因此本文所提算法效率比传统频谱细化算法更高。 本文所提出的PFMSK算法同时考虑了目标的速度加速度对测距结果的影响,通过回波本身的特性进行了补偿和抵消,采用实时高度跟踪法只计算对应距离频谱值,大大减小了计算量和计算时间,同时具有较高的测距精度,可以满足高速运动平台的实时测高应用。 本文主要研究低空超高速运动平台的测高算法,分析了已有FMCW体制雷达在高速运动平台测高的不足,提出了一种新的调制发射波形,本文将其命名为脉冲频移调频体制。针对复杂地面模型,利用中频混频技术补偿高速多普勒频移具有一定普适性,提出一种SNET的自适应测高算法。该算法不但具有较高的实时性,同时测高精度可以满足系统要求。超高速条件下FMCW和PFMSK两种体制下的测高算法的仿真对比表明,由于受加速度和速度的影响,FMCW误差较大,而PFMSK误差可以很好地控制在系统要求的范围内,验证了本文理论分析的正确性。
td≤t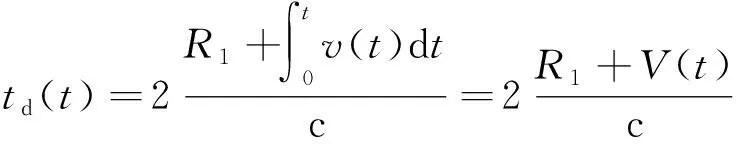
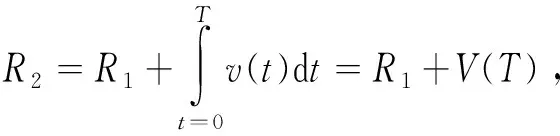
1.2 PFMSK波形设计

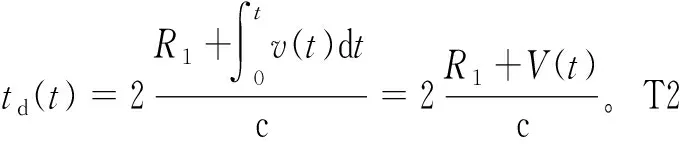
2 自适应测距算法实现
2.1 帕塞瓦尔定理
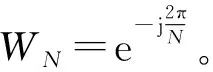
2.2 移位归一化变换



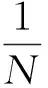

2.3 自适应高度跟踪


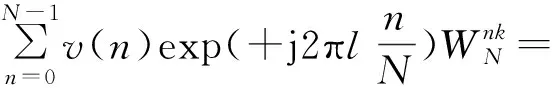

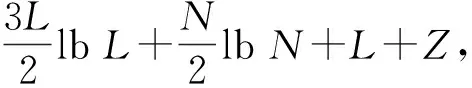
3 算法仿真


4 结 论

