双推杆肢腿机构运动特性数值模拟与试验研究

赵富强，吴红庆，杜鹏阳，牛志刚

（1.太原科技大学重型机械教育部工程研究中心，山西 太原 030024；2.太原理工大学极地工程与装备研究院，山西 太原 030024）

1 引言

肢腿机构是移动机器人运动和承载的关键部件，因其结构和运动方式不同，具有较强的环境适应性，现有的肢腿机构常采用关节电机驱动，但其承受的外力矩较小，无法适用于重载场合[1]。双推杆肢腿机构作为南极科考机器人[2]构型中连接履带足和中心平台的承载构件组，既对极端地形具有良好的适应性又兼备良好的承载能力。因此，有必要对双推杆肢腿机构开展运动学分析研究。

目前针对移动机器人的运动学已开展了大量研究，文献[3]对一种三自由度六足腿式机器人并联驱动机械腿机构进行了运动学静力学性能评价及几何参数优选。文献[4]提出了一种基于3-UPS机构的六自由度并联机械腿，并进行了运动学分析与运动灵活性评价。文献[5]提出了一种液压驱动六足跳跃机器人模型，对该机器人侧面双腿和正面双腿竖直跳跃进行了运动学分析。文献[6]提出了一种通过轮式与足式相互切换实现多种操作模式的新型轮腿复合机器人，给出了机器人支链末端的可达工作空间与移动过程中的运动轨迹。文献[7]针对同时具有被动关节和柔性杆的欠驱动平面机械臂，分析了系统的动力学耦合特性。文献[8]研制开发了一种多运动模式的小型轮履腿复合式移动机器人，对其运动特性、越障性能、自动复位功能进行了详细的分析。文献[9]提出一种新型轮腿式移动机器人，将攀爬楼梯作为越障任务和设计目标，进行了力学分析和参数设计，研究了轮腿结构参数对机器人抗冲击能力和续航能力的影响规律。

文献[10]分析了链驱动喷涂机器人的优缺点和末端轨迹精度的影响状况，并结合机器人本体的运动学参数，建立了基于随机变量的喷涂机器人运动误差模型。文献[11]提出一种基于运动学分析的工业机器人轨迹精度补偿方法，并建立了曲线运动轨迹偏差与运动学模型参数误差映射的机器人运动轨迹误差数学模型。文献[12]以三自由度Delta并联机械手为研究对象，对高速搬运作业下的操作空间和关节空间的轨迹规划策略进行了研究。文献[13]基于机械臂关节空间和操作空间的速度映射关系，建立了机械臂末端运动学方程。上述研究主要集中在关节电机驱动下对开环机构运动学特性的研究，对推杆驱动研究较少，因此研究双推杆肢腿机构可提高其承载能力，拓展其应用领域。

以南极科考机器人双推杆肢腿机构为研究对象，对其在一级推杆独立驱动、二级推杆独立驱动、双推杆同步驱动三种典型运动工况下，进行运动学分析和试验研究，揭示各肢腿角度变化，下肢腿末端运动轨迹、速度和加速度运动特性变化规律。

2 双推杆肢腿机构

2.1 构型分析

双推杆肢腿机构是南极科考机器人构型中连接履带足和中心平台的承载构件组。南极科考机器人主要由中心平台和均布在中心平台端角位置上的6条肢腿和履带足组成，南极科考机器人通过各个双推杆肢腿机构这一运动单位协同运动实现抬腿、越壑和避障等功能，如图1所示。

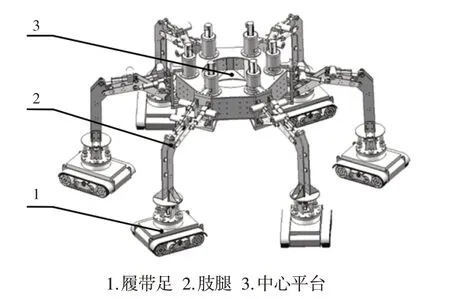
图1 南极科考机器人Fig.1 Antarctic Research Robot

双推杆肢腿机构主要由支架、上肢腿、下肢腿、一级推杆和二级推杆组成，如图2所示。其中，上肢腿上端与支架相连，下端与下肢腿上端相连，一级推杆安装在支架与上肢腿之间，二级推杆安装在上肢腿与下肢腿之间。双推杆分别驱动上肢腿和下肢腿，使肢腿实现往复转动，整个过程中双推杆肢腿机构始终保持在同一平面内运动。

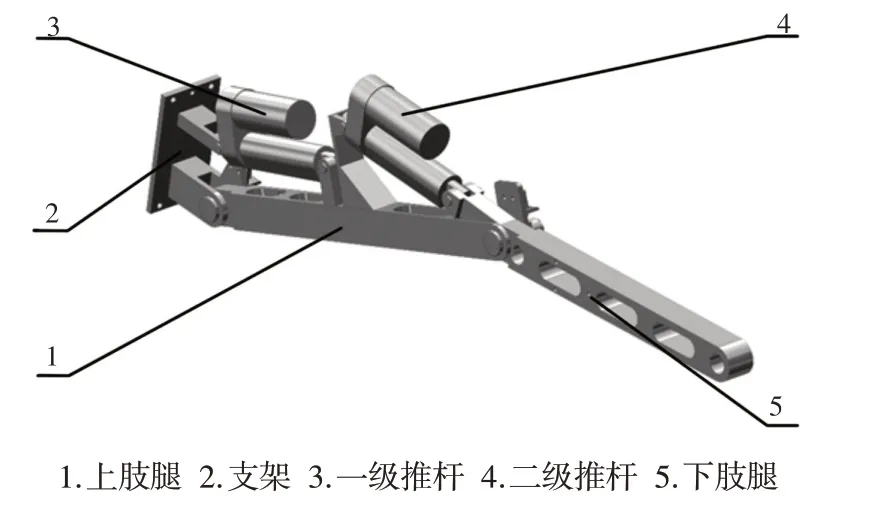
图2 双推杆肢腿机构模型图Fig.2 Double Push Rod Leg Mechanism Model

2.2 运动分析

双推杆肢腿机构以推杆收缩状态为初始位置，主要分析三种典型运动工况下的运动，如图3所示。

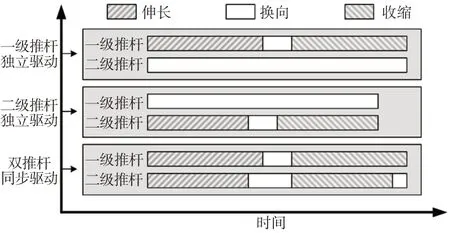
图3 运动工况图Fig.3 Motion Condition

（1）一级推杆独立驱动：一级推杆从收缩状态开始伸长，到达最顶端处停止，经过换向后开始收缩，最后收缩到初始位置处停止，其中二级推杆在整个过程中保持收缩状态不动，上肢腿先顺时针转动后逆时针转动到初始位置，下肢腿与上肢腿之间的夹角保持不变。

（2）二级推杆独立驱动：二级推杆从收缩状态开始伸长，到达最顶端处停止，经过换向后开始收缩，最后收缩到初始位置处停止，其中一级推杆在整个过程中保持收缩状态不动，上肢腿与支架之间的夹角保持不变，下肢腿先顺时针转动后逆时针转动到初始位置。

（3）双推杆同步驱动：双推杆同时从收缩状态开始伸长，二级推杆先到达最顶端处停止，随后一级推杆到达最顶端处停止，经过换向后双推杆同时开始收缩，二级推杆先收缩到初始位置处停止，最后一级推杆收缩到初始位置处停止，整个过程中上肢腿和下肢腿都是先顺时针转动后逆时针转动到初始位置。

3 双推杆肢腿机构运动学数值分析

3.1 运动学方程

为揭示各肢腿角度，下肢腿末端运动轨迹、速度和加速度的变化规律，对双推杆肢腿机构进行运动学分析，推导下肢腿末端轨迹、速度和加速度方程。以O为原点建立全局坐标系OXY，如图4所示。图中：l1和l2—上、下肢腿的长度；θ1—上肢腿相对于X轴方向的角度；θ2—下肢腿相对于X轴方向的角度，其中肢腿角度在X轴上方为正，在X轴下方为负；l3、l4—双推杆长度；lA—A、I之间距离；lK—A、J之间距离；lE—E、I之间距离；lF—F、J之间距离；lG—G、B之间距离；β—下肢腿∠GBC的夹角；hy—D、A之间距离。

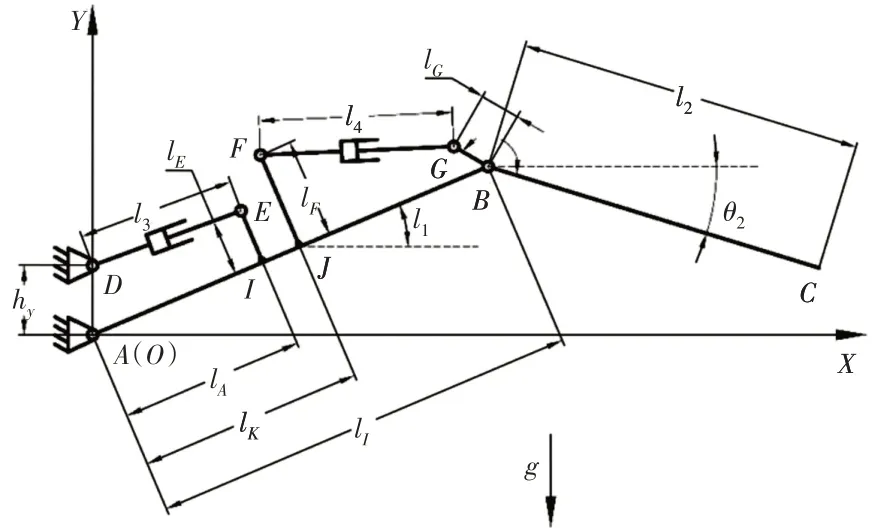
图4 双推杆肢腿机构尺寸参数Fig.4 Dimension Parameters of Double Push Rod Leg Mechanism

根据图4得到上、下肢腿质心和下肢腿末端在X、Y轴方向的位置坐标分别为：

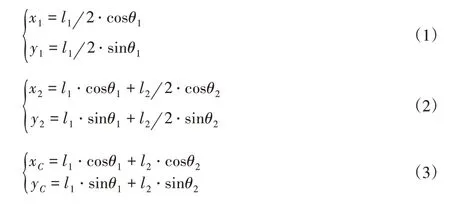
对式（1）～式（3）求导得到上、下肢腿质心和下肢腿末端在X、Y轴方向的速度分别为：

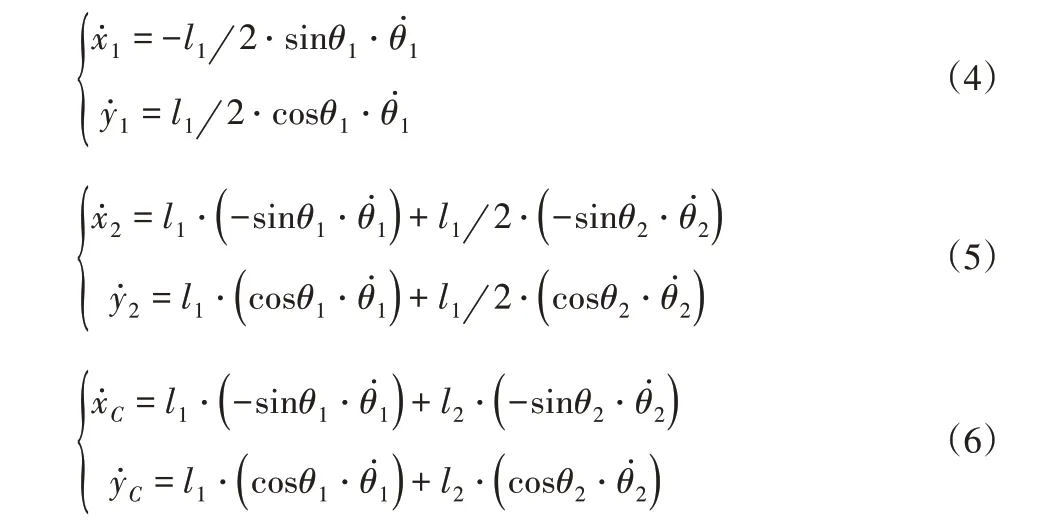
对式（1）～式（3）二次求导得到上、下肢腿质心和下肢腿末端在X、Y轴方向的加速度分别为：

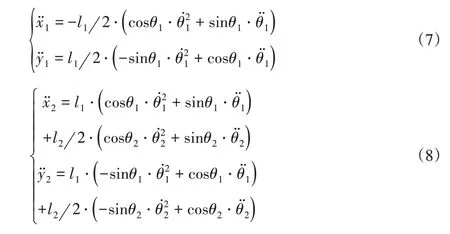
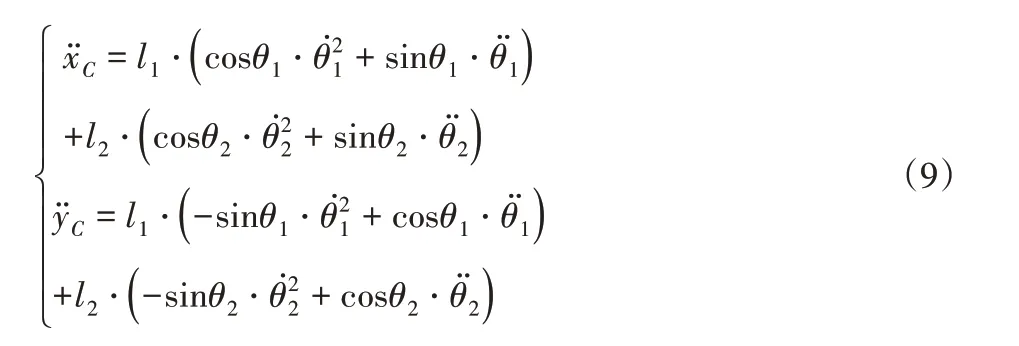
3.2 数值模拟

为得到双推杆肢腿机构在一级推杆独立驱动、二级推杆独立驱动、双推杆同步驱动三种典型运动工况时上肢腿和下肢腿相对于X轴方向的角度，下肢腿末端运动轨迹、速度和加速度等动态特性曲线，对双推杆肢腿机构进行运动学数值模拟，如图5所示。参数，如表1所示。考虑测试过程中出现偏差和延迟，将试验测得的三种典型运动工况下推杆驱动时间分别设置到仿真中得到其仿真结果，如表2所示。在初始时刻，双推杆都处于初始位置。

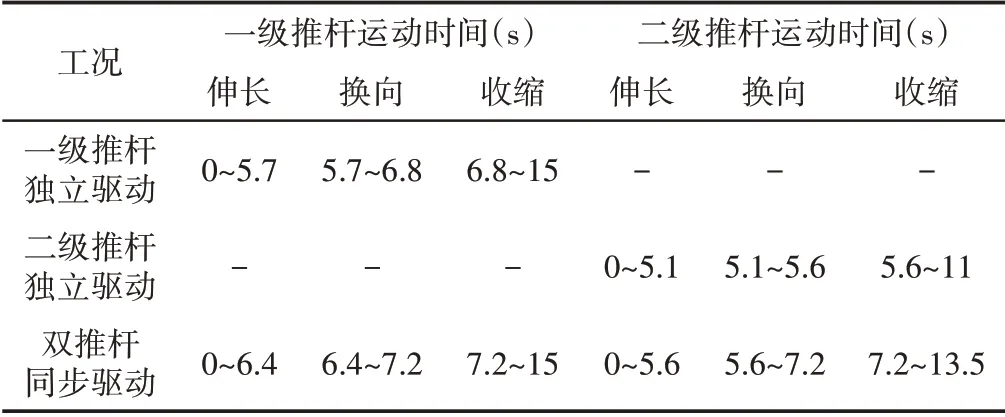
表2 运动工况参数Tab.2 Parameters of Motion Condition

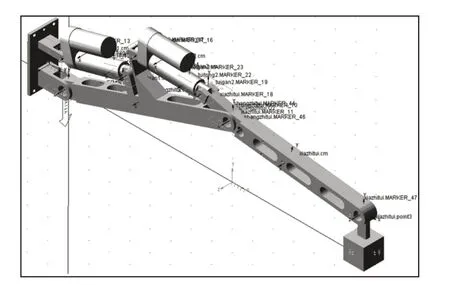
图5 双推杆肢腿机构仿真模型Fig.5 Simulation Model of Double Push Rod Leg Mechanism

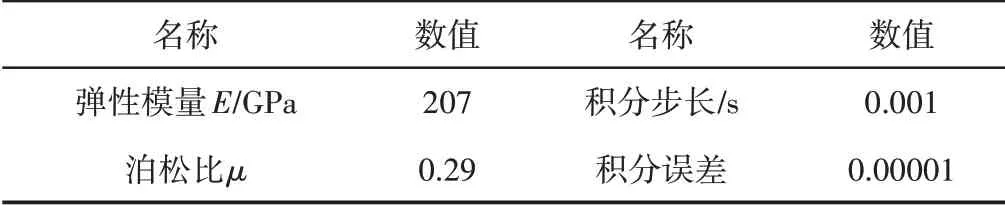
表1 双推杆肢腿机构仿真参数Tab.1 Simulation Parameters of Double Push Rod Leg Mechanism

双推杆驱动主要由伸长、换向和收缩三个阶段组成，具体如下。

（1）伸长阶段：推杆从收缩状态开始出发，伸长50mm后到达推杆最顶端处停止；

（2）换向阶段：推杆在到达最顶端后开始换向为下一阶段做准备；

（3）收缩阶段：推杆从最顶端处开始收缩，收缩50mm后回到初始位置。

4 试验研究

为验证双推杆肢腿机构的运动学方程，对上述三种典型运动工况开展上肢腿和下肢腿相对于X轴方向的角度，下肢腿末端运动轨迹、速度和加速度试验测试，如图6所示。

图6 双推杆肢腿机构试验台Fig.6 Double Push Rod Leg Mechanism Test-Bed

试验测试平台采用低通滤波算法对试验数据进行噪声处理，上肢腿和下肢腿分别由XTL100电动推杆驱动，其角度变化由HWT905-232角度传感器实时测量，数据由USB3104A数据采集仪采集，如表3所示。通过式（3）、式（6）和式（9）得到双推杆肢腿机构末端运动轨迹、速度和加速度曲线。本试验测试平台在25dB、20℃干摩擦下进行，其中销轴与轴套之间的动摩擦系数为0.25，静摩擦系数为0.3。销轴和轴套粗糙度为6.3，可通过加工满足其精度要求。

表3 设备参数Tab.3 The Equipment Parameters

5 双推杆肢腿机构动态响应分析

5.1 评价指标

对双推杆肢腿机构进行运动学仿真与测试，得到上肢腿和下肢腿相对于X轴方向的角度，下肢腿末端运动轨迹、速度和加速度等动态特性理论与试验曲线，并对仿真与试验结果进行一致性对比分析。受到机械结构本体试验条件限制，试验与仿真结果误差不可避免，采用相关系数(R)指标和平均相对误差(AARE)指标评价理论与试验中运动特征参数的一致性程度。其中，R用以反映变量之间相关关系密切程度的统计指标，R越高则试验值与仿真值之间的拟合程度越好；AARE指的是所有测量点测量所造成的绝对误差与被测量真值之比的平均值，AARE越小则测量数值越接近测量真值，其表达如下：

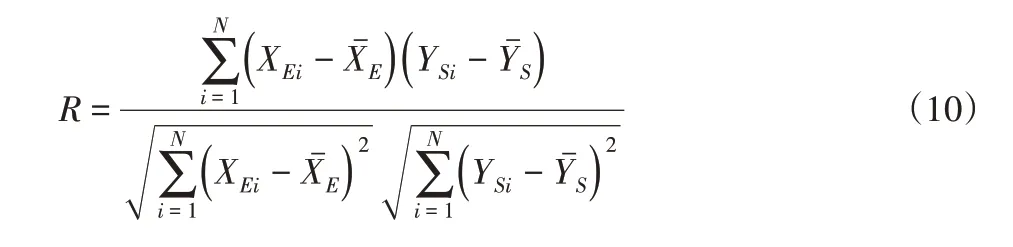
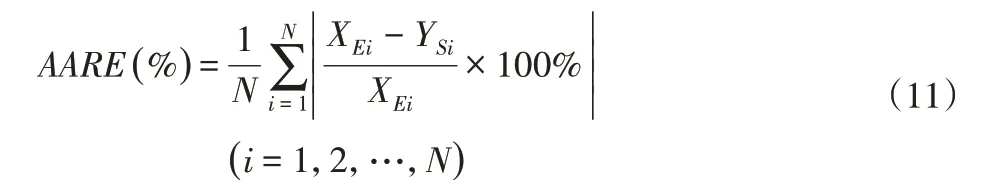
式中：XEi—试验得到的实际测量值；XSi—仿真得到的数值模拟值；XE和XS—XEi和XSi的平均值；N—试验数据的个数。

5.2 一级推杆独立驱动运动特性

双推杆肢腿机构在一级推杆独立驱动时，上肢腿和下肢腿相对于X轴方向的角度呈先减小后增大的变化规律，如图7、图8所示。在（0～5.7）s伸长阶段和（6.8～15）s收缩阶段，各肢腿角度呈线性减小和线性增大趋势，此时下肢腿末端速度在一级推杆独立驱动下做匀速运动。在（5.7～6.8）s换向阶段，各肢腿角度保持不变，此时双推杆肢腿机构静止。由表4可知，θ1的相关系数和平均相对误差分别为0.9988和16.69%，θ2的相关系数和平均相对误差分别为0.9954和5.68%。

图7 上肢腿θ1角度Fig.7 Upper Limb Leg θ1 Angle

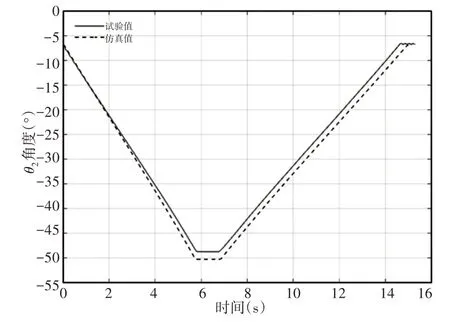
图8 下肢腿θ2角度Fig.8 Lower Limb Leg θ2 Angle

双推杆肢腿机构在一级推杆独立驱动时，下肢腿末端运动轨迹是平滑连续的二次函数曲线，如图9所示。下肢腿末端运动轨迹从（720，100）开始出发，随一级推杆伸长逐渐移动到（590，-425），经过换向后在一级推杆收缩下回到初始位置。由于机械结构限制的影响推杆未能到达最顶端，导致下肢腿末端不能在（590，-425）与（600，-410）之间运行，因此在这区域中只存在仿真值。由表4可知，下肢腿末端运动轨迹曲线试验值与仿真值在X轴方向上的相关系数和平均相对误差分别为0.9995和0.77%，在Y轴方向上的相关系数和平均相对误差分别为0.9989和14.18%，表明双推杆肢腿机构在Y轴方向更易受到干扰。由于机构在Y轴方向受到重力作用，当推杆伸长时重力做正功，收缩时重力做负功，因此重力对双推杆肢腿机构具有较大影响。

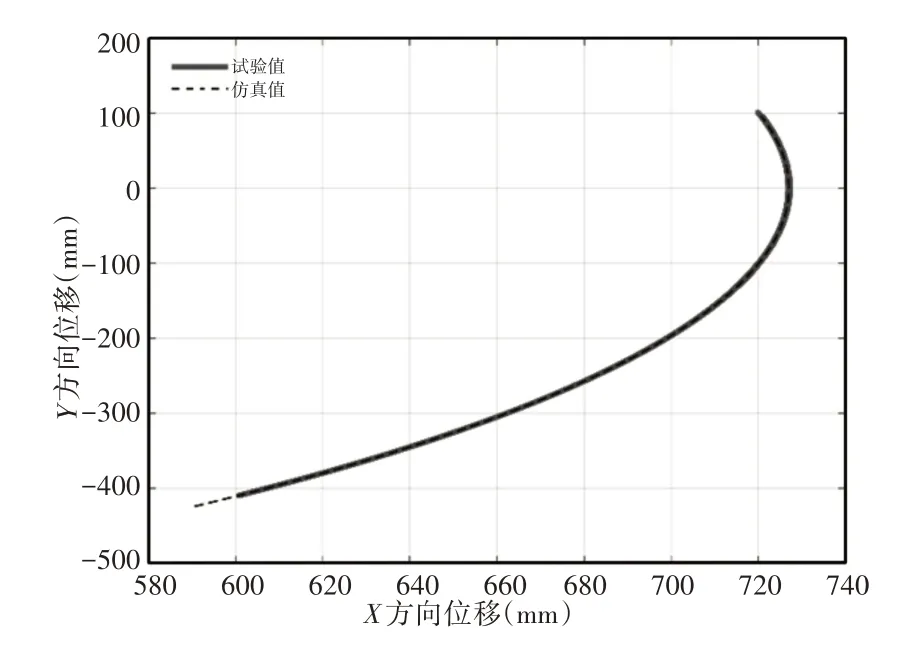
图9 下肢腿末端运动轨迹Fig.9 The Movement Track of End of Lower Limb

双推杆肢腿机构在一级推杆独立驱动时，下肢腿末端速度、加速度变化曲线，如图10、图11所示。

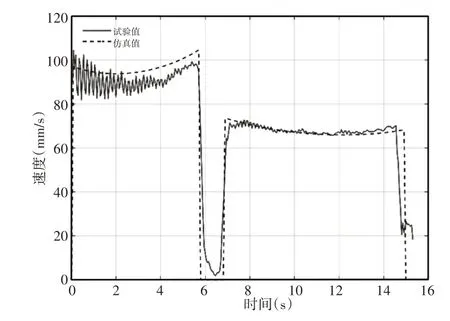
图10 下肢腿末端速度Fig.10 Velocity at the End of Lower Limb

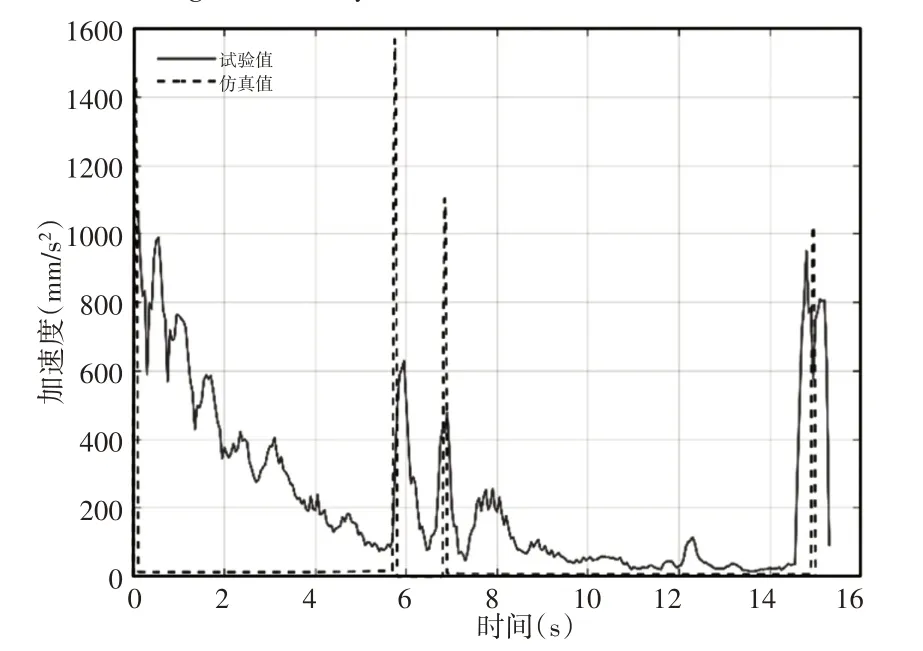
图11 下肢腿末端加速度Fig.11 Acceleration at the End of Lower Limb

下肢腿末端速度在0s、5.7s、6.8s 和14.9s 处出现阶跃响应，对应其加速度出现峰值，这是因为推杆开始伸长和结束收缩时刚性冲击造成的。在其他时间段内下肢腿末端速度趋于稳定状态而加速度趋向于0值，表明下肢腿末端速度在一级推杆驱动下做匀速运动，这与图7、图8中得到的结论一致。另外下肢腿末端速度在伸长阶段比在收缩阶段高，对应加速度数值也较高，这是推杆在运动过程中受重力影响导致的。由表4可知，下肢腿末端速度曲线试验值与仿真值的相关系数和平均相对误差分别为0.9294和11.42%，下肢腿末端加速度曲线试验值与仿真值的相关系数和平均相对误差分别为0.0912和89.88%。

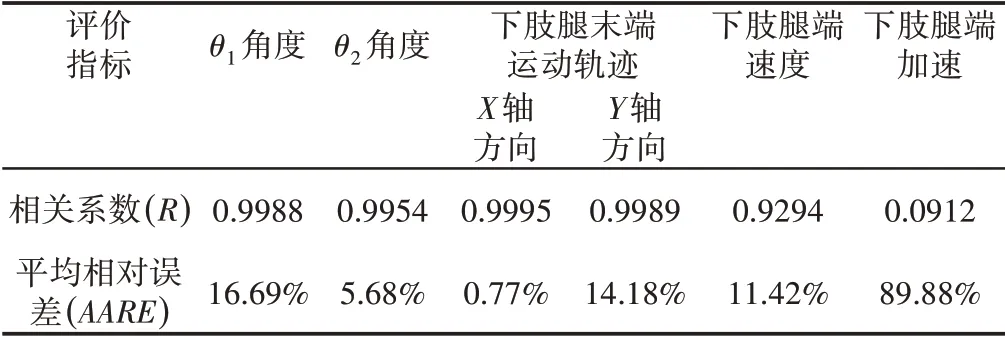
表4 一级推杆独立驱动下各参数相关系数和平均相对误差Tab.4 Correlation Coefficient and Average Absolute Relative Error of Each Parameter Under the First Push Rod Independent Drive

5.3 二级推杆独立驱动运动特性

双推杆肢腿机构在二级推杆独立驱动时，下肢腿相对于X轴方向的角度变化与一级推杆独立驱动时趋势相同，如图12所示。在（0～5.1）s伸长阶段和（5.6～11）s收缩阶段，各肢腿角度呈逐渐减小和逐渐增大趋势，此时下肢腿末端速度在二级推杆独立驱动下做变速运动。在（5.1～5.6）s换向阶段，各肢腿角度保持不变，此时双推杆肢腿机构静止。由表5可知，θ2的相关系数和平均相对误差分别为0.9599和11.09%。双推杆肢腿机构在二级推杆独立驱动时，下肢腿末端运动轨迹是平滑连续的二次函数曲线，如图13所示。

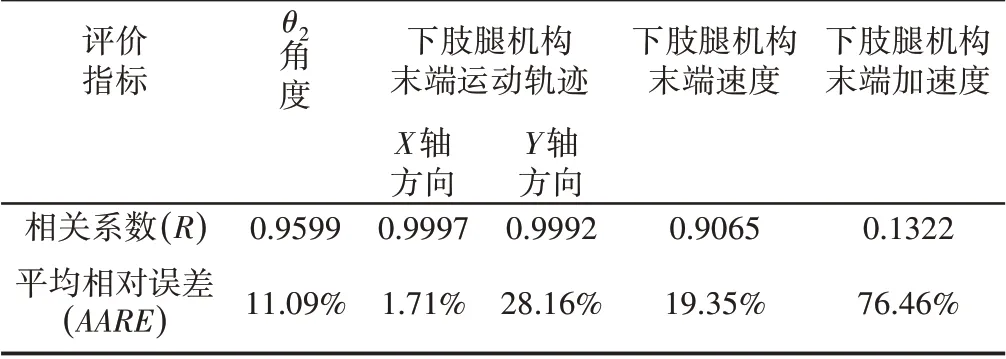
表5 二级推杆独立驱动下各参数相关系数和平均相对误差Tab.5 The Correlation Coefficient and Average Absolute Relative Error of Each Parameter Under the Secondary Push Rod Independent Drive

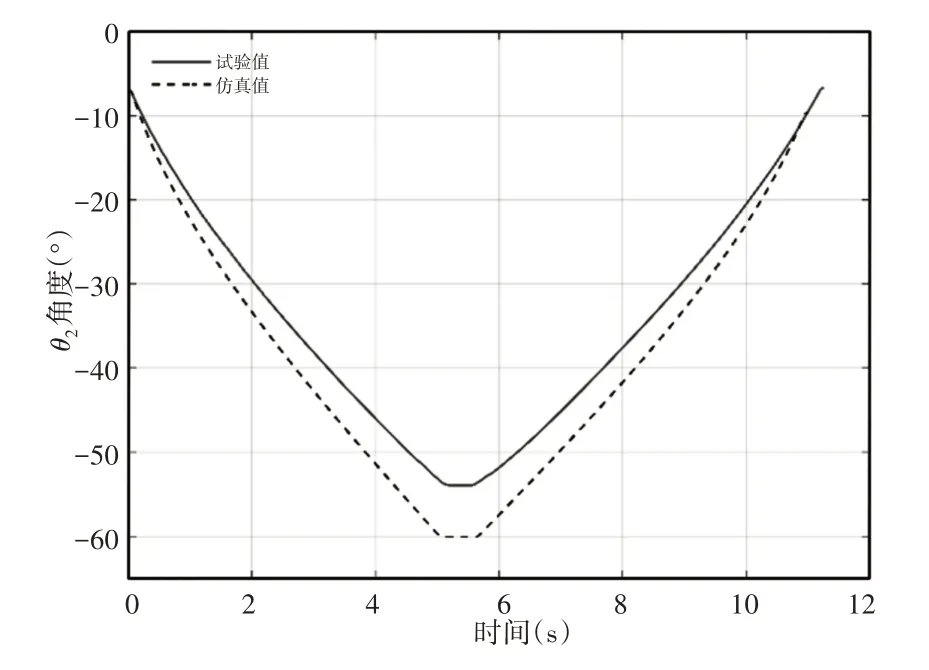
图12 下肢腿θ2角度Fig.12 Lower Limb Leg θ2Angle

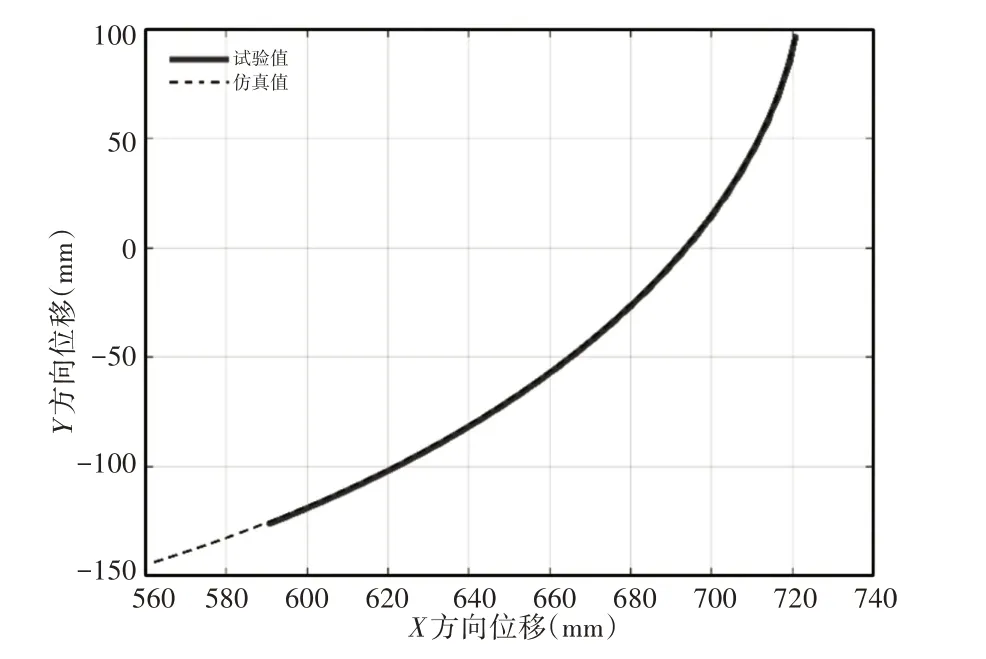
图13 下肢腿末端运动轨迹Fig.13 The Movement Track of End of Lower Limb

下肢腿末端运动轨迹从（720，100）开始出发，随二级推杆伸长逐渐移动到（560，-144），经过换向后在二级推杆收缩下回到初始位置。由表4可知，下肢腿末端运动轨迹曲线试验值与仿真值在X轴方向上的相关系数和平均相对误差分别在0.9997 和1.71%，在Y轴方向上的相关系数和平均相对误差分别在0.9992和28.16%，表明肢腿机构在Y轴方向更易受到干扰，这与一级推杆独立驱动时原因相同。

双推杆肢腿机构在二级推杆独立驱动时，下肢腿末端速度、加速度变化曲线，如图14、图15所示。

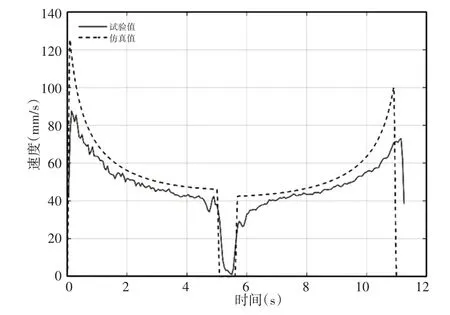
图14 下肢腿末端速度Fig.14 Velocity at the end of lower limb

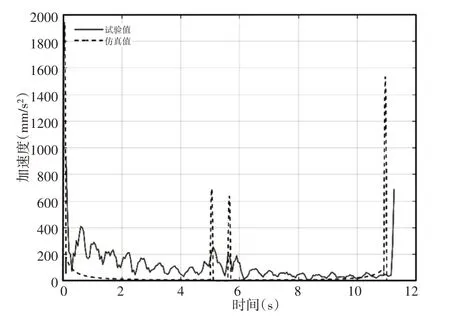
图15 下肢腿末端加速度Fig.15 Acceleration at the End of Lower Limb

发现下肢腿末端速度运行时间比一级推杆独立驱动时短，这是因为一级推杆需要承受上、下肢腿共同重力的影响，而二级推杆只需要承受下肢腿重力的影响，导致其运行时间有所不同。下肢腿末端速度曲线在0s、5.1s、5.6s和11s处出现阶跃响应，对应其加速度出现峰值，这与一级推杆独立驱动时原因相同。

由图14可知，下肢腿末端速度在二级推杆独立驱动时做变速运动，这与图12中得到的结论一致。由表5可知，下肢腿末端速度曲线试验值与仿真值的相关系数和平均相对误差分别为0.9065和19.35%，下肢腿末端加速度曲线试验值与仿真值的相关系数和平均相对误差分别为0.1322和76.46%。

5.4 双推杆同步驱动运动特性

双推杆肢腿机构在双推杆同步驱动时，上肢腿和下肢腿相对于X轴方向的角度变化与前两种运动工况趋势相同，如图16、图17 所示。一级推杆在（0～6.4）s 伸长阶段和（7.2～15）s 收缩阶段，上肢腿角度呈线性减小和线性增大趋势，此时上肢腿做匀速运动。在（6.4～7.2）s换向阶段，上肢腿角度保持不变，此时上肢腿静止。二级推杆在（0～5.6）s伸长阶段和（7.2～13.5）s收缩阶段，下肢腿角度呈逐渐减小和逐渐增大趋势，此时下肢腿做变速运动。在（5.6～7.2）s换向阶段，下肢腿角度保持不变，此时下肢腿静止。由于双推杆运行时间不同，因此下肢腿末端速度在双推杆同步驱动下做变速运动。由表6可知，θ1的相关系数和平均相对误差分别为0.9988 和6.94%，θ2的相关系数和平均相对误差分别为0.9866和8.03%。

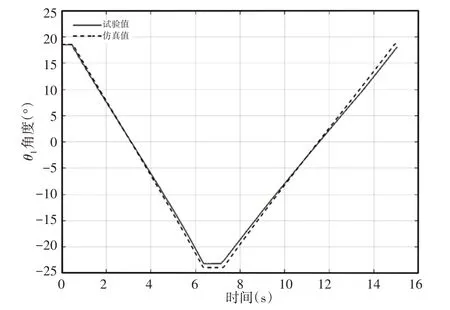
图16 上肢腿θ1角度Fig.16 Upper Limb Leg θ1 Angle

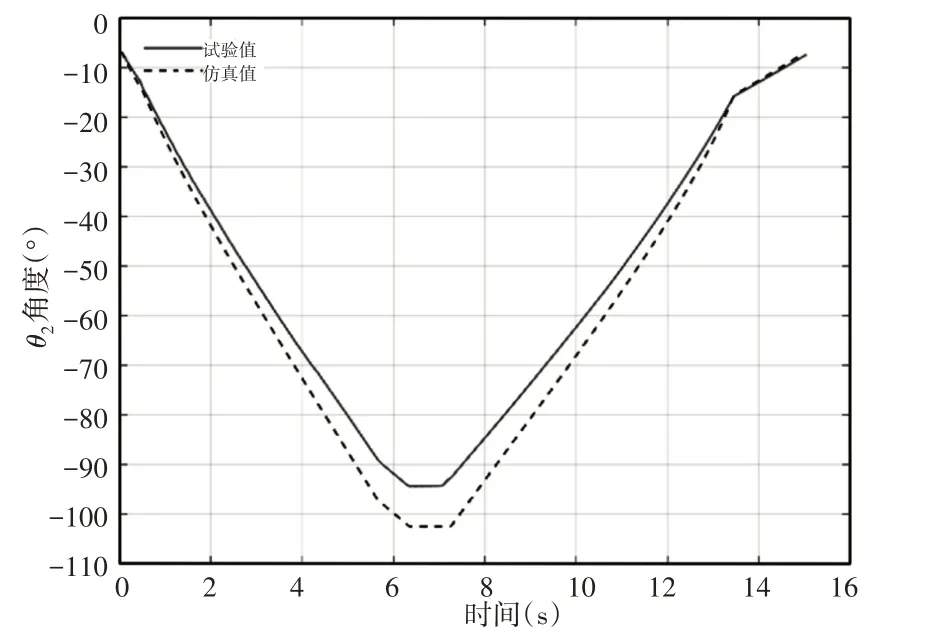
图17 下肢腿θ2角度Fig.17 Lower Limb Leg θ2 Angle

双推杆肢腿机构在双推杆同步驱动时，下肢腿末端运动轨迹是由多段二次函数曲线组成，如图18所示。下肢腿末端运动轨迹从（720，100）开始出发，随双推杆伸长逐渐移动到（320，-480），经过换向后在双推杆收缩下回到初始位置，因双推杆运行时间不同，下肢腿末端运动轨迹是一条封闭的曲线。由于机械结构限制的影响推杆未能到达最顶端，使下肢腿末端运动轨迹的试验值与仿真值存在误差。由表6可知，下肢腿末端运动轨迹曲线试验值与仿真值在X轴方向上的相关系数和误差分别在0.9997和5.10%，在Y轴方向上的相关系数和误差分别在0.9993 和14.20%，表明肢腿机构在Y轴方向更易受到干扰，这与前两种运动工况时的原因相同。

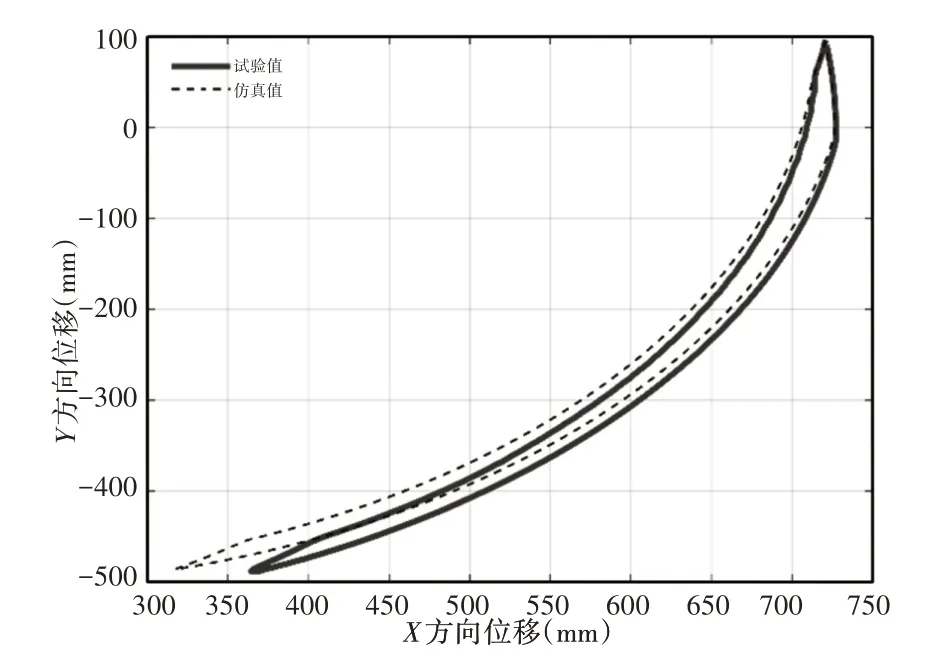
图18 下肢腿末端运动轨迹Fig.18 The Movement Track of End of Lower Limb

双推杆肢腿机构在双推杆同步驱动时，下肢腿末端速度、加速度变化曲线，如图19、图20所示。

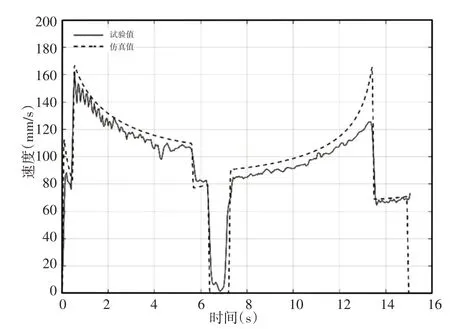
图19 下肢腿末端速度Fig.19 Velocity at the End of Lower Limb

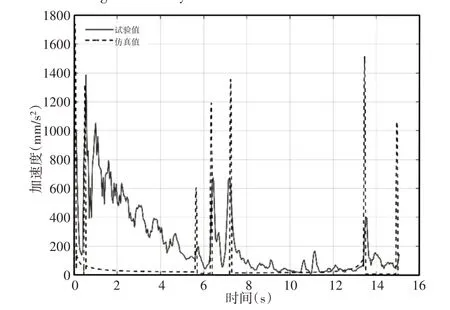
图20 下肢腿末端加速度Fig.20 Acceleration at the End of Lower Limb

下肢腿末端速度在0s、0.4s、5.6s、6.4s、7.2s、13.5s和15s处出现阶跃响应，对应其加速度出现峰值，其中0.4s处的峰值是由于试验过程中一级推杆出现延迟造成的，而5.6s和13.5s处的峰值是由于二级推杆到达最顶端和回到收缩状态造成的，其他峰值出现原因与前两种运动工况相同。另外从图20可知，下肢腿末端加速度试验值与仿真值差异较大，这是因为下肢腿末端加速度是由式（3）经过二次求导得到，在实际测量中双推杆肢腿机构在运行过程中出现振动，导致上、下肢腿相对于X轴方向的角度不断在仿真值上下波动，这种波动经过二次求导后会使下肢腿末端加速度值不同于仿真值。由图19可知，双推杆肢腿机构在双推杆同步驱动下做变速运动，这与图16、图17中得到的结论一致。由表6可知，下肢腿末端速度曲线试验值与仿真值的相关系数和平均相对误差分别为0.9540和13.72%，下肢腿末端加速度曲线试验值与仿真值的相关系数和平均相对误差分别为0.1654 和82.67%。

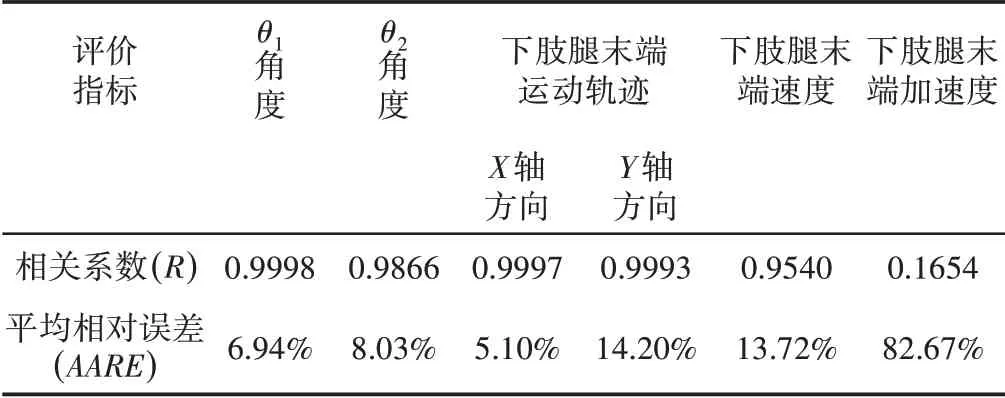
表6 双推杆同步驱动下各参数相关系数和平均相对误差Tab.6 Correlation Coefficient and Average Absolute Relative Error of Each Parameter Under Double Push Rod Synchronous Drive

6 结论

针对双推杆肢腿机构一级推杆独立驱动、二级推杆独立驱动、双推杆同步驱动三种典型运动工况，建立了南极科考机器人双推杆肢腿机构运动学方程，分析了上肢腿和下肢腿相对于X轴方向角度变化规律，下肢腿末端运动轨迹、速度和加速度运动特性曲线，并进行了仿真模拟和试验研究，结论如下：

（1）上肢腿和下肢腿相对于X轴方向角度在三种典型运动工况下呈先减小后增大的变化规律，下肢腿末端运动轨迹是连续二次函数曲线，下肢腿在一级推杆驱动时末端速度为匀速运动，在二级推杆驱动时为变速运动，下肢腿末端加速度在推杆开始伸长和结束收缩时出现峰值，在其他时间段内趋于0值。

（2）对比三种典型运动工况下的仿真值和试验值，可得上肢腿和下肢腿相对于X轴方向角度相关系数在0.95以上，而平均相对误差在16.69%以内；下肢腿末端运动轨迹在X轴方向最大平均相对误差远小于Y轴方向，表明双推杆肢腿机构易受重力影响；下肢腿末端速度的相关系数在0.90 以上，平均相对误差在19.35%以内。