矿用混凝土喷射机齿轮传动多目标模糊优化

曹 阳，马 军，李晓科，路 迪

（1.郑州轻工业大学河南省机械装备智能制造重点实验室，河南 郑州 450002；2.河南北工机械制造有限公司，河南 商丘 476000）

1 引言

在机械传动中，齿轮传动是最主要、也是应用最广泛的一类传动，很多文献对齿轮传动优化进行了深入的研究，出于节约资源，降低成本的目的，这些研究多以齿轮传动的结构优化作为目标[1-4]。然而，现代机械系统是一个与工况环境密切相关的复杂性系统，具有多变量、强耦合及非线性的特点[5]，例如在矿山多粉尘、高温高湿的恶劣工况下，矿用混凝土喷射机齿轮系统不仅受作业空间的限制，而且要有足够的安全平稳性，其约束指标中往往存在大量模糊的因素，它们从完全容许到完全不容许是一个不确定的过渡过程，不考虑这些模糊不确定因素的优化方法是不合理的，因此这是一个必须综合考虑经济性和平稳性的多目标模糊优化问题。针对齿轮传动多目标模糊优化，一般的处理方法是通过模糊规划理论将其转化为多目标确定性优化问题，然后再进一步应用优化算法来进行求解，例如罚函数法、拟牛顿法、复合形法等，这些算法在理论上具有较好的成熟度，但都属于局部优化算法，对于齿轮传动优化问题只能获得局部最优解。

因此后来研究者更多的是将具备一定全局搜索能力的启发式算法应用在齿轮传动优化中，其中，遗传算法以其不依赖梯度信息，具有全局、并行的优化性能而被广泛采用[6-10]，但对于齿轮传动多目标模糊优化设计问题，基本的遗传算法不仅收敛速度有限，而且还难以保证解的全局最优性，需要结合优化模型的具体特点提出有针对性的优化求解方法。

根据矿用混凝土喷射机齿轮传动优化设计模型的多目标、模糊性特点，通过降半梯形隶属度函数和二级模糊评判方法处理模糊性能约束，将多目标模糊优化问题转换为确定性多目标优化问题，在此基础上，提出一种改进的混合遗传算法进行优化求解，并通过与基本遗传算法优化结果的对比，验证其有效性和实用价值。

2 矿用混凝土喷射机齿轮传动多目标模糊优化建模

矿用混凝土喷射机齿轮传动是一个二级直齿圆柱齿轮传动。从减轻质量、节省材料和降低成本的经济性指标考虑，要求该传动系统结构紧凑，这就要求齿轮传动的径向和轴向尺寸要最小，即两齿轮中心距和齿轮分度圆柱体体积最小。同时在齿轮传动过程中经常要正反转，因此尽量小的转动惯量可有效保障传动平稳性。基于上述考虑，矿用混凝土喷射机齿轮传动的优化目标如下：

其中两齿轮中心距：

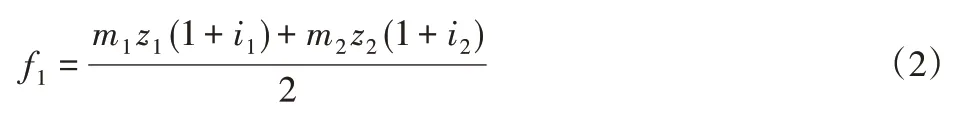
齿轮分度圆柱体体积：

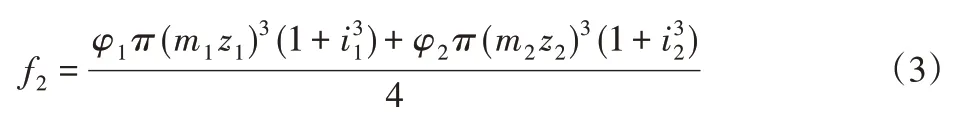
结合文献[10]，传动系统转动惯量：

其中：

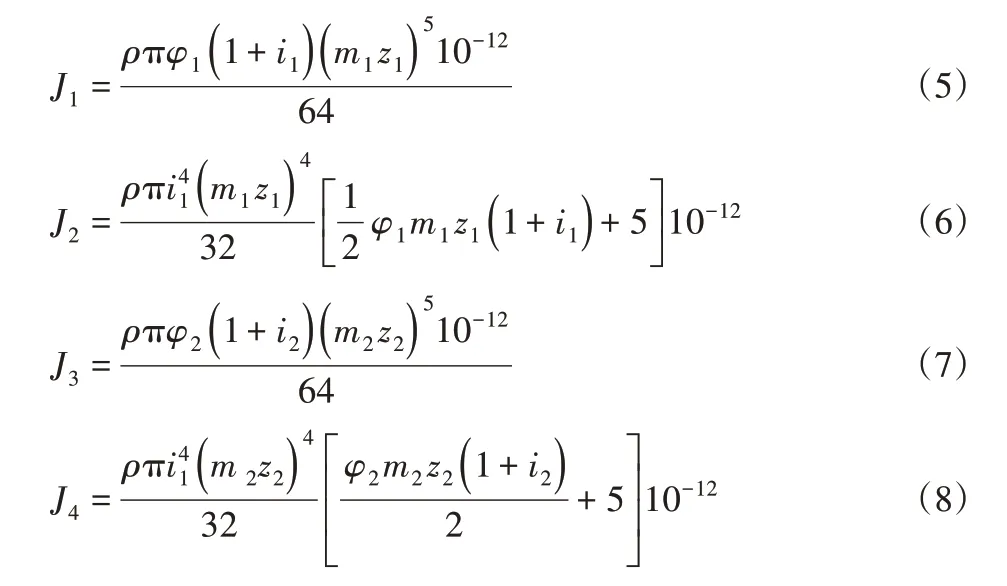
式中：J1、J2、J3、J4—四个齿轮的转动惯量；m1、m2—一、二级齿轮法面模数；i1、i2—一、二级传动比；z1、z2—一、二级的小齿轮齿数；φ1、φ2—一、二级小齿轮的齿宽系数。

考虑到传动系统的平稳性和空间布局，约束条件包含几何约束与性能约束。几何约束包括齿数、模数、传动比和齿宽系数约束。

性能约束包括齿面接触与齿根弯曲疲劳强度约束。矿用混凝土喷射机齿轮传动多目标优化中，准确的齿面接触疲劳许用应力和齿根弯曲疲劳强度很难获得，一般都是模糊的，处于完全许用到完全不许用的中间过程。

①一、二级齿轮齿面接触疲劳强度约束

②一、二级齿轮齿根弯曲疲劳强度约束

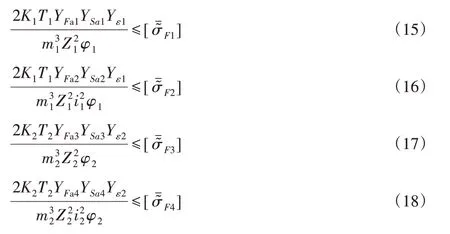
式中：K—载荷系数；T—传递的扭矩；YF—齿形系数；YS—齿根应力修正系数；Yε—重和度系数。因性能约束要考虑约束的模糊性，式中：[σˉ͂H]—模糊许用接触应力；[σˉ͂F]—模糊许用弯曲应力。以上约束条件中引用的符号“～”表示具有模糊性，引用的符号“¯”或“_”表示参数的上或下界。

不失一般性，矿用混凝土喷射机齿轮传动多目标模糊优化模型可以统一表示为求：

3 矿用混凝土喷射机齿轮传动性能约束的模糊性处理

3.1 模糊性能约束的隶属度函数

对于矿用混凝土喷射机齿轮传动多目标模糊优化问题，引入模糊理论来处理性能约束中的模糊性问题，即把齿面接触疲劳许用应力和齿根弯曲疲劳强度约束都处理为一个隶属度函数，从而实现模糊多目标优化模型到确定性多目标优化模型的转化，其原模型约束条件仍严格成立，从而在保证科学性的同时，很好地兼顾了矿用混凝土喷射机齿轮传动设计的经济性和平稳性两个目标。隶属度函数一般要根据问题的模糊性质来具体确定，考虑到齿面接触疲劳许用应力和齿根弯曲疲劳强度的模糊性具有一定的相似性，因此统一采用降半梯形分布的隶属度函数。齿面接触疲劳许用应力和齿根弯曲疲劳强度的隶属度函数uσ(x)，如图1所示。

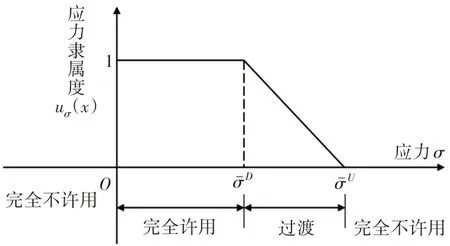
图1 降半梯形分布隶属度函数uσ(x)Fig.1 The Semi-trapezoidal Membership Function uσ(x)

模糊性能约束的隶属度函数表达为：

基于模糊数学分解定律，以一系列水平值截取模糊隶属度函数uσ(x)，可获得不同设防水平下的水平截集λ，即在上式中设：

从上式可得到：

因此，许用应力由水平截集λ的值决定。水平截集λ值越大系统越安全平稳，越小系统越经济。为了使系统即平稳又经济，应寻找一个最优水平值λ*。

3.2 最优化水平截集的模糊综合评价

最优水平值λ*可以采用两级模糊综合评判法来确定。所谓两级模糊综合评价，首先对单个因素进行评判，再对所有因素进行综合评判。

3.2.1 根据设计要求确定影响因素集及每个因素的等级

式中：Sk—第k个影响因素，k=1，2，…，m。因素等级可以表达为sk={sk1，sk2，…，skp}。其中，skl—第k个影响因素的第l个等级。l=1，2，…，p。

3.2.2 根据评判对象的取值范围确定备择集

由于评判对象必然包含在一个区间内，为了通过确定该评判对象的准确值，可以将区间离散化后得到备择集。

式中：Vj—第j个备择集评判子对象，j=1，2，…，n

3.2.3 建立一级模糊评判矩阵

对每一个影响因素进行评判，以确定影响因素对备择集评判子对象的隶属度。设备择集V中第j个评判子对象Vj按因素集S中第k个影响因素Sk评判，Sk对评判子对象Vj的隶属度为γkj，则评判结果可以用评判集合Rk表示，Rk是备择集上的一个模糊子集，则单因素评判集合可表达为：

同理对每个影响因素进行评判，获得单因素隶属度集合，构成因素集的一级模糊评价矩阵：

3.2.4 建立因素权重集

在模糊多目标优化问题中，决策者的评价不仅具有不确定性，还往往具有一定的主观性，各评价因素的重要程度一般是不同的，不可以等同对待。为了反映各个评价因素的差异性，决策者可以对分目标的评价因素进行赋权，即对各个评价指标设置不同的重要度。为反映各个因素的重要程度，对各因素赋予相应权重，权重集为：

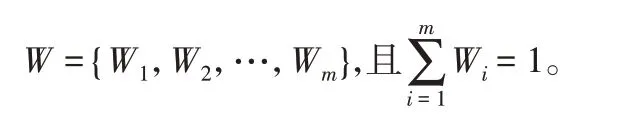
3.2.5 模糊综合评判

综合考虑所有因素对评判对象的影响，获得模糊综合评判集为：

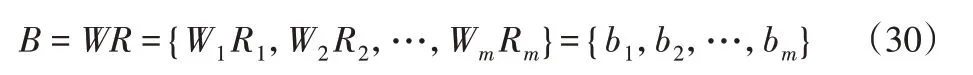
式中：bi—模糊综合评判指标。

最后，用加权平均法得最优水平截集为：

这样就可以将模糊多目标优化问题转化为最优水平截集上的确定性多目标优化问题：

4 面向矿用混凝土喷射机齿轮传动多目标优化求解的混合遗传算法

对有一定复杂约束的优化问题求解，基本遗传算法面临难以快速进入可行域以及难以找到全局最优解的问题。为了在扩大解空间的同时提高求解搜索效率，在基本遗传算法基础上融入局部搜索过程，提出了改进的混合遗传算法，即在混合遗传算法中，将每一代种群中的个体排列顺序打乱，乱序之后种群中的所有个体就都有可能被选中。通过变量迭代和乱序操作方法，（1）增加了种群中所有个体适应度，（2）可以使所有个体被选择的概率均等。该算法步骤，如图2所示。

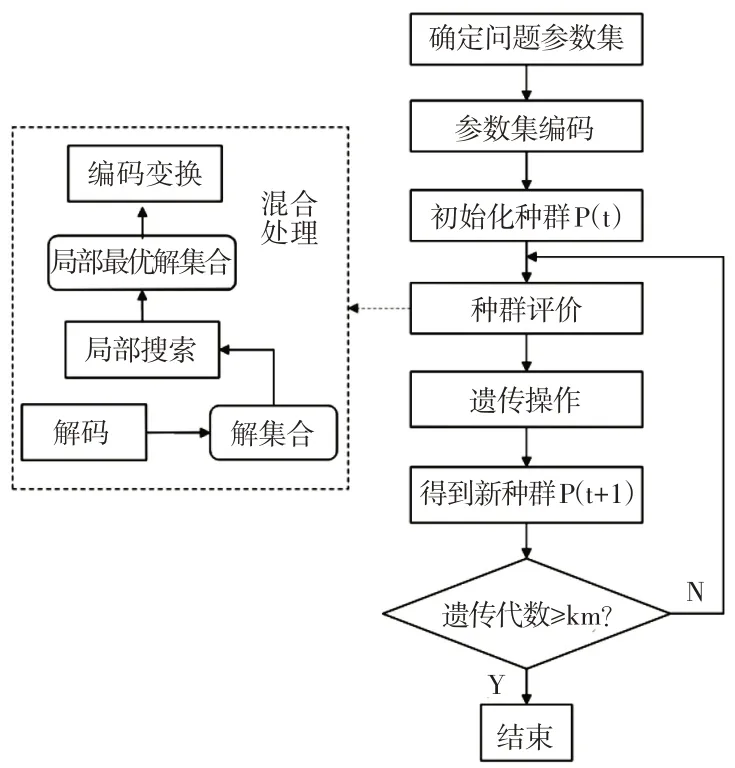
图2 混合遗传算法流程Fig.2 The Flow Diagram of Hybrid Genetic Algorithm

（2）对种群所有个体进行编码，采用二进制编码的方法。

（3）在变量设定的范围内随机产生第一代种群，该种群中的第一个个体为x0。

（4）对种群中各个体进行适应度评价。首先对种群各个体进行解码（采用二进制解码），并求出当前种群中目标函数最小值min(f(x)) 及其对应的个体xb，并将它们保留。令fmin=min(f(x))，xmin=xb；最后对该种群中的各个体适应度函数值进行评价，fs(x)=max(f(x))-f(x)，若max(fs(x)≤κ，则计算结束，否则执行（5）。

（5）按照式（1）进行变量迭代操作，生成新一代种群。

（6）乱序和交叉操作。乱序操作可以通过调用randperm（）函数来完成；采用单点交叉的方式进行交叉操作，即交换两个染色体上随机选定基因位置上的单个基因片段。依照给定的交叉概率pc进行交叉操作。若是多维变量，则基因片段交换的位置是相互独立并且随机的。

（7）按照预先设定的变异概率pb进行变异操作。同交叉操作类似，变异操作也采用随机单点变异，即随机选中个体，再对个体中某一位基因的0、1做更改。若是多维变量，则个体各分量基因变异是独立和随机进行的。

（8）重复（1）到（8），计算达到最大遗传代数km时停止计算，最终输出最优解。

上述步骤中，关键的选择操作按下式进行。

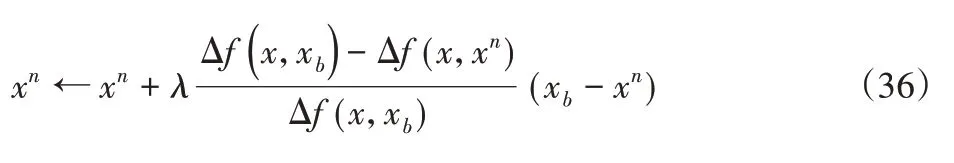
式中：λ—学习因子；xb—目标函数最小（或最大）的染色体。对最小值问题，其适应度值反而越大，以比例选择的角度来说，目标函数值越小，个体就越容易被选中。Δf(x，xb)—最大目标函数差值，且：

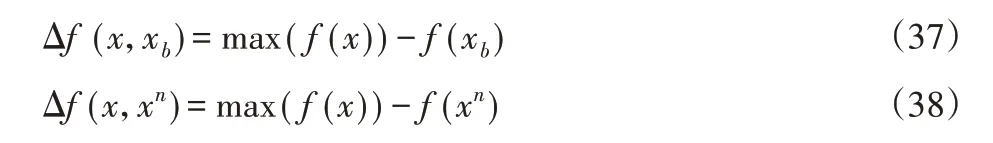
5 实例分析

5.1 模糊性处理

某矿用混凝土喷射机齿轮传动系统在一定强度和刚度条件下，要求传动系统结构紧凑，总体积小，转动惯量小。传动系统主传动功率为5.5kW，输入轴转速960r/min。总传动比i=25。按非对称分布，高速级与低速级的齿宽系数分别为φ1=0.8、φ2=0.8。一级小齿轮45钢调质处理，大齿轮45钢正火处理；二级大、小齿轮都为45钢表面淬火处理。

齿轮传动中两齿轮中心距、齿轮分度圆柱体体积和传动系统转动惯量，受到齿轮的齿数、模数、齿宽、传动比等参数的影响。增加齿数m、模数z和传动比i都可以提高两齿轮中心距，而齿宽增加会增大体积，因此优化设计变量为：

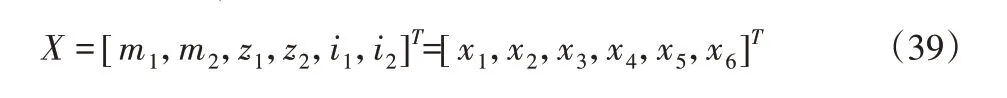
水平截集λ的取值按两级模糊综合评判确定。影响因素及其等级，如表1所示。

表1 因素集与因素等级Tab.1 The Factor Set and Its Grade

由于水平截集λ的取值区间为［0，1］，按步长0.1将其离散后得到备择集V=｛0，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1.0｝。因素权重集为W=｛0.25，0.25，0.15，0.15，0.10，0.10｝。

经过一级和二级模糊综合评判，得到两级模糊综合评判集为：B=｛0，0.061，0.186，0.470，0.560，0.593，0.525，0.403，0.261，0.131，0.040｝。按加权平均求得最优水平值：

将最优水平值λ*代入各模糊性能约束的隶属函数中，获得各性能约束的取值范围，这样将多目标模糊优化问题转化为常规多目标优化问题。

5.2 优化求解

使用混合遗传算法对优化模型进行求解，设种群数量Np=20，二进制编码长度Nb=［8，8，8，8，8，8］，交叉概率pc=0.7，变异概率pb=0.1，最大遗传代数为100，求解后的结果采用合成权重的比较选取一组解，经圆整后为x1=3，x2=3，x3=20，x4=20，x5=4.3，x6=3.7。在种群进化过程中，各个体均向着最优适应度方向进化，直到达到最优适应度。如图3（b）分析可知，随着算法迭代次数的增加虽然最佳适应度均值会有起伏波动，但从全局趋势来看最佳与平均适应的平均值都在稳步下降。

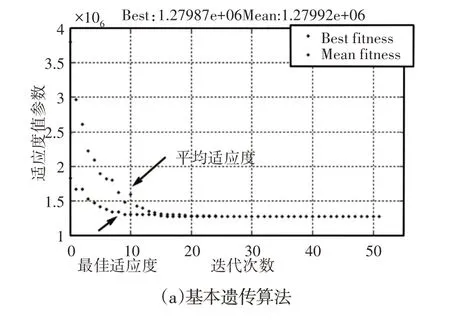
图3 种群中个体平均适应度Fig.3 Average Fitness Values of the Population Individuals

这表明算法的稳定性较好同时可以看出算法的后期收敛速度较慢。对比图3（a）的基本遗传算法，可以看出混合遗传算法的收敛速度要略大一些。

在种群进化过程中，各个体均向着最优适应度方向进化，如图4所示。遗传过程中各局部最优值所对应的个体数量，对比图4（a）、图4（b）可知，混合遗传算法中最优适应度值区间中个体数量也要高于基本遗传算法。

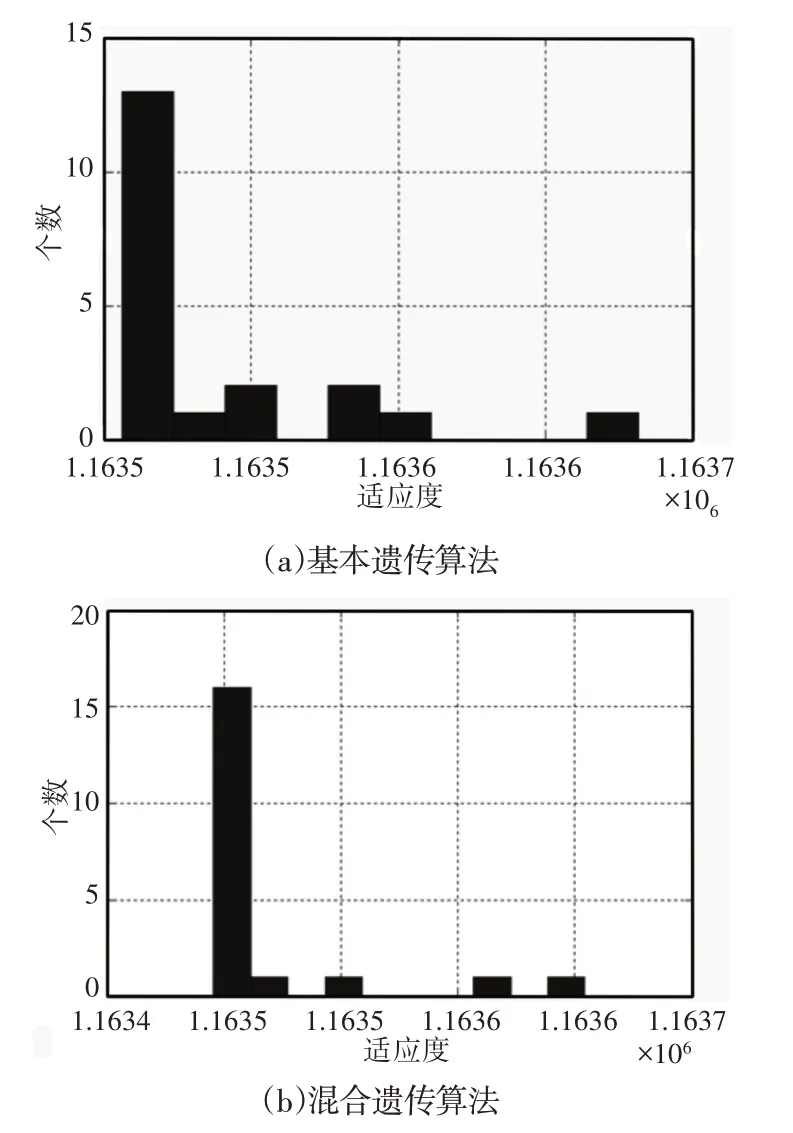
图4 各局部最优适应度对应种群个数Fig.4 The Population Size According to the Local Optimal Fitness Degree

将结果与遗传算法得出的结果，如表2所示。从优化的结果可以看出，采用的混合遗传算法，其中心距减少16%，齿轮总体积减少32%，转动惯量减少27%，优化效果较显著。

表2 优化结果对比Tab.2 The Comparison of the Optimization Results

6 总结

（1）采用降半梯形分布模糊隶属度函数和两级模糊评判法，可以有效的将矿用混凝土喷射机减速器齿轮传动设计模糊优化模型转化为确定性优化模型。

（2）在优化模型的求解方面，对比基本遗传算法，改进后的混合遗传算法稳定性较好，收敛速度更快，而且更接近全局最优解。

（3）采用混合遗传算法，优化后的矿用混凝土喷射系统其中心距减少16%，齿轮总体积减少32%，转动惯量减少27%，结构更紧凑，经济性和平稳性更优。