光储混合直流微电网非线性分层控制策略

胡荣辉，祁寿贤，张怡雪，张 晶，张玉勇

（1.青海综合能源服务有限公司，青海 西宁 810008；2.烟台东方威思顿电气有限公司，山东 烟台 264003）

0 引言

在光储混合的直流微电网中光伏出力间歇性以及负荷的随机波动不可避免的会对直流母线电压产生影响［1-2］。因此，采用合适的控制策略来保证直流母线电压的稳定，维持系统的功率平衡至关重要［3-4］。

当前直流微电网的控制策略以PI控制和线性二次型调节器控制为主［5］。文献［6］提出了一种基于电压PI 闭环加移相控制的双向全桥DC/DC 控制方式，能够针对直流微电网的母线电压波动做出快速响应。文献［7］提出了一种基于PI控制和高通滤波器相结合的控制策略，它能抑制微源和负荷波动对直流母线电压的影响。这些控制方法虽然能取得不错的效果，但在一些复杂情况下却难以奏效。主要原因是这些方法往往针对不同的对象采用了相同的控制方式，而忽略了不同功率单元的差异性以及它们之间的相互联系。因此，当直流微电网内的微源的出力发生突变或负荷急剧变化时，系统难以快速恢复稳定，甚至会因缺乏灵活的协调控制机制而加剧这种不利影响。

为了提高直流微电网稳定运行能力，一些专家提出针对不同的功率单元进行分别控制，并采用分层控制思想对整个系统进行协调控制［8-9］。为了实现直流微电网内部功率的协调运行，文献［10］提出了一种包含三层控制结构的多代理控制方案，能够实现微电网内部各类微源与储能设备以及微电网与邻近配电网的功率分配。文献［11］通过对直流微电网运行模式的划分，提出了一种基于下垂控制的能量均分策略，可实现微电网内部光伏阵列和储能单元的协调自治。文献［12］则提出了一种基于自适应下垂控制的分层控制策略，该方法能够根据不同储能设备的最大功率自动分配负荷功率，有效提升了微电网的稳定运行能力。虽然上述的分层控制策略具有较好的灵活性和可行性，但也存在局限性。直流微电网中大量使用的电力电子装置具有很明显的非线性特性，上述的分层控制方法主要基于线性理论而设计，因而大多数时候难以达到令人满意的效果，而只能在平衡点附近保持相对的稳定［13］。

针对线性分层控制方法的不足，设计了一种光储混合直流微电网的非线性分层控制方法。该方法的顶层控制通过对各功率单元协调来维持直流母线的电压稳定，同时为底层各功率单元的控制提供参考电流。底层控制则采用非线性控制策略分别对光伏阵列，蓄电池以及超级电容器的输出电流进行控制。该方法充分利用超级电容器和蓄电池的动态特性，能够在不同时间尺度上保障直流母线电压的稳定。为了验证所提非线性控制策略的稳定性，推导了各功率单元及整个系统的李雅普诺夫函数，对各控制系统的稳定性进来了理论验证，并给出了相关的控制参数计算方法。基于MATLAB/Simulink 仿真平台搭建了光储混合直流微电网仿真模型对所提控制策略进行了验证。仿真证明在负荷突变和光伏出力波动时，所提控制方法能够有效地维持直流母线电压的稳定，相比传统的PI控制方法，所提的非线性分层控制法响应速度更快，调节效果更好。

1 直流微电网的结构与工作原理

所研究的直流微电网的结构如图1 所示，直流微电网中包含了光伏阵列、蓄电池、超级电容器以及等效负荷。

图1 直流微电网简化结构

该直流微电网中的光伏阵列、蓄电池和超级电容器通过三相DC/DC 升压电路将连接到直流母线。其中的3 个DC/DC 升压斩波电路包含了6 个并联的开关，这些开关由3 个不同的占空比独立控制。通过对不同开关占空比的调控可以实现光伏阵列，储能设备和负载之间的电能交换。该直流微电网内的脉宽调制数学模型如式（1）所示。

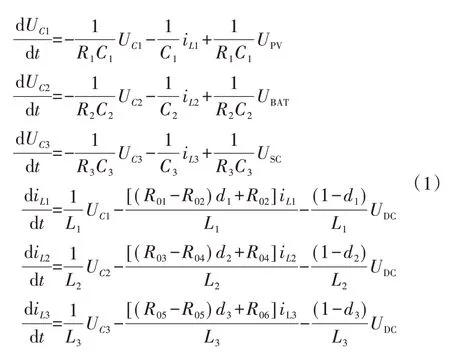
式中：Ri、Li、Ci（i=1，2，3）分别为已知的电阻、电容和电感；R01—R06为开关的内阻；RLoad为等效负荷；UC1、UC2、UC3为各电容的电压；iL1、iL2、iL3为电感电流；UPV、UBAT、USC、UDC分别为光伏、蓄电池、电容器和直流母线的电压；d1、d2、d3为不同的占空比，通过对它们的调节可实现对功率的控制。

由图1 可知储能系统的主要功能是维持系统的功率平衡，一方面需要在光伏发电大于负荷需求时，存储多余的电能；另一方面也需要在光伏出力不足或不出力时为负荷提供电能。若用PST、PBAT、PSC分别为混合储能系统、蓄电池以及超级电容器的输出功率，用PDC、PPV、PLoad分别表示直流微电网与外部电网的交换功率，光伏阵列输出功率以及负荷消耗的功率，则可以推导出直流微电网内的功率平衡关系如式（2）所示。

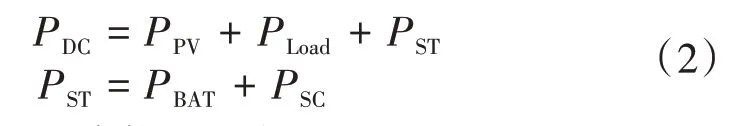
对式（2）进一步推导可得：

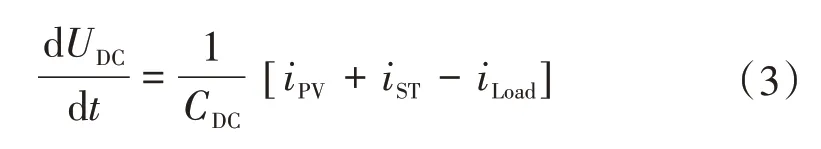
式中：iST为混合储能系统的输出电流；iLoad为负荷电流；CDC为直流母线等效电容。根据式（3）可知，直流母线的电压波动受到光伏、混合储能系统和负荷电流的影响。但负荷电流是不可控的，故而只能通过对光伏阵列以及混合储能系统的电流进行控制来实现稳定系统功率平衡，维持直流母线电压稳定的目的。若忽略开关的内阻，则式（3）可进一步简化为

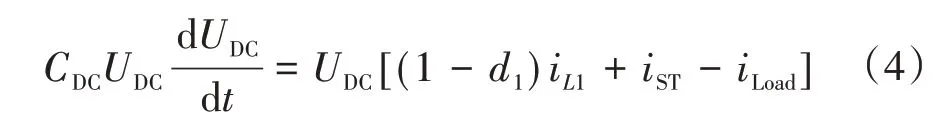
为了方便分析，本文假定蓄电池和超级电容器的初始荷电状态维持在［0.2，0.8］区间范围，即其处于线性工作区域［14］。

3 控制系统结构

采用模块化的控制策略设计控制框架。顶层控制主要通过对底层各系统之间进行协调来保证系统的功率平衡；底层则为各子系统内部的控制。针对光伏阵列设计了两种控制方式，恒压控制和最大功率追踪（Maximum Power Point Tracking，MPPT）控制，储能系统则包括了充电、放电和休眠3种模式。图2给出了所研究的直流微电网顶层控制逻辑，可以发现该直流微电网主要包含了3种工作模式：光伏采用MPPT 控制且储能系统放电；光伏采用MPPT 控制且储能系统充电；光伏采用恒压控制且储能休眠。

图2 顶层控制逻辑

直流微电网的底层控制包括了直流母线的电压控制、光伏的输出电流控制以及混合储能系统的充放电控制。图3 给出了直流微电网的底层控制框图，图中为光伏控制的内环参考电流为蓄电池参考电流为超级电容器参考电流，U为直流母线参考电压，U为光伏阵列的参考电压。可以看出光伏阵列包含了MPPT控制和恒压控制两种方式。采用MPPT 控制模式时，通过MPPT 为光伏阵列提供参考电压U，使光伏阵列始终以最大功率发电；当采用恒压控制时则通过直接给定的电压参考值U作为光伏电压控制的参数。经过光伏的电压控制可以为光伏并网电流提供参考值。

图3 底层控制策略

针对储能系统的控制则需要考虑不同储能设备的充放电特性和它们的状态进行协同控制。由图3可知储能系统采用了外环电压与内环电流相结合的方式进行控制，外环的电压控制主要用于对直流母线电压的追踪，内环的电流控制则用于对储能设备的充放电进行控制用于维持系统的功率平衡。其中蓄电池和超级电容器的参考电流可以通过如图4 所示二阶低通滤波器来确定［15］。图中为混合储能系统的参考电流，TSC和TBAT分别为超级电容器和蓄电池的时间常数，且满足TSC＞TBAT。TSC和TBAT的值可根据功率波动的频谱图分析，参考文献［16］所提方法可知光伏功率波动主要集中在0.01～0.5 Hz，若以此为基础，通过考虑蓄电池和超级电容器的充放电极端情况，可以将时间常数设置在0.001～0.05 范围内。当确定了超级电容器和蓄电池的时间常数，则可以进一步确定对应低通滤波器的截止频率fSC和fBAT。

图4 二阶低通滤波控制

根据图4 得到蓄电池和超级电容器的参考电流与储能系统输出电流的关系为：

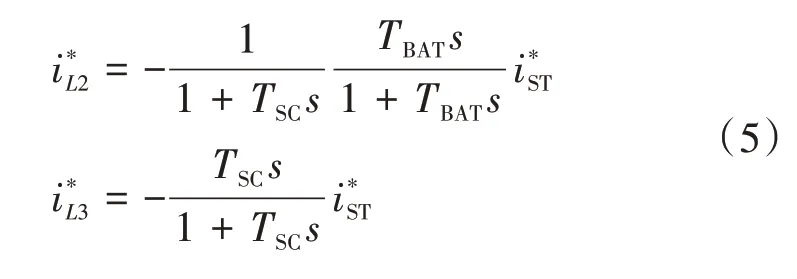
4 非线性控制策略

4.1 光伏电流控制

为了满足系统的功率平衡，并尽可能充分利用太阳能发电，对光伏阵列设置了两种控制模式：最大功率追踪控制和恒压输出控制，恒压控制仅当PPV≥PLoad+PST时采用。电导增量法是通过比较光伏阵列的电导增量和瞬间电导来改变控制信号［13］，根据光伏输出特性曲线可知光伏发电的最大功率点满足

根据式（6）可以得到电导增量法的流程如图5所示。光伏的恒压控制则是令光伏的实际输出电压UPV追踪直流母线参考电压来保证直流母线电压的稳定。无论采取何种控制方法，将得到光伏输出电压与直流母线电压参考值作差，并将差值作为光伏输出控制的参考电流。

图5 电导增量法流程

结合图1和图3可知，在光伏底层控制种的是通过控制占空比d1实现对UC1和iL1的动态调控，结合式（1）可知

则可推导光伏阵列输出电压和电流的eVC1，eiL1的动态模型：

式中：αPV为积分项，用来保证UC1和iL2之间的稳态误差为零；KPV、KαPV为增益系数。

根据式（7）—式（9）可得到和d1的控制方程为：

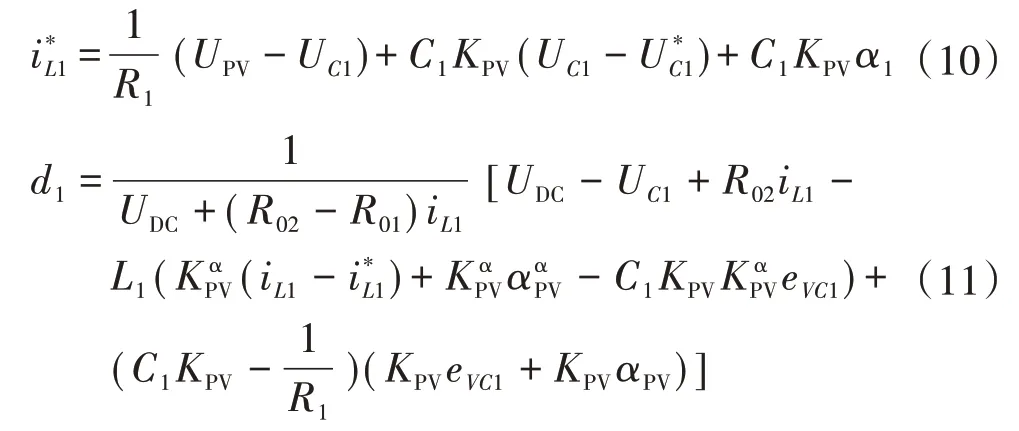
根据控制方程可知通过占空比d1的控制可以实现光伏输出电流的非线性控制。

4.2 蓄电池控制

通过对占空比d2调节可以实现对储能系统的充放电电流进行控制，根据式（1）可知：

进一步，引入蓄电池累积误差平衡因子αB，通过反推可得到蓄电池电流动态模型。

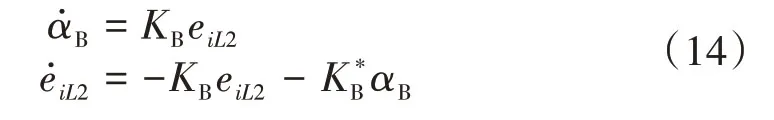
式中：KB、均为蓄电池增益系数。结合式（12）—式（14）可推导d2的闭环传递函数为

4.3 超级电容器控制

通过对占空比d3的调节可以实现对超级电容器充放电的电流控制，根据式（1）可知：

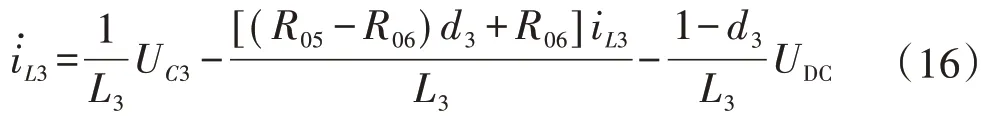
定义其误差为

同样通过引入累积误差平衡因子，可以反推得到超级电容器的误差电流小信号为：

式中：αS为超级电容器累积误差平衡因子；KS为超级电容器增益系数。结合式（16）和式（18）可知占空比d3闭环传递函数为

4.4 直流母线的电压控制

如图1 所示，外部的电压回路用于控制直流母线的电压稳定，在给点参考电压情况下，直流母线的电压误差为

引入直流母线累计误差平衡因子αDC，则直流母线电压UDC的动态模型为：

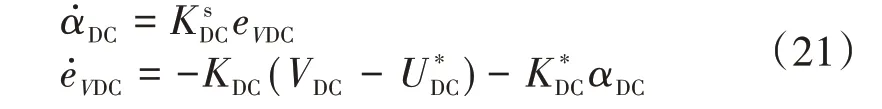
根据式（22）可知对直流母线电压的闭环控制实际上仍是对光伏系统输出电流iL1和储能系统输出电流iST的控制。进一步，对式（22）进行变形可知直流母线电压的小信号模型为

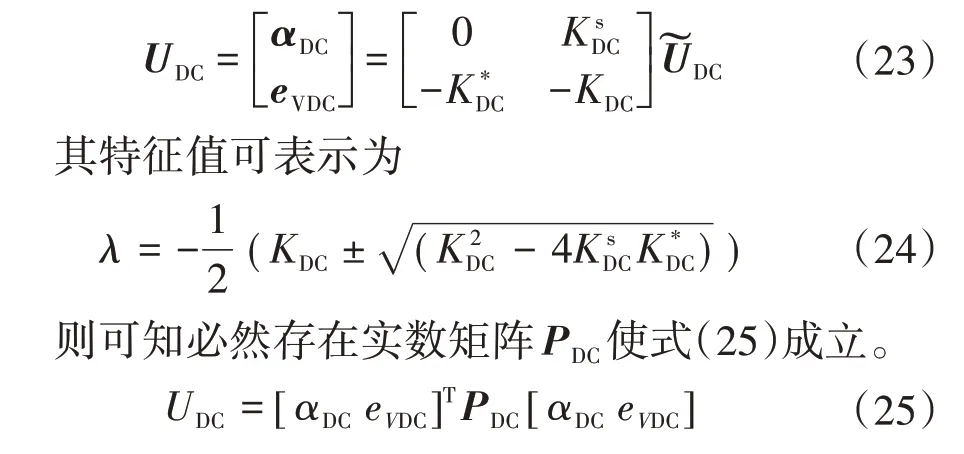
进一步推导可知必然存在实数矩阵x满足以下关系：

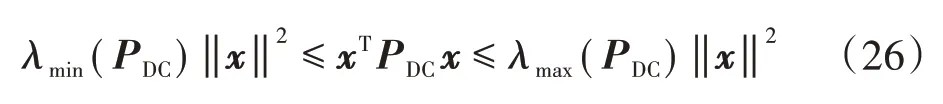
因此，可知直流母线电压满足式（27）的关系，式中mDC为正实数。

该结果说明直流微电网直流母线电压的闭环控制回路满足指数稳定关系。

4 系统稳定性分析与参数设置

4.1 系统的稳定性分析

根据上述的推导可知UC1，iL1，iL2，iL3，UDC是受控变量，可以通过对占空比的控制进行调节。UC3和UC3为非受控变量，它们的值不能直接通过对占空比调节进行控制，但由式（1）可知UC2和UC3达到其平衡点则可以推导出它们与的关系如式（29）所示。

定义UC2和UC3的误差为

则结合式（1）、式（10）、式（12）、式（16）和式（29）可推导出不同开关之间电压的李雅普诺夫函数为：

式中：U1，2、U3，4、U5，6分别为对应了光伏系统的输出电压，蓄电池两端输出电压以及超级电容器两端的输出电压。通过对式（31）化简可以进一步推导上述开关电压的李雅普诺夫函数的一阶导数为：

根据式（34）可知整个直流母线电压的状态满足指数收敛条件，因而整个系统是稳定的。

4.2 参数设计

为了实现较好的控制效果，有必要对参数进行优化。一种简单可行的参数优化方法是基于给定的期望来推导系统的传递函数。以光伏输出控制为例，若令则，系统的闭环传递函数可表示为

需要注意的是图3 所示的电压控制和电流控制的时间常数是不相同的，通常情况下电流控制器的调节速率更快。本文根据经验设置62.83 rad/s，ςDC=0.7。将其带入式（37）即可求的直流母线电压控制参数=3 947.6和KDC=11.09。

对于光伏输出控制，蓄电池控制以及超级电容器的控制均可采用同样的原理进行设计。令光伏输出控制回路的参数，可推导出KPV=68.7；令蓄电池输出控制回路的参数，则可以推导出KB=89.6；令超级电容器输出控制回路的参数，则可以推导出KS=6 283。

5 仿真验证

基于MATLAB/Simulink 搭建图6 所示的直流微电网仿真模型验证所提控制策略的有效性。如图6所示，该模型包括了光伏阵列，蓄电池和超级电容器组成的储能系统和等效负荷。其中光伏发电单元采用MPPT以保证其始终以最大效率发电，蓄电池和超级电容器可独立控制。仿真验证的目的是证明所提出的控制策略可在光伏出力波动和负载突变的情况下，能够通过对蓄电池和超级电容器的充放电维持系统直流母线电压的稳定。仿真模型的主要参数的值如表1 所示。系统中采用的二阶低通滤波器分别对应蓄电池的输出电流和超级电容器的输出电流。考虑混合储能系统的极端运行情况，对蓄电池和超级电容器的时间常数进行设计，设计的蓄电池时间常数为0.05，超级电容器时间常数为0.005，则对应蓄电池的截止频率为20 Hz，超级电容器截止频率为2 000 Hz。

图6 直流微电网仿真模型

表1 直流微电网参数

图7 展示了部分仿真曲线，从上到下依直流母线电压UDC、负荷电流iLoad、光伏阵列输出电流iPV、蓄电池实际输出电流iBAT及其参考电流、超级电容器的实际输出电流iSC和参考电流。仿真过程中设置系统的初始时刻的负载电阻为10 Ω，光伏阵列的辐照度为1 000 W/m2，蓄电池和超级电容器的初始核电荷数均为0.5，直流母线电压为50 V。在0.06 s＜t＜0.65 s 时使负载减小到10 Ω。并；在0.22 s 时使光伏阵列的辐照度突然下降到200 W/m2，当t＞0.46 s时使太阳辐照度恢复到1 000 W/m2。可以看出，当负载或太阳辐照度发生变化时，直流母线电压也随之发生变化，但在储能系统的调节下很快又恢复到稳定值（50 V）。而且，根据仿真模型的示波器可以看出系统的响应时间为10 ms，最大的直流母线电压偏差等于0.08 V。

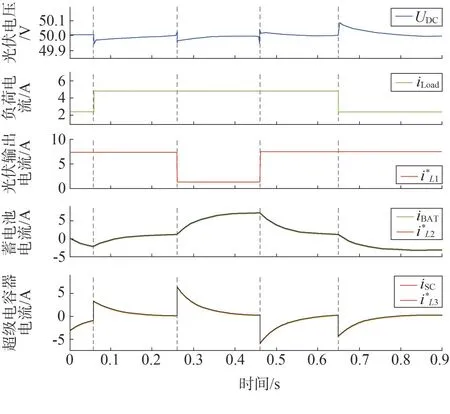
图7 系统动态响应曲线

此外，观察蓄电池输出电流和给定的参考电流，可以看出上层控制给出的参考电流缓慢变化时，蓄电池输出电流也跟随着参考电流变化，而且蓄电池的纹波也较小。从超级电容器的电流变化趋势也可以看出，当太阳辐照度或负载发生变化，超级电容器的电流的实际值和参考值迅速发生变化，说明超级电容器具有快速响应能力，能够在较短时间内对直流母线电压进行调节。但随着时间的推移，超级电容器的电流逐渐减小到零，在这个过程中蓄电池的输出电流则是逐渐增大，并在后续较长时间内维持系统的功率平衡和直流母线电压的稳定。上述结果证明了本文所提出的非线性分层控制策略在光储混合直流微电网控制方面的有效性。

为了证明所提出的非线性分层控制策略比传统的PI 控制效果更好，基于同样的仿真模型，采用PI控制进行对比验证。图8 给出了基于PI 控制的仿真结果，其中的从上到下第一幅图展示了不同控制策略下的直流母线电压波动曲线，其中采用PI 控制的直流母线电压曲线为蓝色，采用非线性分层控制的直流母线电压曲线为红色。可以发现虽然两种控制策略都能保证直流母线电压最终能够稳定在50 V，但基于PI 控制的直流母线电压最大波动为1.2 V，远大于采用非线性分层控制的直流母线电压的波动。此外，两种控制方法的响应时间也不同，PI控制的直流母线从波动到最终稳定大约耗时60 ms，大于本文所提出的控制方法用时。

图8 基于PI控制的系统动态响应曲线

对比图7 和图8 中蓄电池和超级电容器响应曲线，可以发现两种控制策略下蓄电池的输出电流曲线基本相同，均能够随着给定的参考信号缓慢变化，在较长的时间范围内维持系统直流母线电压的稳定。然而，两种控制策略对应的超级电容器的电流响应有明显的区别。当光伏出力和负载突变时，采用PI控制策略的超级电容器的输出电流会有明显的振荡，这种振荡使得直流母线电压而产生了明显的波动。而采用本文所提的非线性分层控制策略则能避免这种情况的发生。可见本文所提方法相比传统的PI控制更有优势。

6 结语

针对传统的线性控制策略无法有效应对直流微电网内因光伏出力突变或负荷突变引起的直流母线电压波动的不足。提出了一种直流微电网的非线性控制方法，该方法以分层控制的思想设计控制框架，通过上层控制器实现系统各组件之间功率平衡优化，底层则采用非线性控制方法来确保在各功率单元在复杂运行条件下的参数稳定，通过上下层级之间的协调能够保证系统在不同时间尺度下的稳定运行。与此同时，本文还将系统内不同控制变量的小信号模型与李雅普诺夫函数相结合对整个系统的动态稳定性进行分析，理论推导了本文所提方法能够保证系统的动态稳定。基于MATLAB/Simulink 的仿真也验证了本文所提的方法相比于传统的线性控制方法具有更好的控制效果。