分段式磁响应软连续体机器人的设计及仿真*

倪阳阳，李木军

(中国科学技术大学 精密机械与精密仪器系，安徽 合肥 230026)

软连续体机器人(CR)是一种具有高灵活性的新型生物启发机器人，它的最初设计来源于象鼻和章鱼触手等无脊椎动物的生物器官[1-3]。不同于传统的刚性机器人，它们具有柔软、高度非线性变形和环境适应性强等特点，非常适用于对精度和安全性要求很高的非结构化环境。一方面，它们采用柔软的材料来改善人机界面的阻抗匹配；另一方面，各种灵活的驱动方法，如肌腱、流体和智能材料驱动等赋予了它们更加新颖的功能。近年来，随着软连续体机器人规模的不断变化，关于它们在生物医学领域中的应用研究层出不穷[4-6]。传统的肌腱、流体驱动方式由于结构复杂度高、控制精度低以及驱动迟滞等缺点而受到严重限制，兼具小型化和远程控制优势的磁响应软连续体机器人的出现很好地解决了上述问题[7-8]。

早期的磁响应软连续体机器人主要通过在软聚合物基体中嵌入微型磁铁的方式制作而成，它们通常被用作外科手术中的可操纵导管，在磁导航系统或磁共振成像(MRI)系统的驱动下被远程引导至目标位置[9]。Choi等[10]提出了一种新颖的磁控软微型机器人系统，他们将由硅橡胶基体、2个永磁铁和1个微弹簧组成的磁响应尖端连接到导丝头部，并通过驱动磁场直接控制尖端的转向来操纵和引导整个导管。即便如此，这类磁控导管的小型化仍受到嵌入磁铁尺寸的限制，难以拓展到更狭窄的操作环境，且存在磁铁在术中脱落的风险。因此，相关研究人员提出了一种亚毫米级铁磁软连续体机器人[11]，能够实现磁场下的主动和全方位转向以及在高度受限的环境中的导航。它的磁极性由均匀混合在软聚合物基体中的磁性颗粒(NdFeB)产生，通过磁性颗粒在外部磁场下受到的扭矩激发内应力，从而诱导机器人的弯曲变形。此外，他们还研究了这类材料在磁场下的变形规律[12]，并在ABAQUS有限元仿真软件中开发了专用于分析硬磁软材料的用户单元子程序UEL，这为更方便地分析该材料体系下任意复杂结构的变形以及机器人的形状可编程性研究提供了理论基础。

本文以用于介入式治疗的铁磁软连续体机器人为原型，提出并设计了能够在驱动磁场下完成二维预定义轮廓的分段式磁响应软连续体机器人。根据硬磁颗粒在磁场下受到磁力矩而诱导变形的基本规律，能够对预定义变形下的连续体机器人分段并对每一段的磁化模式进行初步设计。随后，基于ABAQUS的二次开发功能对预设计的连续体机器人进行建模、仿真，仿真结果表明，分段式磁响应连续体机器人能够很好地达到预定义轮廓。在此基础上，分别研究了磁性颗粒含量以及机器人的长径比对驱动性能的影响，变形程度越大说明驱动性能越好。这项研究一方面拓展了铁磁软连续体机器人的形状可编程性能，另一方面基于对上述2个变量的仿真分析也推进了对分段式磁响应软连续体机器人驱动性能的优化设计。

1 材料与方法

1.1 硬磁软材料

磁响应软连续体机器人属于基于智能材料驱动的机器人[13-14]，通过磁性材料中的磁偶极子在外加磁场下表现出的趋于磁场方向转动的特性诱导机器人整体的弯曲。以往对磁响应软材料的研究主要集中在由顺磁性材料或软磁性材料制成的弹性杆或梁上[15-16]，对硬磁性材料的研究还处于起步阶段。考虑到顺磁性材料在充磁后无法保留剩余磁化，而软磁性材料由于矫顽力较低导致剩磁很容易被驱动磁场还原，由软磁性材料制作的连续体机器人只能产生简单的伸缩变形。因此，研究者们将具有高矫顽力的硬磁性材料引入磁响应软连续体机器人中，使得机器人能够在较大的外加磁场范围内被驱动为更复杂化、多样化的形态，进一步拓展了磁响应软连续体机器人在非结构化环境中的应用。

本文中的硬磁软材料由dragon skin弹性体基质和磁性颗粒NdFeB组成，图1所示展示了它的微观结构及充磁前后材料的状态变化。假设要给图中的磁响应软连续体机器人赋予沿轴向的磁化模式，那么通过对其施加足够大的轴向充磁磁场，机器人内部的磁偶极子就会在磁力矩的作用下逐渐转向至最终沿轴向均匀排布。当撤去外加磁场后，磁性颗粒的高矫顽力使得它们具有较高的剩余磁化强度而仍能够保持轴向分布的状态。假设材料体是均匀、各向同性且不可压缩的，施加的匀强磁场将对磁化域中的磁性颗粒产生磁矩W(见图2)，磁效应下的柯西应力张量为：

σmag=(M×B)·F

(1)

同时，连续体机器人的变形将产生弹性柯西应力，对于总柯西应力，满足如下方程：

div(σ)+fg=0

(2)

式中，fg是每单位体积的力矢量，等同于应力张量中的磁力。在合理的边界条件下求解变形梯度张量，从而得到磁响应软连续体机器人在磁场下的变形，如下述公式所示。

(3)

式中，δ为挠度；L、D分别为连续体机器人的长度和直径；G为材料的剪切模量。

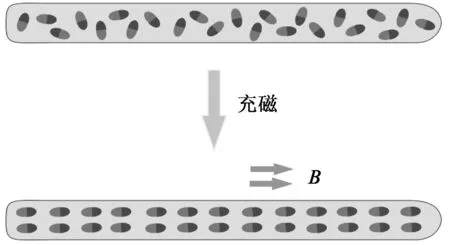
图1 材料的充磁示意图

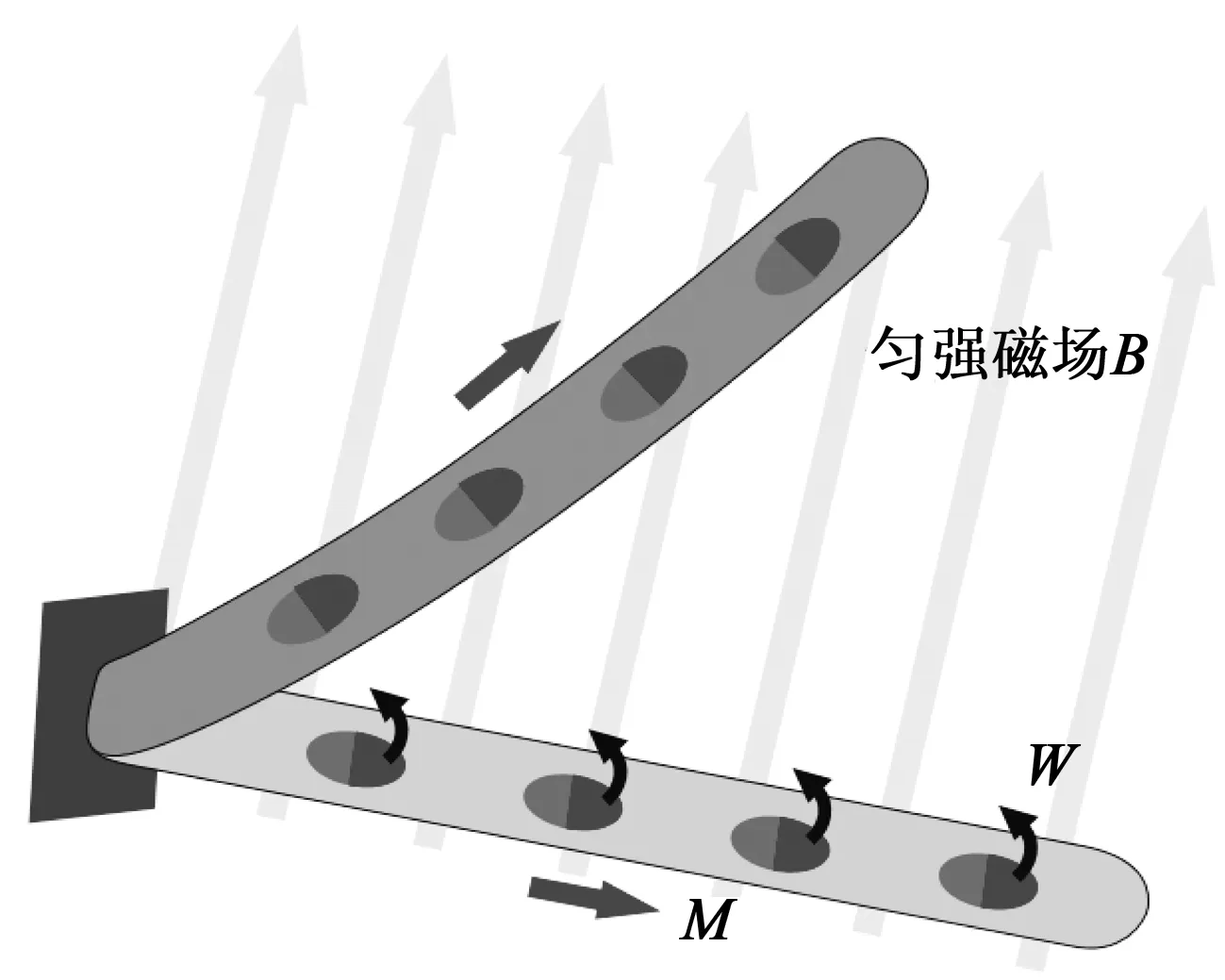
图2 磁响应尖端在匀强磁场下的变形示意图

1.2 基于ABAQUS二次开发的有限元仿真

ABAQUS是一款功能强大且适用性很强的有限元仿真软件，它通过提供各种用户子程序接口以方便用户根据个人需求编写具有定制化功能的有限元分析程序，这属于ABAQUS求解器层次的二次开发应用。ABAQUS有限元分析就是对多自由度系统的运动微分方程组的求解过程，通过网格划分将复杂的体系离散为有限个单元和结点并保证每个单元及结点处受力平衡，在这一过程中，采取的单元类型将直接影响求解结果。由于ABAQUS自带的单元库没有符合本文中硬磁软材料的单元类型，此时需要用户编写自定义单元，创建新的单元类型。

本文基于研究人员已经开发并公开的用于硬磁软材料在磁场下的有限元仿真分析的用户单元子程序UEL，采取生成模型输入数据文件并关联UEL的方式进行仿真分析。其中，模型输入数据文件，简称inp文件，是ABAQUS的执行文件，它包含一个分析作业的完整信息，主要有结点、单元和网格信息、材料属性、边界条件、外加场定义等。需要注意的是，inp文件中默认的单元类型关键字应修改成自定义单元以实现与自定义单元的关联。基于inp文件仿真分析方法的最大优势在于可以通过直接修改文件中的相关信息对作业进行调整，避免了重复建模、定义参数等操作过程。

2 磁响应软连续体机器人的设计

2.1 分段结构

将连续体机器人划分为若干段并对每一段的执行机构进行单独设计，不但能使连续体机器人的结构和变形模式更加灵活和多样化，也进一步拓宽了它们的应用场景。已有大量研究工作[17]证明了这种分段结构的优势和意义，Kim等[18]设计了一种由3段相互连接的内弹簧和1个连续的长外弹簧组成的连续体机器人，并通过机器人中心轴附近的肌腱结构实现独立的分段控制。目前关于磁响应软连续体机器人的分段结构研究还有待进一步挖掘和深入探索，比如通过分段实现机器人的优化设计、形状可编程等。已有研究人员基于对嵌入三块微型磁铁的磁响应触手机器人的有限元仿真实现了触手在驱动磁场下的预定义轮廓，但还没有调研到与由硬磁软材料制作而成的分段式磁响应软连续体机器人的设计及驱动性能研究相关的工作。

2.2 几种变形形态下的磁化设计

硬磁软材料对磁刺激的响应主要表现为：外加磁场通过作用在磁偶极子上的磁力矩激发内应力，在这一过程中，磁偶极子将由初始状态向磁场方向偏转从而引起整体的弯曲变形。根据这一基本变形规律，可以通过对磁响应软连续体机器人的分段及磁化模式设计大致实现它们在磁场下的预定义变形。首先，规定了几种典型的曲线变形态，包括U型、弦线型以及W型。然后，根据这几种形态的对称及弯曲特征将它们分为若干段(见图3)，U型可以简单地分为对称的两段；弦线型从左到右可以等分为上升段1，下降段1、2和上升段2；W型则可以等分为下降段1、上升段1以及下降段2和上升段2。

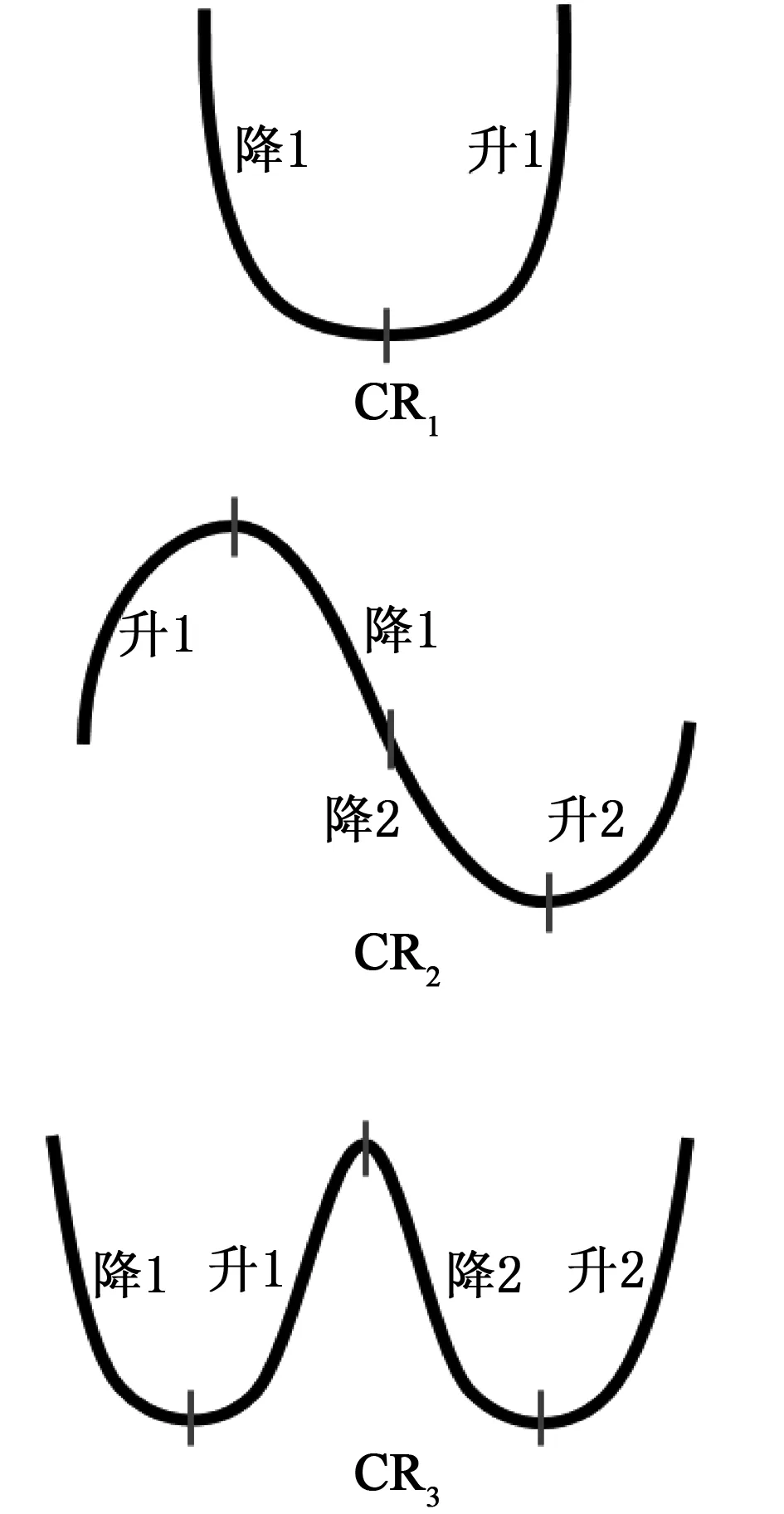
图3 变形形态的分段示意图

上述预定义形态的划分实际上是对磁响应软连续体机器人的分段定义过程，U型、弦线型和W型分别对应两段式、四段式和四段式磁响应软连续体机器人。在此基础上，需要进一步设计每一段的磁化模式(见图4)。假设驱动磁场B是沿着y轴正方向，大小为50 mT的恒定匀强磁场，磁响应软连续体机器人在初始态下的轴向沿着x轴方向。在给连续体机器人两端施加一定的边界支撑作用下，当图4中的两段式左半段的磁极性沿着x轴负方向且右半段的磁极性沿着x轴正方向时，左边的磁偶极子在B的作用下沿顺时针方向偏转一定角度而右边的磁偶极子相应地沿逆时针方向偏转一定角度后，将呈现出U型变形形态。依此类推，另外2种变形形态对应的2个四段式磁响应软连续体机器人的分段磁化模式设计如图4所示。

图4 连续体机器人的分段磁化模式设计示意图

3 磁响应软连续体机器人的仿真

3.1 磁性颗粒含量对变形的影响

针对上述几种预定义形态下的分段式磁响应软连续体机器人，本文基于ABAQUS的二次开发功能进行了有限元仿真分析。首先验证了设计的3种分段式磁响应软连续体机器人在匀强磁场空间中确实达到了预定义的二维轮廓，所展示的仿真结果如图5所示。

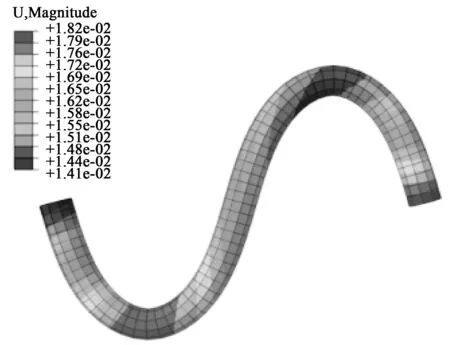
b)弦线型

c)W型

有关连续体机器人的结构参数和物理参数以及驱动磁场的信息见表1。本文主要关心的参数是CR的直径和长度以及硬磁软材料中磁性颗粒的含量。

表1 连续体机器人的参数

由硬磁软材料制成的磁响应软连续体机器人的磁性和力学性能随着磁性颗粒含量的变化而变化，本文在初始仿真验证中规定了磁性颗粒的体积分数为20%。为进一步研究磁性颗粒含量与连续体机器人驱动性能的关系，分别仿真模拟了在NdFeB体积分数为10%、15%、20%、25%以及30%的情况下几种磁响应软连续体机器人的变形结果。通过提取每个变形形态下所有仿真结果的轮廓曲线并将它们放置在一个坐标图中以便对比。图6所示为U型对应的两段式磁响应软连续体机器人在沿y轴正方向的匀强磁场下的变形情况，图7和图8分别展示了弦线型和W型对应的四段式磁响应软连续体机器人的变形轮廓。总的来看，在驱动磁场固定的情况下，磁性颗粒含量的不同导致分段式磁响应软连续体机器人的变形程度有所不同。通过横向和纵向对比3组变形轮廓可以进一步得出：不管连续体机器人的分段数和磁化模式如何，它们均在磁性颗粒含量为20%时表现出最明显的变形。

图6 不同NdFeB含量下U型连续体机器人的变形轮廓

以连续体机器人变形形态的周期宽度作为评价指标，宽度越小则变形程度越大，表2显示了具体的数据结果。

图7 不同NdFeB含量下弦线型连续体机器人的变形轮廓

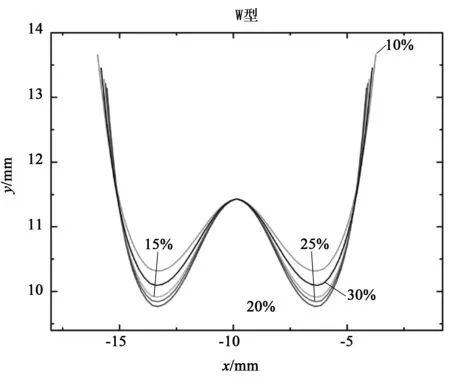
图8 不同NdFeB含量下W型连续体机器人的变形轮廓

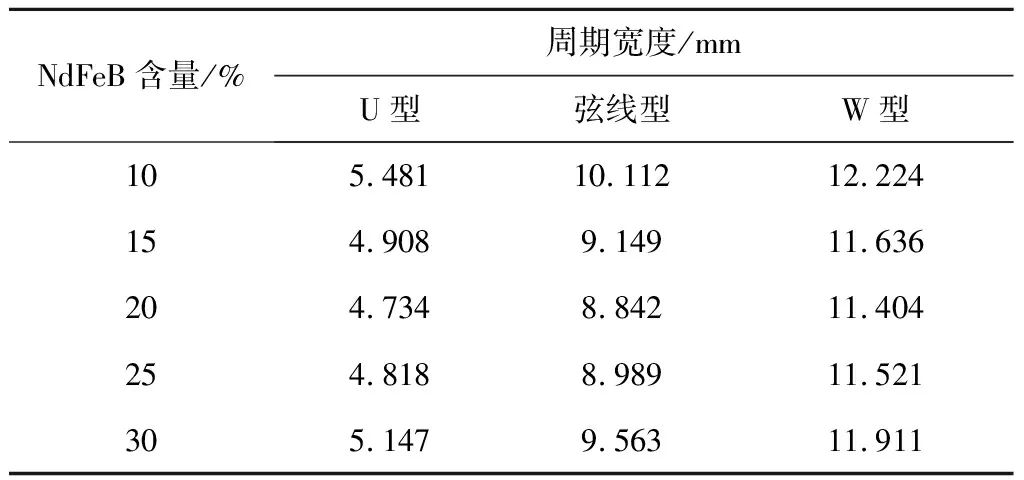
表2 不同NdFeB含量下变形形态的周期宽度

基于磁性颗粒含量对分段式磁响应软连续体机器人的变形影响分析，可以认为在不考虑其他影响参数的情况下，磁性颗粒体积分数为20%时连续体机器人的驱动性能最强。这意味着可以对用于特定任务的分段式磁响应软连续体机器人的驱动性能进行磁性颗粒含量这一角度的优化设计。

3.2 长径比对变形的影响

从单段的磁响应软连续体机器人的变形解析式可知，挠度与结构参数，即长径比，存在二次方的非线性关系。本文进一步研究了分段式磁响应软连续体机器人的变形与长径比的关系。假设驱动磁场固定不变且磁性颗粒的体积分数为最佳驱动设计下的20%，对长径比分别为10∶1、16∶1、20∶1、25∶1(长度固定为16 mm)这几种情况下的分段式磁响应连续体机器人进行仿真模拟。同样地，从仿真结果中提取每种变形形态对应的曲线轮廓，图9～图11所示分别展示了U型、弦线型和W型对应的分段式磁响应软连续体机器人的变形轮廓。通过横向和纵向对比可以得出：不管连续体机器人的分段数和磁化模式如何，它们的变形程度均随着长径比的增大而增大。从变形形态的周期宽度变化可以看出，长径比对变形程度的影响比磁性颗粒含量更明显。对于两者的数值关系，可以通过模拟更多组长径比下连续体机器人的变形并对提取的仿真结果进行曲线拟合得到，本文中不做深入探究。

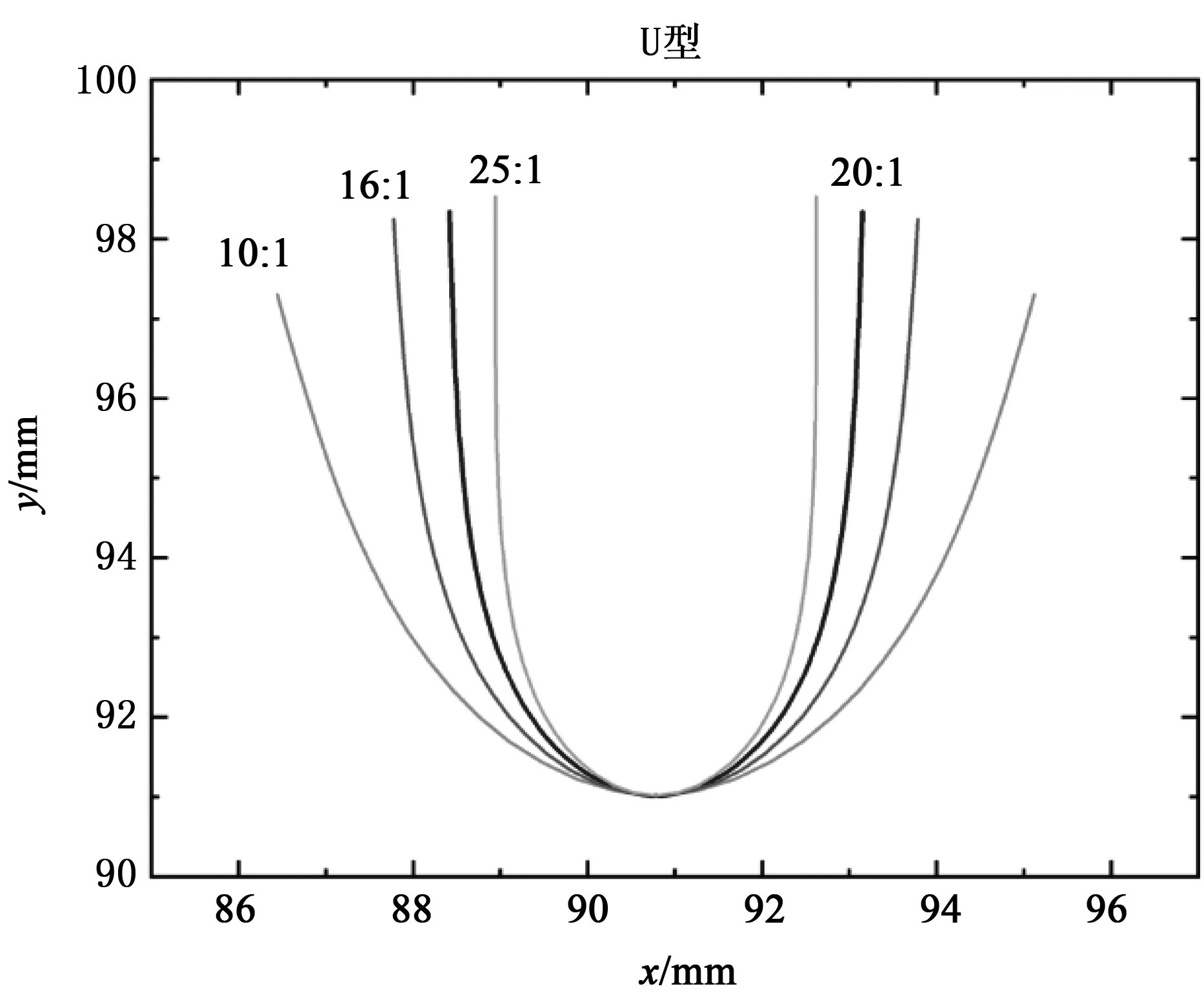
图9 不同长径比下U型连续体机器人的变形轮廓

图10 不同长径比下弦线型连续体机器人的变形轮廓

图11 不同长径比下W型连续体机器人的变形轮廓

4 结语

通过上述研究可以得出如下结论。

1)以用于介入式治疗的亚毫米级铁磁软连续体机器人为原型，提出了一种新颖的分段式磁响应软连续体机器人的概念。通过将连续体机器人分为若干段并设计每一段的磁化模式，就可以驱使它们在一定磁场下达到预定义变形轮廓。本文根据磁性颗粒在磁场下的变形规律展示了对几种变形轮廓的分段及磁化模式的设计方法。

2)根据硬磁软材料力学模型以及其有限元分析的用户单元子程序UEL，开发了基于ABAQUS二次开发功能的分段式磁响应软连续体机器人的有限元仿真方法。验证了几种分段式磁响应软连续体机器人均能够实现预定义变形轮廓，有效说明了该设计方法的正确性。

3)在此基础上，分别研究了磁性颗粒含量和长径比对分段式磁响应软连续体机器人变形的影响。通过分析多组仿真结果得出最佳驱动性能下连续体机器人的材料参数及结构尺寸设计。