热-氧-辐照复合环境下硅泡沫加速老化研究进展
岳动华 靳 凡 韦利明 王罗斌
(中国工程物理研究院总体工程研究所 绵阳 621999)
20 世纪50 年代美国道康宁公司首先研制出有机硅泡沫塑料[1-2]。在聚合物材料中,有机硅材料是以Si-O-Si 键交替组成其主链、以有机基团为侧链的半无机高分子聚合物。这使得硅橡胶具有耐热、耐寒、耐化学品等较好的耐久性,另外,微开孔型硅泡沫还具有重量轻、隔热缓冲、高可压缩性等优点。与普通有机高聚物材料相比,硅泡沫可在-50~170 ℃温度范围内保持弹性,广泛应用于航空航天、汽车发动机密封、户外零部件、隔热阻燃、电子设备甚至生物医疗等领域。例如,美国LLNL国家实验室生产的M97*、M9763等系列硅泡沫,已在某些特殊装置系统中用作压力垫。这些支撑泡沫的作用是在相邻组件之间分配应力,维持各种组件的相对位置,并减轻由于制造公差和温度变化引起的组件尺寸失配的影响。然而,在使用中,这些硅泡沫会长时间承受连续的压缩应变、温度、辐照等应力,材料不可避免地出现老化、劣化现象,如图1 所示。材料老化使得硅泡沫压缩永久变形、载荷保持率及应力应变响应发生永久变化[3],从而导致减震缓冲性能下降,支撑可靠性降低,甚至导致系统失效。
对聚合物在热-氧-辐照复合环境下的材料性能和老化行为进行预测以及准确理解一直是装备寿命研究的重点。美国国家实验室基于《库存管理与维护计划》中的增强监测项目对硅泡沫的热氧老化、辐照老化规律和退化机理进行了长时间研究,并取得了大量的研究成果[4-5]。为更逼近装置库存中的真实应力环境,其研究范围涵盖了热氧加速老化、辐照单因素老化、多应力作用下的自然老化等,研究成果对进一步探究硅泡沫老化机理、准确评估装备寿命、以及提高装备可靠性等起到了重要支撑作用。因此,硅泡沫多因子加速老化规律和退化机理研究具有重要的工程价值。
已有研究表明,热-氧-辐照组合条件下的老化不仅仅是传统的光热暴露问题(自然老化问题),而且还存在纯热驱动或辐照主导相互竞争的退化过程。这意味着加速老化实验并不能像传统的热老化研究那样通过简单升高温度来进行加速[6-8],还须考虑辐射效应[7,9]。此外,在进行加速老化实验时,还应该考虑聚合物加速氧化的局限性,比如扩散极限氧化(DLO)效应,这一效应将使得加速试验数据变得复杂且难以解释。此外由于直接测试退化速率非常困难,通常的办法是利用材料机械性能的变化,例如拉伸伸长率[7,9-10]等进行衡量。在中低剂量率(100 Gy/h)下温度是聚合物退化的主要驱动力,加速退化速率的方法较为简单,即确定参考温度、数据平移叠加、确定热活化能Ea。而在高剂量率下,热降解和辐射损伤将同时存在,还可能发生额外的协同作用。早期有学者提出,辐射主要是通过自由基引发反应,随后的氢释放和主链断裂或交联是由剂量率来驱动的[11-12]。但是材料的氧化还涉及二次化学反应,包括后续的氢过氧化物分解、自由基转移反应、断裂碎片的逸出以及更复杂的聚合物断裂/交联化学反应,这都将引起材料性能的改变,通常会进一步导致伸长率下降。这意味着在高温高剂量率下,除了简单的辐射引发氢过氧化物形成以外,氧化退化还涉及到后续的反应步骤,交联和断裂通常会同时发生,其比例取决于材料、热氧条件和剂量率。对于交联型的聚烯烃材料来讲,氧化断裂是其主要的降解途径,导致其弹性降低[10,13],在惰性气氛保护下交联反应则占据主导。对于非饱和的弹性体材料往往在氧化条件下发生交联,从而导致模量增加和硬化[14-16]。同时由于潜在的DLO 效应[17]以及更具竞争性的快速烷基自由基重组[18-19],通常会随着剂量率的增加引起额外的交联反应,模量硬化行为已由磨损和纳米压痕实验结果给出[20-22]。有大量的证据表明,虽然辐射主导的老化具有接近于零或较低的活化能[9,23-24],但没有先验的证据表明辐射主导的氧化降解不具有温度依赖性。简而言之,辐照与温度之间的协同效应将共同决定材料的活化能。如何进行合理的老化加速、取得有预测价值的实验数据、建立有效的综合老化反馈模型等,这些都是我们当前面临的重要挑战。
本文针对硅泡沫的多因子加速老化这一问题,主要从实验和理论两方面展开论述。在充分调研国内外硅泡沫热氧老化、辐照老化以及组合条件老化研究现状的基础上,对单因子和多因子加速老化的寿命理论模型进行了梳理,对不同模型的发展演变过程以及各自的适用范围进行了讨论;其次介绍了不同的预测模型在硅泡沫多因子加速老化实验研究中的应用情况,总结了当前常用的多因子加速老化实验方法及最新进展;最后对目前硅泡沫多因子加速老化的理论方法和实验手段中存在的问题以及未来的发展趋势进行了展望。
1 硅泡沫热氧老化研究
导致聚合物分子量降低的三个基本机制是已知的:解聚、降解和破坏[25-27]。解聚反应包括聚合物热分解为单体;降解过程是聚合物的部分分解,分解成比原始聚合物小但分子量较大的碎片[28];破坏过程代表聚合物的进一步分解,同时分离为除单体以外的低分子量化合物[26]。退化也可以是结构变化的过程,这种变化可能是由硅泡沫材料在长期外部因素(例如物理的热、紫外线辐射、光辐射、高能量辐射、机械应力等;化学的臭氧、氧气、化学物质、水蒸气等)导致的结构性能下降。此外,在实际服役过程中还有许多其他复杂的因素导致材料退化。在常规条件下,影响弹性体退化的所有因素中臭氧、氧气和高温是最重要的,这通常被称为热氧老化[29]。当然光和其他辐照同样会导致材料降解,我们将在第二节讨论这一问题。
仅在热氧老化过程中,老化速率还取决于作用的持续时间、杂质类型和含量、试样的厚度和形状等[30]。迄今为止,对聚合物和塑料降解过程进行的研究表明,聚合物的敏感性很大程度上取决于结晶度,结晶聚合物比无定形聚合物更有抵抗力。此外研究发现,具有线性结构的聚合物比支链的聚合物降解更快[31]。聚合物的分解还取决于其分子量,分子量越大分解越慢[32]。加快降解过程的另外一个重要因素是特定的化学基团,例如酰胺、酯和脲基团可加速聚合物的降解,因为它们易于水解[33]。每种类型的聚合物降解都有其特定的分子机理,此处我们不对其化学反应动力学过程进行赘述。
1.1 热氧加速老化实验
通常材料的老化需要数年甚至数十年才能看到性能变化,加速老化测试是为了模拟自然条件在实验室中进行的试验,其中人为使用和增强了影响聚合物加速退化过程的各种因素,以达到加速老化节省时间成本的目的[34]。在实验室条件下的加速老化测试技术的应用大大简化了实验过程及其分析,基于此,可以得到材料的耐老化特性定性或定量的评估。
为研究聚合物的热氧加速老化,应确定产品的工作条件,加速老化测试是在比潜在的工作条件下更苛刻的环境下进行的,加速老化过程应选择几个升高的温度值(或提升氧气浓度),化学反应的速率随温度或氧气浓度增加而加快。对聚合物样品进行高温处理可以确定温度与降解反应速率之间的关系。通过外推,可以估算出特定温度下材料在一定时间后的降解程度,反之,也可以推算达到一定的降解程度所需要的时间[7]。也可以选择材料特定的机械性能,例如拉伸伸长率、应力松弛率等来表示材料的退化程度。
早在2005 年,张凯等[35-36]对硅泡沫材料进行了加速老化研究,得到了硅泡沫在老化过程中性能变化指标P和老化时间t的指数关系:在125 ℃以下,老化速度常数K与温度T的关系符合阿伦尼乌斯方程,进而对硅泡沫压缩永久变形进行了预测。2009年,颜熹琳等[37]对45%压缩应变状态下的硅泡沫进行了加速老化实验研究,发现压缩永久变形随老化时间和温度的增加而增大。美国桑迪亚国家实验室White 等[38-39]对硅橡胶O 型密封圈进行了长达10 年的老化实验研究,发现硅橡胶密封圈的拉伸伸长率退化随着温度的增加而加剧,并且退化率与温度符合阿伦尼乌斯方程,加速因子与时间的导数为线性关系。Celina 等[40]利用充有高浓度氧气的温控箱等实验条件,研究了在热氧条件下硅橡胶的加速老化问题,对比了硅橡胶拉伸伸长率、断裂强度、氧气消耗量与温度的关系,发现在利用阿伦尼乌斯方程拟合高温加速老化实验数据获取反应活化能时应注意DLO 效应的影响,并且发现DLO 效应使得试样表面硬度远大于内部硬度,说明试样表面与内部氧化程度不均,进而影响试样的拉伸断裂强度。实验还发现,DLO效应对老化后的硅橡胶拉伸断裂伸长率的影响并不明显。
1.2 Arrhenius模型
1930 年,Montsinger[41]首次提出了绝缘寿命与运行温度之间的关系,即温度每升高8~10 ℃,绝缘材料的使用寿命就会减少一半。美国学者Dakin[42-43]将老化解释为材料的氧化裂解,认为温度影响热老化过程的化学反应速率,进而影响绝缘材料的寿命,从动力学角度上解释了绝缘寿命与温度的关系,并建立起了热老化过程与化学反应速率理论,即著名的Arrhenius 方程之间的关系。基于Dakin 理论结合Arrhenius 方程得出的热老化单因子的动力学寿命模型如式(1)所示。

式中:LT表示绝缘材料热老化寿命;T表示绝对温度;k表示Boltzmann 常数,k=1.380 649×10-23J/K;AT表示频率因子,是与温度无关的常数,取决于绝缘材料的寿命终止判据以及老化过程的化学反应速率常数;G表示相应的活化能,kJ/mol。对于具体的聚合物绝缘材料,AT和G一般由实验得出。
由式(1)可以看出,log(LT)与1/T呈线性关系,这一规律常被用来验证实验结果和理论模型的一致性。Arrhenius方法假定高温下的降解机理和常温下相同,但由于不同绝缘材料老化过程的复杂性,部分实验结果并不满足这一线性关系。如果降解机理随温度发生变化,则使用Arrhenius方法进行的预测可能会出现较大误差。为了克服这一困难,Eyring等[44]在修正的Arrhenius 方程基础上提出了修正的热老化寿命模型,从材料的自由能、熵和焓出发,基于化学反应的统计理论,推导了更为严格的反应速率公式,认为频率因子AT是绝对温度T的函数,即AT=A0Tm或A=A0(T/T0)m,其中,m为无量纲常数,Arrhenius 方程可看作为Eyring 方程的一种特殊形式。
1.3 时间-温度叠加模型
时间-温度叠加原理(TTSP)是硅泡沫加速试验的另一种较为准确方法,该方法与阿伦尼乌斯方法一样,通过经验假设温度和时间对材料特性的影响是等效的,即认为对于在较高温度下的短时加速老化,材料性能的变化与室温长时作用下测得的变化相同。与阿伦尼乌斯方法不同的是,TTSP由确定的AT因子组成,其材料性能与温度T或时间t的关系满足公式(2)。

式中:AT表示位移因子;T是绝对温度;T0是最小温度(通常是时效温度的最小值)。对于实际应用过程中可以选定温度函数,以使所选响应函数的各个等温线段沿对数时间刻度移动,并创建一条T0主曲线。与阿伦尼乌斯方法一致,通过经验上拟合的偏移系数相对于绝对温度值的对数图中创建一条直线,即可以为每个所需温度计算偏移系数。一旦确定了位移系数,就可以推断所有温度下的变化行为。与阿伦尼乌斯方法不同的是,TTSP方法对所有老化温度值都使用所有温度点数据进行拟合。材料在工作温度下的寿命te可以通过位移因子log(ATe)来确定,其与参考温度点的寿命t0满足公式(3)。

Yin 等[45]利用TTSP 方法对PPMA 在不同老化温度下的拉伸强度进行了研究,发现在30~50 ℃范围内位移因子ATe与温度的倒数呈线性关系,而55 ℃下的结果与直线有很大偏差。因此,需要强调的是TTSP 方法仅在恒定加速度的假设下有效。在其他情况下,可能由于反应速率甚至老化机理的改变而出现测量误差,导致寿命预测值偏离直线。
1.4 Wiliams-Landel-Ferry(WLF)模型
WLF 方法可用于根据任何物理性质预测聚合物材料的寿命[46]。在给定材料特性对时间具有复杂依赖性或降解过程受到扩散限制的情况下,例如考虑DLO 效应,使用WLF 方法可以获得较好的预测结果[47]。与Arrhenius 方法相比,该方法可以更好地预测聚合物玻璃化温度(Tg)以上的材料行为。WLF模型本质上是使用时间-温度叠加,没有任何其他假设,即排除了任何温度下材料特性对时间的依赖性。WLF方法中AT因子满足公式(4)。

式中:AT是变量移动因子;C1和C2是实验拟合常数,取决于温度和所测试的材料;T0是参考温度(Tg≤T0≤Tg+100 ℃)。当给定属性在不同温度下对时间的依赖相似时,可以使用WLF 方法进行处理。对应于不同温度值的曲线彼此平行移动了偏移因子AT。通过对比公式(2)、(3)可知,当C1和C2满足公式(5)时,WLF模型可退化为TTSP模型。

WLF 方法通常和Arrhenius 方法相结合,用于研究不同温度和频率下聚合物材料的流变行为。利用WLF与TTSP方法相结合更加适用于聚合物的动态力学性能和粘弹性研究[48]。采用带有WLF方程的TTSP 方法成功拟合了一系列木塑复合材料的短期蠕变测试结果,发现木塑复合材料是一种简单的热流变材料,其时间-温度叠加仅需要水平移动。
1.5 反幂指数模型
反幂指数模型通常用于金属疲劳寿命预测、电容器介电失效以及多组件系统老化失效寿命预测等。其满足公式(6)。

式中:L为失效时间;k,n为与材料和测试方法相关的拟合参数;V为环境应力,如温度、浓度、电压、电流等。该模型很少用于硅泡沫热氧老化寿命预测,在材料疲劳损伤预测中较为常见[49]。
从热氧老化本质来讲,热氧老化材料在热氧环境下发生化学反应,其反应速率与不同温度下氧分子热振动与材料表面碰撞的概率密切相关,温度越高,空气中氧分子的运动速度越大,与材料表面的碰撞概率越大,反应速率越快,反之亦然。与以上所有的老化模型中,Arrhenius 模型是应用范围最广、且最便于应用的模型,其有效性在多种材料的热氧加速老化预测中已得到证明[49]。应用Arrhenius方法的关键是通过加速试验数据拟合得到材料老化反应的活化能。然而,通过较窄的温度区间和老化时间数据来拟合获得活化能,进而预测材料寿命是非常冒险的,这就要求当且仅当在实验温度范围内,敏感参量(拉伸断裂伸长率)与氧化百分比呈线性关系时,Arrhenius 方程才能严格成立。Eyring 模型是唯一的一个基于物理原理可以考虑温度、时间、反应速率协同作用的模型,虽然该模型较为精确,但由于仅有少数材料可直接获得该模型的部分参数,在实际应用中很难获得普适的经验参数。时间-温度叠加模型并没有突破Arrhenius 公式的经验假定,其优点在于可以利用所有的实验数据进行拟合,并且用于特定温度寿命的预测。WLF 模型通常用于聚合物玻璃转化点以上的温度区间,可预测材料的流变及粘弹性行为。
2 硅泡沫辐照老化研究
相比于热氧老化,硅泡沫辐照老化开展的时间相对较晚。辐照研究主要集中在以辐照损伤机理和材料性能变化的定性描述上。研究人员始终对剂量率效应、粒子源替换等效性等方面存在较大争议,因此除累积损伤模型外,辐照加速老化方面缺乏物理意义明确的数学模型。1957年,Robert对γ辐照条件下硅橡胶材料的老化行为进行了研究[50]。对硅橡胶的耐辐照能力进行了对比和评价,分别测定了硅橡胶耐辐照的剂量范围。近年来针对辐照场中使用的硅橡胶进行的研究主要集中在辐照源、剂量率、总剂量、气氛等对硅橡胶性能的影响。揭示了不同粒子源轰击下硅橡胶的氧化行为,重粒子辐照主要以粒子注入为主,低线能密度辐照主要以电离为主,主要表现为辐照产生的自由基差异[51]。鉴于聚合物材料辐照损伤的复杂性,我们分为以下几个方面进行讨论。
辐照引起力学性能变化,硅橡胶在高能辐射下会同时发生辐射交联和裂解[52]。胡文军等[53]进行了硅橡胶中子辐照效应研究,发现硅泡沫经辐照后发生了二次交联,使得硅泡沫表观密度、拉伸强度和拉伸伸长率增加。黄玮等[54-55]采用60Co γ射线对不同气氛下的甲基乙烯基硅泡沫进行了研究,分析了辐照后样品的气体产物及微观结构与力学性能间的关系。实验发现,辐射反应气体主要以低分子量的CH4、H2和支链破片为主,在剂量小于2×105Gy 时,样品以辐射交联为主,超过该值后以降解为主[56]。Labourau 等[57]对惰性气氛下SX358 硅泡沫辐照力学行为进行了研究,实验发现,辐照导致硅泡沫交联密度增加,压缩性能增强,并且发现硅泡沫微观泡孔结构并未发生明显改变,这与黄玮等人在空气中的实验结果有些许差异。Wang[58]、晏顺坪[59]等实验发现,辐照后硅泡沫压缩模量可显著增加,并且保持超弹性特征,基于此建立了不同剂量下的修正Hyperfoam 本构模型,获得了0~1 MGy 剂量范围内硅泡沫的压缩力学行为。史平安[60]、王浦澄[61]、陈洪兵[62]等对预压下的硅泡沫进行了辐照老化研究,同样发现辐照后材料变脆,延伸率下降;剂量超过500 kGy时,泡孔发生明显的永久变形,认为低剂量下交联效应占优,而高剂量下损伤降解效应占据主要作用。对照组、50 kGy-80 ℃、500 kGy-80 ℃三组预压硅泡沫辐照前后扫描电子显微镜照片如图2所示[62],图2中第一和第二列为表面形貌,第三和第四列为侧面形貌。

图2 预压硅泡沫辐照前后扫描电子显微镜照片Fig.2 SEM micrographs of irradiated silicone foams under pressure
气氛对硅橡胶辐照行为也有重要影响。不同气氛中γ 辐照的热稳定性表现差异较大,真空和惰性气氛中硅泡沫的热稳定性更高,而空气中热稳定性较差,这是由于空气中的氧气参与了反应[63]。黄玮等[64]对比了甲基乙烯基硅泡沫与甲基苯基乙烯基硅泡沫的耐电子束辐照特性,发现两者经辐照后都有气体小分子产生,且甲基乙烯基硅泡沫的产量更多,其压缩机械稳定性较差,但应力松弛率较好,上述实验结果表明具有π键的苯环对辐射具有良好的保护作用[65]。
Gillen等[66]发现,对于不同的材料,吸收剂量和剂量率的影响具有较大差异。对于硅橡胶而言,机械性能的下降仅与总剂量相关,受剂量率的影响并不明显。而对于交联的聚烯烃等材料受剂量率的影响显著。刘波等[51]发现,在相同吸收剂量下,随剂量率的下降交联密度增加,拉伸伸长率、辐射降解分子量下降,并提示采用升高剂量率进行硅泡沫加速老化的风险。郝晓飞等[67]发现,在惰性气氛保护下,γ射线辐照硅泡沫时,Si-CH3结构单元最易受到γ 射线的影响。在低吸收剂量下,Si-CH3相对含量随着吸收剂量的增加而减小,在高吸收剂量下,近表面C元素的含量明显升高[61]。总体而言,硅橡胶的辐照老化受多种因素的影响,老化行为较为复杂。陈洪兵等[68]就当前硅橡胶辐射老化的研究进行详细综述,总结了吸收剂量、剂量率、环境因素以及添加剂对辐射老化的影响,对常用的辐射老化表征方法(色谱、质谱、核磁共振、常规力学性能表征等技术方法)进行了概述,遗憾的是其并未对适用于低剂量率超敏感氧气消耗量(UOC)这一老化表征方法进行阐述。另外值得注意的是,近年来随着物理、化学和材料等多学科交叉的不断深入,基于凝聚态物理密度泛函理论,及其相关的量子化学仿真、反应分子动力学计算方法等发展十分迅速。刘波等[55,69-70]、Kroonblawd 等[71]在揭示硅泡沫材料辐射机制、热力学和化学反应动力学等方面做出了一系列开创性工作,系统研究了硅泡沫在辐照-温度作用下降解、交联、释气行为,并给出了化学动力学过程,为后续硅泡沫材料宏观物理特性及工程兼容性研究奠定了基础。
3 热-氧-辐照环境下加速老化研究进展
硅泡沫在核电站或相关应用中将不可避免地面临热-辐射环境,对于长时热辐射环境下的材料预测一直是加速老化研究的重点。与传统的单一因素热降解或辐照老化研究相比,在热氧-辐射复合条件下的聚合物老化本质上更加复杂。无论基于何种假设的加速老化方法都必须同时包括热降解途径和辐射降解途径。由于升温导致的是分子振动频率增加和气体分子运动加快,其能量范围在keV量级,温度上升促进的是化学反应速率的增大;而γ 射线的能量范围在MeV 量级,化学键发生的是电离损伤,剂量率增加辐射电离损伤增大;若不考虑辐射降解产物参与二次化学反应,可将这两种途径视为独立的并行过程。这意味着增加剂量率不再有助于氧化驱动的降解,仅仅是等比例增加辐射损伤程度。虽然有大量研究表明,辐射主导的降解具有接近于零或较低的活化能,但没有先验的证据表明辐射主导的氧化降解不应具有有限的温度依赖性[9,23-24]。实际上,在一些较早的关于PVC或PE的研究中[72-74]得出的结论是温度在较高的剂量率下仍然起作用,因为它影响过氧化氢驱动的后续化学反应。为了确定适当的老化模型,可以考虑通过两种活化能(温度活化能和辐照等效损伤活化能)的组合来更好地描述材料的组合退化过程。
3.1 Gillen和Clough模型
伊藤等[75-77]首先提出了辐射项的单独活化能概念,并给出大致的估算(9~12 kJ/mol),同时指出剂量率指数是附加协同效应的贡献。由于热活化能在百kJ/mol 量级,远大于辐射活化能,早期的研究中将材料老化表示为热和辐射贡献之和,来自辐照加速老化的数据以等效损伤(DED)或降解速率的剂量来表示,将其直接叠加到热加速老化方程。
在给出加速老化损伤模型之前,我们做出以下几个定义,定义适用于后续加速老化数据解释和加速老化模型。我们知道的是在空气中老化条件下,聚合物将发生氧化,导致材料性能发生变化,例如拉伸伸长率降低,随着时间的流逝材料性能的损失称之为退化,退化速率取决于特定的老化条件,它可以在服役环境条件和加速条件之间变化(高温、高剂量率),老化条件由温度和剂量率给定。在Gillen 的文献和报告中[9,23-24],对于其研究的大多数聚合物而言,氧化水平决定了拉伸伸长率,总体退化状态或损伤水平C=tr,其中t是老化时间,r是退化速率。材料达到等于损伤水平C的氧化量所需的时间成为等效损伤时间(TED),由t=C/r给出。对于任何损伤水平C也可以定义等效损伤的剂量(DED单位Gy)通常由DED=TED×γ给出,其中γ是辐射剂量率(Gy/h)。若假设退化期间的剂量率恒定,升温加速老化的退化速率通常由位移因子AT来描述。当剂量率为零时,这一问题即简化为单一因素热氧老化,退化率r(T)仅为温度T的函数且与位移因子AT成正比,由位移因子和温度倒数的实验数据提取热活化能Ea。基于辐照等效损伤假设,Gillen 和Clough[23]给出的简单辐射热降解模型如公式(7)所示。

式中:Ea是热速率活化能;R是玻尔兹曼常数;γ为剂量率,f(γ)为辐照项,当剂量率为零时辐射项为零,辐射降解率最简单的函数形式为f(γ) =kγ,辐照项与剂量率成线性正比关系,将该表达式代入DED中可得式(8)。

3.2 Burnay模型
1990 年,Burnay[78]在前人工作的基础上,建立了一个更广泛的热和辐射老化综合经验模型,作为对温度和剂量率相关的偏移因子的一种方法,其在很多材料的复合环境老化中获得成功,该模型由公式(9)给出。
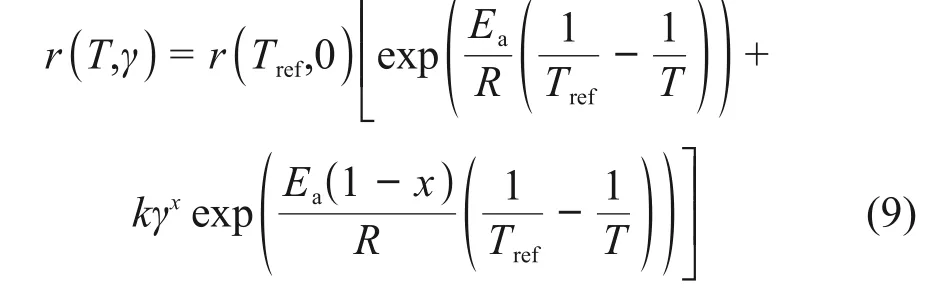
基于Burnay 工作的更广泛的热-辐射退化模型,其有效退化率是温度和剂量率两个独立的并行过程之和。热项和辐射项均有各自Ea,且具有独立的温度依赖性。然而对于大多数弹性体来讲,辐射分量的Ea通常较低,即x接近1。因此该模型可以简化为Gillen和Clough模型。同时根据公式(9)可给出辐照等效损伤剂量DED,如公式(10)所示。

与第一种模型不同的是,Burnay模型分两步拟合温度剂量率数据,活化能参数Ea仅有热数据确定。由所有在参考温度Tref下获取的不同剂量率的数据都用于拟合参数k和x的值。值得注意的是,这两个分析步骤是独立的,这也就意味着Burnay模型隐藏着热和辐射对总氧化/退化率的贡献之间没有协同作用的假定。但可以通过增加的辐射活化能这一参数适应随剂量率增加的协同作用。同时当参数x小于1时,表示随着剂量率的增加,某些材料的辐射等效氧化效率降低,从而对高剂量率下的材料行为的描述进行微调。对于参考温度下不同剂量率DED代表所选的特定等剂量,通过剂量率和总剂量双对数曲线在不同温度数据集的平移,可以得到不同DED水平的辐照损伤加速因子,进而拟合出具有近似为辐射活化能的值。但由于次级辐射项的贡献无法精确描述,通过引入额外自由度的Burnay模型是描述较高剂量率老化行为的首次尝试。利用Gillen模型和Burnay模型分别生成Arrhenius图(图3)[79]。

图3 Gillen模型(a)和Burnay模型(b)生成的Arrhenius图Fig.3 Arrhenius plotsgenerated by Gillen model(a)and Burnay model(b)
从图3可看出,对于参考温度Tref=28 ℃、热活化能为80 kJ/mol、x≤0.9 时,我们注意到两种模型在低剂量率下,Arrhenius 曲线几乎是线性的。可以利用低剂量率曲线拟合以确定适当的热活化能Ea。在高剂量率下,即由辐照主导的老化模式下,Gillen模型的辐照活化能接近于0,Burnay 模型在高剂量率下的等效辐射活化能约为8 kJ/mol,可以较好地描述高剂量率下热-辐照耦合效应。然而,Burnay 模型本身也有其局限性,例如实际实验数据的退化速率、DED和移位因子可能无法满足简单的叠加关系,这意味着不能利用全局的实验数据集对材料老化行为进行预测,这就导致不同的数据子集拟合得到的Ea存在差别,如何确定恰当的Ea以更科学地预测材料老化行为将变得非常困难。
3.3 修正的热-辐射退化模型
在Burnay模型的基础上,将热活化能和辐照等效活化能解耦,在辐射剂量项中添加独立的Ea拟合值,以获得更大的自由度,那么,可以在拟合高剂量率实验数据中具有更强的影响。经验热-辐射退化模型以及该模型对应的辐射等效剂量DED 如公式(11)、(12)所示。
同样为了赋予辐射项更大的自由度,不必受到DED 模型曲线完美叠加的限制,Celina 等[79]对经验热-辐射退化模型做了进一步修正,添加可Burnay模型中经验可调参数x。其表达式如公式(13)、(14)所示。

在经验热-辐射退化模型以及修正的经验热-辐射退化模型拟合实验数据时,其放宽了对高剂量率曲线收敛的限制。这两种经验的热-辐射退化模型与Burnay模型最大的区别是,由于其具有相同的辐射活化能E2,在高剂量率下产生平行的DED 水平,而Burnay 模型在高剂量率下迫使DED 对剂量率的斜率等于(1-x)。必须给予说明的是,为了使DED曲线完全重叠,在任何可能的等剂量条件下的Arrhenius曲线都应表现出单一的斜率,即热活化能Ea的特性。此外Burnay模型不允许辐射Ea项和剂量率的比值独立变化,而修正热-辐射退化模型可弥补这一缺点。式(11)、(13)两种模型DED 移位因子和温度曲线的对比如图4所示[79]。

图4 公式(11)DED移位因子拟合Ea(a),公式(13)DED移位因子拟合Ea(b)Fig.4 Ea fitted with different shift factors by formula 11(a)and formula 13(b)
从图4 可看出,3 个Arrhenius 曲线在高剂量水平发散,这意味着通常的DED 剂量率叠加不再有效,高剂量率的影响不允许通过简单的数据移位叠加获得。两种模型在低剂量率下的拟合完全一致,而在高剂量率下修正热-辐射退化模型由于增加了一个自由度,可以更好地适配热活化能的变化。值得注意的是,在低剂量率下,Gillen模型低估了辐照等效损伤剂量DED和等效损伤时间TED,而修正模型与Eaton dekoron hypalon 材料的氧化速率数据最为匹配,特别是当剂量率大于1 Gy/h 时,两种模型出现明显差别。
3.4 时间依赖模型和MAC模型
虽然很多材料在热氧老化时会随时间显示具有接近恒定的氧化速率[15-19,80-81],但仍有一些材料(例如PDMI泡沫和尼龙)氧化功率会随时间发生偏移。氧化速率的时间依赖性是一个突出且难以解决的问题。通过在修正的经验模型上添加时间项以外,目前还找不到更好的解决办法,速率时间相关模型如公式(15)所示。

当辐射和温度之间存在相互作用时,氧化/损伤的发展速度快于辐射和温度的相互作用,则协同作用相当于提供了两者简单叠加之外的倍率。伊藤[75-77]过去已经认识到这种协同作用可以提高综合反映速率,并令辐射速率与附加的活化能相关,已达到综合作用的按比例增加效果。

该方法的贡献是定义了一个协同作用的增加比例系数s,如果s=0,那么两者之间无协同作用,如果考虑加速老化,使r(T)增加到x倍,而同时r(R)也增加到x倍,这可能导致综合速率增加到x倍,这种情况下s将保持恒定。然而,当辐射与温度加速条件不匹配时将会引发新的矛盾,即s并不为常数,而是与温度-剂量率相关。假定协同作用的增加比例系数s保持不变,那么可以得到Gillen最新提出的匹配加速条件(MAC)模型[9],即温度加速倍率与辐照加速倍率相等。这也意味着当低温高剂量率时,材料将以辐照老化为主;当处于高温低剂量率时,材料将以温度老化为主,MAC模型如公式(17)所示。

其中:rT+rR为公式(13)所给出的直接叠加模型;f(t)为时间项;f(T,γ)为协同作用交互系数。通过调节f(T,γ)中温度与剂量率相关的比例因子即可对组合条件下材料的老化模式进行拟合。然而,当更复杂的协同作用加速老化行为时,不应期望在多个温度点下实现DED数据的完美叠加。Burnay和伊藤等对辐射项活化能的拟合也起到了和公式(17)相同的效果。
4 结论
本文首先对硅泡沫热氧老化理论模型进行了介绍,对热-氧-辐照复合环境下硅泡沫加速老化领域的研究进展进行了简单回顾。其次,介绍了硅泡沫辐照老化实验以及损伤机理,对硅泡沫在不同剂量率和总剂量条件下的力学响应进行了总结。然后,对多因子加速老化实验方法和最新理论进展进行了介绍。最后,对硅泡沫未来多因子加速老化研究的发展趋势进行了展望。提出面向寿命预测的加速老化模型必须包含热降解和辐照损伤两种机理,而最初的唯象模型将两者作为独立的并行过程,并未考虑协同效应。以后应重点研究热氧、辐照老化不同应力间的协同效应,考虑材料的微观结构和辐照损伤机制,以及由协同作用引起的新的老化机制,将硅泡沫服役老化过程中的宏观性能和微观结构以及热-氧-辐照损伤机制联系起来,这对建立物理意义明确的多因子加速老化及寿命预测模型具有重要意义。
多因子加速老化研究是硅泡沫材料及相关特殊装备的寿命预测的基础。本文通过从单因子热氧老化、辐射老化机理以及多因子加速老化模型三个方面对近年来加速老化研究成果进行了梳理。
(1)单因子老化模式下,基于热氧老化的Arrhenius公式适用于较低剂量率下,以热氧老化为主的场景。基于辐照损伤失效的分析适用于高剂量率、大剂量辐照定性分析。相比于辐照损伤定性分析,目前热氧老化模型较为成熟,与实验数据拟合较为准确,具有很强的预测性。
(2)多因子老化模式下,修正的经验热-辐射老化模型具有较大的使用价值,老化敏感参数主要以氧化率和拉伸断裂伸长率为主,可以将这两种指标纳入寿命模型中。压缩永久变形与应力松弛这两种指标与氧化率之间的关系还需要通过气相色谱或呼吸计的方法进一步研究。
(3)多因子加速老化的实验方法目前尚无统一的标准,在今后的研究中,应采用统一的加速试验方法,根据不同材料和不同性能的考核要求设计相应的加速试验方法并标准化,以提高实验方法的通用性和实验结果的可重复性,交叉对比老化模型对不同材料加速老化数据的适用性。
(4)协同效应在硅泡沫多因子加速老化中的作用尚不明朗,目前相关研究较少。协同效应对材料加速老化的影响机制是未来研究的重点和难点。今后研究中应重点考虑材料的微观结构和辐照损伤机理,以及由协同作用引起的新的老化机制,将硅泡沫服役老化过程中的宏观性能和微观结构以及热-氧-辐照损伤机制联系起来,建立物理意义明确的多因子加速老化模型。
作者贡献说明岳动华完成了文献分析、整理、归纳和综述初稿撰写;靳凡、韦利明、王罗斌三人参与了文献调研和讨论,并对初稿进行修改。全体作者均已阅读并同意最终的文本。

