不定方程x2-72y2=1与y2-Dz2=4的公解

丁 瑜，管训贵

(泰州学院数理学院，225300，江苏，泰州)

1 引言及主要结论

最近几十年，Pell方程

x2-dy2=1 与y2-Dz2=4

(1)

的公解问题一直引起许多学者的兴趣。例如：

(A)d=2,D=2p1…ps(p1,…,ps为不同的奇素数, 1≤s≤6)时，管训贵[1]证明了除开D为2×17，2×3×5×7×11×17以及2×17×113×239×337×577×665 857外，式(1)仅有平凡解z=0。

(B)d=2,D为偶数且D没有适合p≡1(mod8)的素因子p时，乐茂华[2]证明了式(1)仅有平凡解z=0。

(C)d=6,D=p为奇素数时，苏小燕[3]证明了除开D=11时仅有非平凡解z=±6外，式(1)仅有平凡解z=0。

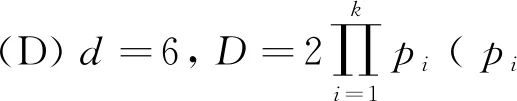
(E)d=6,D=2p1…ps(p1,…,ps是不同的奇素数, 1≤s≤4)时，杜先存等[5]证明了除开D为2×11×97时仅有非平凡解z=±420外，式(1)仅有平凡解z=0。

(F)d=6，D=2n(n为正整数)时，杜先存等[6]证明了除开n=1,3,5分别仅有非平凡解z=±140，z=±70和z=±35外，式(1)仅有平凡解z=0。

(G)d=12,D=p1…ps(p1,…,ps是不同的奇素数, 1≤s≤3)时，过静等[7]证明了除开D为195时仅有非平凡解z=±2外，式(1)仅有平凡解z=0。

(H)d=12，D=2n(n为正整数)时，高丽等[8]证明了式(1)仅有平凡解z=0。

(I)d=30,D=p1…ps(p1,…,ps是不同的奇素数, 1≤s≤3)时，高丽等[9]证明了除开D为483时仅有非平凡解z=±2外，式(1)仅有平凡解z=0。

本文主要讨论d=72，D为偶数的情况，即证明了下列定理。

定理：若p1,…,ps是不同的奇素数，则当D=2p1…ps(1≤s≤4)时，不定方程组

(2)

除开D=2×7×23仅有非平凡解(x,y,z)=(±19 601,±2 310,±68)外，均仅有平凡解(x,y,z)=(±17,±2,0)。

2 关键性引理

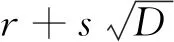
x2-Dy2=1

(3)

的基本解，则有

2)方程(3)的整数解(xn,yn)满足递推关系：

xn+2=2rxn+1-xn，x0=1，x1=r，

yn+2=2ryn+1-yn，y0=0，y1=s；

3)xm+n=xmxn+Dymyn，ym+n=xmyn+xnym；

4)x-n=xn，y-n=-yn。

引理2：Pell方程

x2-72y2=1

(4)

的整数解(xn,yn)具有如下性质。

(iii)xn≡1(mod2)，x2n≡1(mod3)，x2n+1≡2(mod3)，x2n+1≡0(mod17)，x2n≡±1(mod17)，y2n≡0(mod4)，y2n+1≡2(mod4)，y2n+1≡±2(mod17)，y2n≡0(mod17)；

(iv) gcd(xn,yn)=gcd(xn,xn+1)=1，gcd(yn,yn+1)=2，gcd(x2n,y2n+1)=gcd(x2n+2,y2n+1)=1，gcd(x2n+1,y2n)=gcd(x2n+1,y2n+2)=17；

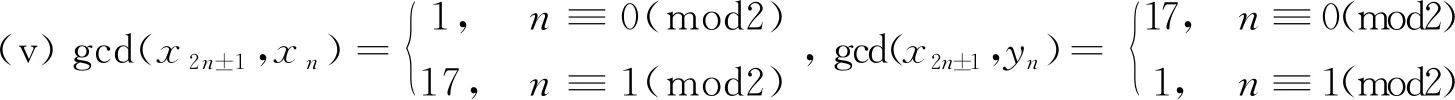
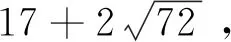
xn+2=34xn+1-xn，x0=1，x1=17

(5)

yn+2=34yn+1-yn，y0=0，y1=2

(6)

并有表1。

表1 Pell方程x2-72y2=1的前7组解

(i)由引理1的3)和4)知，yn+1=2xn+17yn，yn-1=-2xn+17yn，故

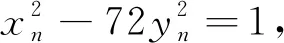
(ii)由引理1的3)可得

(iii)由式(5)知，xn≡1(mod2)。

对式(5)取模3得剩余序列的周期为2：1，2，1，2，…，故得x2n≡1(mod3)，x2n+1≡2(mod3)。

对式(5)取模17得剩余序列的周期为4：1，0，-1，0，…，故得x2n+1≡0(mod17)，x2n≡±1(mod17)。

对式(6)取模4得剩余序列的周期为2：0，2，0，2，…，故得y2n+1≡2(mod4)，y2n≡0(mod4)。

对式(6)取模17得剩余序列的周期为4：0，2，0，-2，…，故得y2n+1≡±2(mod17)，y2n≡0(mod17)。

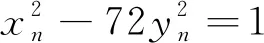
利用引理1的3)和引理2的(iii)可得

gcd(xn,xn+1)=gcd(xn,17xn+144yn)=gcd(xn,144yn)=gcd(xn,144)=1。

gcd(yn,yn+1)=gcd(yn,2xn+17yn)=gcd(yn,2xn)=gcd(yn,2)=2。

gcd(x2n,y2n+1)=gcd(x2n,2x2n+17y2n)=gcd(x2n,17y2n)=gcd(x2n,17)=1。

gcd(x2n+2,y2n+1)=gcd(17x2n+1+144y2n+1,y2n+1)=gcd(17x2n+1,y2n+1)=gcd(17,y2n+1)=1。 gcd(x2n+1,y2n)=gcd(17x2n+144y2n,y2n)=gcd(17x2n,y2n)=gcd(17,y2n)=17。

gcd(x2n+1,y2n+2)=gcd(x2n+1,2x2n+1+17y2n+1)=gcd(x2n+1,17y2n+1)=gcd(x2n+1,17)=17。

(v) 由引理1的3)、4)及引理2的(ii)知

gcd(x2n±1,xn)=gcd(x2nx±1+72y2ny±1,xn)=gcd(17x2n,xn)=gcd(17,xn)。

再由引理2的(iii)知：当n为偶数时，gcd(17,xn)=1；当n为奇数时，gcd(17,xn)=17。

同理可证另两式。证毕、

引理3[11]：设D>0且不是平方数，则丢番图方程

x4-Dy2=1

除开当D=1785，4·1785，16·1785，分别有2组正整数解(x,y)=(13,4)，(239,1352)；(x,y)=(13,2)，(239,676)；(x,y)=(13,1)，(239,338)外，最多只有一组正整数解(x1,y1)，且满足

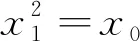
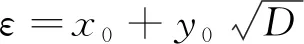
由引理3可得：

引理4：丢番图方程x4-72y2=1仅有整数解(x,y)=(±1,0)。

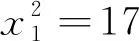
引理5[12]：当a>1,b>0且a是平方数时，丢番图方程ax4-by2=1最多只有一组正整数解。

引理6：丢番图方程289x4-72y2=1仅有整数解(x,y)=(±1,±2)。

证明：因为289为平方数，根据引理5，该方程最多只有一组正整数解，又289×14-72×22=1，所以该方程有且仅有正整数解(x,y)=(±1,±2)。从而该方程仅有整数解(x,y)=(±1,±2)。证毕。

引理7[13]：设D>0且不是平方数，则丢番图方程

x2-Dy4=1

(7)

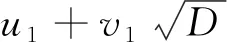
由引理7可得：

引理8：丢番图方程x2-288y4=1仅有整数解(x,y)=(±1,0)和(±17,±1)。

证明：因为288≠1785，288≠28560，Pell方程U2-288V2=1的基本解

且2u1=34不是平方数。根据引理7，方程x2-288y4=1最多只有一组正整数解，而172-288×14=1，故该方程恰有一组正整数解(x,y)=(17,1)。又y=0时，x=±1，因此该方程仅有整数解(x,y)=(±1,0)和(±17,±1)。证毕。

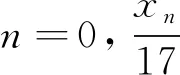
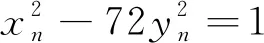
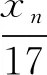
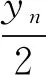
根据引理8可得xn=1或17。由表1知n=0或n=1。证毕。

3 定理的证明

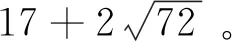
若z=0，可得式(2)的平凡解为(x,y,z)=(±17,±2,0)。

若z≠0，则xy≠0。因此不妨设(xn,yn,z)为式(2)的任一组正整数解，此时

根据引理2的(i)可得

(8)

且n>1。

情形1：n≡0(mod2)。令n=2s(s是正整数)，则式(8)给出

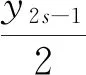
情形2：n≡1(mod4)。令n=4s+1(s是正整数)，根据引理2的(ii)知，式(8)给出

Dz2=y4s·y4s+2=8x2s+1y2s+1x2sxsys

(9)

由引理2的(iv)知，gcd(x2s+1,y2s+1)=gcd(x2s+1,x2s)=gcd(y2s+1,x2s)=gcd(xs,ys)=1，gcd(x2s,xs)=gcd(x2s,ys)=1，gcd(y2s+1,ys)=2。

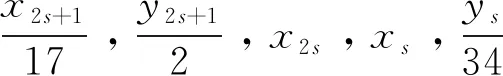
当s=2时，式(9)成为

Dz2=8x5y5x4x2y2

(10)

考虑到2⫮x5x4x2，2‖y5，4‖y2，故式(10)右边给出2的方幂为6，这导致D为奇数与D为偶数的假定矛盾。

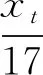
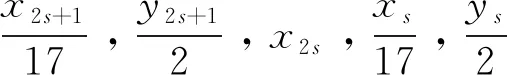
当s=1时，式(9)成为

Dz2=8x3y3x2x1y1=8×19601×2310×577×17×2=2×3×5×7×11×577×1153×682。此时D=2×3×5×7×11×577×1153，即D含有6个不同的奇素因数，与D的假定矛盾。

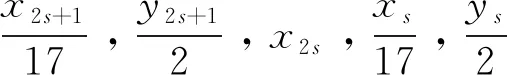
情形3：n≡3(mod4)。令n=4s-1(s是正整数)，根据引理2的(ii)知，式(8)给出

Dz2=y4s-2·y4s=8x2s-1y2s-1x2sxsys

(11)

由引理2的(iv)知，gcd(x2s-1,y2s-1)=gcd(x2s-1,x2s)=gcd(y2s-1,x2s)=gcd(xs,ys)=1，gcd(x2s,xs)=gcd(x2s,ys)=1，gcd(y2s-1,ys)=2。

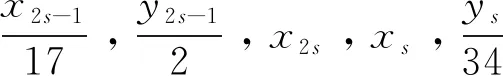
当s=2时，式(11)成为

Dz2=8x3y3x4x2y2

(12)

考虑到2⫮x3x4x2，2‖y3，4‖y2，故式(12)右边给出2的方幂为6，这导致D为奇数与D为偶数的假定矛盾。

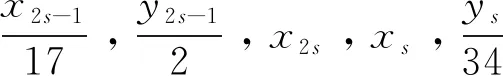
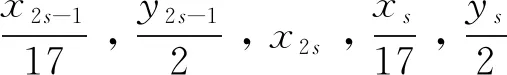
当s=1时，式(11)成为

Dz2=8x1y1x2x1y1=8×17×2×577×17×2=2×577×682。

故有D=2×577，z=68。此时式(2)的正整数解为(x,y,z)=(19601,2310,68)，从而式(2)的非平凡解为(x,y,z)=(±19601,±2310,±68)。

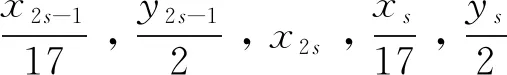
综上，式(2)除开D=2×577仅有非平凡解(x,y,z)=(±19601,±2310,±68)外，均仅有平凡解(x,y,z)=(±17,±2,0)。定理得证。