运用数学步道 发展核心素养
——A4 纸中的数学问题探究
安徽省合肥市第四十五中学橡树湾校区 何 钧 (邮编:230001)
1 问题提出
《义务教育数学课程标准(2011 年版)》[1]提出“数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识、创新意识”是义务教育阶段的十个核心数学能力.《普通高中数学课程标准(2017 年版)》[2]提出高中数学教育的六大核心素养:数学抽象、逻辑推理、直观想象、数学建模、数学运算、数据分析. 将二者对照,会发现二者是一脉相承、螺旋上升的.
本文以《A4 纸中的数学问题》的教学设计和实际教学过程为例,探讨如何运用“数学步道”理念设计教学过程,使得学生的数学核心素养的培养工作在课堂教学中落地,仅供读者参考.
2 教学目标
本节课学生经历观察A4 纸、测量A4 纸、提出猜想,培养学生动手实践、获取信息、数据分析的能力;经历个人思考、小组交流,以及在他人回答问题后的深度思考和问题解决后的模型归纳,培养学生自主探究精神和合作交流意识;学生经历从观察A4 纸到探究A4 纸的设计比例的原因,感知到所学的知识和经历的实践是有实用价值的,是有益于社会的.
3 教学实录
3.1 场景呈现 提出猜想
教学情境:
教师给每位学生发一张A4 纸,并请同学们观察手中的A4 纸,猜猜其中长、宽、对角线、角度等元素之间的奥秘.
学生开展了一系列的测量、计算、数据分析等活动,在分组测量和计算长、宽的比时候,发现多个活动小组得到的长宽比稳定在1.4142857 左右.
3.2 问题提出 验证猜想
教学情境:
问题1:请大家观察这个比值(1.4142857),是否想起某个已经学过的无理数?
问题2:大家能不能提出一个猜想呢?
问题3:大家有没有办法验证这个猜想?
步骤1:利用几何画板作一个正方形,该正方
形的边长与A4 纸的宽相等;
步骤2:作该正方形的对角线;
步骤3:以该正方形的对角线为长、边长为宽作矩形;
步骤4:将A4 纸与作好的矩形重叠,并观察判断二者是否重合.
问题4:大家还有没有其他的办法?
生4:提出第二种验证操作办法,具体操作步骤如下(如图2):

图2
步骤1:将A4 纸(矩形ABCD)沿着∠BAD的平分线对折,使边AB与边AD重合,则折痕AE等于
步骤2:再沿着∠DAE的角平分线对折,并观察折痕AE与边AD是否重合.
问题5:请问你是如何想到折叠后对比这个办法的?
生4:主要是受到学生3 作图比较法的启发,验证的关键就是想办法探究A4 纸的长是不是宽的倍,沿着A4 纸的一个内角平分线折叠,得到的折痕的长度恰好是宽的倍.
3.3 数学建模 解决问题
学生经历作图、折叠、对比、观察、总结等探究过程,

这一系列问题值得深入思考.
教学情境:
教师播放介绍A 系列纸的微视频. 学生根据视频的介绍了解到若将A0 纸张沿长度方向对切成两等分,便成为A1 规格,将A1 纸张沿长度方向对切,便成为A2 规格…以此类推得到A 系列纸(如图3). A 系列纸只要A0纸的长宽比值为 2,就能保证A1、A2、A3、A4、…的长宽比值都是 2,就能保证A 系列纸只是大小不一样,形状都一样.
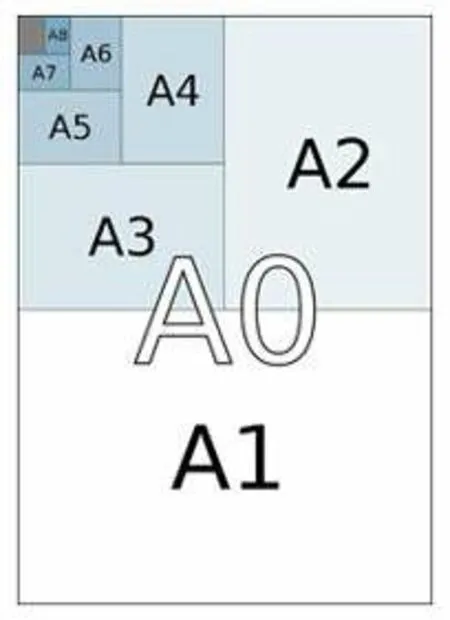
图3

3.4 模型应用 引申探究
教学情境:
问题7:A 系列纸张沿长度方向对开成两等分,折叠前后矩形的相似. 那么大家根据这个能不能提出新的问题?
生6:一张矩形纸沿长度方向三等分折叠,如果折叠前后矩形的形状相同,那么这张纸的长宽比应该是多少?

问题8:一张矩形纸沿长度方向n等分折叠,如果折叠前后矩形的形状相同,那么这张纸的长宽比应该是多少?

问题9:大家是否知道白银比例是多少?
4 教学思考
数学步道是将数学综合实践活动融入到数学学科教学的一种教学模式,如何在实际教学中开展“数学步道”式的教学呢?笔者认为应该遵循以下四点原则.
4.1 着眼数学核心素养的培养
具体的数学活动是学生数学核心素养形成的路径.“数学步道”式的课堂教学分为五个环节,概括为场景呈现→问题提出→数学建模→问题解决→模型应用. 例如本节课学生观察、测量、计算、思考,提出猜想. 学生经历作图、折叠、对比,认真验证猜想并建立数学模型. 在这一系列教师引导和学生操作的过程中,学生的数学运算、数据分析、直观想象、数学抽象、数学建模、逻辑推理等数学核心素养都得到了培养.
4.2 重视数学核心能力的提升
能力只有在需要能力的活动中才能得以培养. 在本节课的学习过程中,学生经历观测A4纸、提出猜想,能够自主测量A4 纸的长与宽、考虑长宽间的比值,根据比值联想到无理数 2,学生的数学分析观念、运算能力、数感得到锻炼和提升;在验证A4 纸的长宽比为 2 的过程中,学生的几何直观、创新意识再次得到提升.
4.3 关注学生相互之间的启发
在课堂上,老师不仅要聆听学生的回答,同时也要引导学生相互聆听、共同思考,学生的思维就像一根蜡烛点燃另一根蜡烛一样被点亮. 本节课学生4 的验证方法就是在学生3 的办法基础上改进的,思维在碰撞,灵感被激发.
雅斯贝尔斯说过“教育的本质意味着:一棵树摇动另一棵树,一朵云推动另一朵云,一个灵魂唤醒另一个灵魂”.
4.4 落实数学实际应用的功效
罗增儒教授指出“问题解决完成之后,解答依然向我们输入信息,表现为解题后的探究反思”. 本节课学生在验证A4 纸的长宽比值为后,探究了为什么A 系列纸的长宽比值都为经历探究和视频学习明确A 系列纸的长宽比值为是为了工业上的实用价值,即A 系列纸对切后形状不变性.
从A 系列纸对切后形状不变性学生猜想到“一张矩形纸沿长度方向n等分折叠,如果折叠前后两个矩形相似,那么这张纸的长宽比为这项内容如果深度思考又和“勾股螺旋图”(图4)相关.另外本节课提到了两个数列,一个是斐波那契数列(0,1,1,2,3,5,8,13,···),这个数列从第3 项开始,每一项都等于前两项之和,并且前一项与后一项的比值越来越逼近黄金比例另 一 个 是 佩 尔 数 列(0,1,2,5,12,29,···),这个数列从第3 项开始,每一项都等于前面的数的两倍加上再前面的数,并且后一项与前一项的比值越来越逼近
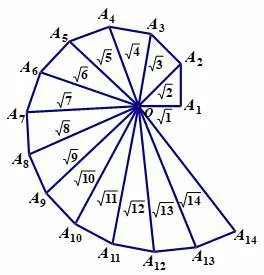
图4
5 结语
初中数学素养要在课堂真正落地,不是体现在部分学生的学习结果上,而是面对全体学生的教学过程中.《中论·上·治学》有云“学者如登山焉,动而益高”,我们将学生的数学学习过程形象为步道数学,学生经历基础知识的夯实、解题能力的提升到数学素养的形成,拾级而上,领略数学世界的美丽风光.

