高速铁路刚构矮塔斜拉桥徐变影响因素分析

王鸿飞

(中铁上海设计院集团有限公司 上海 200070)

近年来，矮塔斜拉桥以其刚度大，施工方便、经济性好的优点，在高速铁路领域得到广泛应用[1-2]。目前，建成或在建的高速铁路矮塔斜拉桥主要有商合杭铁路(94.2 m+220 m+94.2 m)颖上特大桥、黄冈至黄梅铁路(108 m+200 m+200 m+108 m)巴河特大桥、赣深客专(136 m+260 m+136 m)剑谭东江特大桥、池黄高速铁路(48 m+118 m+2×228 m+118 m+48 m)太平湖特大桥[3-4]等。

高速铁路对线路的平顺性要求远高于普通铁路，对于无砟轨道，没有道砟来调节轨道高度，后期只能通过扣件调整，由于扣件可调节量有限，后期调轨困难，所以必须严格控制铁路后期变形[5-6]。因而大跨度无砟轨道桥梁的工后徐变成为计算过程中的主要控制因素之一，在规范中对工后徐变的数值进行了严格的规定。

1 工程背景

1.1 工程概况

本文依托工程为新建淮北-宿州-蚌埠城际铁路淮河特大桥主桥，为刚构体系矮塔斜拉桥，计算跨径为(124 m+248 m+124 m)，全长497.5 m，为塔梁墩固结体系。桥面板宽14.3 m，塔梁墩固结处局部加宽至18.3 m。

主墩采用双薄壁实体截面，顺桥向宽度2.7 m，双薄壁间距3.6 m，横向宽度15.5 m。主墩承台顺桥向×横桥向×厚度为21.6 m×21.6 m×6 m，桩基础采用16根直径2.8 m钻孔灌注桩，按柱桩设计。

边墩采用圆端形实体桥墩，墩底截面尺寸4.0 m×14.2 m(顺桥向×横桥向)，承台尺寸8.4 m×18.8 m×4.0 m(顺桥向×横桥向×厚)，基桩采用8根直径2.0 m 的钻孔灌注桩，按柱桩设计。桥型布置图见图1。

图1 淮河特大桥主桥桥型布置图(单位：cm)

1.2 主桥截面设计

梁体截面为单箱双室、变高度、变截面箱梁，顶板、底板、腹板局部向内侧加厚，按线性变化。中支点截面梁高为13.0 m，跨中直线段及边跨直线段梁高6.0 m，梁底下缘按二次抛物线变化。桥面以上塔高47.1 m，最上排斜拉索理论锚固点距离桥面44 m，塔梁高跨比为1/5.636。主桥箱梁截面见图2和图3。

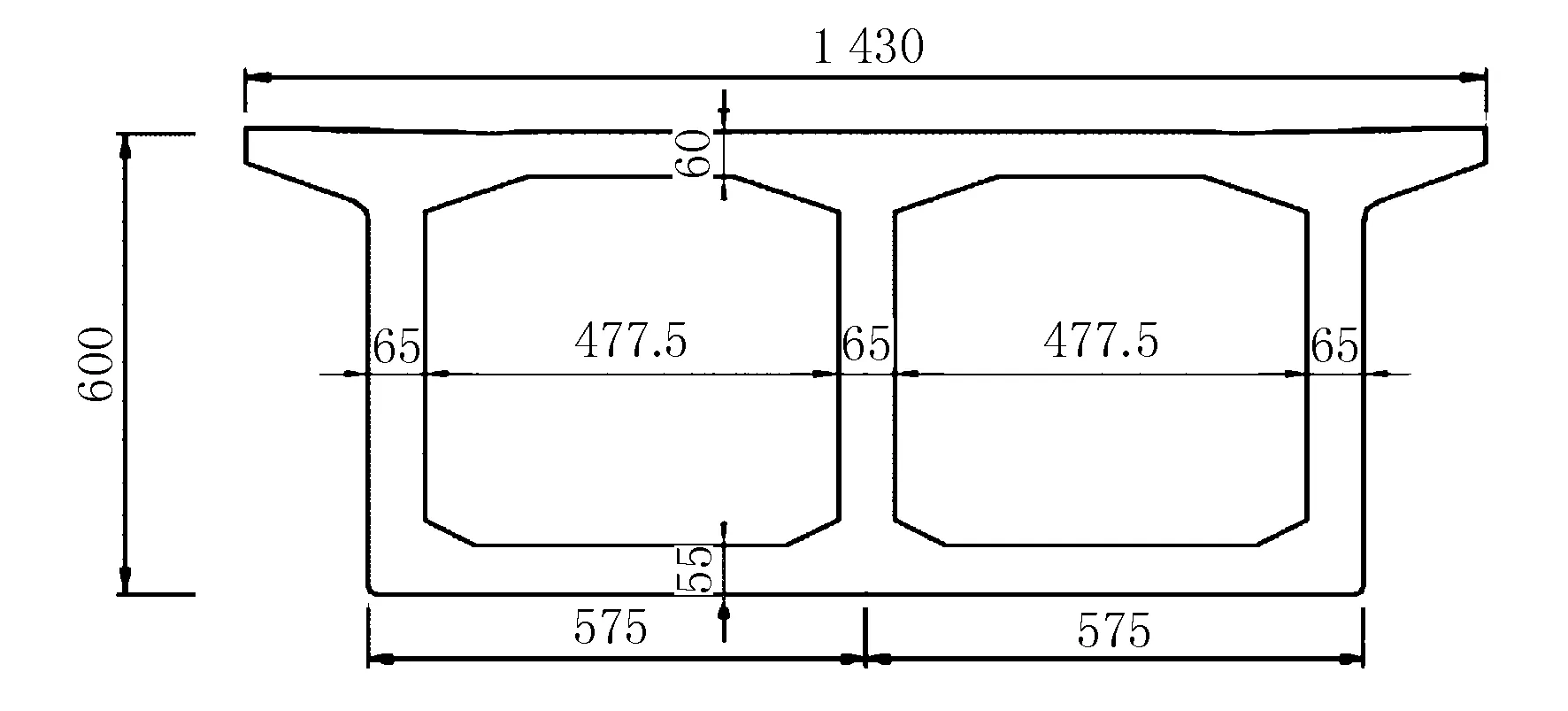
图2 箱梁跨中等截面图(单位:cm)

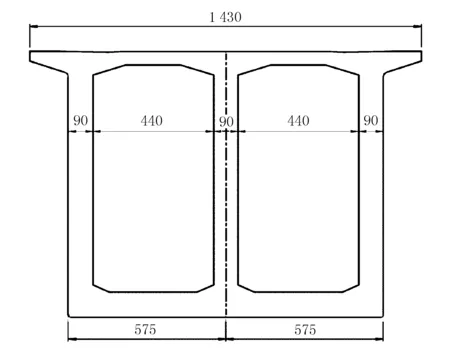
图3 箱梁变截面图(单位:cm)

1.3 有限元模型

采用有限元软件midas Civil建立空间杆系计算模型。主梁、桥塔、桥墩和承台、桩均采用梁单元模拟，斜拉索采用桁架单元模拟，有限元模型见图4。

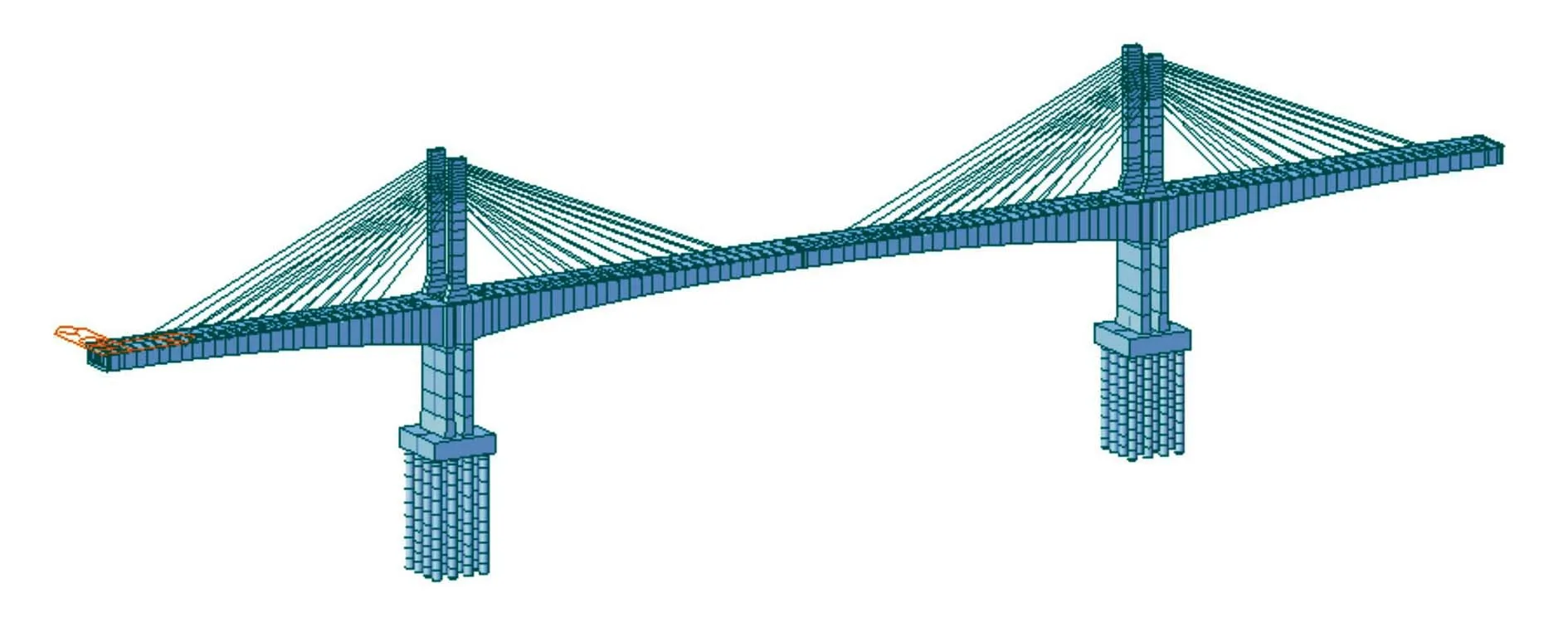
图4 有限元模型

2 徐变系数及延续期选取

桥梁徐变系数取值，国内主要规范依据有TB 10092-2017 《铁路桥涵混凝土结构设计规范》(以下称《TB 10092规范》)和JTG 3362-2018 《公路钢筋混凝土及预应力混凝土桥涵设计规范》(以下称《JTG 3362规范》)。

《TB 10092规范》中规定徐变系数计算方法如式(1)。

φ(t,τ)=βa(t)+0.4βd(t-τ)+φf[βf(t)-βf(τ)]

(1)

式中：φ(t,τ)为徐变系数；βd(t-τ)为随时间增长的滞后弹性应变；φf为流塑系数；βf(t)、βf(τ)为随混凝土龄期增长的滞后塑性应变，与理论厚度有关。

其中，βa(t)计算方法见式(2)。

(2)

式中：fτ为混凝土龄期为τ的强度；f∞为最终强度。

计算龄期与加载龄期差值大于1 000 d后，混凝土强度变化引起应变和滞后弹性应变为常量，塑性应变随着时间的增加继续增大。

《JTG 3362规范》中规定徐变系数计算方法见式(3)。

φ(t,t0)=φ0·βc(t-τ)

(3)

式中：φ(t,t0)为加载龄期为t0时，计算考虑龄期为t时的混凝土徐变系数；φ0为名义徐变系数；βc(t-τ)为加载后徐变随时间发展系数。

《JTG 3362规范》规定延续期为10年。根据熊志朋等[5]的研究，实测跨中徐变与规范值吻合较好。

针对(124 m+248 m+124 m)矮塔斜拉桥徐变系数及延续期，分别按3种方案进行计算。

方案一：采用公路《JTG 3362规范》延续期10年。

方案二：采用铁路《TB 10092规范》延续期1 000 d。

方案三：采用铁路《TB 10092规范》延续期10年。

计算结果见图5。

图5 不同规范及延续期徐变

由图5可以得到以下结论：

①铁路规范延续期10年工后徐变最大，为跨中-19.4 mm(负号表示方向向下，后同)；②铁路规范延续期1 000 d与公路规范延续期10年跨中工后徐变接近，分别为-14.1 mm和-14.7 mm。

3 徐变影响因素分析

矮塔斜拉桥塔高、索力、无索区长度，以及预应力均会影响结构的受力状态，进而影响结构的徐变。

3.1 塔高对徐变影响

随着桥塔高度增加，拉索的倾角增大，其竖向支承能力提高。针对本桥最外排斜拉索理论锚固点距离桥面不同，设计比较了4种方案。

方案一：索塔高度40.0 m。

方案二：索塔高度42.0 m。

方案三：索塔高度44.0 m。

方案四：索塔高度46.0 m。

徐变计算结果见图6。

图6 塔高-徐变影响图

由图6可以得到以下结论。

①矮塔斜拉桥索塔高度的变化对跨中徐变影响明显，在索塔40～46 m范围内，随着矮塔斜拉桥塔高度增加，跨中弯矩减小，上翼缘应力减小，下翼缘应力增加，跨中工后徐变变小。塔高增加15%，徐变减少52.7%。

②索塔高度的变化对边跨徐变影响不明显。

③在满足拉索疲劳性能要求和桥塔受力合理的前提下，可以通过增加矮塔斜拉桥塔高减小跨中工后徐变。

3.2 索力对徐变影响

随着斜拉索索力增加，拉索承担的竖向荷载比例随之增大。保持斜拉索根数及面积不变，改变斜拉索索力，设计了3种方案进行比较。

方案一：90%斜拉索索力。

方案二：1.0倍斜拉索索力。

方案三：1.1倍斜拉索索力。

徐变计算结果见图7。

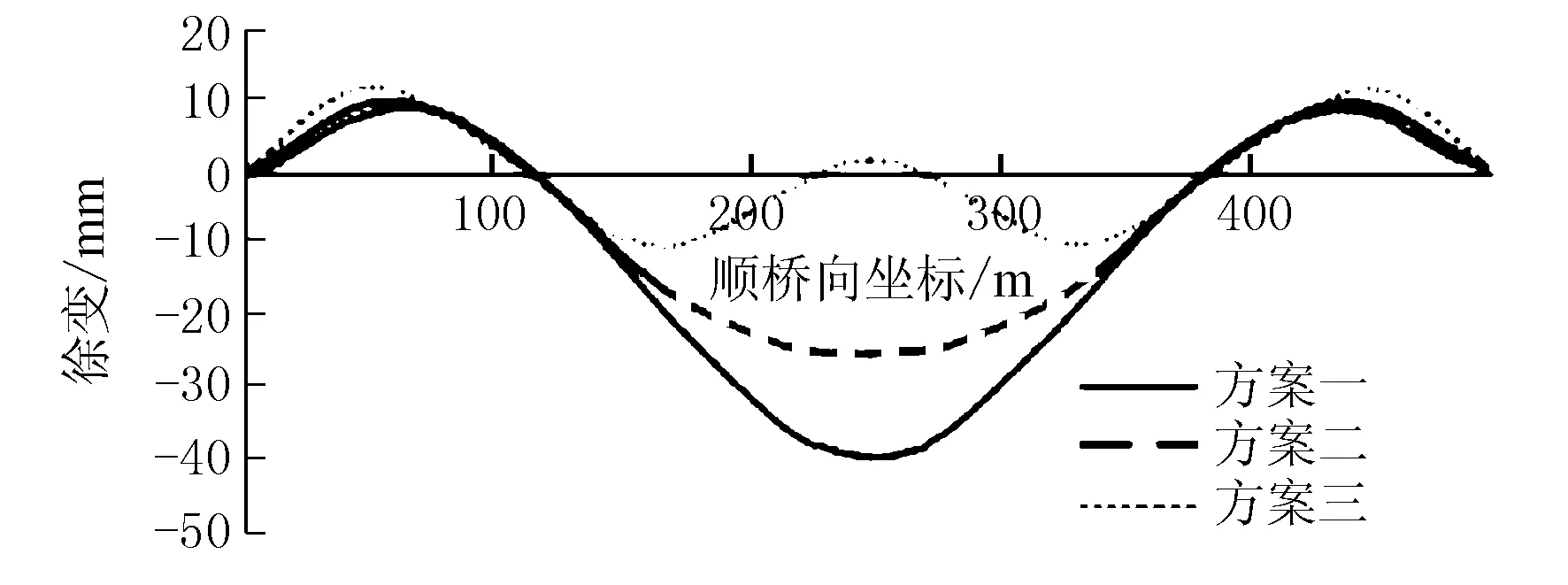
图7 斜拉索索力-徐变影响图

由图7可知，矮塔斜拉桥索力对跨中工后徐变影响明显。随着斜拉索索力的增加，跨中弯矩减小，上翼缘应力减小，下翼缘应力增加，徐变降低。索力增加22.2%，工后徐变减少73.5%。当索力增加到一定数值时，跨中工后徐变由下挠变为上拱。

3.3 无索区长度对徐变影响

矮塔斜拉桥无索区比一般斜拉桥要长，主梁有3处无索区，即边跨无索区、塔旁无索区和跨中无索区。针对本桥无索区长度，保持斜拉索根数及索力不变，设计比较以下3种方案。

方案一：塔旁无索区长度50.2 m，边跨无索区长度26.9 m，跨中无索区长度53.8 m。

方案二：塔旁无索区长度66.2 m，边跨无索区长度18.9 m，跨中无索区长度37.8 m。

方案三：塔旁无索区长度82.2 m，边跨无索区长度10.9 m，跨中无索区长度21.8 m。

徐变计算结果见图8。

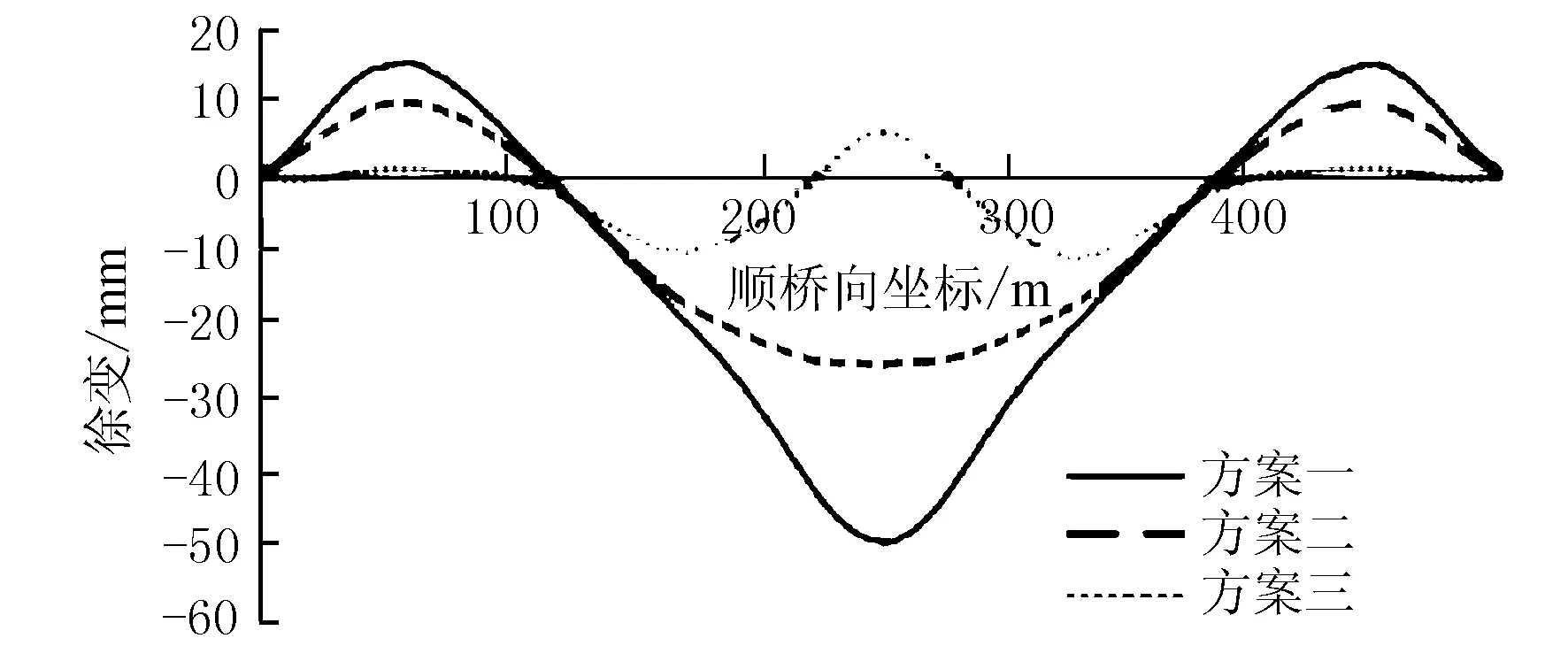
图8 跨中无索区长度-徐变影响图

由图8可知，矮塔斜拉桥跨中无索区长度对中跨工后徐变影响明显。跨中工后徐变随跨中无索区的长度缩短而减小。当跨中无索区长度减小到一定数值时，跨中工后徐变由下挠变为上拱。跨中无索区长度减少40.5%，跨中工后徐变减少77.6%。

3.4 预应力钢束对徐变影响

预应力钢束通过改变截面应力分布影响徐变。预应力钢束分为腹板钢束、边跨底板钢束、中跨底板钢束、中支点顶板钢束及边跨顶板钢束。

3.4.1腹板预应力钢束对徐变影响

保持张拉应力不变，修改腹板预应力钢束的面积。对以下3种方案进行比较。

方案一：采用80%腹板预应力钢束面积。

方案二：采用实际腹板预应力钢束面积。

方案三：采用1.2倍腹板预应力钢束面积。

计算结果见图9。

由图9可知，腹板束的变化对跨中徐变影响不明显，随着腹板预应力钢束面积增加，梁体跨中徐变略有减小。

3.4.2边跨底板预应力钢束对徐变影响

保持张拉应力不变，改变边跨底板钢束的面积。对以下3种方案进行研究。

方案一：采用80%边跨底板预应力钢束面积。

方案二：采用实际边跨底板预应力钢束面积。

方案三：采用1.2倍边跨底板预应力钢束面积。

计算结果见图10。

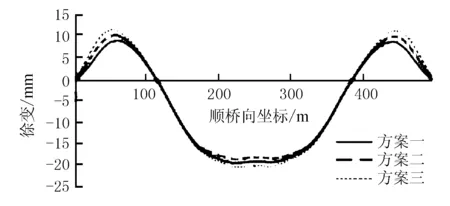
图10 边跨底板预应力钢束-徐变影响图

由图10可知，边跨底板束的变化对跨中徐变几乎无影响。

3.4.3中跨底板预应力钢束对徐变影响

保持张拉应力不变，修改中跨底板预应力钢束的面积。按以下3种方案进行比较。

方案一：采用80%中跨底板预应力钢束面积。

方案二：采用实际中跨底板预应力钢束面积。

方案三：采用1.2倍中跨底板预应力钢束面积。

计算结果见图11。

图11 中跨底板预应力钢束-徐变影响图

由图11可知，中跨底板预应力钢束的变化对跨中工后徐变影响明显。跨中工后徐变随中跨底板预应力钢束面积增加而减小。中跨底板预应力钢束面积增加50%，跨中工后徐变减少38.7%。

3.4.4中支点顶板预应力钢束对徐变影响

保持张拉应力不变，修改中支点位置顶板预应力钢束的面积。按以下3种方案进行比较。

方案一：采用80%中支点顶板预应力钢束面积。

方案二：采用实际中支点顶板预应力钢束面积。

方案三：采用1.2倍中支点顶板预应力钢束面积。

计算结果见图12。

图12 中支点顶板预应力钢束-徐变影响图

由图12可知，中支点顶板预应力钢束的变化对跨中工后徐变影响明显。跨中工后徐变随顶板预应力钢束面积增加而减小。中跨底板预应力钢束面积增加50%，跨中工后徐变减少41.7%。

3.4.5边跨顶板预应力钢束对徐变影响

保持张拉应力不变，修改边跨顶板预应力钢束的面积。设计比较了3种方案。

方案一：采用80%边跨顶板预应力钢束面积。

方案二：采用实际边跨顶板预应力钢束面积。

方案三：采用1.2倍边跨顶板预应力钢束面积。

计算结果见图13。

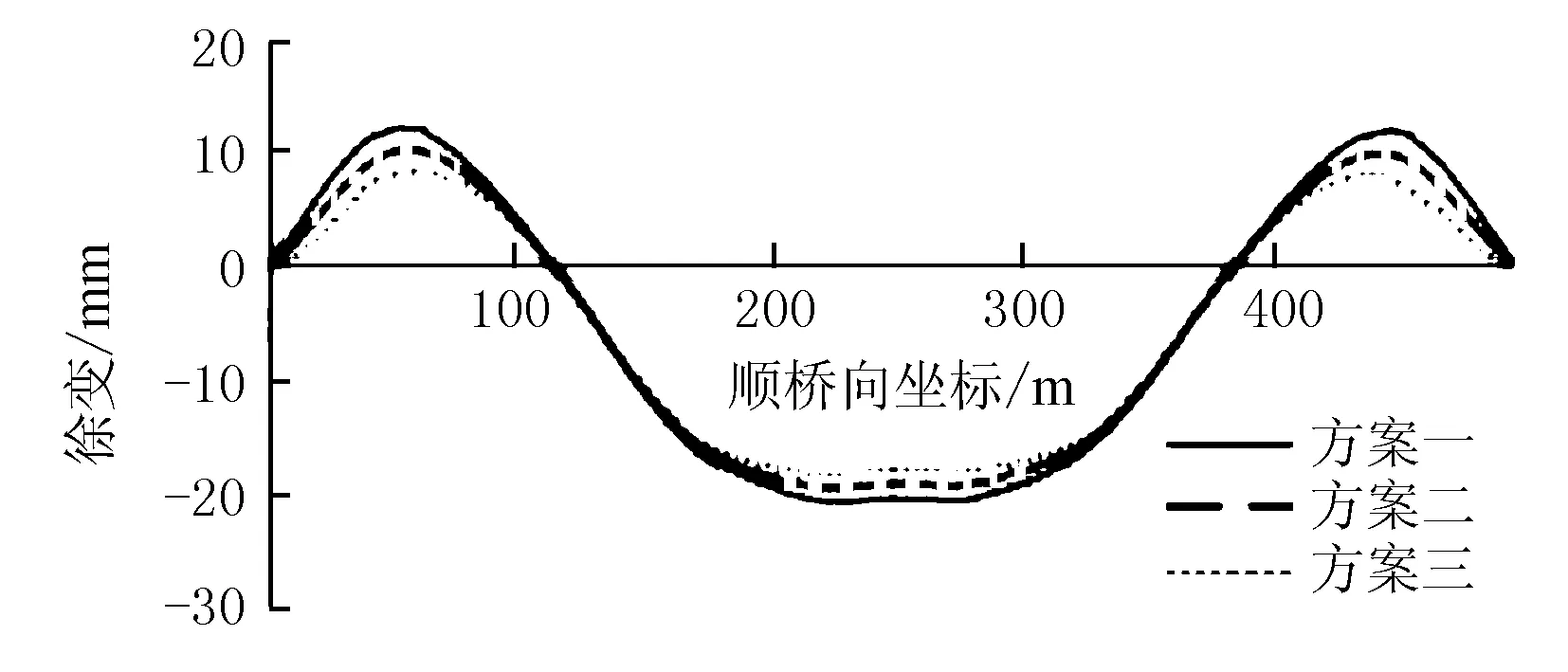
图13 边跨顶板预应力钢束-徐变影响图

由图13可知，边跨顶板预应力钢束面积的变化对跨中工后徐变影响甚微。

4 结语

高速铁路无砟轨道对工后徐变有着严格的要求，大跨度桥梁的工后徐变控制对结构尺寸的拟定和设计影响甚大。本文通过分析得到了针对刚构矮塔斜拉桥的如下结论。

1) 铁路规范采用1 000 d延续期与公路规范采用10年延续期计算所得跨中徐变接近，铁路桥涵计算采用1 000 d延续期计算较为合理。

2) 在满足结构设计合理的条件下，可以增加斜拉桥塔高、提高索力和减小跨中无索区长度，改善结构跨中的受力状态，增加下翼缘应力，进而减小矮塔斜拉桥跨中徐变。

3) 适当增加中支点顶板预应力钢束和跨中底板预应力钢束，可以改善矮塔斜拉桥跨中截面应力，进而达到减小跨中徐变的目的。