养护干预下车道级沥青路面表面性能演变模型*

汪 蓉 叶文亚

(1.同济大学道路与交通工程教育部重点实验室 上海 201804; 2.宁波工程学院建筑与交通工程学院 宁波 315211)

路面在使用过程中，受到车辆荷载和环境因素的共同作用，使用性能随着时间不断降低，裂缝、车辙等路面损坏随之出现。基于路面技术状况的检测评估结果，对路面实施日常养护、预防养护、修复养护等措施，可达到提升路面性能水平、延缓性能衰变速率、延长路面使用寿命的目的[1]。为此，预测路面在养护干预后使用性能随时间变化的规律至关重要。

国内外已提出多种路面性能预测模型，采用的方法可归为4类：确定性方法、不确定性方法、仿生方法及动态方法[2]。AASHTO中的路面服务能力方程[3]和国内孙立军[4]提出的路面使用性能衰变方程均为基于经验回归法建立的确定性模型；不确定模型中较为常用的为马尔科夫模型，刘伯莹等[5]应用马尔科夫过程建立了网级路面使用性能概率预测模型，路明[6]提出了特定养护措施下路面性能的双参数曲线和灰色系统理论+马尔可夫转移概率衰变模型；仿生方法指神经网络法，神经网络具有良好的非线性品质，适合处理路面性能预测中复杂的环境因素[7]；动态方法主要为时间序列法，武建民等[8]分析了路面养护维修后使用性能衰变的影响因素，建立基于时间序列分析法的ARIMA模型。

虽然以往的研究成果已较为丰富，但建立的各模型都存在其适用性和一定的局限性。当前对于不同的道路条件难以提出统一适用的预测模型。特别是当检测数据不完整、养护资料不详细、检测与养护信息不匹配时，一些模型会丧失其有效性。本文正视这种复杂性，优选符合路面性能衰变规律、具有明确物理背景的衰变方程，并结合养护信息和新的测试数据，提出模型参数的动态调整方法，以应对现实道路管养的情况。

1 路况介绍

1.1 工程概况

某高速公路全长58.7 km，双向六车道，设计行车速度为120 km/h。路面结构形式为：4 cm AC-13C(SBS改性)上面层+6 cm AC-20C(SBS改性)中面层+8 cm AC-25C下面层+水泥稳定碎石基层。该高速于2007年12月正式通车，通车已超过10年，病害以路面横向裂缝为主，包括水泥稳定碎石基层的反射裂缝和路面面层的疲劳裂缝；局部路段存在坑洞、块状裂缝和纵缝病害。

1.2 检测活动与养护历史

2015-2018年，利用多功能检测车对该高速公路进行每年1次的路面技术状况检测，并根据JTG 5210-2018 《公路技术状况评定标准》[9]，对路面使用性能进行评价。基于路面损坏状况指数PCI衰退规律显著的特点，多用于控制沥青路面维修养护的触发指标[10-11]，本文选用PCI历史检测数据作为研究对象。

检测范围为双向六车道，共352.2 km，以1 km为单位输出PCI。故本文将每公里作为1个单位路段，每车道共59个单位路段(最后700 m不足1 km视为1个单位路段)。据历史养护资料，2015-2018年间，每年该高速公路均有不同的单位路段实施养护维修活动。

2 未养护时路面性能衰变方程

2.1 衰变方程标定方法

综合比较各模型特点及适用条件，结合现有项目检测数据及养护资料不齐全的现状，本文选取符合路面性能衰变规律、具有明确物理背景的路面性能标准方程作为基础模型进行标定，计算方法见式(1)。

(1)

式中：PCI0为初始PCI；t为路龄；α及β为模型参数，其数值由路面实测数据回归得到，其中，α为寿命因子，反映路面使用寿命的长短，β为模式因子，反映衰变曲线的形状。

本文利用R语言nls函数拟合已确定方程形式的非线性模型。该函数针对式(1)中的待估参数α、β，采用Gauss-Newton法数次迭代，多次修正回归系数，寻找最逼近非线性模型的参数最优值，使得模型的残差平方和达到最小。参数初始值设置对模型求解至关重要，不合适的初始值会造成迭代不收敛或返回无意义的参数值。本文选取任意2年数据对式(1)进行线性反解作为参数初值，可有效提高模型拟合的效率和精度。

2.2 检测数据分析

按照衰变规律，未对路面实施养护措施时，PCI会不断降低；经历养护维修后，PCI明显提升，随后逐渐衰减。对该高速公路每车道各单位路段的检测数据与养护资料综合分析，发现出现“异常”情况：未实施养护措施的路段，PCI突然提升，少则波动0.05，多则提升至100。该情况可能是由路面性能检测条件波动、养护维修信息不详细等原因造成的。

在建立单位路段路面衰变方程时，这些异常路段模型拟合效果较差，无法回归出衰变曲线，只能剔除，各车道养护率及可标定路段占比，见表1。

表1 各车道养护率及可标定路段占比

由表1可见，可标定的路段数量减少，导致无法建立未养护时各路段的自然衰变方程。为有效利用现有检测数据，本文将建立车道级路面性能衰变方程。

2.3 车道级路面性能衰变方程

针对上述在未养护路段中发现的“异常”路段，剔除PCI突增到100及增幅大于5的单位路段，将其归类于养护路段。对于剩下的未养护单位路段，计算得各车道历年PCI平均值，结果见表2。

表2 未养护时各车道历年PCI平均值

依据2.1节的标定步骤，建立未养护时车道级沥青路面性能衰变方程，并对模型精度进行检验，结果汇总于表3。

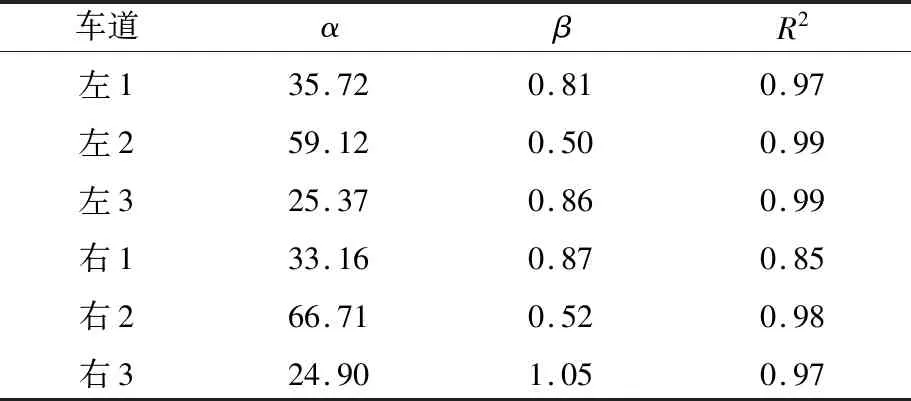
表3 未养护时路面性能衰变方程标定结果

由表3可知，各车道路面性能衰变方程的拟合优度R2均接近于1，说明模型的拟合优度较好。绘制路面性能衰变拟合曲线见图1。

图1 未养护时各车道路面使用性能

综合表3和图1分析可知，各个车道路面性能衰变均属于先慢后快的模式。该模式说明在路面服役初期，路面性能较好，即使在车辆荷载和环境因素的共同作用下，也能保持较低的衰变速率。随着时间的推移，路面结构性损坏增多，路面抵抗荷载的能力下降，衰变速率加快。此外，该高速公路通车后历年均会进行日常养护，也是其初期保持较高路面性能水平的原因之一。

对车道进行分析，发现左3车道和右3车道的寿命因子回归值接近，且均小于其他车道，说明其路面使用寿命短于其他车道。从图1中也可清晰看出，左3和右3车道的衰变曲线更陡峭，衰变速率更快。各车道路面结构形式一致，荷载差异对不同车道路面破损产生影响。而相较于其他车道，3车道交通量更大、重载车多，加剧了路面破坏。

3 养护干预下路面性能衰变方程

3.1 斜率法确定衰变速率改变

当养护实施以后，路面表面性能明显提升，PCI检测值变大。但由于只是表层修复，其内部结构破坏仍会在一定时间以后反射到路表，只是时间上与养护前有所区别。提升后的性能衰变速率会低于同时点的衰变速率、高于同性能水平对应时点的衰变速率。反映在模型上为PCI演变时的斜率不同。

绘制衰变速率调整示意图见图2。

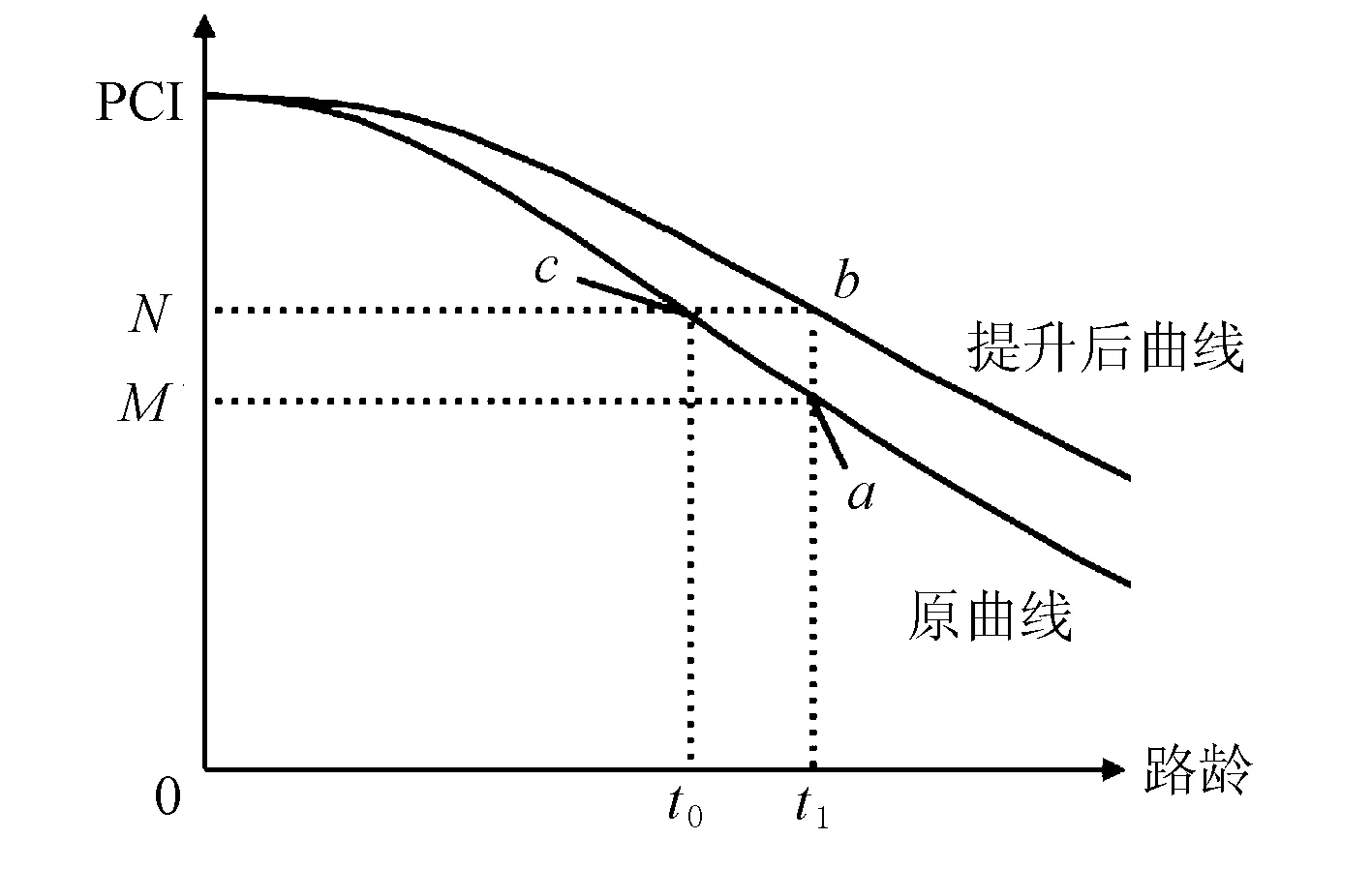
图2 衰变速率调整示意图

由图2可见，t1时PCI值为M，路面经过养护活动后，性能提升至N。过b点做直线相交于原曲线c点，此时刻为t0。提升后曲线在t1时刻b点的斜率大于k原曲线a点的斜率k1，小于原曲线在t0时刻c点的斜率k0。如果时间跨度不长，则可以简单选择这2个时点的均值；如果时间跨度比较长，则可以根据一定的权重分配。

3.2 养护后路面性能衰变方程

依据养护后路面性能衰变曲线斜率的变化，确定提升后路面性能衰变曲线的方程。具体计算步骤如下。

1) 已知养护前原曲线方程Y0为式(2)，t1时刻PCI值为M。养护后PCI值为N，根据式(3)可求出。

(2)

(3)

式中：α0、β0为养护前衰变模型参数值。

2) 时间跨度t1-t0不大时，令t1时刻性能提升后的斜率k=(k0+k1)/2。k2和k1由R语言eval函数在t0和t1时刻对式(1)求导计算可得。

3) 养护时间相近，路面性能衰变模式不会发生巨大改变，即假设β不变。养护后路面性能方程Y需同时满足以下关系。

(4)

式中：Y′(t1)为养护后方程Y在t1时刻的导数。

联立上述2个方程，如式(5)所示，即可求得养护后方程模型参数值。

(5)

式中：α为养护后寿命因子；β为养护后模型因子，β=β0。

3.3 养护后路面性能衰变方程迭代

由于每年养护路段不同，如某单位路段4年间连续被养护，而有些路段只在某一年实施了养护措施。考虑该情况，本研究以无后效性为原则，即第n年路面性能衰变方程已知，则第n+1年的衰变方程仅与第n年有关，而与其在第n年以前所经历的状态无关。依据第n+1年是否养护，决定是否对方程进行修正，如式(6)所示。

(6)

式中：Yn+1为第n+1年衰变方程；Yn为第n年衰变方程；修正Yn为第n+1养护后，基于3.2节斜率法对Yn修正所得。

3.4 案例分析

以该高速公路左三车道为例，依据上述步骤可迭代出2018年不同路段的路面性能衰变方程，迭代流程见图3，结果见表4。以2018-1方程及2018-4方程为例，分析不同养护条件下路面性能衰变规律，衰变曲线见图4。

图3 路面性能方程迭代流程

表4 左3车道历年路面衰变方程

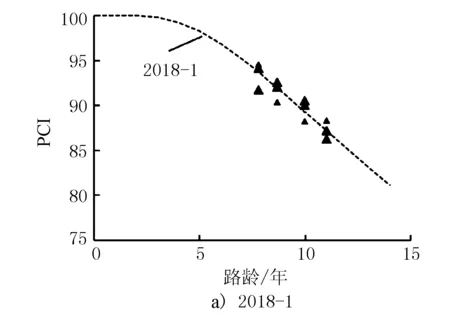
图4 养护后路段2018年PCI衰减曲线

分析2018-1方程可知，2015-2018年4年间均未实施养护措施的路段适用于该模型。将这些路段实测值绘制于图4a)，可看出实测值与该曲线较为吻合。

分析2018-4方程可知，只有2016年及2017年实施养护措施、其他年份未养护的路段适用于该模型，实测值与预测曲线关系见图4b)。

由图4可见，2015年未养护时，这些路段PCI实测值与2018-1的自然衰变曲线接近；2016及2017后实施养护措施后，实测值提升，且抬升后曲线的路面衰变速率要缓于2018-1；2018年未养护时，路面继续衰变，PCI实测值与2018-4曲线吻合，说明由斜率法反算得到的衰变方程具有可靠度。

之后可借助2018-4方程辅助养护决策。一方面可直接预测出之后的路面性能水平，判断是否需要进行维护；另一方面，当考虑实施养护计划时，例如使用超薄磨耗层进行预养护，依据工程经验PCI将提升2～3分值，则可依据斜率法求得实施养护措施后的路面性能衰变方程，评价养护后的路面性能衰变规律，为养护措施的选择提供参考。

4 结论

1) 针对路面性能检测数据不足、养护信息不完整，无法建立单位路段路面性能预测模型的情况，有效利用现有数据建立了未养护时车道级路面性能预测模型。该模型与实测值的拟合度较高，预测的详细度也好于将整幅路面作为整体进行预测。

2) 将养护干预后路面性能的提升、衰变速率的减缓抽象为衰变曲线斜率的变化，实现了对养护干预后路面性能模型的建立。该模型计算简单，且具有物理意义。

3) 依照无后效性原则对路面性能方程进行迭代，得到最新的路面性能方程，从而对符合条件的路段进行预测，不仅提升了预测的可靠性，也重新由车道级方程转变为单位路段级，更有利于养护计划的制定。