改进的永磁同步电机模型预测控制方法

周浪 郑锦楠

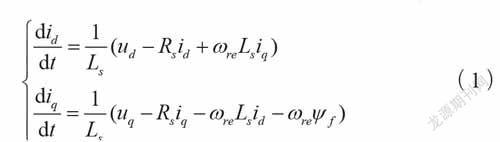
关键词：永磁同步电机;改进预测控制;电流畸变

随着国家提出推动运输工具装备低碳转型，越来越多新能源的电动汽车厂商崛起，鉴于目前电动汽车的动力系统通常都是PMSM驱动系统，因此PMSM的发展前景十分广阔。在众多的电机控制方法中，直接转矩控制和矢量控制以往研究较多，但随着控制精度的要求越来越高，这两种控制方法以难以满足响相应的要求。而MPC因为设计方便、响应快、动态性能好等优点，近年来备受关注，在PMSM中得到了广泛的应用。应用于电力电子的MPC主要有两种：连续集模型预测控制（continuouscontrolsetmodelpredictivecontrol，CCSMPC）和有限集模型预测控制（finitecontrolsetmodelpredictivecontrol，FCS-MPC）。CCS-MPC计算利用优化问题的解决方案，并且调制级生成转换器致动的开关状态。FCS-MPC利用功率变换器的离散特性和负载模型来彻底解决优化问题[4]。然而，传统的FCS-MPC也存在一些缺点，比如电流精度不够高、电磁转矩响应不够快。

本文介绍了一种通过选择最佳有效矢量时间来进行改进的方法，提高电流的跟踪精度以及减少电流畸变率。并用仿真分析验证改进后方法的有效性。

1永磁同步电机的数学模型

忽略磁滞损耗、涡流、铁芯饱和，另LLLdqs==，PMSM在同步旋转坐标系下的电压方程表示为：

2模型预测控制原理

2.1传统模型预测控制原理

将等式（1）离散化后得到预测模型，如等式（2）-等式（5）

其中，Ts为采样周期;ukd（）和ukq（）分别为k时刻的d、q轴电压值;ωre（k）为k时刻的转子电角速度。

电压矢量空间中六个基本电压有效矢量（u～u）16的模均小于母线直流输入端电压的二/3，从而可得到最优作用时间。通过代价评估函数求得基本电压矢量落于各区域，圆形矢量空间中的所有基本电压矢量位置以及导通时间将如表一所给出

对于两电平三相电压源逆变器，共有6个有效基本电压矢量（u～u）16和2个零矢量（u，u）07。将k时刻8个基本矢量所对应的ikd（）、ikq（）带入等式（2）即可求出ikd（+1）、ikq（+1）。

将价值函数gi设为电流预测值（ikd（+1）、ikq（+1））与电流给定值（id*、iq*）之差后，即可得到最佳电压矢量，gi表示为

将（ikd（+1）、ikq（+1））代入等式（6）后就可以計算出相应的g值，并将最小的g值作为最佳电压矢量输出。

2.2改进的模型预测控制原理

针对传统FCS-MPC的控制精度不够高和电磁转矩响应不够快这一关键问题。本文将介绍了一种较为简单的提升方法，该方法通过把可选择的最佳有效矢量时间也加入了这一过程中，从而产生了显著提升控制精度，使在开关条件下的电子运动更加规律并减少了电气噪声的产生。

将等式（2）恒等变换为：

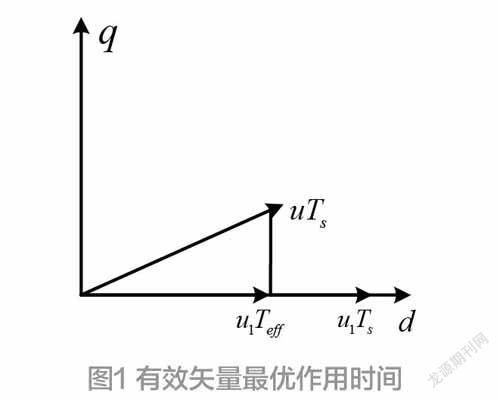
等式（7）通过k时刻的d、q轴的电流值，预测出PMSM模型输出电压的估计值，并将三相并网逆变器输出电流按照给定最佳有效电压矢量进行输出。如图1所示，按照以往的传统算法u1将为最优矢量，但是根据伏秒平衡原理可以得出，作用时达不到最好的跟踪效应。而通过图中方法可以得出电压矢量的最佳时间应为Teff，再根据该原理可以得到本文所提到的优化方案。

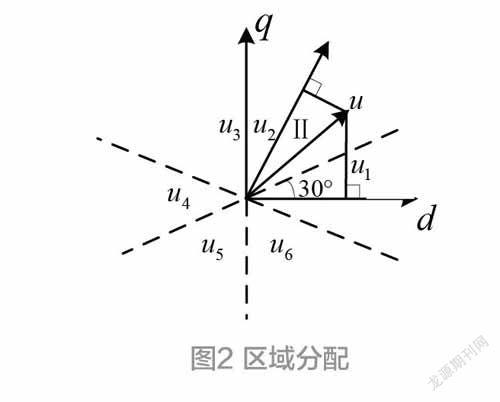
改进后的算法其关键在于有效矢量的选取及其作用时间，再选取零矢量及确定开关状态。最优的有效矢量选择及作用时间可以提高电流跟踪精度，选取零矢量及确定开关状态则可以让开关频率更低。而有效矢量的选择需要通过矢量区域确定，如图2所示。

从图2可以看出，两条虚线和d、q轴将平面分为六个不同的区域，每个区域对应不同的电压矢量。电压矢量的选择对应于电压矢量在区哪个域。例如，当电压矢量u在Ⅱ区域，经简单的几何原理可知，电压矢量u的端点距离电压矢量u2的方向更近，此时就应选择u2作为下一周期的有效矢量。

相较于以往传统的模型预测控制算法，文章提出的改进后的算法与其不同的一点在于需要计算矢量的最佳作用时间，具备较高电流控制精度和开关管状态变化规律。如图3所示。

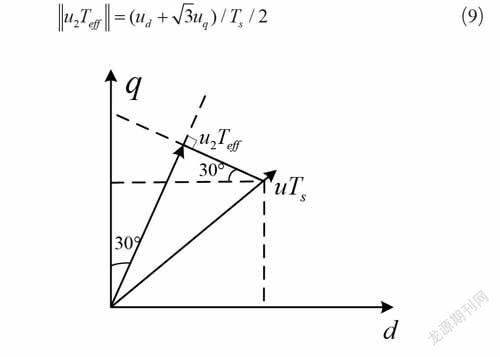
如图3所示，电压矢量在Ⅱ区域时，即应选择u2作为有效矢量，但是选择的最佳有效时间Teff可以通过下式确定：

永磁同步电机6个基本电压有效矢量（u～u）16的模均小于三相并网逆变器直流输入电压的2/3，从而可得到最优作用时间Teff。6个基本电压有效矢量均按照上述步骤进行类推，则永磁同步电机矢量位置以及占空比计算时间将如表1所给出。

3仿真与实验

为验证上文所述方法的有效性，用Matlab/Simulink对传统的模型预测算法和改进之后的模型预测算法进行比较仿真验证。为了说明改进后模型预测算法的有效性，两种模型预测算法的算法不同，但是仿真参数设置一致，仿真参数如表2所示。

仿真条件的设置为：电机以3N·M启动，给定转速为1000r/min，在运行至0.2s时将转速升至1200r/min，运行至0.4s，转速降为1000r/min，在运行至0.6s时加负载至8N·M，一直运行至0.8s，将负载降至4N·M，总共的仿真时间为1s。观察其电磁转矩响应、速度响应、定子电流响应波形图。

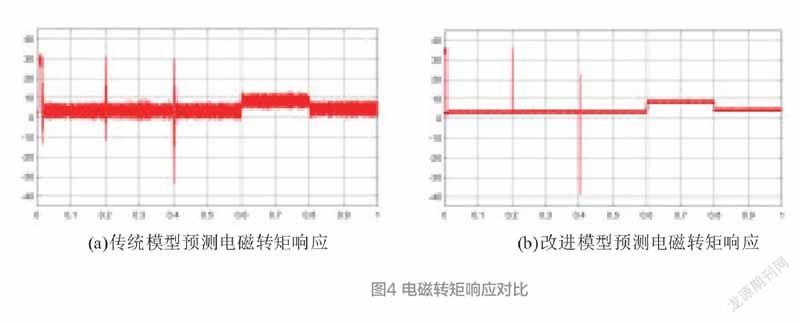
分析图4，从整体上可以清晰看出，相比与传统模型预测，改进后的模型预测电磁转矩响应在受到负载变化时，电磁转矩能瞬时达到给定的负载值，并且在其给定值的附近只有很小的波动。

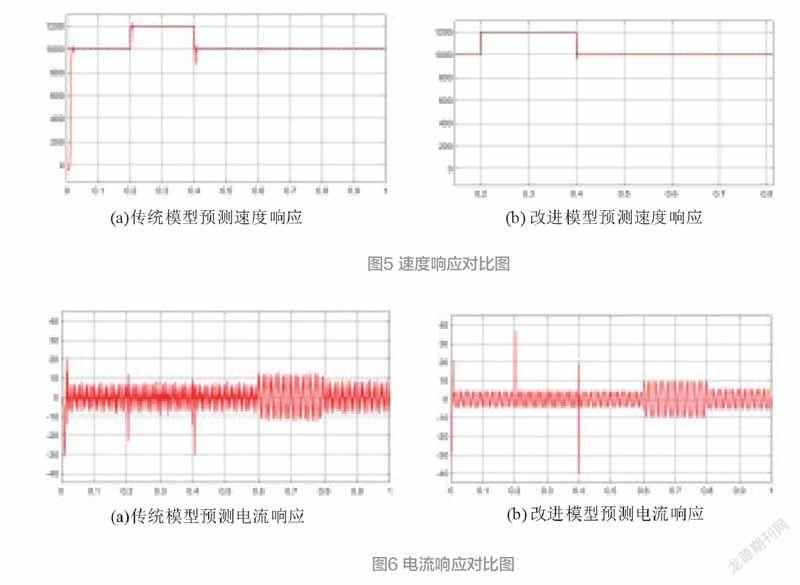
分析图5，传统的模型预测速度响应在0.0165s时才达到峰值，超调量达到2.7%，当0.2s时转速时转速升至1200r/min时，至0.2025s时才达到峰值，超调量达到2.3%。当0.4s时再次将转速降至1000r/min，至0.402才达到给定值，并且超调量高达12%。分析改进的模型预测速度响应，当0.2s时转速时转速升至1200r/min时，至0.2045s时就达到峰值，超调量只有0.6%。当0.4s时再次将转速降至1000r/min，仅0.401s就达到给定值，并且超调量只有3%。对比可以明显发现，相比与传统的模型预测，改进后的模型预测其速度响应明显更快。

分析图6，从整体上可以清晰看出，相比与传统模型预测，改进后的模型预测电流响应速度在受到负载变化时，电流纹波更小，毛刺更少，电流畸变率更低，噪声更小。

综上所述，改进后的模型预测，不管是在电磁转矩响应、速度响应还是电流响应方面，都比传统的模型预测更好。改进后的模型预测提高了电流的跟踪精度，减少了毛刺以及减小了电流的畸变率。