高速列车智能轮对应力谱测试及车轴裂纹扩展寿命分析

王文静，闫瑞国，丁然，张振先，沙淼，单巍

(1.北京交通大学载运工具先进制造与测控技术教育部重点实验室，北京，100044；2.中车青岛四方机车车辆股份有限公司，山东青岛，266111；3.中车长春轨道客车股份有限公司，吉林长春，130062；4.中国国家铁路集团有限公司，北京，100844)

截至2020 年底，我国动车组保有量达3 900列，车轴装车量超过10 万条。车轴作为动车组关键承载部件，全寿命周期需承受载荷循环数高达5×109次。车轴的设计通常依据标准使用“无限寿命设计”理念进行，即车轴承受的工作应力应小于疲劳许用应力，以保证车轴在运行过程中不会发生疲劳失效。但车轴载荷循环周次已属于超高周范畴，其可能在应力幅值远小于107循环周次疲劳极限的情况下出现失效。在长期的线路运行过程中，车轴还可能会经受道砟击打、腐蚀环境等造成表面损伤，从而导致车轴的疲劳强度降低[1-4]。因此，基于“损伤容限”理念所制定的定期超声探伤和磁粉探伤应运而生，与“无限寿命设计”共同成为车轴安全性与可靠性的重要保障。

获得服役载荷、材料的裂纹扩展行为是开展车轴损伤容限分析的前提。JIN[5]确立了测力轮对制作方法，对轮对系统进行标定后，通过测试得到CRH6型列车的车轴应力谱；丁然等[6]对城际动车组轮轨力进行了研究，分析了速度级与线路对轮轨载荷的影响，得到4 600 km的轮轨力载荷谱，发现在同一线路的去程和返程中，垂向与横向轮轨力的分布也有明显不同；LUKE 等[7-8]使用M(T)试样进行了EA4T车轴材料的裂纹扩展试验，得到了EA4T车轴材料的裂纹扩展曲线，对比了不同应力比对裂纹扩展速率的影响，并在不同的加载次序下进行了裂纹扩展试验；POURHEIDAR 等[9]进行了全尺寸车轴裂纹扩展试验，并对比了不同裂纹扩展模型的准确性；SIMUNEK 等[10]使用SE(B)试样、1∶3车轴试样与1∶1车轴试样研究了裂纹扩展参数从小尺寸规模样本到实际规模组件的可传递性问题；GAO 等[11-14]通过仿真分析计算了含裂纹S38C 车轴的剩余寿命，同时使用空气炮模拟车轴击打伤影响，对S38C车轴疲劳强度与剩余寿命进行了研究；吴毅等[15]通过使用钨钢弹丸冲击EA4T材质车轴表面，研究了含异物击打伤动车组车轴的疲劳寿命，发现含1 mm深度击打伤缺陷的动力车轴在极端苛刻载荷条件下，仍然具有超过120万km的剩余寿命。因此，需要进行长周期跟踪测试，以明确在真实运营情况下车轴所经历的应力历程，并对影响因素进行分析。

本文作者使用智能轮对进行车轴动应力试验，建立实际运行状态下车轴关键截面的应力谱，确定车轴动应力影响因素，建立实际服役条件下的车轴台架试验谱，分别采用Paris 公式与NASGRO方程对车轴寿命进行预测，并通过全尺寸车轴裂纹扩展试验进行验证，为车轴产品研发和运用维护提供重要参考。

1 车轴线路动应力测试方法

随着我国动车组开行范围、里程、数量的增多、运营速度的提升和运用工况复杂程度的增大，获得实际运用条件下的车轴动应力是进行车轴结构可靠性分析和安全评估的重要基础。

采用时速为350 km/h的高速动车组智能轮对，在京沪线开展动力车轴动应力在线测试。图1所示为智能轮对示意图。智能轮对测试系统具有连续测量、实时处理、远程传输、无损测试、小巧轻便等特点，满足动车组车轴长期线路跟踪测试的需要。该系统主要包括DC/AC 逆变器、感应式电源头、感应线圈、遥测模块、应变片桥路、PC 模块、GPS 天线等。整套系统以PC 机为中心，使用DC/AC逆变器为感应式电源头进行供电形成磁场。通过车轴在旋转过程中带动感应线圈切割磁感线为测试系统供电，并将信号传输至PC 机进行处理，通过天线将测试数据传输至终端，在终端下载接收测试结果。

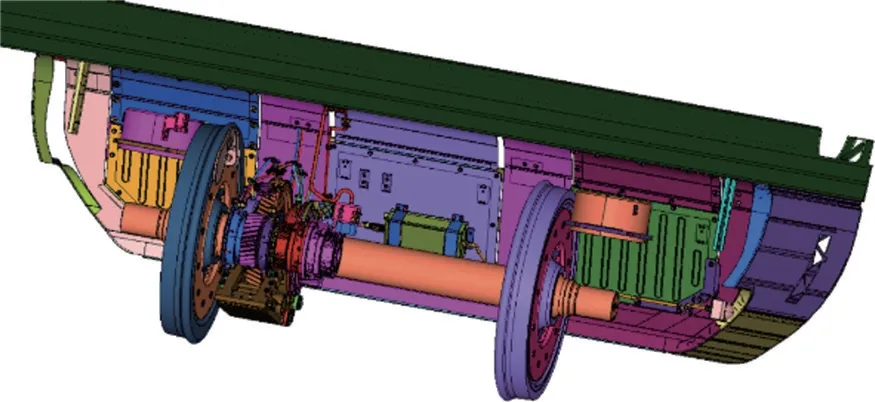
图1 智能轮对示意图Fig.1 Schematic diagram of intelligent wheelset

依据EN 13103—2017 标准对车轴进行应力计算，获得车轴高应力截面，即测点布置截面。图2所示为车轴截面测点的位置。由图2可见：S1测点在车轴轮座内侧截面(非齿轮箱侧)，S2测点在齿轮箱座内侧截面，S3测点在卸荷槽根部截面。

图2 车轴截面测点的位置Fig.2 Measuring point sections of axle

2 台架试验谱确定方法

如何编制既能反映车轴实际应力状态又能避免周期过长的台架试验谱是开展全尺寸车轴裂纹扩展寿命试验的关键。

高应力循环幅值对车轴剩余寿命计算具有较大影响，而有限里程的测试数据并不能反映其在全寿命运行过程中所经历的应力，因此，需要对车轴应力谱进行外推。对于高频次低应力区段的部分，可直接进行线性外推；对于应力极值的拟合外推需要着重关注，本文应用第二极值理论(又称Pickands-Ballkema-de Haan 定理)对车轴测试应力谱进行外推。该定理认为随机变量的超限分布函数Fu(s)必收敛到广义帕累托分布Gξ,β(s)，因此，可使用广义帕累托分布拟合极值区域概率密度函数，将有限测试里程的车轴应力谱外推至预期运行里程下的应力谱[16-17]，即

式中：u为极值区域与非极值区域的分界值；s为应力；sup为上确界，即最小上界；ξ和β为广义帕累托分布Gξ,β(s)的参数。

使用外推得到的车轴应力谱在进行台架试验时，由于外推应力谱总频次与分级数目较多，因此，不能直接用于台架试验，需要对车轴外推应力谱进行简化，得到适用于台架试验的台架试验谱。

图3所示为当卸荷槽截面存在裂纹时，在外推应力谱下裂纹前缘最深处应力强度因子变化图，其中应力频次为某应力水平在测试过程中出现的次数。结合文献[18]中所使用的方法提出适用于台架试验谱构建的“Omit”准则，即对一定深度与形貌的裂纹进行计算，确定出该裂纹前缘的强度因子，考虑到保守的试验结果，加载高于裂纹扩展门槛值的应力，并随裂纹深度的增大逐步调整需要加载的应力。

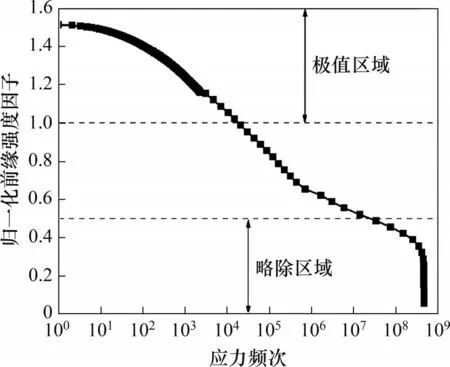
图3 不同应力频次下裂纹前缘强度因子变化Fig.3 Crack front stress intensity factor changes with different stress levels

3 裂纹扩展寿命计算方法

建立动车组车轴有限元模型，车轴材质为EA4T 钢。表1[19]和表2[7-8,19]所示分别为其力学性能与断裂力学参数，表2 中，C和m为材料参数，Kth为扩展门槛值。图4 所示为车轴加载与约束方式示意，F为加载的力。由图4可见：计算模型的约束、载荷与台架试验一致。即在车轮处施加全约束，在车轴另一端轴颈处施加载荷，以模拟台架试验中车轴的受载方式。

图4 车轴加载与约束方式Fig.4 Loading and restraint modes of axle

表1 EA4T材料力学性能参数[19]Table 1 Mechanical performance parameters of EA4T[19]

表2 EA4T材料断裂力学参数[7-8,19]Table 2 Fracture mechanics parameters of EA4T[7-8,19]

建立卸荷槽区域裂纹子模型，计算裂纹前缘的应力强度因子及裂纹的扩展情况，图5所示为裂纹子模型。通过子模型裂纹尖端应力场与位移场确定裂纹前缘各节点的扩展方向，结合裂纹扩展速率曲线计算各节点的扩展距离，计算并绘制出裂纹前缘各点在扩展后所处的位置，拟合得到新的裂纹前缘；最后，对扩展后的新裂纹前缘进行平滑处理，建立新的裂纹子模型。按照此方法不断迭代进行计算，直至完成目标循环次数或达到目标裂纹深度为止。

图5 裂纹子模型Fig.5 Crack sub-model

采用式(2)和式(3)2 种裂纹扩展模型计算裂纹扩展寿命：

式中：a为裂纹长度；N为交变载荷的周次；为裂纹扩展速率；C′，m′，p和q均为材料参数；R为应力比；ΔK为应力强度因子变化量；Kmax为最大应力强度因子；KC为断裂韧度。

可见，Paris 公式中裂纹扩展门槛值仅为判断是否扩展的阈值，NASGRO 方程则将裂纹扩展门槛值与断裂韧性均考虑在扩展速率的计算模型中。

4 台架试验方法

研究全尺寸车轴裂纹扩展试验方法，开展全尺寸车轴裂纹扩展寿命试验，验证车轴寿命预测模型的同时，可为车轴超声探伤周期优化提供参考。

进行裂纹扩展试验时首先要进行疲劳裂纹预制。本文作者采用预制人工缺陷，通过试验台加载在人工缺陷处萌生疲劳裂纹并控制其尺寸，使其达到试验要求。因此，应当在保证可萌生出疲劳裂纹的前提下，尽可能将人工缺陷的深度控制在较浅的范围内。使用电火花加工方式在车轴卸荷槽截面A处预制初始深度1.5～2.0 mm 的半圆形人工缺陷，并对人工缺陷进行复形，确定缺陷的真实形貌(图6(a))；将车轴与车轮进行装配，在车轴疲劳试验台上从高到低逐级施加150～200 MPa的应力，当车轴表面裂纹达到一定长度后，停止加载，得到用于车轴台架试验的初始疲劳裂纹(图6(b))。

采用立式车轴疲劳试验台(图6(c))加载车轴台架试验谱，进行车轴裂纹扩展寿命试验。试验加载频率与半轮对系统共振频率相关，本试验加载频率为15 Hz，试验温度控制为室温(20 ℃)。

图6 车轴疲劳试验方法Fig.6 Fatigue test method of axle

5 结果分析与讨论

5.1 车轴动应力线路测试结果

5.1.1 动应力与速度的关系

对比列车运行速度为唯一变量的300 km/h 与350 km/h 速度下的应力谱，如图7 所示。由图7 可见：在不同速度下，车轴动应力幅值在低应力、高频次区域差异较小，但在高应力、低频次区域存在明显差异；列车运行速度提高后，350 km/h速度级下的应力极值比300 km/h 速度级下的应力极值高约10%，这主要是因为车轴动应力幅值在低应力、高频次区域主要与轴重相关，因此，在不同运行速度级下差异较小；而速度的提升会在一定程度上增加轮轨作用力，尤其是过道岔、轨缝的冲击[20]，因此，会引起高应力、低频次区域车轴动应力幅值增大。

图7 不同速度下的车轴应力谱Fig.7 Axle stress spectra at different speeds

使用文献[21]中EA4T 材质全尺寸车轴S-N曲线并结合Miner 法则，计算此应力谱下的等效应力：

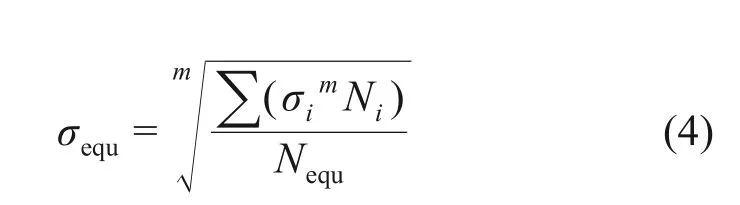
式中，σequ为等效应力；Nequ为等效应力对应的循环次数，此处取107次；σi为应力谱中各级应力幅值；Ni为应力谱中各级应力幅值对应的循环次数；m为S-N曲线参数，EA4T材质车轴m为9.2[21]。经计算可得，350 km/h 速度级下车轴等效应力为300 km/h速度级下的1.02倍。

5.1.2 动应力与线路的关系

选取京沪线上下行运行线路的测试数据，运行速度均为300 km/h时的应力谱对比结果如图8所示。由图8可见：上行时，车轴各截面应力谱应力极值与等效应力比下行的值均高约7%。这主要是因为当列车处于上、下行运行线路时，测试轴分别处于导向轴与非导向轴状态，当测试轴为导向轴状态时，其轮轨作用力会比非导向轴状态的作用力高，因此，在上下行不同运行线路时，车轴应力谱应力极值与等效应力均有较大差别。

图8 不同运行线路下的车轴应力谱Fig.8 Axle stress spectra on different operating tracks

5.1.3 动应力与运行里程的关系

图9所示为不同跟踪里程下的车轴应力谱。由图9可见：随测试里程增长，车轴最高频次应力无明显变化，而应力极值逐渐增大，但增长速率逐渐减缓，30 万km 与40 万km 的应力极值已基本一致。

图9 不同运行里程下的车轴应力谱Fig.9 Axle stress spectra at different operating mileages

5.2 台架试验谱确定

图10 所示为采用极值理论将10 万km 车轴测试应力谱外推至40 万km 的结果，图中一并列出40万km测试应力谱。由图10可见：40万km外推应力谱与其测试应力谱具有较高的重合度，外推应力谱应力极值比测试应力谱应力极值高约0.68%，极值理论用于车轴应力谱极值外推具有良好的效果。

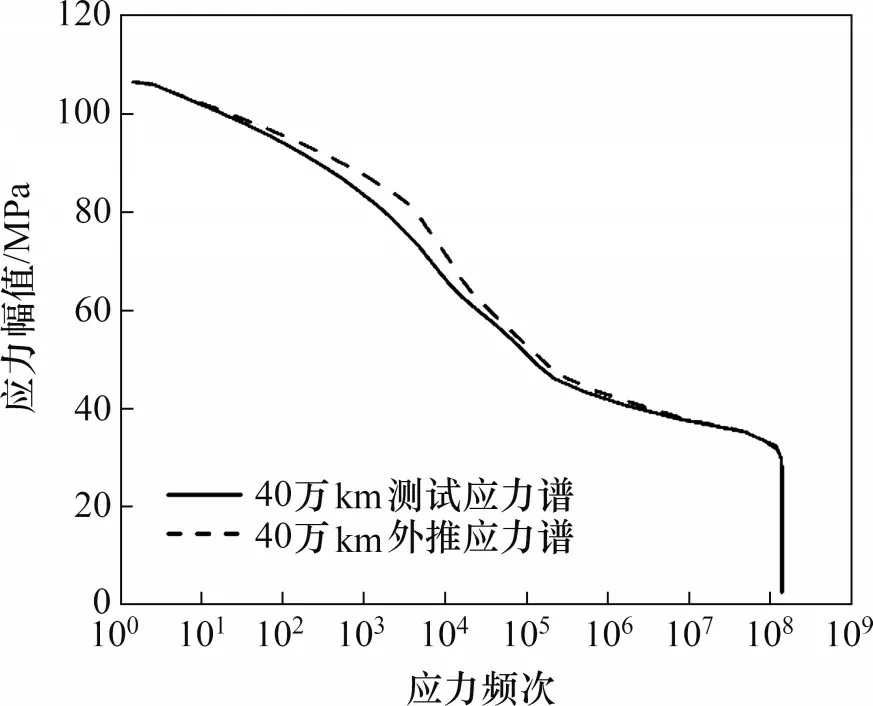
图10 车轴外推应力谱与测试应力谱的对比Fig.10 Comparison of axle extrapolated stress spectrum with test stress spectrum

使用极值理论对车轴应力谱进行外推，分别得到列车运行140 万km 与1 500 万km 时卸荷槽截面的应力谱。图11 所示为外推到不同里程时车轴应力谱。由图11 可见：140 万km 外推应力谱的应力极值约为121 MPa，1 500万km外推应力谱的应力极值约为127 MPa。

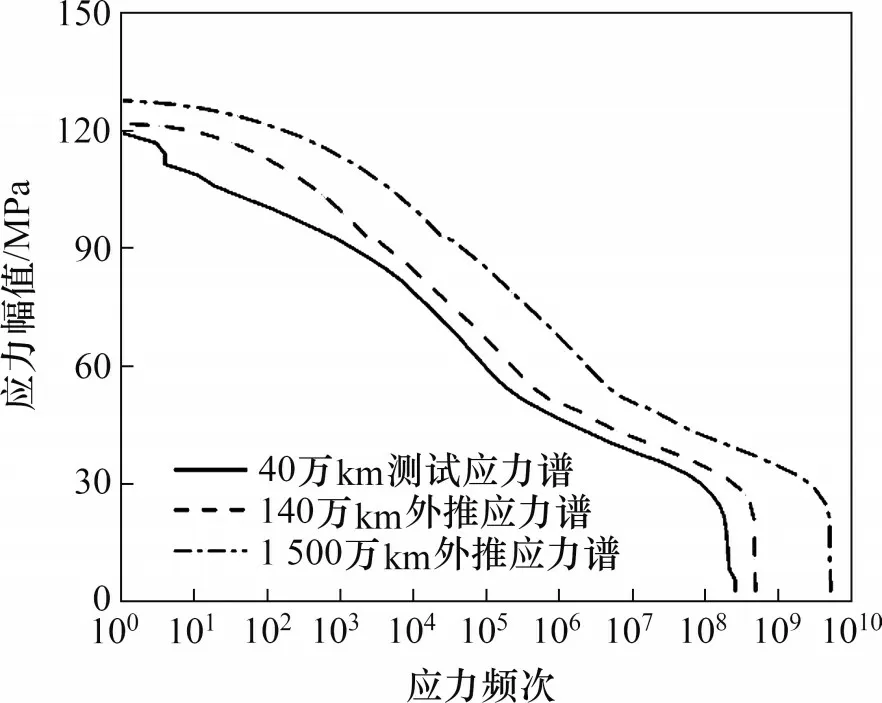
图11 车轴外推应力谱Fig.11 Extrapolated stress spectra of axle

裂纹前缘应力强度因子与车轴所承载的应力水平呈线性关系。当卸荷槽存在初始深度为7 mm的裂纹时，在140 万km 外推应力谱下，计算裂纹前缘应力强度因子，根据其计算结果，划分应力谱，如图12所示。EA4T车轴材料裂纹扩展门槛值为13 MPa·m1/2，将低于门槛值一半以下的应力循环舍去，并将剩余的应力水平分为4级，且每级应力水平取该级中的最大值，以获得相对保守的试验结果。同时，考虑运用中可能出现的车轮多边形磨耗[22-28]所带来的轮轨垂向力增加以及高、低载荷加载次序的影响，将各级应力放大1.2倍，并划分为7个谱块，最终得到台架试验谱。

图12 车轴试验谱应力区域划分Fig.12 Stress area division of axle bench test spectrum

图13 所示为台架试验谱加载谱块图。由图13可见：最高级应力水平为144.0 MPa，位于应力谱中的极值区域；最低级应力水平为64.8 MPa，表征低幅值高循环次数应力区域所带来的影响；中间2级应力水平为过渡应力级。

图13 台架试验加载谱块图Fig.13 Loading block diagram of bench test

5.3 车轴裂纹扩展寿命预测结果

分别使用Paris 公式与NASGRO 方程计算140 万km 台架试验谱下含初始裂纹深度为7.0 mm的半椭圆形裂纹车轴的扩展寿命(裂纹位置见图6(b))，图14所示为使用2种裂纹扩展速率曲线模型的计算结果。由图14可见：采用Paris公式计算的裂纹深度扩展至9.1 mm，采用NASGRO 方程计算的裂纹深度扩展至7.7 mm；由深度7.0 mm 扩展至9.1 mm时，NASGRO方程的计算寿命为380万km，为Paris公式计算寿命的2.7倍。

图14 Paris公式与NASGRO方程计算结果对比Fig.14 Comparison of calculation results between Paris formula and NASGRO equation

5.4 车轴裂纹扩展寿命台架试验结果

采用图13 所示的台架试验谱对含裂纹车轴进行疲劳加载。在试验过程中，实时监控裂纹的扩展，140 万km 应力谱加载后停止试验，对裂纹所在区域取样进行观测。图15 所示为裂纹面观测结果。由图15可见：加载140万km应力谱后，车轴疲劳裂纹深度由初始7.0 mm扩展至7.5 mm。

图15 裂纹面观测结果Fig.15 Observation results of crack surface

图16 与表3 所示为仿真分析结果与试验结果对比。由图16 与表3 可见：采用Paris 公式得到的裂纹深度扩展量为试验结果的4.2 倍，采用NASGRO 方程得到的裂纹深度扩展量为试验结果的1.4 倍。对比深度由7.0 mm 扩展至7.5 mm 时的运行里程，Paris 公式计算结果为试验结果的26.1%，NASGRO 方程计算结果为试验结果的76.5%。由此可见，在进行车轴剩余寿命预测时，2 种裂纹扩展速率模型的预测结果均较保守，且NASGRO方程更接近于实际情况。

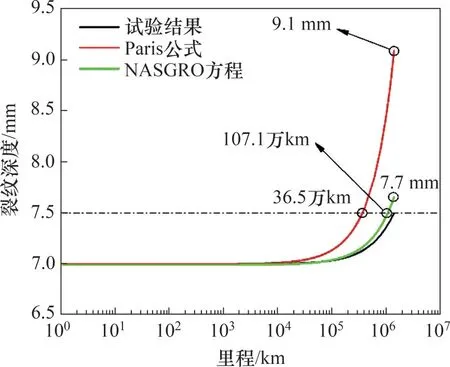
图16 仿真结果与试验结果对比Fig.16 Comparison of simulation results and bench test results

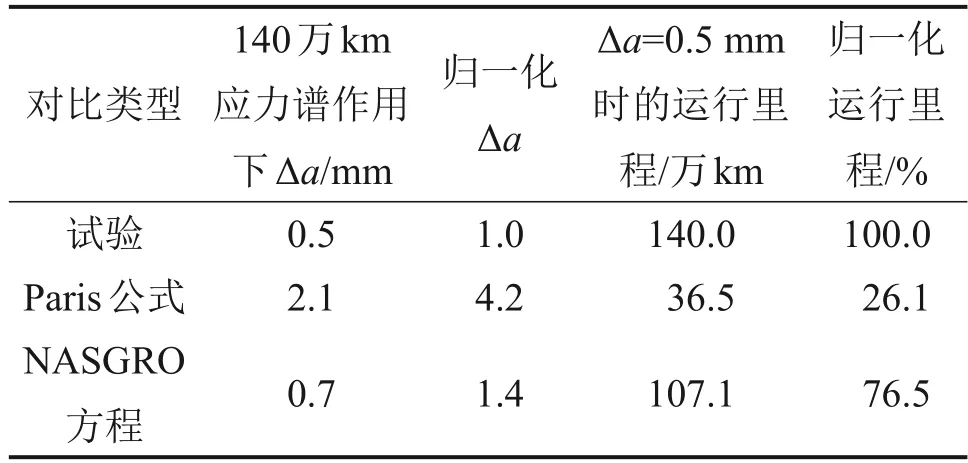
表3 仿真结果与试验结果Table 3 Simulation results and bench test results

6 结论

1)运行线路、运行速度、车轮状态等均会对车轴应力产生影响。在不同线路下，车轴应力谱极值与等效应力有约7%的波动；350 km/h速度级下的应力极值为300 km/h速度级的1.1倍，等效应力为300 km/h速度级的1.02倍。

2)基于车轴动应力长期线路测试数据，使用极值理论对应力谱进行外推，获得140 万km 的外推车轴应力谱，并提出了一种适用于评价车轴超声探伤间隔的试验台架谱构建方法。

3)在140 万km 应力谱加载下，开展了全尺寸车轴台架裂纹扩展寿命试验。当初始深度为7.0 mm的疲劳裂纹扩展至7.5 mm时，NASGRO方程计算结果是裂纹深度由7.0 mm 扩展至7.7 mm，相比于Paris公式更准确，且具有一定的安全裕度。