基于宏微观耦合深度学习的高速铁路无砟轨道板表面裂缝精细化测量

胡文博，王卫东，汪雯娟，彭俊，吴铮，王劲，邱实

(1.中南大学土木工程学院，湖南长沙，410075；2.中南大学轨道交通基础设施智能监控研究中心，湖南长沙，410075；3.中南大学重载铁路工程结构教育部重点实验室，湖南长沙，410075；4.首都经济贸易大学工商管理学院，北京，100026)

高速铁路在运营阶段，受气候、环境、服役时间等影响，无砟轨道板表面逐步出现裂缝并不断生长。裂缝持续增长，会导致无砟轨道结构失效，严重威胁高速铁路的运行安全[1-3]。精准测量无砟轨道板表面裂缝宽度是评估轨道板服役状态劣化程度的重要手段，也是养护维修决策的关键依据[4]。

由于高速铁路线路长、服役条件复杂、表面裂缝的可识别性差，在天窗点的人工巡道难以高效、精准识别裂缝并判断其宽度，漏检或错检不可避免。目前，人们研发了不少高精度的机器视觉巡检设备[5-7]和基于图像的裂缝识别技术，替代人工巡检和人工裂缝识别，其中，裂缝宽度自动化测量的前提是裂缝边界的判识[8-9]，所以，裂缝边界的判识精度直接影响裂缝宽度测量的准确性。现有裂缝边界判识的图像处理技术可以分为边缘检测[10]、阈值分割[11]、区域增长[12]、分水岭分割[13]和滤波器[14]，这些技术通过处理巡检图像中的浅层特征(如颜色、灰度、轮廓、边缘和频率)来区分裂缝像素和背景像素[15]。尽管它们结构简单且计算成本较低，但最佳阈值和种子像素的选择需要大量的先验知识和工程经验[16-19]，若裂缝特征或检测背景发生较大变化，则需要调整计算参数甚至重新设计算法。因此，这些算法具有高特异性、低泛化性和不确定性，易产生模糊或不连续的裂缝边界(漏检)，从而导致测量的宽度无效[20]。近年来，以深度语义分割网络为代表的深度学习方法直接利用巡检图像的像素信息作为输入，通过多层卷积运算对图像特征进行自动提取和高层抽象，最大限度地挖掘输入图像的所有有效特征信息，从而实现对裂缝像素和背景像素的精准区分，克服了传统图像处理技术的不足[21-22]。YANG等[23]提出了一种深度全卷积神经网络，所得裂缝宽度像素的判识精度超过97%，相对测量误差在20%以下。JI等[24]提出了一种基于深度语义分割网络(DeepLabv3+)和快速并行细化算法(FPT)的融合算法，能够精准识别沥青或混凝土路面裂缝像素，且所得相对测量误差比中轴算法等传统方法的低。然而，现有的深度语义分割网络的应用场景大多单调、均一[25]，其共性在于仅通过微观边界层面的分析来判识裂缝边界，难以有效区分裂缝像素以及与裂缝高度相似的噪声、污损等背景像素，对复杂背景状况的适应性差造成漏检或误检，导致裂缝宽度的测量结果与实际严重偏离[26]。为解决跨复杂背景的无砟轨道板裂缝精细化测量难题，本文在总结现有方法局限性的基础上，提出一种基于宏微观(宏观区域层面、微观边界层面和裂缝几何特征层面)耦合的深度学习算法。

1 基于宏微观耦合的深度学习算法

1.1 基本框架

通过宏观区域—微观边界—几何特征3个层面的裂缝特征提取和处理结果传递，构建裂缝区域提取—裂缝边界判识—裂缝宽度测量的精细化算法，形成无砟轨道板巡检图像—裂缝边界—裂缝宽度的映射关系。该算法的基本框架如图1所示。

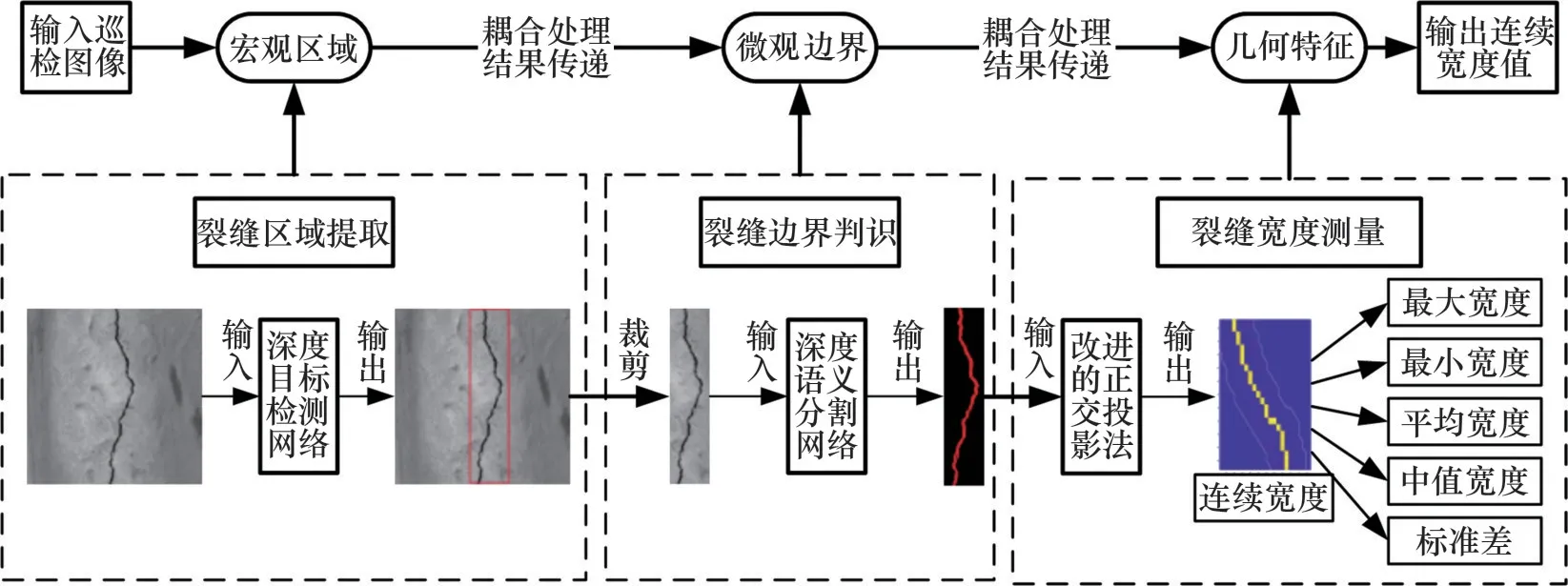
图1 基于宏微观耦合的深度学习算法的总体框架Fig.1 Total architecture of deep learning algorithm based on multi-scale coupling

1.2 宏观区域层面的裂缝区域提取

宏观区域层面的裂缝区域提取能够减少大量非目标区域的噪声、污损等背景像素，并降低后续微观边界层面的裂缝边界判识的计算成本。采用YOLOv3 深度目标检测网络通过输出边界框从巡检图像中快速、高效地提取裂缝所在区域。YOLOv3是一种典型的单阶段目标检测网络，它将区域分类和坐标回归封装到1个网络中，目标在边界框中的置信度和目标所属类别的概率在1次评估中直接从完整图像中捕获，从而实现实时、高效的端到端检测。图2所示为本文所使用的YOLOv3的网络主干架构，其最显著的特点是具有宏微观的检测能力，对裂缝这种微小目标的定位精度高。

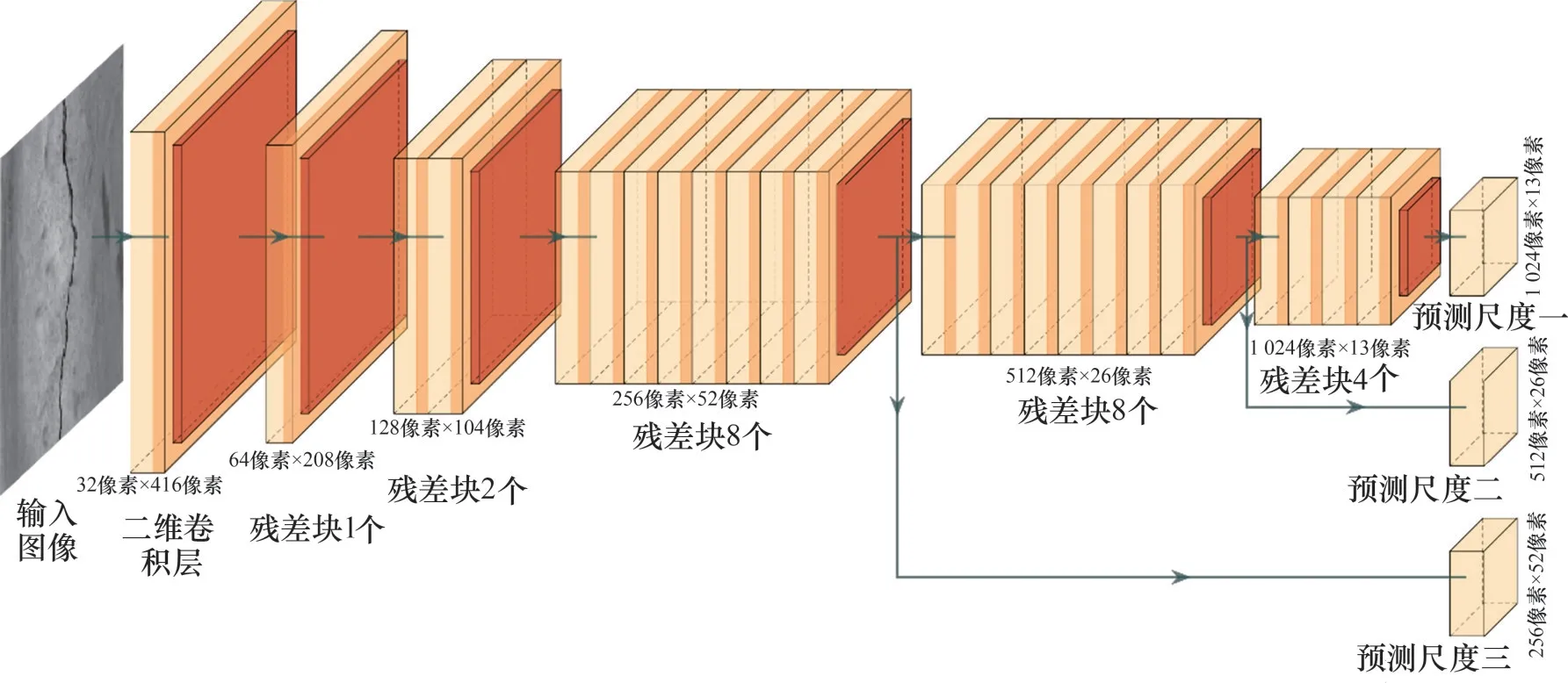
图2 YOLOv3深度目标检测网络的主干架构Fig.2 Backbone architecture of YOLOv3 deep object detection network

1.3 微观边界层面的裂缝边界精准判识

根据输出的边界框坐标对宏观区域层面的裂缝区域提取结果进行裁剪，并将裁剪后的裂缝区域作为DeepLabv3+深度语义分割网络的输入，以逐像素地判识裂缝边界。DeepLabv3+是一种用于语义分割的编码器-解码器架构，如图3 所示。在编码器模块(Encoder)中，首先，采用ResNet-101模块(主干网络)快速捕捉裂缝边界的有效特征信息，并使用空洞卷积模块在不改变特征图像素的同时调整感受野以提取宏微观的语义信息。然后，通过多孔空间金字塔池化模块对捕捉到的裂缝特征信息进行筛选并得到最具辨别力的信息。最后，将提取到的最具辨别力的整个图像的特征图输入到解码器模块(Decoder)中。解码器模块通过上采样操作对输入的特征图进行解码，并与来自ResNet-101模块的相应低级特征进行融合后还原到与输入图像一致的空间尺寸，从而实现对裂缝区域中的裂缝边界像素的精准判识。

图3 DeepLabv3+深度语义分割网络的总体架构Fig.3 Overall architecture of DeepLabv3+deep semantic segmentation network

1.4 几何特征层面的裂缝精细化测量

QIU等[27]提出正交投影法，采用Canny边缘算子获取裂缝边界进行宽度计算。然而，Canny边缘算子对含噪图像的判识效果差，输出的模糊或不连续的裂缝边界会导致裂缝宽度测量结果严重偏离实际。为此，本文提出一种改进的正交投影法，采用微观边界层面的裂缝边界判识方法代替原始的Canny算子，并根据输出的裂缝边界判识结果提取单像素的裂缝骨架和轮廓线，计算裂缝的连续宽度。首先，将裂缝骨架的方向定义为由局部相邻骨架点导出的每个骨架点处的切线方向。然后，沿着逆时针方向和八邻域对裂缝边界像素进行跟踪匹配，通过匹配所有的边界像素，将二值边界转换为1 个分层序列，从而得到2 条裂缝轮廓线。最后，从每个骨架点像素引出正交投影射线作为骨架的法线，每条正交投影射线和裂缝的2条轮廓线有2个交点，这2个交点之间的欧几里得距离被定义为裂缝内部某点的连续宽度(见式(1))，如图4所示。根据裂缝连续宽度的分布计算最小值、最大值、平均值(见式(2))、中值(见式(3))和标准差(见式(4))，以精细表征裂缝的宽度。

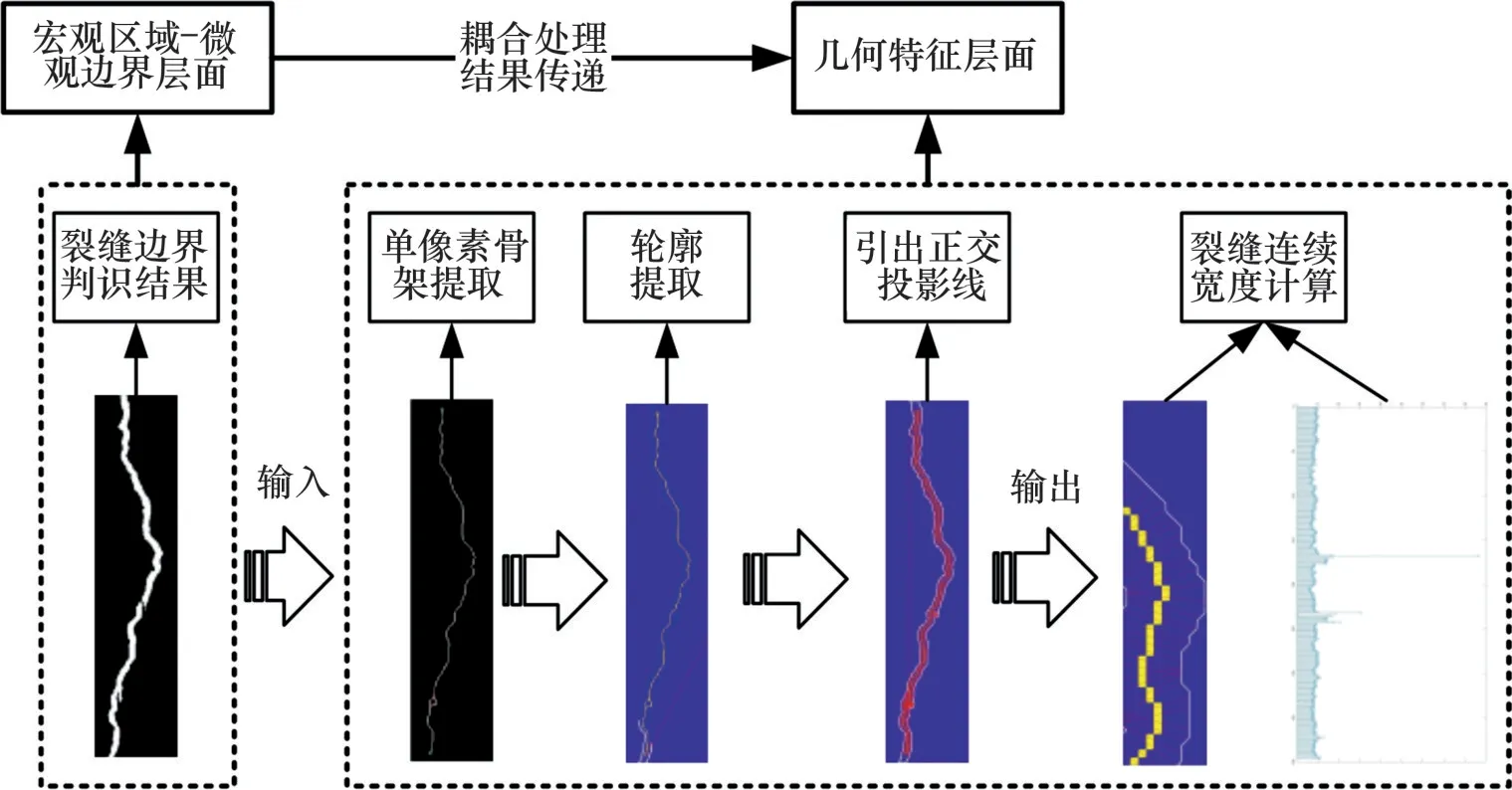
图4 改进的正交投影法的计算流程Fig.4 Computational processes of the improved orthogonal projection method

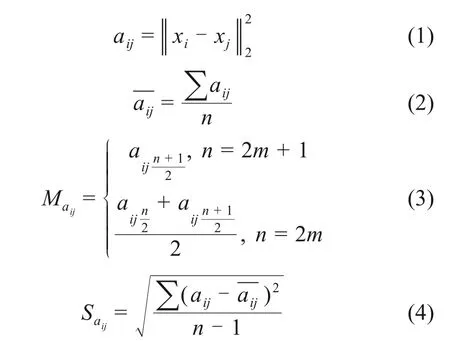
式中：aij为裂缝中某一点的连续宽度；为奇数点集中某点的连续宽度；为偶数点集中某点的连续宽度；xi和xj分别为裂缝轮廓线和正交投影射线的交点横坐标和纵坐标；n为裂缝连续宽度测量点集；m为任意自然数；ˉaij为裂缝连续宽度的平均值；Maij为裂缝连续宽度的中值；Saij为裂缝连续宽度分布的标准差。

2 案例分析与算法实现

2.1 数据采集与标注

通过安装在高速综合轨道巡检车上的高分辨率线阵相机对某高速铁路区段CRTSⅢ型无砟轨道板进行扫描，获得4 096 像素×4 096 像素的原始轨道板巡检图像。利用规格为60 kg/m的钢轨轨头的实际宽度(73 mm)作为参照，得到采集区域对应的实际长×宽为235.5 mm×235.5 mm。此外，由于高速铁路轨道结构一般处于自然环境中，受自然光照和相机光源的叠加影响以及巡检车自身振动和噪声等复杂环境条件的干扰，采集到的巡检图像存在噪声、污损等复杂、不规则背景。

为了降低计算机显存的需求，所采集的图像被进一步裁剪为400 像素×400 像素的图像子块，并从中随机选取50张图像作为验证集，450张图像作为训练集。其中，每张图像均对应1 张标签图(ground truth)。标签图是人工通过labelme 软件对图像中的裂缝进行标注得到的训练参考图。首先采用矩形框对裂缝所在区域进行标注得到深度目标检测网络的训练参考图，在此区域内，沿着裂缝边界逐像素地标注裂缝轮廓得到深度语义分割网络的训练参考图，如图5所示。

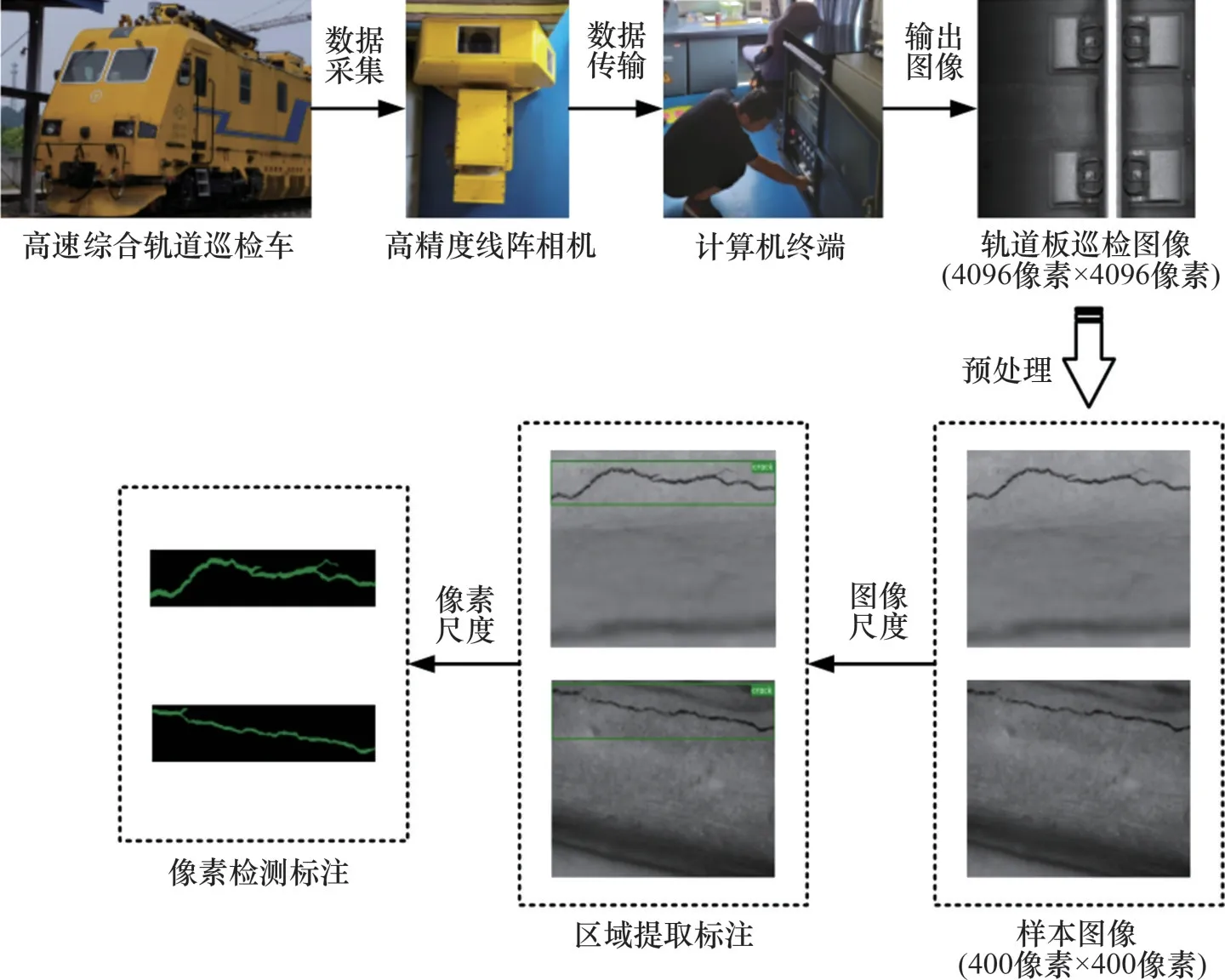
图5 无砟轨道板裂缝图像数据采集与标注Fig.5 Data acquisition and annotation of crack images for ballastless track slab

2.2 实验设置

本文设置2个损失函数分别对宏观区域层面和微观边界层面的误差进行评估，并校正YOLOv3深度目标检测网络和DeepLabv3+深度语义分割网络的检测性能。在裂缝区域提取阶段，预测框面积和标注框面积的平方误差之和被定义为YOLOv3的损失函数(见式(5))，以校正预测边界框坐标和置信度。

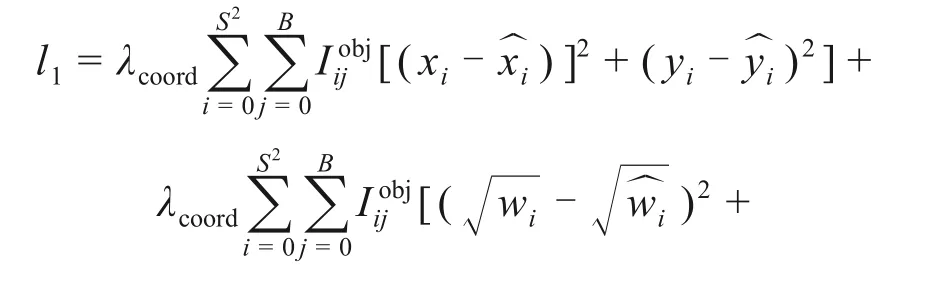
在裂缝边界像素判识阶段，采用交叉熵损失评估预测像素和标记像素之间的误差(见式(6))，以评估DeepLabv3+的裂缝边界判识效果。

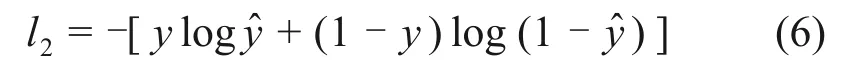
式中：l2为DeepLabv3+的总损失；y为标签值；为预测值。

此外，本文设置10 折交叉验证以获得具有更丰富图像特征的训练集和验证集，即每次随机地选取500张样本图像中的10%作为验证集，剩余的作为训练集，这样可以得到10组＜训练集，验证集＞。使用这10 组＜训练集，验证集＞充分训练YOLOv3深度目标检测网络和DeepLabv3+深度语义分割网络，最大程度上消除由于有限、单一的数据特征导致的宏观区域层面、微观边界层面和几何特征层面之间的检测误差积累。本文以GPU 为计算核心(CPU 为AMD2990WX@3.0 GHz，RAM 为64 GB，GPU 为NVIDIA GeForce RTX 2080Ti)，依托Facebook 开源的深度学习框架PyTorch1.2.0，通过10 折交叉验证的充分训练得到的最优超参数设置如表1所示。

表1 实验超参数设置Table 1 Setting of experimental hyperparameters

2.3 评价指标

本文采用所有类别检测对象的平均精度(mean average precision，MAP)来衡量YOLOv3 网络的检测性能。MAP的计算关键在于预测区域和标注区域之间的重叠程度U(见式(7))：

式中：A为预测区域面积；B为标注区域面积。

U的阈值通常设置为0.5，当预测边界框和标注边界框之间的U大于此阈值时，该预测边界框被定义为阳性样本，否则为阴性样本。此外，预测边界框的置信度阈值也被用于区分正预测和负预测。当预测结果的U大于0.5且预测正确时，表示裂缝边界判识的真阳性结果(TP)；当预测结果的U小于0.5 或预测错误时，表示裂缝边界判识的假阳性结果(FP)；当不存在标注框时，表示裂缝边界判识的假阴性结果(FN)，这表明模型无法从人工注释中检测到任何对象标签。

基于这些指标可以确定精准率(P)和召回率(R)。精准率表示正确检测的目标占检测总数的比例(见式(8))，召回率表示正确检测的目标占实际目标总数的比例(见式(9))。通过计算不同的置信度阈值下YOLOv3网络在测试集上的精准率和召回率，得到P-R曲线。MAP通过对P-R曲线进行积分得到，表示P-R曲线与坐标轴围成的面积。

采用不同类别检测对象的U的平均值(MU)度量预测的裂缝像素和标记的裂缝像素之间的重叠程度(见式(10))，以评估DeepLabv3+深度语义分割网络的裂缝边界判识效果。

式中：n1为检测对象的类别数量。

2.4 实验结果

图6 和图7 所示分别为针对450 张训练集图像和50 张验证集图像的裂缝区域提取和裂缝边界判识的实验结果，分别经过近1 000 个轮次和500 个轮次的充分训练，YOLOv3 网络和DeepLabv3+网络的损失值、MAP和MU均收敛，此时，这2个网络都达到了拟合状态。通过计算验证集P-R曲线与2个坐标轴围成区域的面积，得到YOLOv3 网络的MAP为93.36%，尤其当预测边界框的置信度阈值达到0.9时，该网络的精准率仍在80%以上，显示出优异的裂缝区域识别性能。通过统计50 张验证集图像上U的平均值，得到DeepLabv3+网络的MU为82.99%。

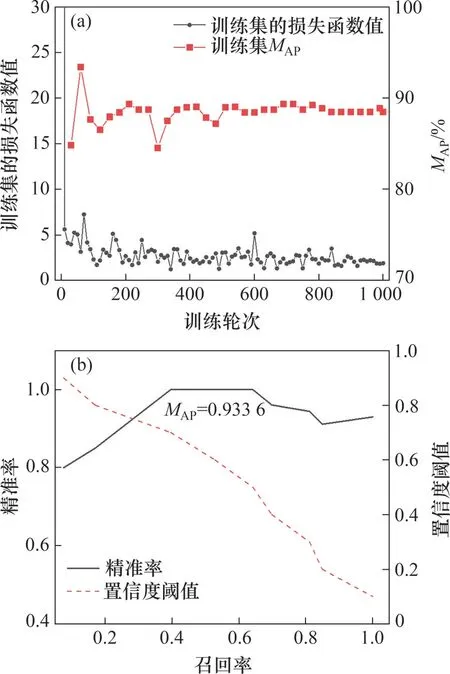
图6 YOLOv3深度目标检测网络的训练结果Fig.6 Training results of YOLOv3 deep object detection network

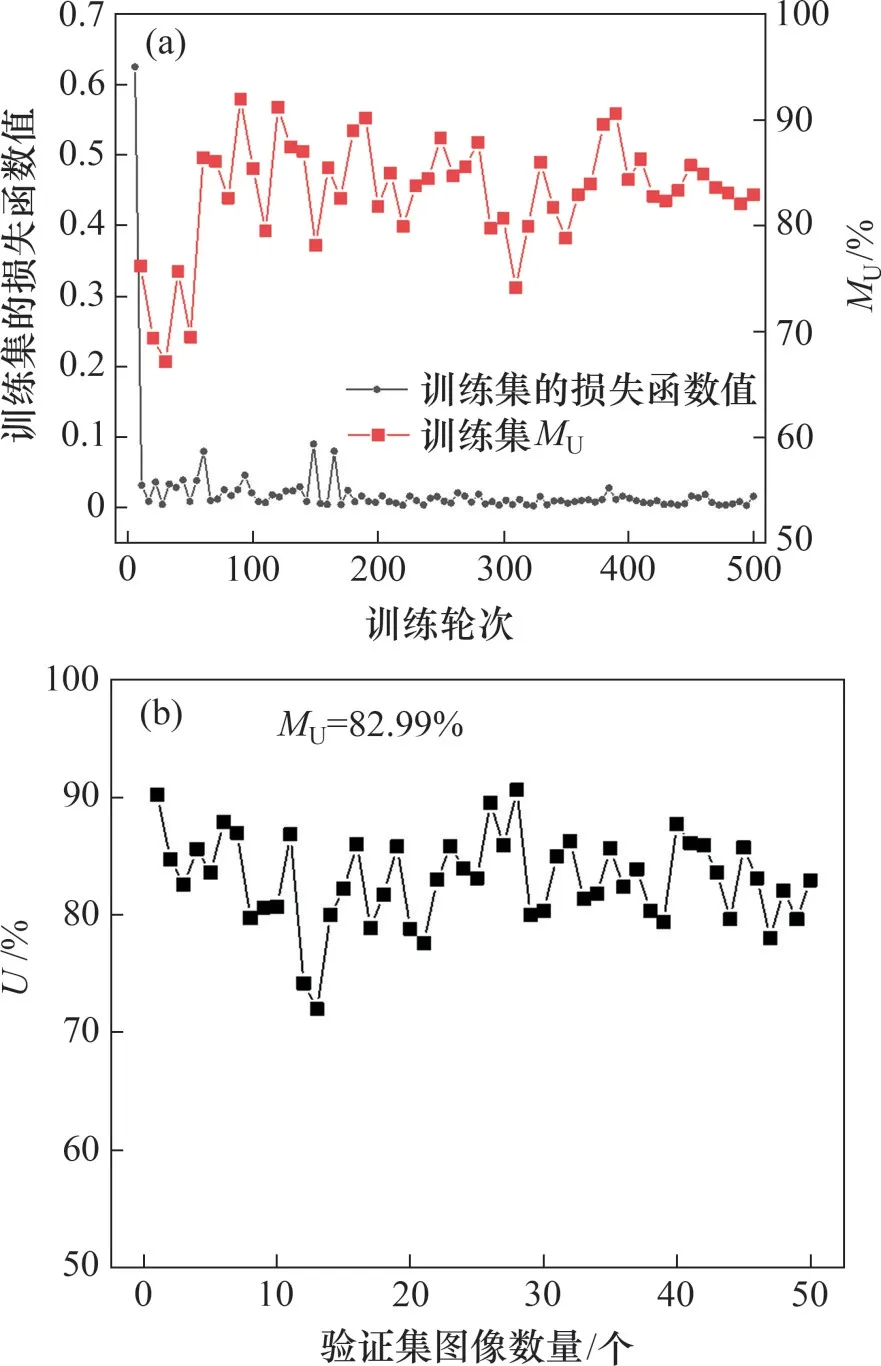
图7 DeepLabv3+深度语义分割网络的训练结果Fig.7 Training results of DeepLabv3+deep semantic segmentation network

3 结果对比与评估

3.1 宏微观耦合算法与单一微观边界层面的深度学习算法的对比

图8所示为本算法与现有2种微观边界层面的深度语义分割网络对于30 张测试集图像的裂缝边界判识结果，其中U-Net 网络的计算时间(单张图像处理时间)最低，但测试集的MU仅为68.8%，而DeepLabv3+网络的MU达77.59%，但计算时间较高。宏微观耦合算法用于宏观区域-微观边界层面耦合分析时的总计算时间由2部分构成：裂缝区域提取的计算时间(A区域)和裂缝边界判识的计算时间(B 区域)。尽管宏微观耦合算法消耗的总计算时间略高于单一微观边界层面的DeepLabv3+网络的计算时间，但其MU相比单一微观边界层面的DeepLabv3+网络的MU提高了近7%，且宏观区域层面的裂缝区域预提取也使得该算法在微观边界层面判识裂缝边界时的计算时间比DeepLabv3+的低。

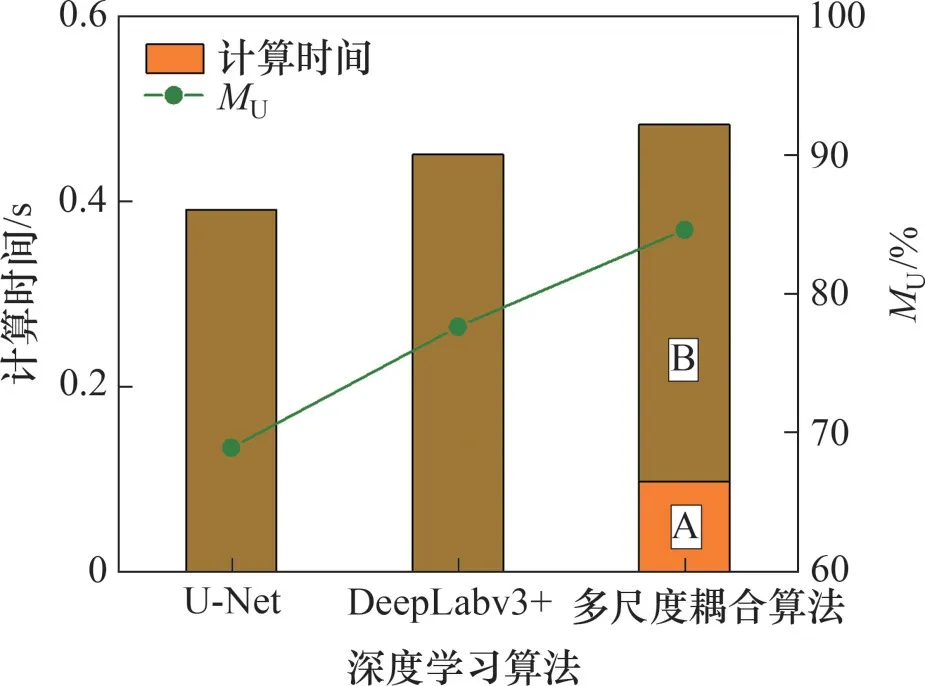
图8 不同深度学习算法在测试集上的裂缝边界判识结果Fig.8 Results of crack boundary detection by different deep learning algorithms on testing set

不同算法对于4张测试样本图像的裂缝边界判识结果见图9。U-Net 网络对于裂缝细节的判识效果不佳，容易产生不连续的裂缝边界，且U-Net和DeepLabv3+均易将噪声、污损等与裂缝高度相似的背景像素误判为裂缝像素(图9中黄色圆圈所示)。与U-Net 和DeepLabv3+相比，宏微观耦合算法在宏观区域层面提取裂缝区域时有效地消除了目标区域之外的噪声、污损的干扰，对经过坐标裁剪后的裂缝区域进行微观边界层面的边界分割能够得到更精细化的判识结果。但测试样本3的判识结果显示宏微观耦合算法难以完全去除复杂背景条件下的干扰，存在于裂缝区域之内的噪声、污损仍会对该算法得出的微观边界层面判识结果造成不利影响。

图9 不同深度学习算法对于4张测试图像的裂缝边界判识结果Fig.9 Results of crack boundary detection by different deep learning algorithms for four tested images

3.2 宏微观耦合算法与传统正交投影法的对比

为了进一步测试本算法的裂缝宽度测量性能，将本算法和传统正交投影法针对4张测试样本图像计算得到的裂缝宽度表征指标(最小宽度、最大宽度、平均宽度、中值宽度和标准差)进行对比，结果见图10。图10(a)中直方图为传统正交投影法的计算结果，点线图为宏微观耦合算法的计算结果。由传统正交投影法计算得到的测试样本1和测试样本2 的最大宽度均是宏微观耦合算法计算结果的8倍以上，且远大于其平均宽度测量值，说明传统正交投影法易将噪声、污损等与裂缝高度相似的复杂背景误判为裂缝像素，引起骨架变形，从而导致最大宽度测量值出现较大偏差。进一步地，采用宏微观耦合算法可以得到4张测试样本中裂缝的最小宽度，而采用传统正交投影法计算得到的裂缝的最小宽度近似为0 mm。这是由于传统正交投影法在裂缝像素轮廓提取阶段采用的Canny算子容易产生不连续的裂缝边界，难以获得裂缝真实的最小宽度。此外，宏微观耦合算法计算得到的4张测试样本的裂缝平均宽度和中值宽度的差值均小于0.1 mm，而采用传统正交投影法时，该差值可能达到0.3 mm。图10(b)所示为2 种方法测得的裂缝的连续宽度的标准差，其中宏微观耦合算法的裂缝连续宽度测量结果的标准差均在2 mm 以下，而传统正交投影法在测试样本2上的标准差达18 mm，显示出宏微观耦合算法具有更加优异的测量稳定性和可靠性。上述对比结果表明宏微观耦合算法能够在噪声、污损等复杂背景状况的干扰下更精细、更稳定地表征裂缝宽度。

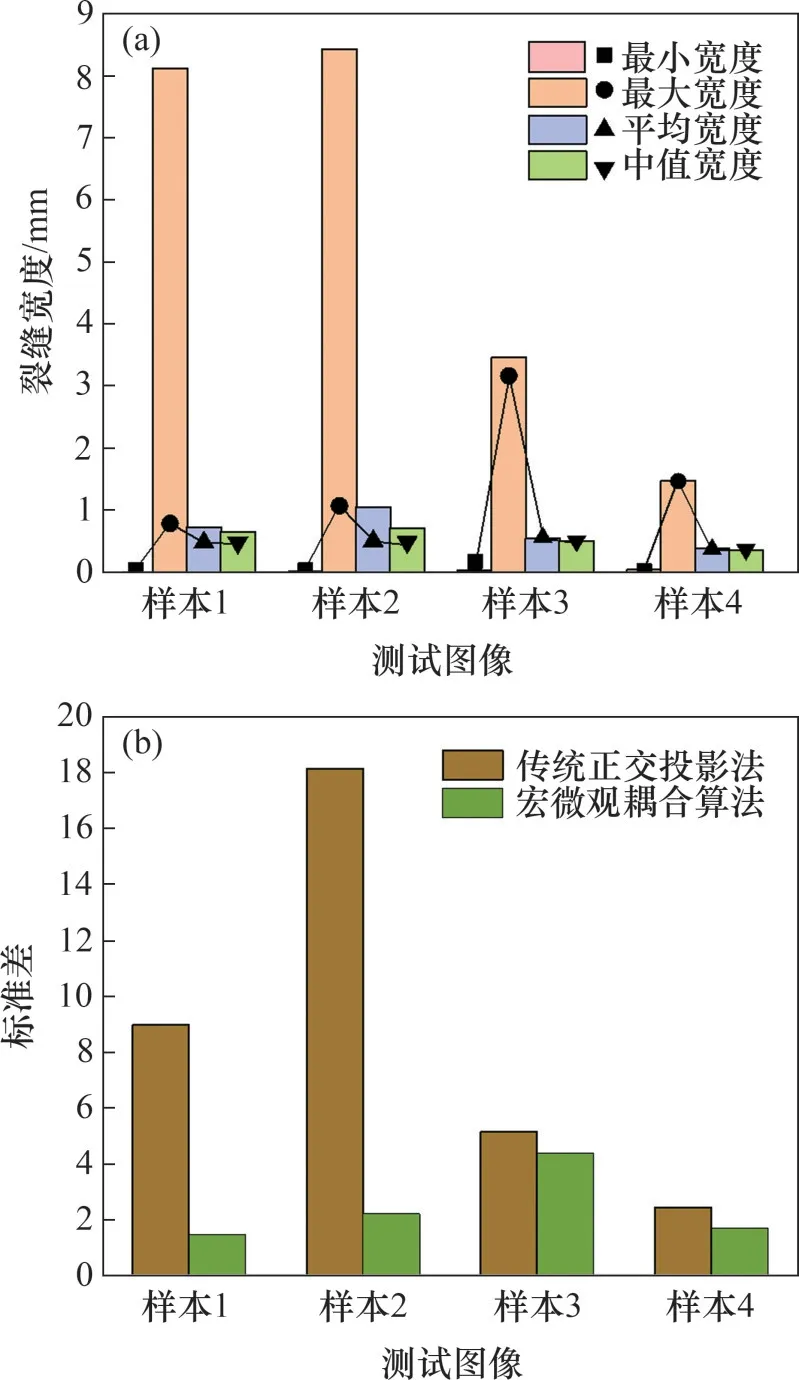
图10 宏微观耦合算法和传统正交投影法的裂缝宽度测量结果对比Fig.10 Comparison of crack width measurement by macro-micro coupling algorithm and by traditional orthogonal projection method

4 结论

1)提出了一种基于深度学习的包含裂缝区域提取、裂缝边界判识和裂缝宽度测量的宏微观耦合算法，其在宏观区域层面实施的裂缝区域预提取能够去除大部分的噪声、污损导致的像素误判，显示出对与裂缝高度相似的复杂背景条件的良好适应性。

2)尽管宏微观耦合算法在图像-微观边界层面耦合分析时的总计算时间(单张图像处理时间)比DeepLabv3+网络的略高(多0.03 s)，但其在30张测试集图像上的裂缝边界判识精度达84.57%，相比单一微观边界层面的深度语义分割网络的(U-Net和DeepLabv3+)判识精度最高提升近15%。

3)宏微观耦合算法能够消除噪声、污损的干扰，从而得到更精细化的裂缝宽度，且其计算得到的裂缝连续宽度波动(标准差)远比传统的正交投影法(降幅最高达90%)的低，显示出该算法的裂缝宽度测量性能具有精度高、稳定性强和可靠性好等特点。