一种适用于北极双轴声道的改进压缩匹配场定位算法研究
吕玉娇 刘崇磊 张扬帆 黄海宁*
①(中国科学院声学研究所 北京 100190)
②(中国科学院先进水下信息技术重点实验室 北京 100190)
③(中国科学院大学 北京 100190)
1 引言
北极因海冰覆盖、暖流流入等而具有特殊的信道形式,表面声道处声波与冰层下表面碰撞剧烈,传播损失大,次表面声道因远离冰层,传播损失小,在如此复杂信道情况下如何提高声源定位的准确性是一个重要的研究问题。匹配场处理(Matched-Field Processing, MFP)[1]作为一种与声波传播特性相结合的定位方法[2,3],可以利用声场模型来很好地模拟水下环境中信号的收发过程,将真实声场与通过模型计算求得的拷贝场按照一定的匹配准则进行计算,其匹配原理与波束形成原理相似,被称为广义波束形成。匹配场方法中应用最为广泛的是常规Bartlett线性匹配器[4,5],该方法将归一化的格林函数与接收信号在频域做相关后得到模糊平面,模糊平面的最大值所对应的位置即为估计的声源位置。此种方法计算简单稳定,不受信号快拍数限制,但它存在的问题是旁瓣能量较高,声源真实位置易淹没在匹配场模糊平面中。波束形成中最小方差波束形成器作为一种抑制旁瓣的有效方法,在匹配场中也有应用,最小方差匹配场处理[6,7]是一种可以提高目标分辨力的匹配场方法,旁瓣能量较Bartlett方法低,但方法涉及协方差矩阵的求逆操作,对计算的快拍数有一定要求,计算时间较久。贝叶斯学习方法[8,9]按照概率密度函数大小进行迭代,实现匹配场中声源位置参数的空间寻优,但须给定一定的迭代次数,计算复杂度较高。
压缩感知[10,11](Compressive Sensing, CS)方法作为信号处理领域的一大方向,对于提高信号分辨力有重要意义。而在匹配场中,声源个数远远小于网格点数,可以看成稀疏结构,因此压缩感知可以与匹配场处理方法结合来作为提高目标位置分辨力的一种方法,且压缩匹配场对快拍数等没有限制,也可以估计多个声源的位置[12]。2011年Mantzel等人[13]提出压缩匹配场的概念,并从单频和多频的角度对常规匹配场与压缩匹配场作了比较。Gemba等人[14,15]提出压缩感知与自适应处理器具有相似特点,通过对稀疏度加以限制提出了自适应压缩匹配场的方法。此类方法可以同时估计出声源位置与发射信号频谱值,但在匹配过程中,声源位置也易受到所估计的信号频谱的影响,一个参数的误差将引起另一个参数的误差,最终导致所估计的声源位置准确度受到影响。
在此之前,也有学者提出结合相位信息进行匹配的思路,文献[16]利用不同频率之间的差频相位信息对相干匹配场进行了优化,通过全局搜索差频,结果分辨力更高。文献[17]将相位下降搜索法运用到匹配相位的搜索中,计算简单。文献[18]将射线掠射角、深度组成的平面定义为一个简化相位平面,并分析了声速变化、声源深度变化对该平面产生的影响。文献[18]将“掠射角-深度”平面作为相位平面进行匹配,不需考虑多径带来的干扰影响。但上述方法均未考虑过利用阵元域相位信息进行匹配计算。
在计算拷贝场与测量场向量的匹配相关度的时候,测量场向量的准确与否直接关系到所估计声源的位置、发射信号频谱的精确度。而测量场向量受到发射信号频谱、信道传递函数、叠加噪声的影响,在使用压缩匹配场方法进行位置及频谱这两个未知参数的估计时,一个参数的误差必将导致另一个参数包含误差[15]。因此,为了提高复杂信道环境中对位置参数估计的准确度,该文从消除频谱参数对位置参数的影响这一角度出发,基于相位归一化原理提出从相位的角度对压缩匹配场算法加以一定优化,以提高匹配的稳健性,用于应对复杂信道情况。该方法首先将格林函数和接收信号频域向量进行相位归一化,再以归一化相位信息代替幅度信息进行匹配,不需要考虑发射信号频谱,在一定程度上减少了不确定因素的干扰,算法复杂度低,且不受快拍数限制。
2 压缩匹配场算法
CS理论[19]的提出解决了在不满足传统信号采样条件的情况下的数据存储与恢复问题,该方法主要针对稀疏信号,是在奈奎斯特采样原理的基础上进一步突破的方法。传统奈奎斯特采样原理表示,当信号采样率低于两倍的信号最高频率时,采样结果在频域不发生混叠,如此方能保留原始信号的信息,而CS方法提出,如果信号在某个域为稀疏信号,则可以通过远低于两倍信号最高频率的采样率进行采样。
在匹配场定位中,声源所在区域被划分成多个网格点,通过将实测数据与声源在不同网格点处所对应的仿真格林函数进行幅值匹配,可以实现对目标声源的位置估计。这里,声源的个数是远小于网格点数,因此可以从稀疏角度对匹配场定位进行求解。


3 改进压缩匹配场算法
根据相位归一化方法[20],由于接收信号的相位组成受到发射信号相位、信道传递函数相位、叠加噪声相位所产生的影响,通过多次不同测量来估计首阵元的信号相位,可以用于对其他阵元的相位进行相位归一化,以消除未知信号频谱及噪声对接收信号的相位影响。如果拷贝向量不对信号频谱进行处理,将无法与测量场更好地匹配,在匹配多个频点的数据时处理器性能将下降。这里将相位归一化方法用于压缩匹配场上,消除信号频谱在幅值和相位上的影响,只考虑噪声的影响,以提高压缩匹配场的定位准确度。


4 算法验证
4.1 算法仿真
如图1所示,使用KRAKEN建立仿真的水体环境,水深1019.45 m,声源频率为600 Hz,各层介质的上下界面声速值均已给出。取一个深度为120 m、水平距离为10 km的2维平面作为声源可能存在区域,将平面按照深度间隔1 m、水平间隔50 m进行网格点划分。计算每个网格点的格林函数,将其与接收信号的频域分量进行匹配。接收端为10元垂直线阵,阵元间隔10 m,距离水面最近的阵元深度为水下10 m。

图1 环境仿真模型
将改进方法与常规Bartlett方法、压缩匹配场方法进行单次定位结果比较,信噪比依次为0, 5,14 dB,快拍数为5,十字代表真实声源位置,圆形代表不同方法的估计位置。仿真结果表明,从旁瓣能量上比较,常规方法旁瓣高于其他两种方法,导致模糊平面精度较低;从定位结果准确度上来看,常规方法和改进方法均可估计出正确位置,而压缩匹配场方法结果则在深度和距离上存在一定误差。
通过Monte Carlo方法分别计算在0, 5, 14 dB信噪比下不同方法定位结果的统计误差,如图2-图4所示,重复次数为500次,将多次计算的距离和深度结果取平均后放入表1中。可以发现,随着信噪比增高,改进后方法比改进前的压缩匹配场方法的统计误差越来越低,估计准确度有所提高。

表1 统计误差

图2 信噪比为0 dB情况下定位结果比较
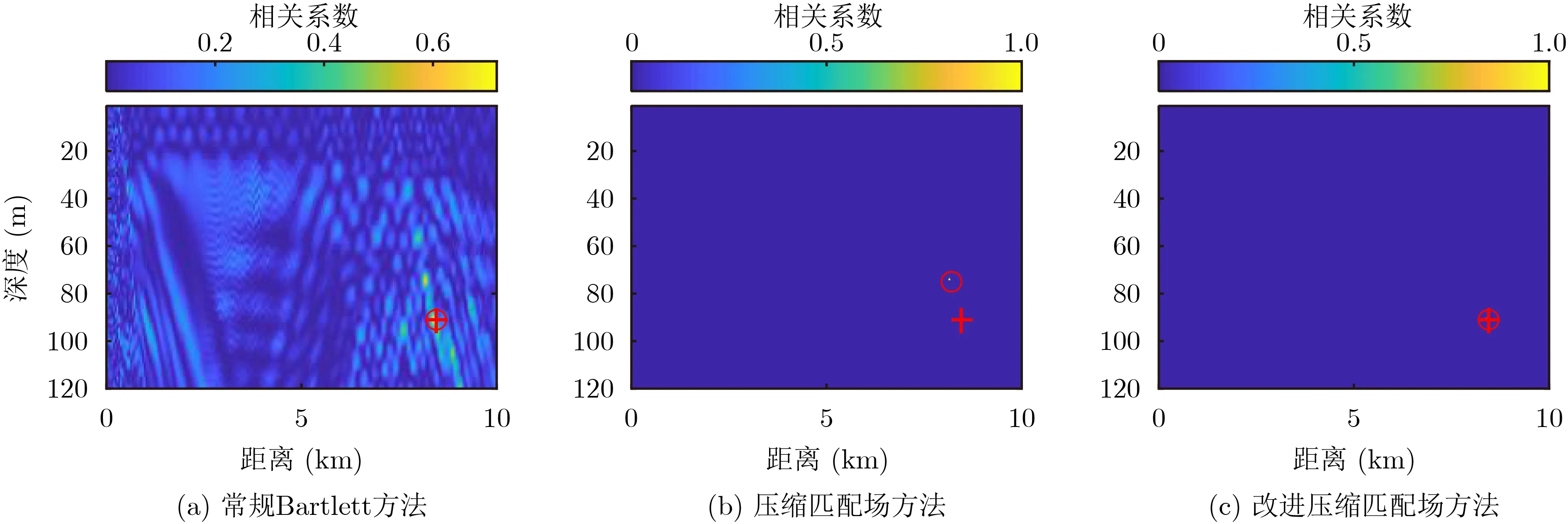
图3 信噪比为5 dB情况下定位结果比较
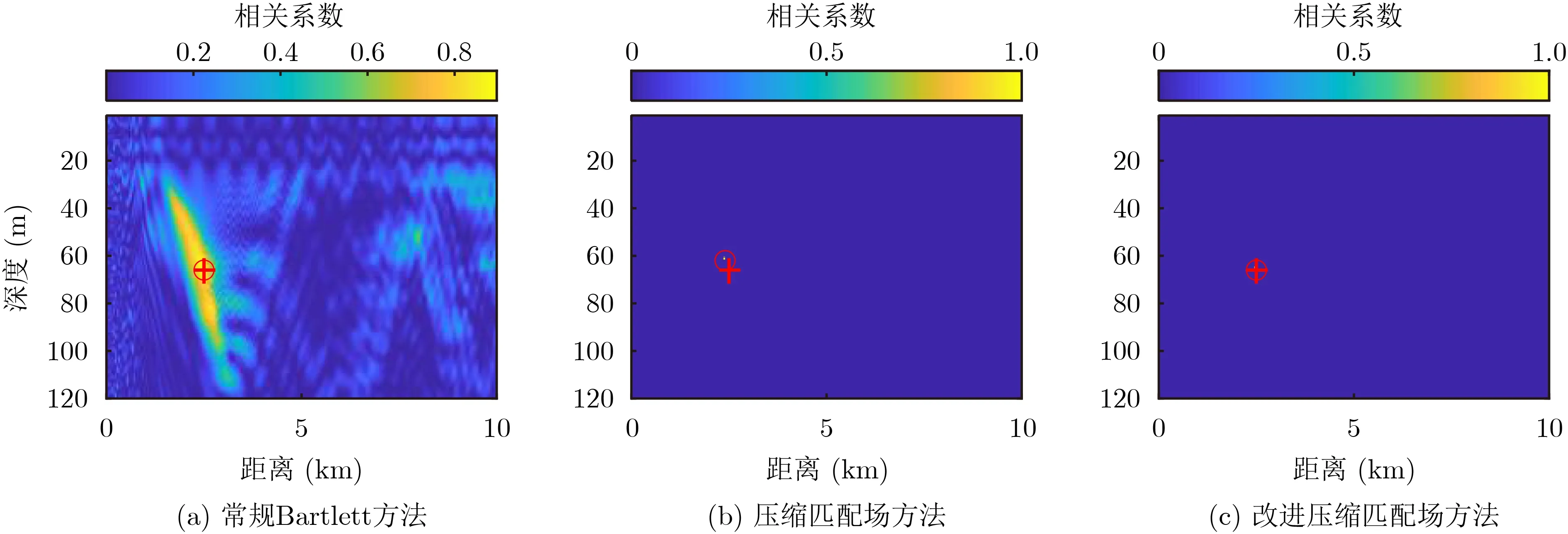
图4 信噪比为14 dB情况下定位结果比较
对于不同定位方法的估计结果,其定位准确率的定义如下:当估计深度与真实深度之间相差2 m,且估计距离与真实距离之间相差100 m时,视为定位准确,否则为定位不准确;若仿真总次数为N,定位准确的次数为Ntrue,则定位准确率Ptrue的计算方法如式(11)所示。
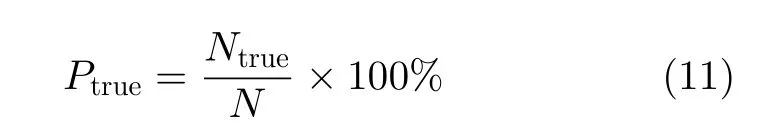
给定不同信噪比,分别进行1000次Monte Carlo仿真,改进前、后压缩匹配场方法的定位准确率结果如图5所示。从结果上可以看出,当信噪比高于5 dB时,改进压缩匹配场的定位准确率明显高于改进前方法,表明改进方法在一定情况下比改进前方法估计出准确结果的可能性更高。

图5 不同方法的定位准确度
4.2 性能分析


图6 不同假设下统计量的概率密度分布函数
将统计量与不同的检测门限进行比较,并绘制出改进压缩匹配场模型下的受试者工作特征曲线(Receiver Operating Characteristic, ROC),结果如图7所示。曲线表明,当虚警率低于0.1时,快拍数越高,检测概率越低;当虚警率高于0.1时,快拍数越高,检测概率越高。

图7 不同快拍下的ROC曲线
4.3 试验数据验证
4.3.1 数据介绍
选择中国第11次北极科学考察声学试验中加拿大海盆拉距试验的数据进行算法验证。试验中,拖曳声源入水50 m,以2.5 m/s的速度远离接收端,在拖曳过程中发射端发射多个线性调频信号,信号被接收端接收并记录。接收阵深度与声速剖面深度变化对比如图8所示,接收阵为15元均匀垂直线阵,各阵元间隔为10 m,其中距离空气-水界面最近的阵元深度为水下6 m。如图8所示,声速剖面类型为双轴声道声速剖面,受暖流影响,不同于北极典型的表面声道声速剖面,该类型声速剖面在深度为100 m左右出现声速局部极小值,由于声波在传播过程中会向声速小的方向弯折,因此在次表面声道轴深度上,声波传播损失小,可以传更远。图9分析了在上表面反射系数较小情况下的双轴声道环境传播损失,可以看出在次表面声道深度上传播的声波不易受上表面影响,沿声道轴以较低的传播损失向外传播。
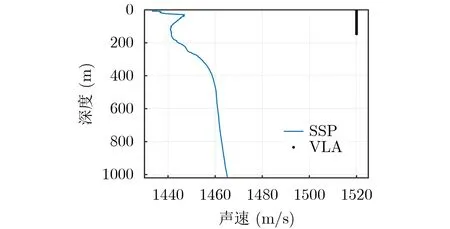
图8 试验环境声速剖面
4.3.2 仿真模型建立
根据试验环境建立匹配场仿真模型,由于试验过程中拖曳船无法测量底部环境信息,因此将水体环境设置成表2所示的单层水体介质加沉积层的模糊模型。环境模型总深度为1019.45 m,声速剖面由声速剖面仪测量,为北极典型双轴声道声速剖面,次表面声道轴位于水下100 m左右。选定感兴趣区域作为搜索区域,假设声源可能深度在0~120 m范围内,可能距离在0~10 km范围内,深度间隔为1 m,距离间隔为50 m。

表2 参数设置
4.3.3 数据处理结果
发射信号为占空比1:10的线性调频信号,频段为600~800 Hz,接收端采样频率为10 kHz。如图10所示为其中第5个阵元前2 min内接收信号的时频图。可以看出,信号源每分钟内发射一段6 s长的线性调频(Linear Frequency Modulation,LFM)信号,且接收信号质量较好,未淹没在船只航行过程中产生的低频线谱中。定位仪(Global Positioning System, GPS)记录的声源与接收阵之间的距离变化如图11所示。
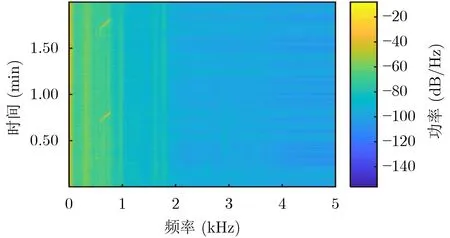
图10 接收信号时频图

图11 声源距离随时间变化情况
为了提高定位的准确率,选择多频点进行匹配场处理。取9:01对应的接收数据,进行600~700 Hz带宽内频点的不同方法的处理,此时声源距接收阵约4 km。将多个频点的模糊平面计算结果进行平均后,结果如图12所示,同时记录每个频点的位置估计结果,同样进行平均后以红色圆圈的形式将估计值标注到图12上,具体估计值如表3所示。从结果上可以看出,改进方法比改进前在距离及深度估计结果上均具有更小的误差,与常规方法相比,旁瓣低,结果分辨率更高。

表3 估计结果比较
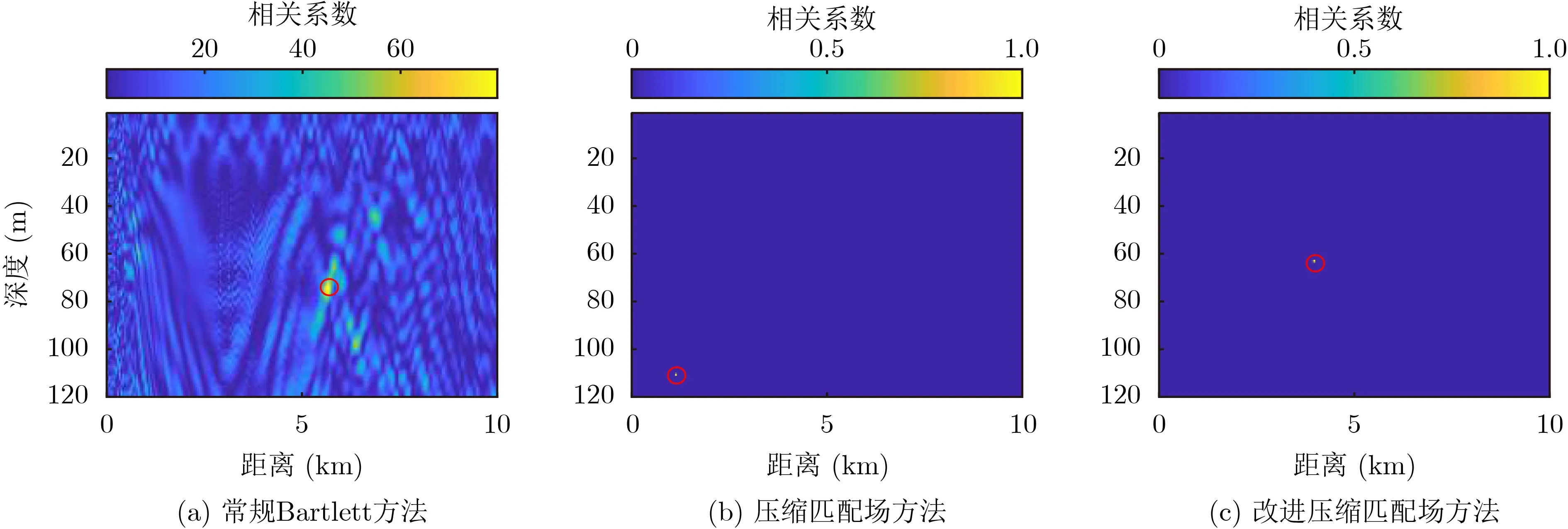
图12 不同方法的多频点处理结果
分析未改进的压缩匹配场定位方法结果误差较大的原因,可能是由于环境失配导致建立的环境模型中拷贝场与真实信道传递函数之间的偏差较大,不适合使用幅值来进行匹配,而改进后的压缩匹配场方法则在一定程度上克服了这一困难,将估计结果的误差进一步缩小,提高了估计的准确度。
5 结束语
常规匹配场方法旁瓣较高,分辨力低,压缩感知作为一种在传统采样原理上有所突破的新技术,与匹配场结合后提高了常规方法的分辨力,减少了旁瓣对目标位置的干扰。为了提高压缩匹配场方法在声源位置估计上的准确度,本文提出了一种改进的压缩匹配场定位方法,利用阵元域的归一化相位、幅值信息进行仿真场与测量场的匹配,使得估计结果不受到发射信号频谱的影响,将测量场视为仅被噪声污染的向量进行匹配。经试验数据处理发现,改进后方法与改进前在深度估计的误差问题上有很大改善,且比常规匹配场方法具有更低的旁瓣,在常规方法表现不佳时,该方法仍能维持较稳健的性能,可以很好地估计目标的深度。但算法未考虑声源位置不在网格点上的情况,网格的精细度在一定程度上影响了估计结果的准确度,因此在后续工作中,将针对这一问题进行自适应栅格化问题的研究。

