基于多层双向长短时记忆网络的水声多载波通信索引检测方法
朱雨男 解方彤 张明亮 王 彪 葛慧林
(江苏科技大学电子信息学院 镇江 212100)
1 引言
水声信道的复杂多径和时变空变特性对实现稳健的高速率水声通信提出了巨大挑战。以正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)[1]为代表的水声多载波调制技术频带利用率高且能有效抵抗频率选择性衰落,其诸多的衍生调制方式如正交信号分割复用[2]、滤波器组多载波(Filter Bank MultiCarrier, FBMC)[3,4]、索引调制OFDM[5,6]等均已成为水声通信领域的研究热点。
索引调制技术最初用于多输入多输出系统对空域中的激活天线进行选择,文献[7]将其应用到频域来控制激活的子载波位置,增加了活跃子载波间的稀疏性,进一步降低了频率偏移带来的影响。文献[8]将索引调制与FBMC联合(Index Modulated FBMC, FBMC-IM),一方面充分利用了原型滤波器组优良的时频聚焦特性来减少带外辐射、抵抗符号间干扰和载波间干扰,另一方面静默子载波的存在也削弱了FBMC系统中时频格点1阶邻域内的固有虚部干扰。但由于发送端将部分数据比特作为索引比特来激活子载波,FBMC-IM系统在均衡后需对活跃子载波的位置进行检测,在恢复信号时引起误码的形式包括子载波星座符号映射错误和活跃子载波位置检测错误。针对后者,目前常用能量检测(Energy Detection, ED)、最大似然(Maximum Likelihood, ML)和对数似然比(Log-Likelihood Ratio, LLR)算法进行检测[5]。ML检测对所有可能出现的子载波位置映射组合进行穷举;LLR检测通过计算最大后验概率来进行判别,后验概率的值越大则被看作活跃子载波的可能性越大。近年来随着大数据和人工智能技术的发展,神经网络广泛用于调制识别[9]、信道建模[10]和信号恢复[11,12]等,其不需要严格定义的模型就可以处理模糊信息或逼近非线性曲线,在信号处理领域具有很好的应用前景。文献[10]将条件生成对抗网络引入自编码网络通信系统中模拟信道所带来的影响,连接了发送端的编码网络和接收端的译码网络,实现端到端的智能通信。文献[11]将卷积神经网络引入水声多载波通信接收端实现信道估计和信号检测,相比传统的最小二乘估计和基于全连接网络的接收机,深度模型具有更好的特征提取效率和系统误码率性能。文献[12]通过两个级联的子网络将信道估计和均衡过程加入到样本数据预处理中,相比前者“强解调”式的直接输出所预测的发送比特,提升了深度学习方法的可解释性。
将深度学习应用到水声通信系统的理念刚刚起步[13],针对索引调制中的活跃子载波位置检测问题,本文提出一种基于双向长短时记忆网络(Bidirectional Long Short-Term Memory, BLSTM)的水声FBMC-IM索引检测器,自动获取活跃子载波位置信息特征,采用数据驱动的方式判定系统子载波的活跃状态,提高检测精度。将均衡后的分组载波序列作为特征向量,利用one-hot编码思想设计该组对应的标签向量,送入BLSTM网络进行离线学习和在线检测。
2 水声FBMC-IM通信系统
2.1 系统模型


图1 FBMC-IM系统发送端框图

2.2 检测算法


3 基于BLSTM的索引检测
3.1 网络模型



图2 BLSTM结构图

3.2 索引检测器构建
与ML算法相似,均衡后的数据yg一方面经过BLSTM检测活跃子载波位置,另一方面通过符号译码器计算出星座比特误码率。以(K,L)=(4,2)为例,共有6种活跃子载波组合可供选择,若选用其中组合C1~C4,索引调制的映射关系如表1所示,经one-hot编码后形成 1 ×4的标签矩阵。图3所示网络结构由多个BLSTM隐藏层、1个全连接输出层级联而成,输出层采用softmax激活函数,输出结果是一个4维的概率阵。将yg与对应的one-hot标签作为一组输入输出数据来训练BLSTM网络,通过反向传播算法不断减小输出值与标签值之间的误差。本文中采用多分类问题下的交叉熵损失函数来衡量网络输出与真实标签间的误差

表1 ( K,L)=(4,2)索引调制映射表

图3 基于多层BLSTM的索引检测框图

当损失值随着迭代训练的进行达到预设阈值或一定轮次后损失值不再减小时,网络离线学习完成。各神经元和LSTM单元所产生的参数都保存在网络模型中,在FBMC-IM接收端在线索引检测时直接输出预测结果,进一步通过译码恢复出索引比特。
3.3 复杂度分析
对于第g组子载波块,本文所提索引检测器与传统检测算法的复杂度对比如表2所示。ML检测的复杂度与Ig和sg的实现种类成正比,与p1和L呈指数倍增长。ED检测和LLR检测分别对比K个子载波上的最大符号能量和最大后验概率,大大降低了检测复杂度。基于BLSTM的方法将索引检测任务看作 2p1元分类识别,计算量主要集中在网络迭代训练过程中,在网络测试阶段直接输出识别结果,相较于子载波块整体估计的ML检测复杂度也有明显的提升,相较于ED检测和LLR检测在计算中不会出现未曾选用的活跃子载波组合情况,系统误码率也更低。

表2 索引检测算法复杂度对比
4 仿真分析

FBMC-IM系统的误码存在两种形式:当索引位置检测正确时,由于干扰和噪声导致的星座比特错误;当索引位置检测错误时,存在索引比特检测错误和因此导致的星座比特错误。本文采用类似信号识别的概念来进行FBMC-IM活跃子载波索引检测,表3所示各信噪比下的BLSTM检测与传统检测算法的误索引率(Index Error Ratio, IER)对比,结果表明LLR的逐子载波计算后验概率与ED的IER相近,BLSTM在低信噪比时由于样本带噪严重,无法有效学习到数据的特征,但在高信噪比下对整组载波进行识别的速度和准确率均有提升,且随着活跃子载波数量的增加效果越明显。
图4所示以 (K,L)=(4,1)为例,本文所提索引检测算法在不同接收信噪比下的误码率性能,此时传输的索引比特和符号比特占比相等。仿真结果表明在VTRM均衡后,LLR检测和ED检测的两种形式误码都较为严重,相比之下BLSTM检测直接大幅降低了索引比特出错,抑制了第2种形式的误码,间接地提升了符号比特的性能,整体的系统误码率优于传统索引调制检测算法的任一误码形式。

图4 基于BLSTM索引检测的FBMC-IM系统误码率性能
图5对比了3种子载波占空比下的FBMC-IM系统误码率,此时系统以不同的频谱效率作为代价来增加每个载波块中静默子载波数量,降低子载波间干扰,稳步提升了系统的误码率性能。仿真结果表明BLSTM检测在各个模式下的表现均优于传统方法,且随着静默子载波数量的增加,性能提升的效果越明显,与表3的IER值相互对应,对于索引模式的切换具有较高的鲁棒性。同时可以发现在(K,L)=(4,3) ,(K,L)=(4,2)时采用BLSTM索引检测算法取得了传统算法在 (K,L)=(4,2) ,(K,L)=(4,1)时的误码率性能,在同等条件下本文方法可以有效提高水声FBMC-IM通信系统的频谱效率,提高信息传输速度。
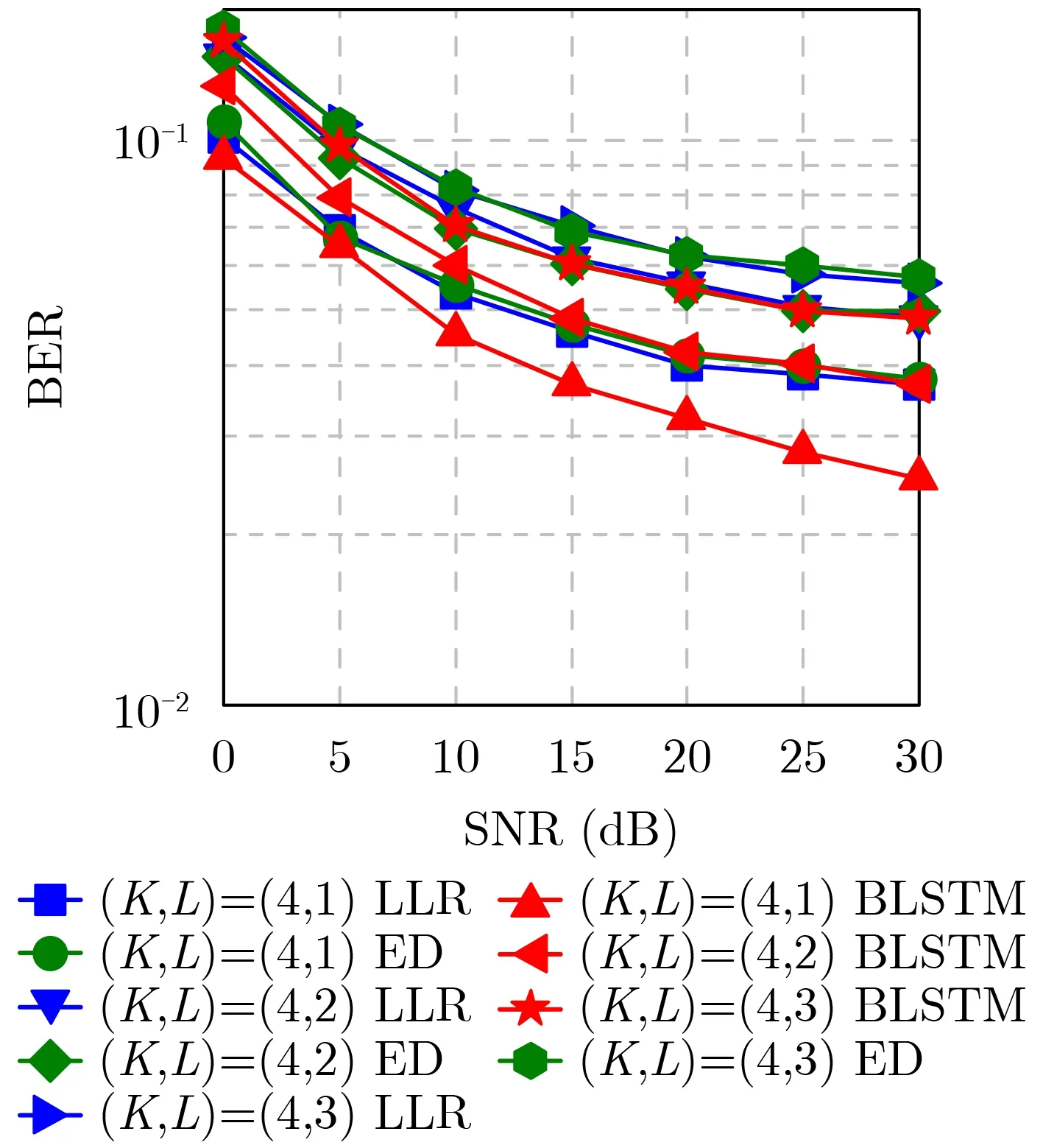
图5 不同模式下的BLSTM索引检测性能
为了进一步验证所提索引检测方法在不同通信场景下的鲁棒性,FBMC-IM系统的各项通信参数设置和BLSTM的各项网络超参数保持不变,加入时频聚焦特性各异的扩展高斯函数(Extended Gaussian Function, EGF)原型滤波器组进行仿真。表4对比了在(K,L)=(4,1)时 ,轴比例因子α分别为1/2, 1, 2时EGF滤波器下的IER。仿真结果表明表3的PHYDYAS滤波器与表4的EGF(α=2)滤波器IER相近,这两种滤波器具有比较好的时域聚焦特性,能够有效抑制符号间干扰即抵抗多径效应的能力更强,与当前信道特征一致。而各向同性的EGF(α=1)滤波器下的BLSTM检测的性能有所弱化,但仍优于传统算法。频率聚焦特性更佳的EGF (α=1/2)滤波器下的检测结果比ED, LLR差,这是由于此时所得的训练样本中未作处理的多径干扰更多,使得神经网络的特征提取效率大大下降。因次,BLSTM检测方法对于所选原型脉冲设计与当前信道时频特征的匹配程度较为敏感,所得的IER结果与选用的滤波器的性能成反比。
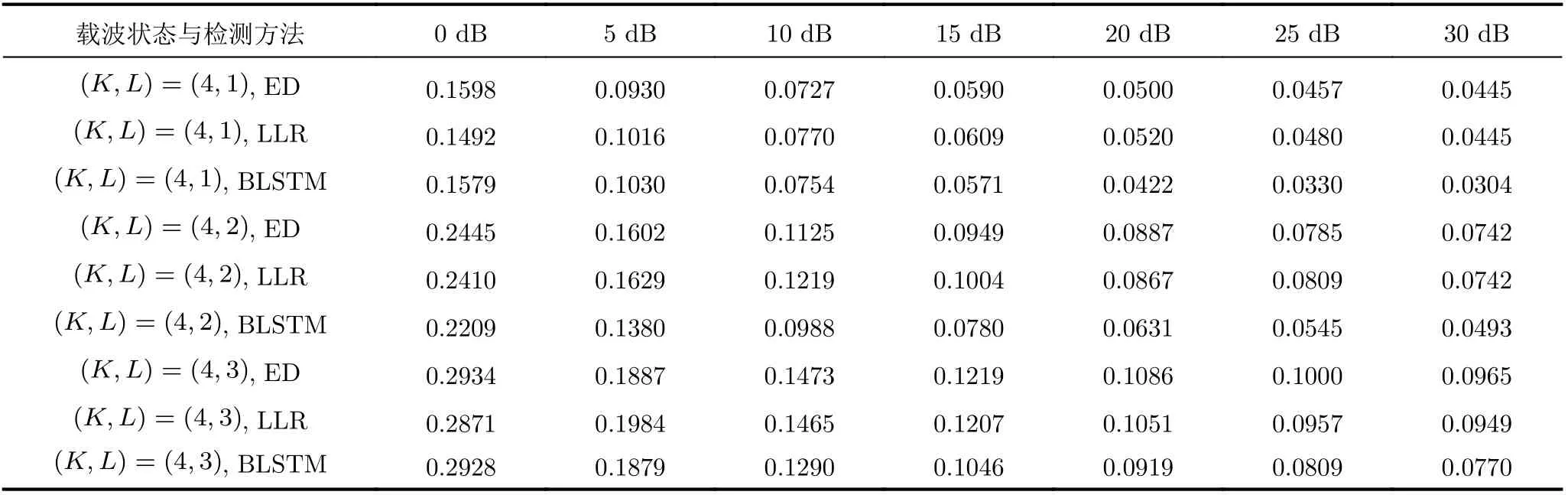
表3 各信噪比下活跃子载波位置检测误索引率(IER)

表4 ( K,L)=(4,1)时 不同α 值的EGF滤波器组系统误索引率(IER)
5 结论
在水声信号处理领域应用深度学习理论的思想逐渐得到了广泛的认可,本文提出一种结合BLSTM网络的子载波索引检测方法来降低水声多载波通信系统的误码率。不同于传统ED检测和LLR的逐载波比较,利用BLSTM网络对时间序列多元分类的思想进行整体子载波块索引识别,检测结果表明所得IER优于传统算法,有效降低了索引检测误码和星座符号检测误码。同时基于外场实验信道数据仿真分析了不同子载波占空比和不同原型滤波器选择下的系统性能,验证了所提方法的有效性和鲁棒性,有望成为索引调制机制下的通用检测手段。

