THE TIME DECAY RATES OF THE CLASSICAL SOLUTION TO THE POISSON-NERNST-PLANCK-FOURIER EQUATIONS IN R3*
Leilei TONG (童雷雷)
School of Science,Chongqing University of Posts and Telecommunications,Chongqing 400065,China
E-mail:tongleileitll@163.com
Zhong TAN (谭忠)
School of Mathematical Sciences and Fujian Provincial Key Laboratory on Mathematical Modeling&High Performance Scientific Computing,Xiamen University,Xiamen 361005,China
E-mail:ztan85@163.com
Xu ZHANG (张旭)†
School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450001,China
E-mail:xuzhang889@zzu.edu.cn
Abstract In this work,the Poisson-Nernst-Planck-Fourier system in three dimensions is considered.For when the initial data regards a small perturbation around the constant equilibrium state in a H3∩˙H-s(0≤s≤1/2) norm,we obtain the time convergence rate of the global solution by a regularity interpolation trick and an energy method.
Key words Poisson-Nernst-Planck-Fourier system;decay rates;energy method
1 Introduction
The Poisson-Nernst-Planck (PNP) system is a very important mathematical model describing the movement of charges under a concentration gradient and a electrostatic potential generated by themselves.The system has many applications such as in semiconductor technology,chemical science and biology (see[4,8,9,18,19,29,31,34,38–40]and the references therein).In the usual PNP model,the temperature is assumed to be homogeneous and independent of time.However,the heating effect plays a very important role in many applications.For example,in biological science (see[5,35]),the charge transport is found to be sensitive to changes in temperature.The ion-channels which are gated by the temperature will adjust the internal homeostasis and disease-related processes when the temperature changes.This suggests that it is necessary to take the influence of the temperature into consideration to fully understand the behavior of the electrothermal motion.In order to model the dynamic process with temperature,the mechanical equation should be coupled with the thermal equation.By an energetic variation method,the authors in[17,25]deduced the following Poisson-Nernst-Planck-Fourier (PNPF) equations:
Hereu0is the velocity of the solvent and satisfies
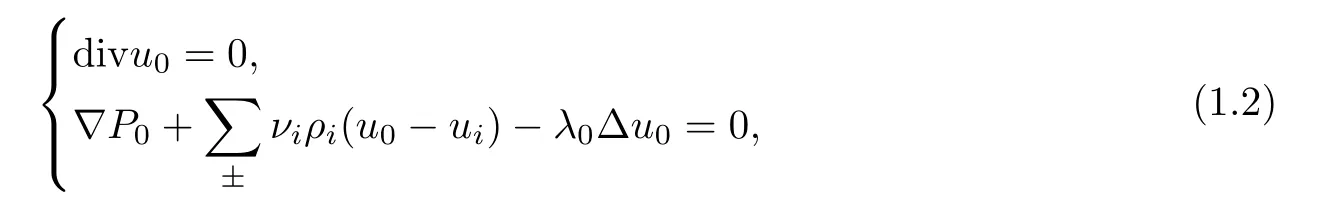
while,ρ+andz+are the density and the valence of cations,respectively.ρ-andz-are the density and valence of anions.ν+andν-are the diffusion coefficients.eis the elementary charge.kBis the Boltzmann constant.Tis the temperature.∈is related to the dielectric constant and the Debye length.u±denotes the flow map of cations and anions.C±andC0are the heat capacities of cations and anions of the solvent.kis the thermal conductivity.u0is the velocity of the solvent.λ0is the solvent viscosity.This system is inferred by employing the given free energy function and entropy production where the conservative forces are deduced by least action principle and the dissipative forces are inferred by the maximum dissipation principle.More details on the process of deducing this system can be found in[25].
WhileT=1 andu0is equal to some constant,the PNPF system will be reduced to the original PNP equations.One can check[23]and its references for a detailed derivation process of the PNP system.There have been a variety of studies on the well-posedness and the properties of the classical PNP equations and some modified versions.Gagneux and Millet[13]studied the well-posedness of the Nernst-Planck-Poisson system in both one dimension and higher dimensions,and obtained the global existence of the solution by using the Schauder-Tikhonov fixed-point method;they also established the properties (energy and entropy laws,influence of an external electrical field,Boltzmann distribution) of the global solution.By employing Schauder’s fixed-point theorem,Hsieh[15]obtained the global existence of the weak solution for a modified Poisson-Nernst-Planck system with steric effects in a bounded domain of Rd(d≤3).Ogawa and Shimizu[32]studied the well-posedness for a normalized Poisson-Nernst-Planck system in a 2Dcritical Hardy space H1(R2),then Deng and Li[6]considered the well-posedness and ill-posedness of this system in a 2DBesov space.One can check[3,12,27]for the well-posedness theories for some other modified systems.There are lots of works on the stability and the small parameter (as∈tends to zero) problems where the boundary layer may be involved;see[2,11,16,22]and the references therein.The steady problems were investigated in[1,10,24,33]and the singularly perturbed problems are discussed in[20,26].The authors in[17]consider the global existence of classic solutions to the PNPF system without a solvent equation.
The well-posedness theory and the problem of the time decay rate are important topics in the theory of partial differential equations.The continuity and continuous dependence on initial data of the unique solution are particularly important for problems arising from physical applications.In addition to this,the asymptotic behavior of the solution also attracts a lot of attention.In these cases,the primary mathematical tasks are to characterize the solution of the partial differential equations and show the explicit rate of convergence.While the initial data is near the constant equilibrium state in three dimensions,based on the energy method and the interpolation estimates,we want to investigate the global existence and the algebraic decay rate of the solution.As mentioned before,the purpose of the PNPF system is that it models the influence of the temperature on the movement of the charges.In particular,the system includes the solvent equation,which is much more physically accurate.From the point view of mathematics,the PNPF system couples the drift-diffusion equations with the nonlinear elliptic equation (1.2);the PNPF system (1.1) cannot be simply seen as the PNP equation and a temperature equation.This elliptic equation (1.2) brings difficulty to the proof.Indeed,by the properties of the elliptic operator,we cannot directly get theL2estimates ofu0.During the process of obtaining the a priori estimates,we need to avoid the presence of theL2norm ofu0.We will explain these things clearly after stating our main result.
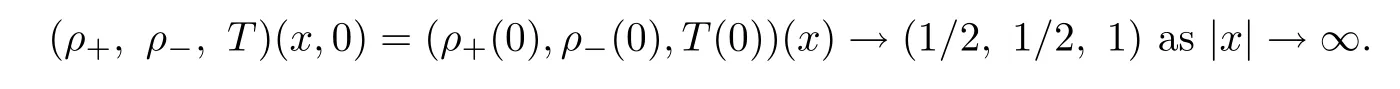
According to[25],the PNPF system is deduced by energy varaiation methods.The free energy and entropy dissipation can form a closed inequality.When we try to do the estimates inL2space,theirL2estimates cannot be closed,but this system can be closed in theH3norm.The densityρ0of the solvent is equal to some positive constant.We propose the initial condition Before stating the main result,we introduce some notations.‖f‖L2denotes theL2norm of the functionf.In a similar way,we can define the usual Sobolev norm ‖f‖H3.The notation ‖(f,g)‖H3means that ‖f‖H3+‖g‖H3.The normwiths≤0 is defined by,where F-1is the inverse Fourier transform.We denoteif there exists some constant~C,independent ofaandb,but dependent on the coefficients in (1.1),such thata≤b.In addition,in this work,the viscous coefficientsν±are equal and the valencesz+andz-are opposite.The main result of this work is as follows:
Theorem 1.1For some constant>0 small enough,which is only dependent on the coefficients in equations (1.1),if we have the initial data (ρ+(0),ρ-(0),T(0))∈HNwithN≥3,∇φ(0)∈L2and
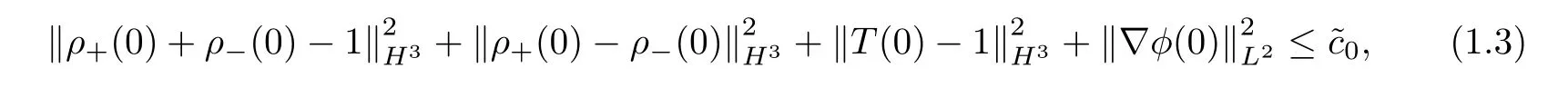
then system (1.1) admits a unique global classical solution which satisfies the following estimates for anyt>0:

Moreover,if we have the initial data (ρ+(0),ρ-(0),T(0))∈-swith 0≤s≤1/2,the solution has the following time decay rates fort≥0:
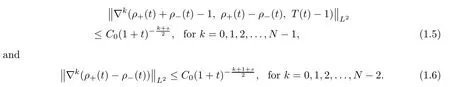
In the process of getting a priori estimates of the classical solution,the first step is to deduce the linear equations (A.2).Except for the Poisson equation,the solvent equation (1.2) is a nonlinear elliptic equation.This brings new difficulty in terms of the linearization and deducing the energy estimates.Noticing that the solvent equation is a type of steady Stokes equation,with the help of the Leray projector (see[37]),we can representu0by the density function and the electric field.As in[14,41,42],while the initial data is small enough,one can establish a priori estimates like

where Ek(t) and Dkare defined in (5.2).Based on (1.7),we can prove that
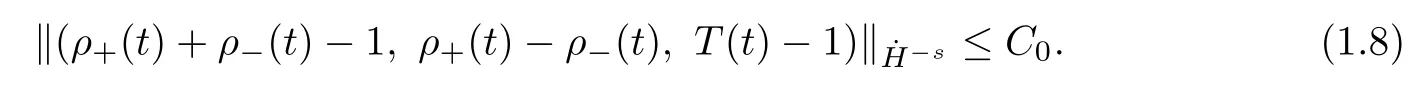
Then,with the help of the interpolation between positive and negative Sobolev norms (see Lemma A.4),one can infer that
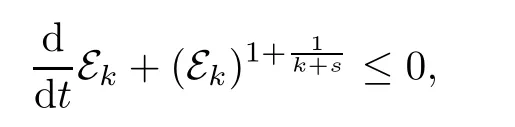
and obtain the time decay rates of the solution.
The nonlinear terms containingu0in the right hand side of (2.1) cannot be absorbed by the dissipation Dk,since the dissipation Dkdoes not containu0.To obtain (1.7) and (1.8),we must make full use of the structure of equations (2.1).With the help of (1.2) and (1.1)2and the Helmholtz projection,we can bound theL2estimates of∇u0by the electic field,which is the key point for closing the energy estimates.In the whole space,however,by the properties of elliptic operator,we cannot get theL2estimates ofu0.This is whysis less than one half.
Remark 1.2This theorem shows that the constant equilibrium state (1/2,1/2,1) is stable inH3space.Our result can be generalized to theNions case and to general constant equilibrium (see[21]for the existence of the general case).
Remark 1.3This work mainly studies the well-posedness and the time decay rates of the global solution around the constant equilibrium in R3.When the equilibrium state is no longer constant and with a strictly positive lower bound,one can obtain similar results,but the computation is very complicated and long.We will study this problem in a forthcoming paper.
The next sections are devoted to proving Theorem (1.1).The uniform estimates are deduced by the energy method in Section 2.We will construct the local classical solution and then extend the local solution to a global one in Section 3.The negative Sobolev estimates will be derived in Section 4.In addition,by a regularity interpolation trick,we get the time decay rates of the classical solution in Section 5.
2 The Energy Estimates of the Nonlinear Equations in L2 Norm
In this section,we will try to deduce the linearized equations and then infer the uniform estimates of the solution to the nonlinear equations (1.1).Motivated by[16],we can set

The linearized equations will become

A detailed calculation is included in Appendix A.For convenience,we introduce some notations,i.e.,defining
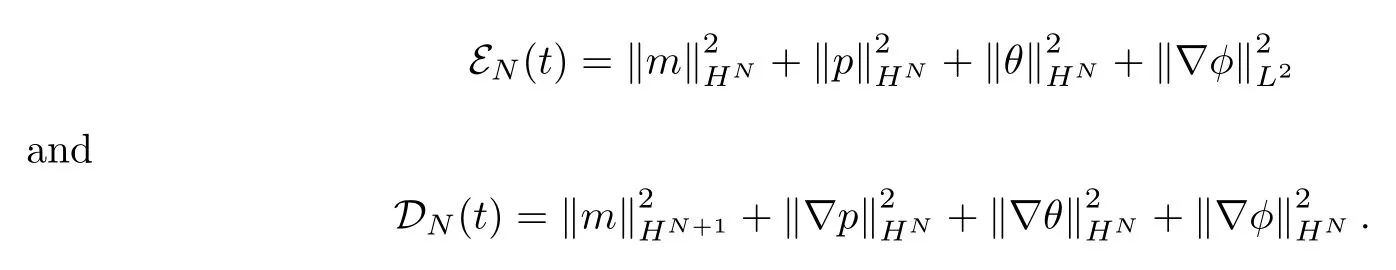
In order to derive the uniform estimates for the nonlinear system (2.1),we should assume the following a priori estimates for some sufficiently small~c0:
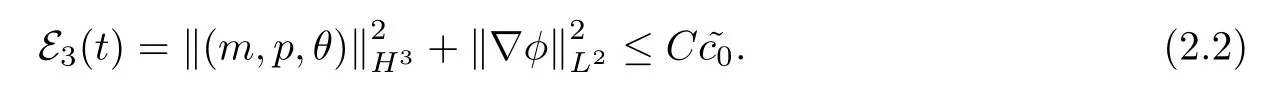
Since E3(t) is sufficiently small,it is enough to make sure that 1+pand 1+θhave the positive lower and upper bounds.
The main task in this section is to establish the following lemma:
Lemma 2.1Whilefor someT>0,there exists some constantcd>0 independent ofTsuch that

ProofWe apply the operator∇lwithl≥0 to equations (2.1) and multiply Equations (2.1)1,(2.1)2and (2.1)4by∇lm,∇lpand∇lθ,respectively,then integrate over R3,to obtain

Noticing that

Letcdbe the most minor amongIt follows that

Before estimating the nonlinear terms on the right hand side of (2.4),we get the estimates ofu0.By virtue of (1.2) and (1.1)2,we have that
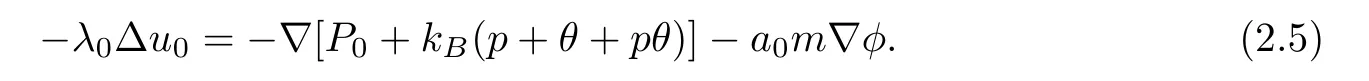
We can conclude that

In fact,we can multiply (2.5) byu0and employ integration by parts and Young’s inequality to get
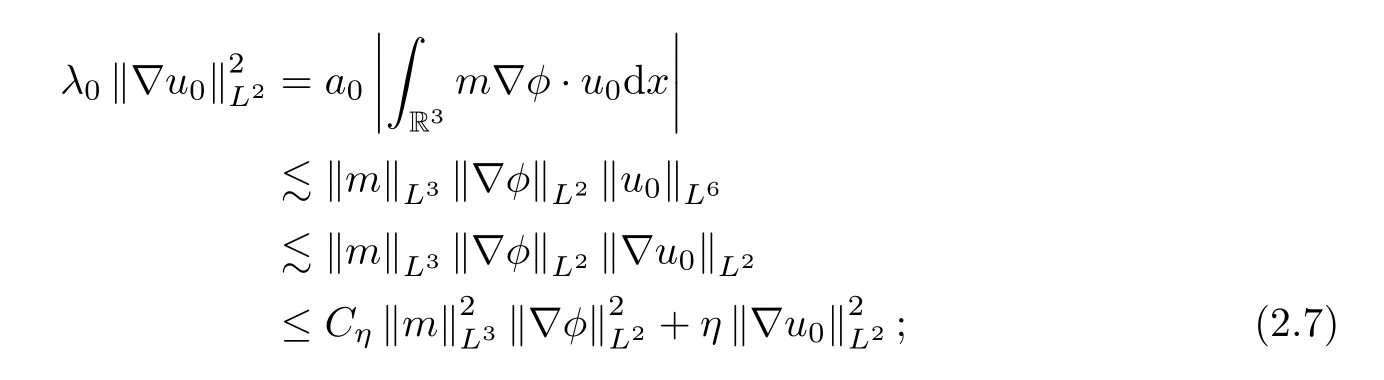
By[37],let Phbe the Helmholtz projection fromL2(R) to(R),where(R) is a subspace ofL2(R) with a divergence free vector in the distribution sense.Noticing thatu0is a divergence free vector,we then get

In virtue of (2.8),and with the help of the electric field equation,we can get that

Now,we turn to estimate the nonlinear terms on the right hand side of (2.4).By employing Hlder’s inequality,the product estimates (A.4) of Lemma A.2,and Gagliardo-Nirenberg’s inequality (A.3),we can deduce that

We derive,by using integration by parts,Hlder’s inequality and the product estimates (A.4) of Lemma A.2,that

With the help of (2.6) and (2.9),we can deduce that
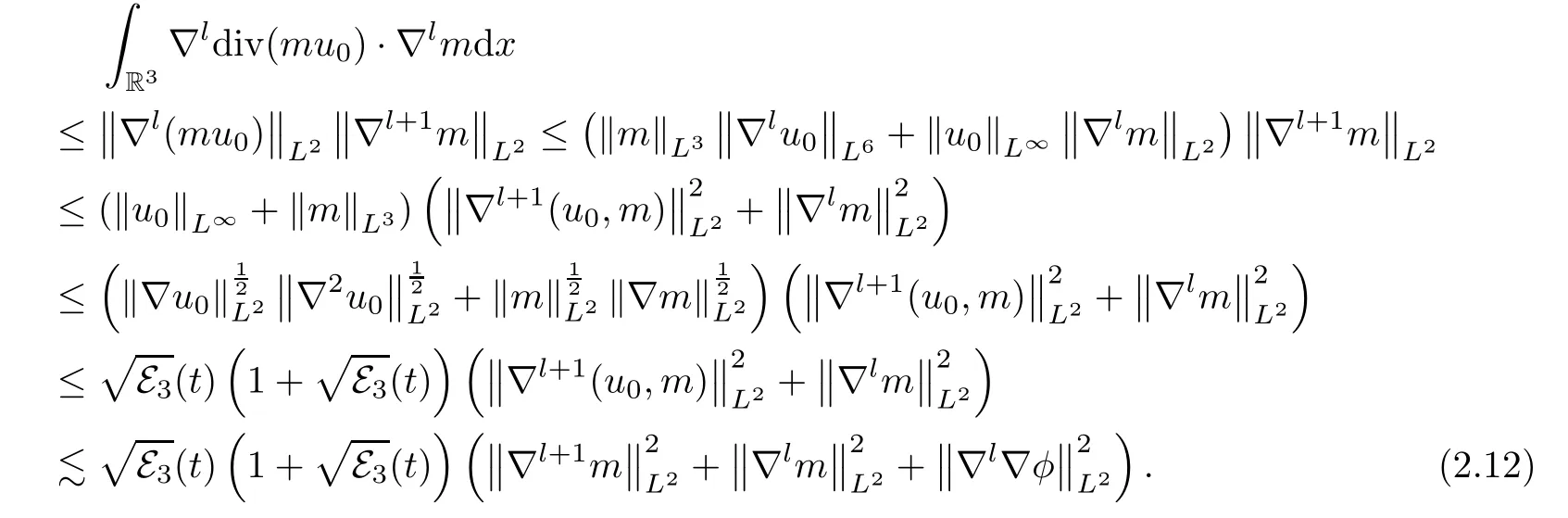
It follows from (2.10)-(2.12) that
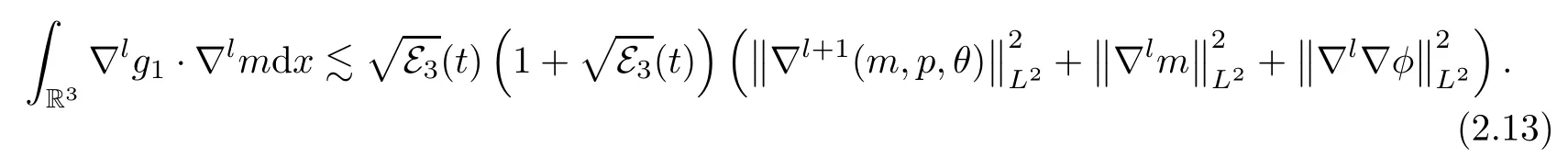
Since the dissipation DN(t) does not contain∇lp,the term div (pu0) ing2cannot be estimated the same in (2.12).We must deal with this term carefully.Whenl=0,by the fact that divu0=0 and (2.6),we can infer that
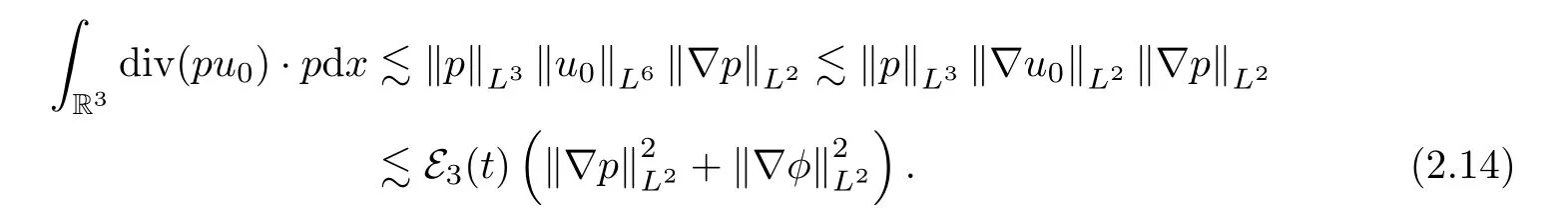
Whenl≥1,by integration by parts,Hlder’s inequality,the product estimates (A.4) of Lemma A.2 and Gagliardo-Nirenberg’s inequality (A.3),we get

By virtue of (2.6) and (2.9) withl=1,we can deduce that

Plugging (2.16) into (2.15),together with (2.14),we get forl≥0 that
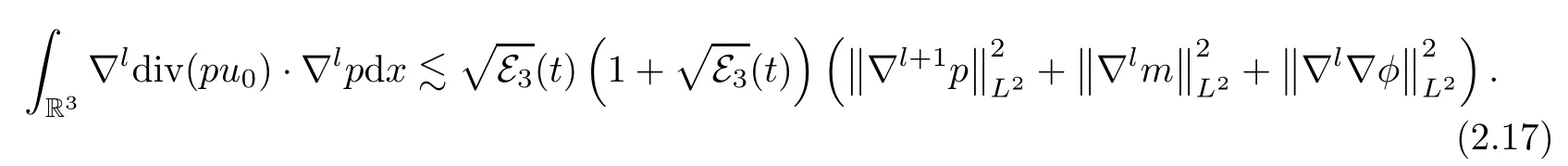
The other two terms ing2can be estimated by an argument similar to that of (2.10) and (2.11).Thus,we have
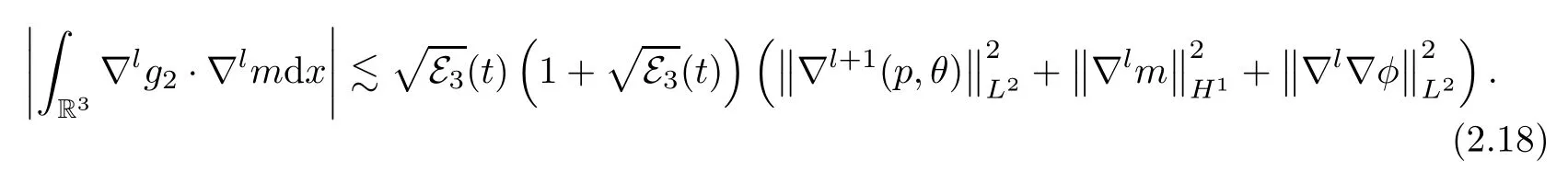
Forgi,i≥3,since the denominator containsd0+d+p+d-m,the strict positive lowerL∞bound ofd0+d+p+d-mis needed.Under the assumption of the a priori estimates (2.2),there existssuch that

In what follows,we deal withgi(i≥3).Whenl=0,it holds that
Whenl≥1,we can use integration by parts,Hlder’s inequality,the product estimates (A.4) of Lemma A.2 and Gagliardo-Nirenberg’s inequality (A.3) to give that

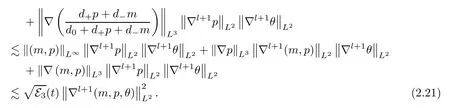
The second term ing3can be estimated by the same argument as that in (2.21).Thus,forl≥0,we finally have

For the termg4,whenl=0,by the facts (2.19) and (2.6),we have that

For whenl≥1,we will estimate each term ofg4.By Hlder’s inequality,we get that


By the product estimates (A.4) of Lemma A.2 and Gagliardo-Nirenberg’s inequality (A.3),we have that
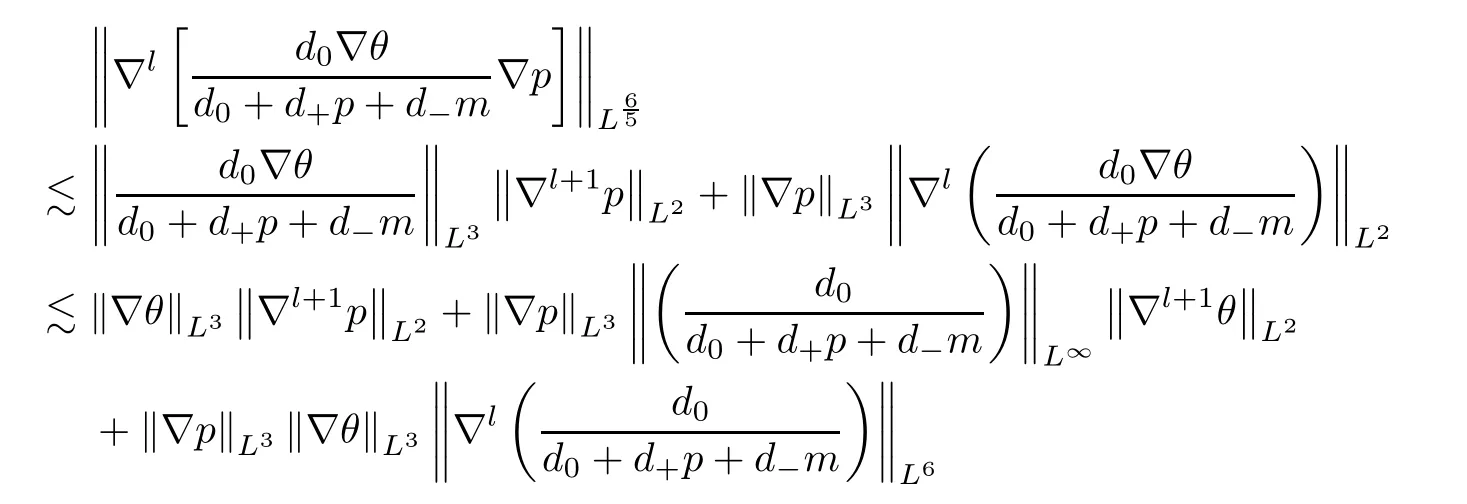

We can estimate the rest of the terms ofg4by arguments similar to those in (2.26)–(2.27) and (2.15)–(2.17).Thus,we have

In what follows,we will estimate the termg5.The termg5will be divided into four terms.First of all,we want to get the estimates of the first term ofg5.By employing integration by parts and Hlder’s inequality,it follows that
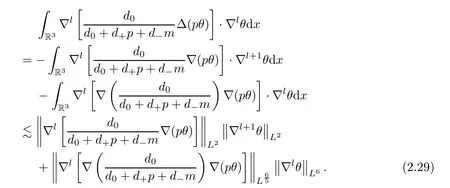
From (2.29),forl=0,it is clear that

Forl≥1,by employing the product estimates (A.4) of Lemma A.2 and Gagliardo-Nirenberg’s inequality (A.3),we can deduce that

The estimates (2.31)–(2.32),together with (2.30),finally give that
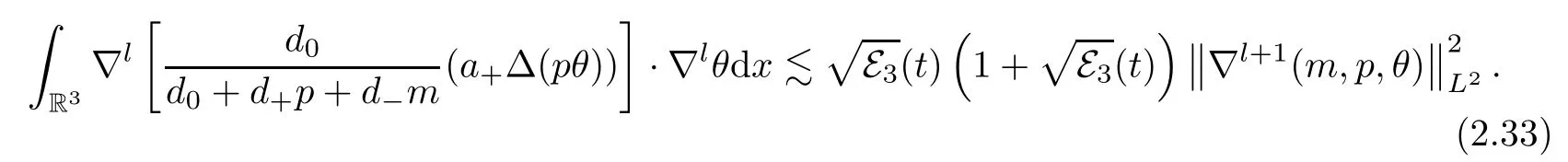
Second,for the second term ofg5,with the help of (2.19),it is clear that forl=0,
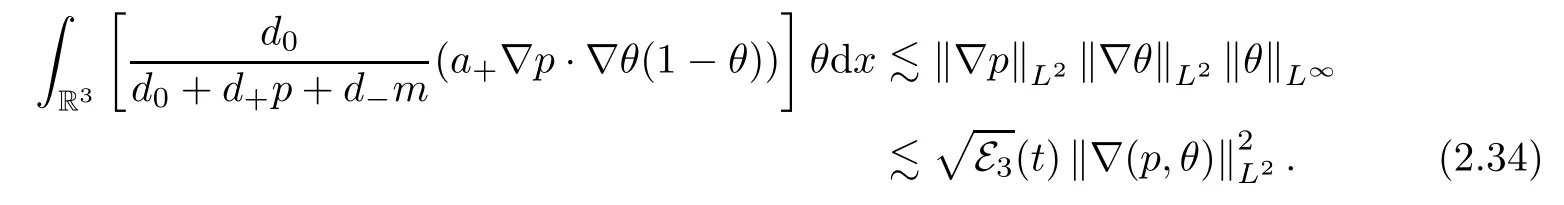
Whilel≥1,we can use Hlder’s inequality,the product estimates (A.4) of Lemma A.2 and Gagliardo-Nirenberg’s inequality (A.3) to obtain that
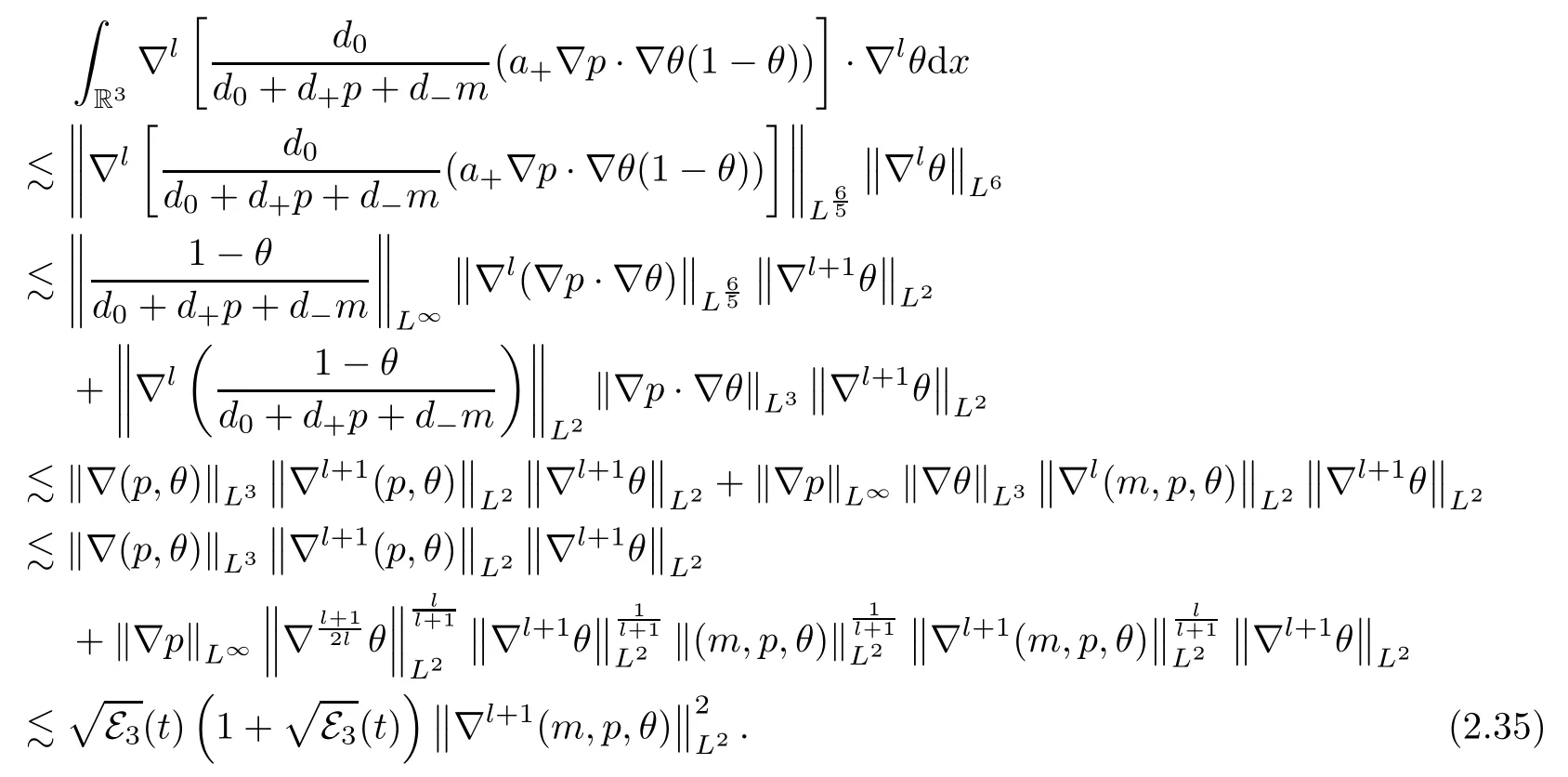
From (2.34) and (2.35),it holds forl≥0 that
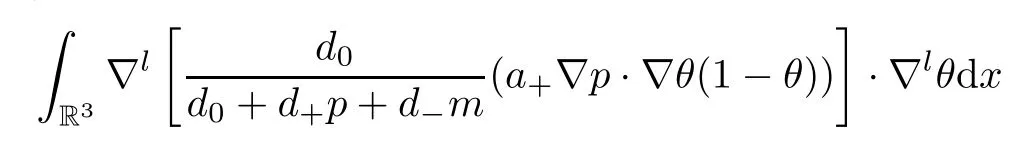

Next,we estimate the third term ofg5.It holds,by employing integration by parts,that
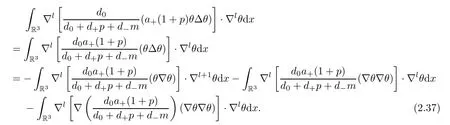
For whenl=0,it is clear that

Forl≥1,by using Hlder’s inequality,the product estimates (A.4) of Lemma A.2 and Gagliardo-Nirenberg’s inequality (A.3),we get that
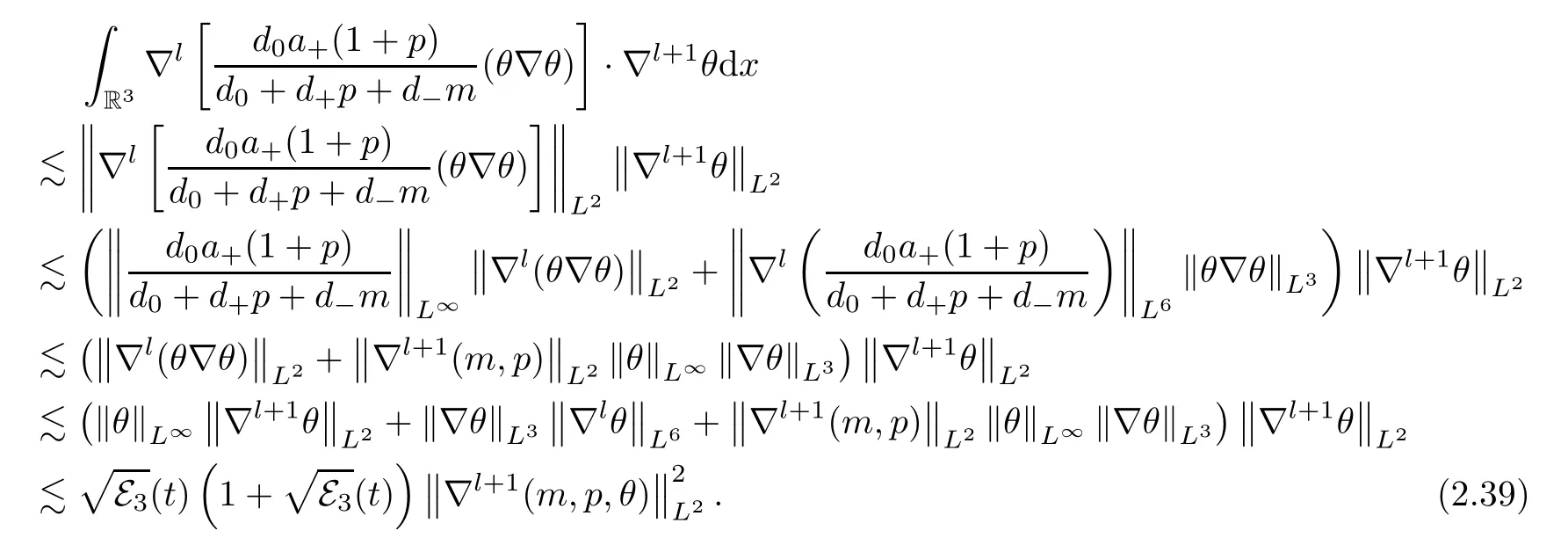
The other two terms in (2.37) can be dealt with by the routine of using Hlder’s inequality and Gagliardo-Nirenberg’s inequality (A.3).We can employ an argument similar to that of (2.39) to deduce that
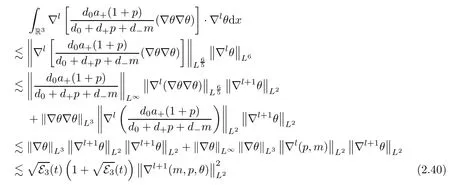
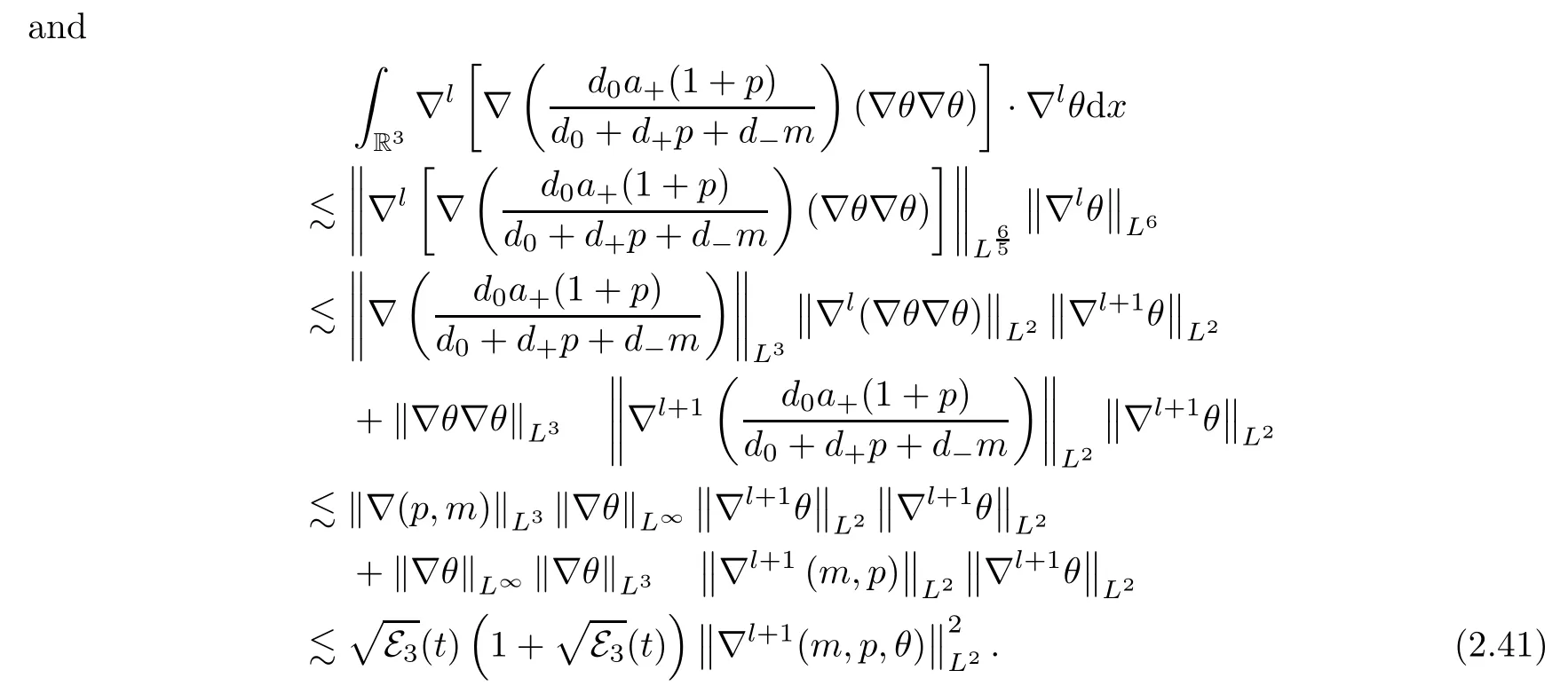
Plugging (2.39)-(2.41) into (2.37),together with (2.38),it holds forl≥0 that
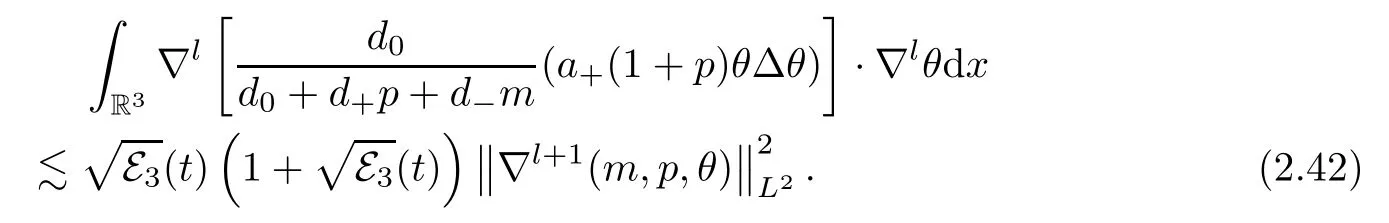
Finally,we deal with the last term ofg5.Forl=0,we have that

Whenl≥1,by employing Hlder’s inequality,the product estimates (A.4) of Lemma A.2 and Gagliardo-Nirenberg’s inequality (A.3),we have that

Thus,forl≥0,we finally get that

In terms of (2.33),(2.36),(2.42) and (2.43),we get that

By an argument similar to that for estimates (2.40),we can get that
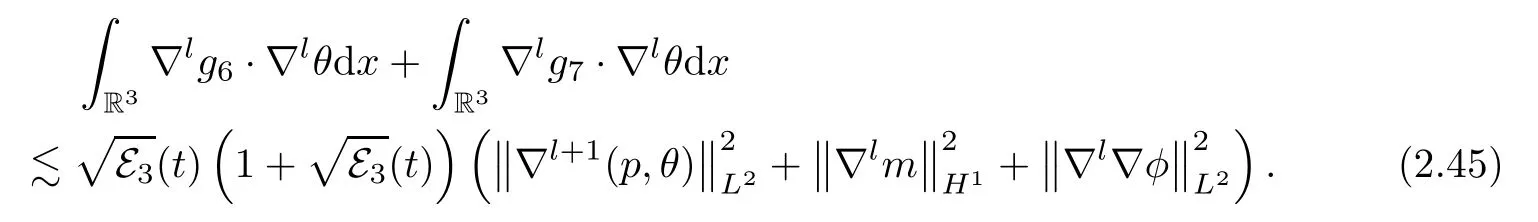
In light of (2.13),(2.18),(2.22),(2.28),(2.44) and (2.45),we obtain that
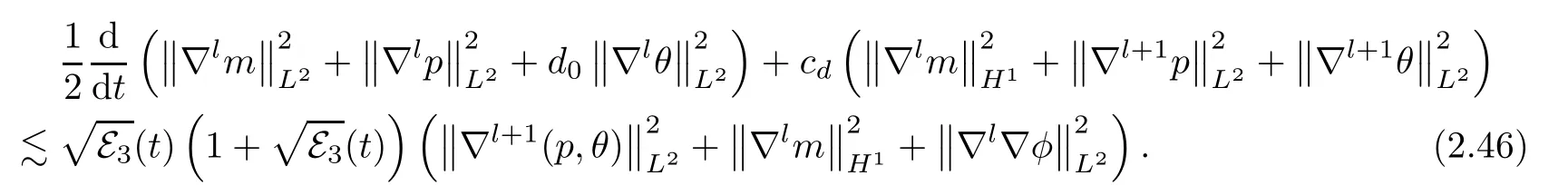
Unfortunately,we note that the term∇l∇φappearing on the right hand side of (2.46) can not be absorbed by the left hand side;that is,the energy estimates cannot be closed.Therefore,we must obtain the estimates of∇φ,since this is necessary to close the energy estimates.Plugging (2.1)3into equation (2.1)1,we get that

We can apply the operator∇lwithl≥0 to equations (2.47) and multiply by∇lφto deduce that
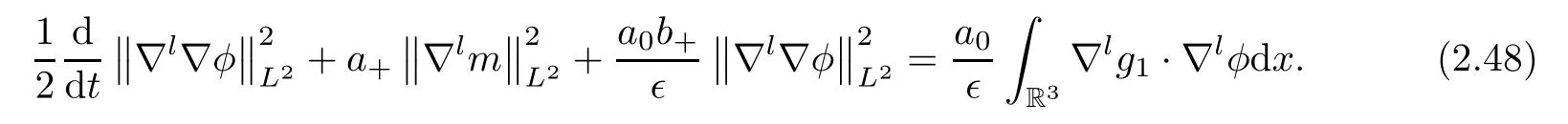
Integration by parts,together with Hlder’s inequality,implies that

A similar argument to that of (2.49) gives rise to
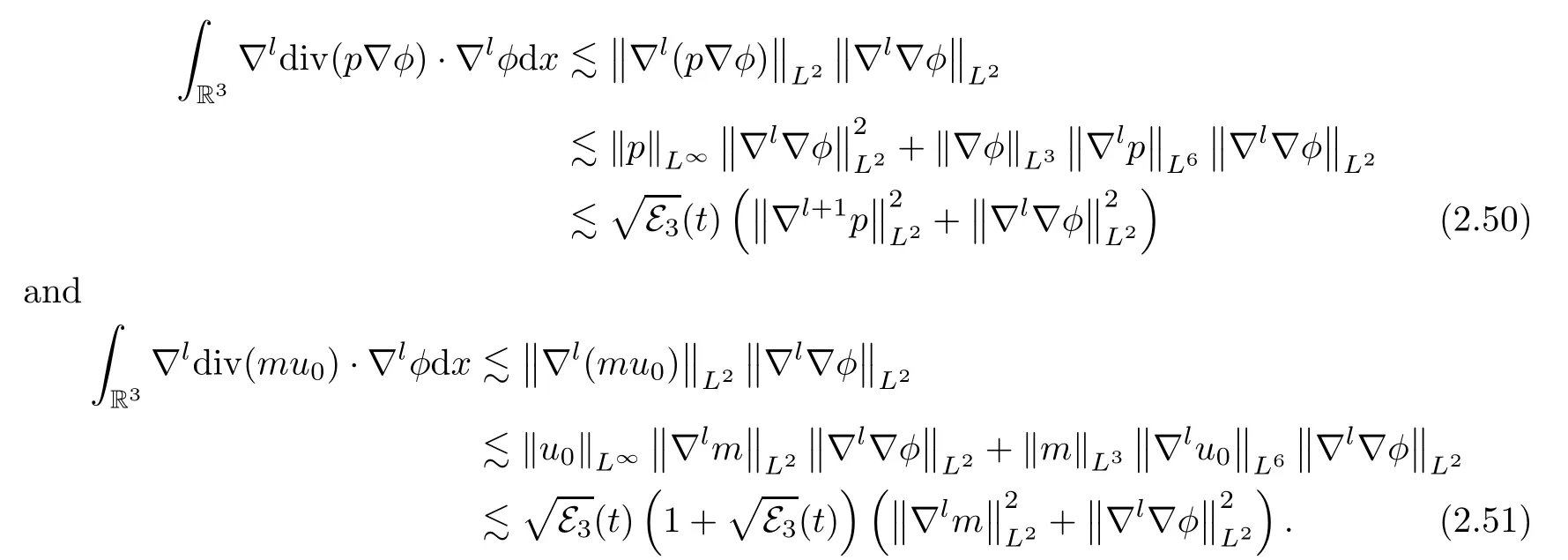
It follows from (2.48)–(2.51) that
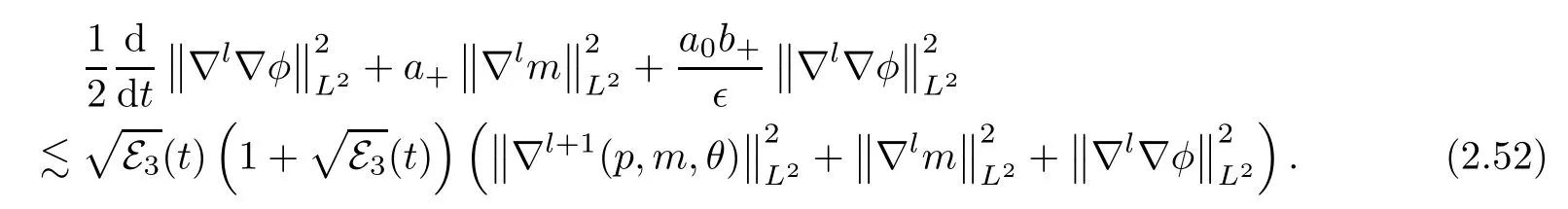
Summing up (2.52) and (2.46),we can obtain (2.3). □
From Lemma 2.1,we directly obtain the uniform estimates as follows:
Proposition 2.2If there is some sufficiently small~c>0 and someT>0 such that

then it holds forN≥3 that
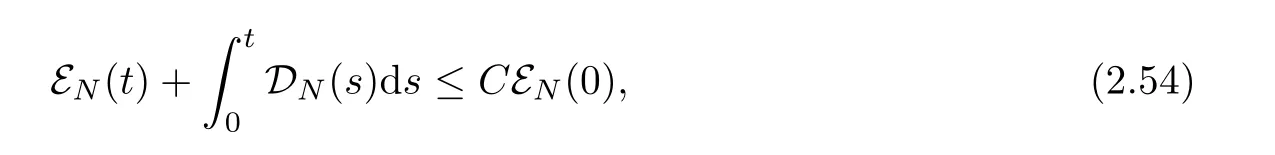
which proves (1.4) of Theorem 1.1.By a standard continuity argument,the a priori estimates (2.2) can be closed when we takeN=3.
3 Approximate Solutions and Global in Time Solution
3.1 Local in time solution
In this section,we will try to construct the local in time solution to (1.1) under the assumptions of Theorem 1.1.We shall sketch the idea of constructing the approximate solutions by an iteration method.These processes are routine.The approximate system is as follows:
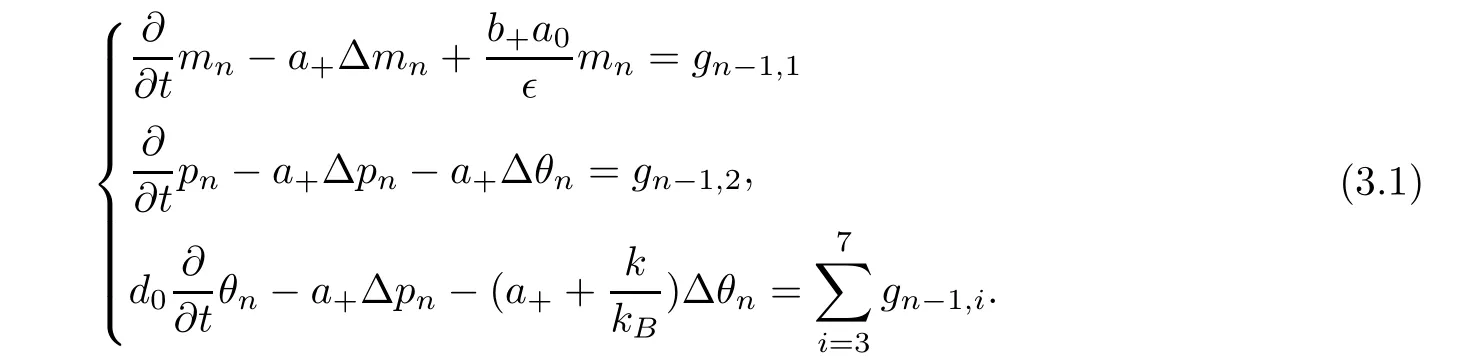
Heregn-1,i(1≤i≤7) are likegi,in which the unknownsp,m,θ,φ,u0are replaced bypn-1,mn-1,θn-1,φn-1,u0,n-1.In particular,
Letp0=0,m0=0,θ0=0,u0,0=0,and

For eachn∈N+,system (3.1) is reduced to the linear parabolic one with source terms.By the parabolic theorem,the existence of aH3solution to system (3.1) can be established while the source terms belong to theH2space.In what follows,we will show how to deduce theH2bound of the source terms for eachn∈N+.

Whenn=1,the source terms vanish.In a manner similar to that used to deduce (2.4),we obtain that
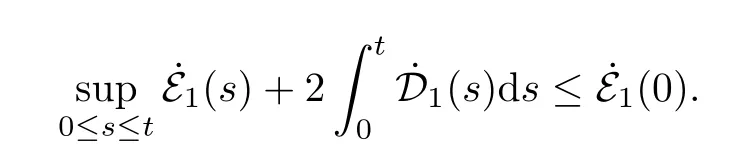
By arguments similar to (2.13),(2.18),(2.22),(2.28),(2.44) and (2.45),and according to (2.54),we can deduce that
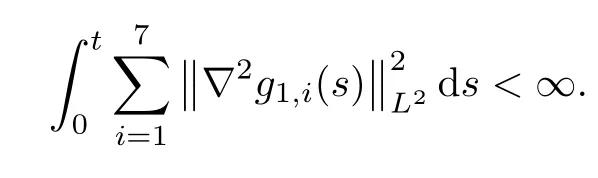
By induction,we can infer that,for anyn∈N+andt>0,
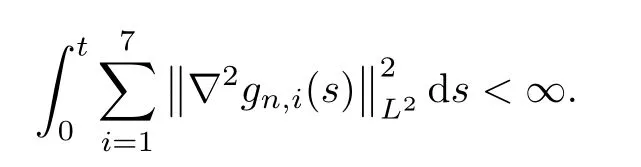
Recalling that there exists the denominatord0+d+p+d-min eachgn,i(3≤i≤7,we have that the denominator must be positive with a strict lower bound.This also requires that the initial data should be small in theH3sense.With the help of (2.13),(2.18),(2.22),(2.28),(2.44),(2.45) and (2.54),by employing the Picard iteration method and the induction method,we can deduce the uniform upper bound of theH3bound of approximate solutions with respect ton∈N+for small enoughT>0;by the Sobolev embedding inequality,theirH3norm can be obtained.Then for small enough time,we can prove that (pn,mn,θn) is a Cauchy sequence in theH3norm and the uniqueness of the local in time solution can be obtained.
3.2 Global solution
By combining the local in time existence and the uniform estimates (2.54),we can get the global classical solution in the framework of[28].
4 The Estimates in˙H-s Norms
In this section,we are trying to deduce some useful estimates of the solution in the negative Sobolev norms.These estimates will be very helpful in the process of deducing the time decay estimates of the solution.
Lemma 4.1It holds fors∈[0,1/2]that
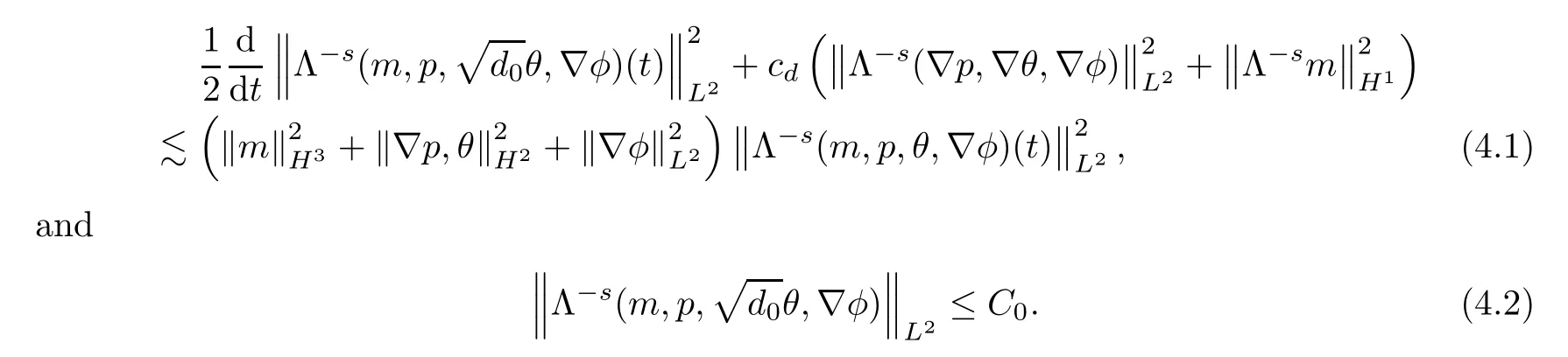
ProofWe apply the operator Λ-sto equations (2.1)1,(2.1)2and (2.1)4,and multiply by Λ-sm,Λ-spand Λ-sθ,respectively,then integrate over R3,to deduce that

It follows that

Now,we estimate the nonlinear terms on the right-hand side of (4.3).Employing estimates (A.5) in Lemma A.3 and Gagliardo-Nirenberg’s inequality (A.3),we can get that

An argument similar to that of (4.4) gives that
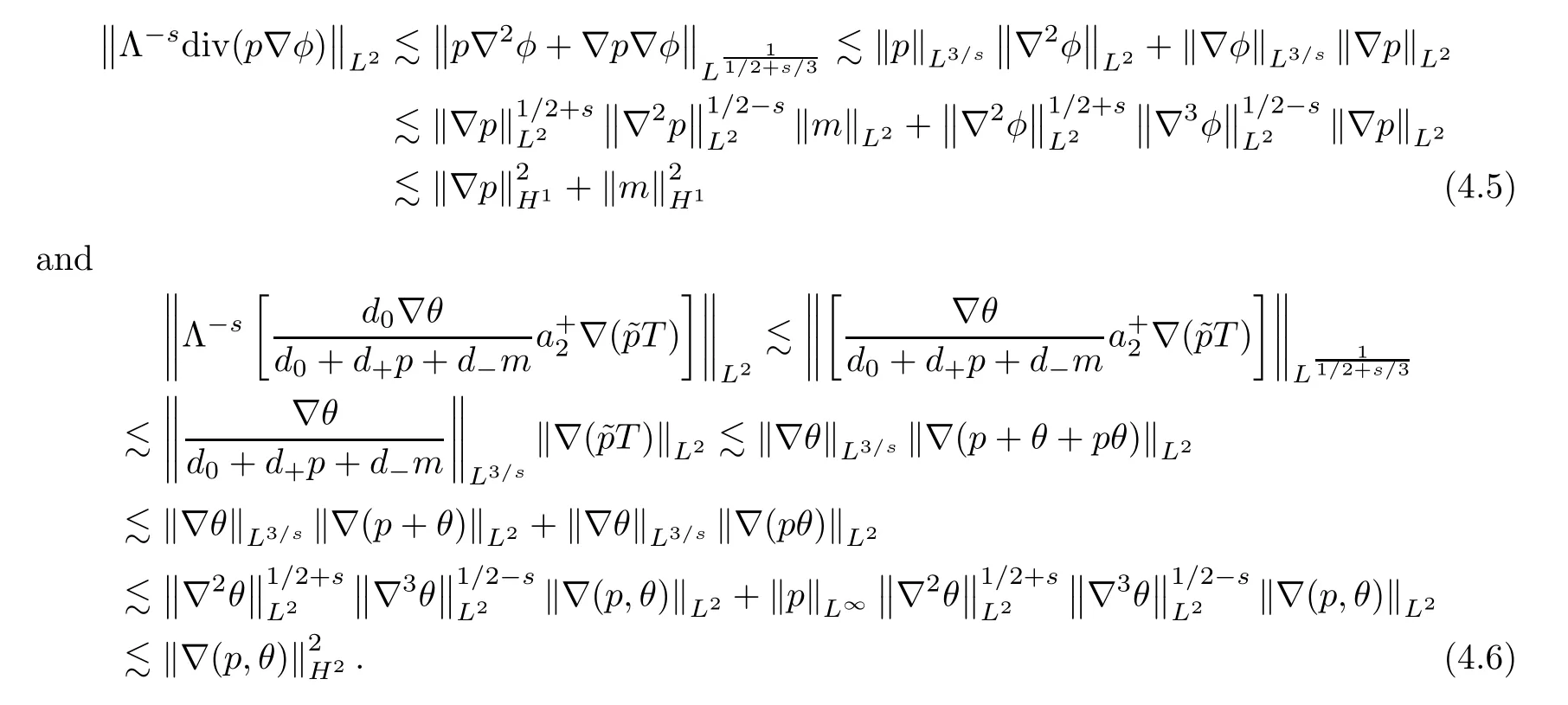
Because divu0=0,we can obtain that

The rest of the terms ingican be estimated in a manner similar to (4.4)–(4.7).Then,we get that
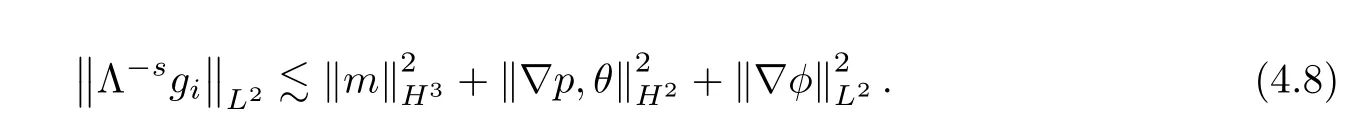
By (4.8) and (4.3),we can deduce (4.1).
We denote E-s(t) to be equivalent to.From (2.54),we can takeN=3 to get that

With this fact,we can integrate (4.1) in time to obtain that
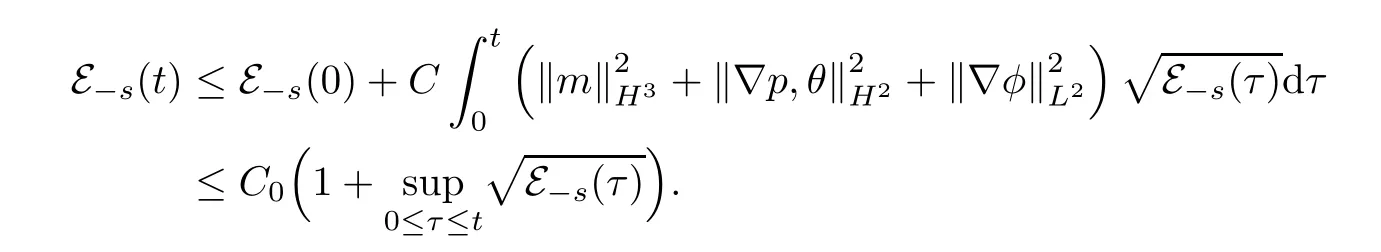
This implies (4.2) fors∈[0,1/2]. □
5 Time Decay Rates of the Global Solution
In this section,we will prove the decay rates.First,we use (A.6) of Lemma A.4 and (4.2) to obtain,fors∈[0,1/2]andk+s>0,that

We take
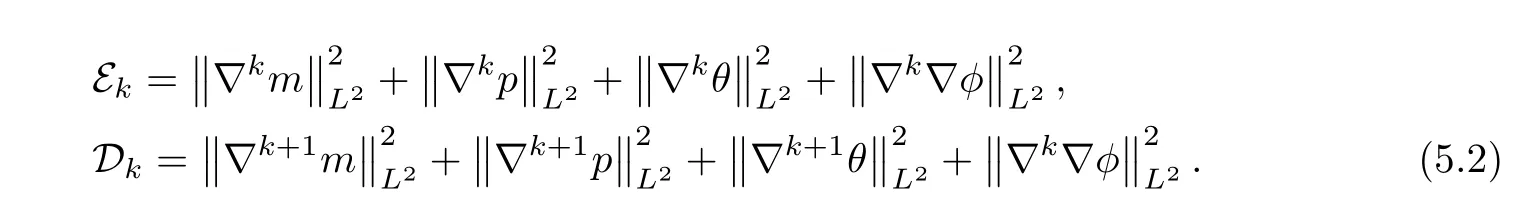
By (5.1),we obtain that

By (2.3) and (5.3),we deduce that

By solving the inequality above,we obtain that

Then we prove (1.5).With the help of the electric field equation,we can easily get (1.6) from (1.5).The proof of Theorem 1.1 is completed.
Appendix
In this appendix,we give the main steps for deducing the linearized equations (2.1).

and then,by (A.1) and (1.1)2,we have that
It is likely that we can get that
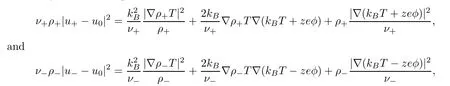
which imply that

From the solvent equation (1.2),we have thatBy virtue of the Leray project operator,no linear term can be split fromu0.Whenb-=0,we can get the closedL2estimates for any∈.
In what follows,we list some useful inequalities which are frequently used for obtaining the energy estimates of the solution.
Lemma A.1(Gagliardo-Nirenberg’sinequality) The parameters satisfy that 0≤k,m≤land 2≤p≤∞,so we have that
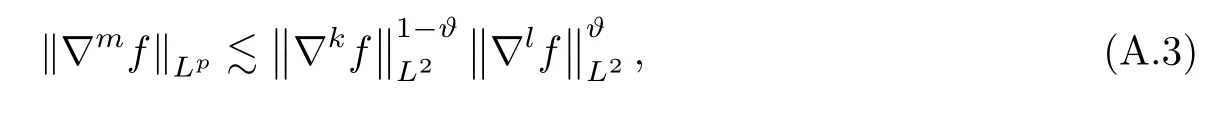
where 0≤ϑ≤1 andmsatisfies

Notice that ifp=∞,we require that 0<ϑ<1.
ProofThe detailed proof can be seen in[30],p.125. □
Lemma A.2(Product estimates) For the integerl≥0,we have that

The parametersp,p1,p2andp3∈[1,+∞]satisfy 1/p=1/p0+1/p1=1/p2+1/p3.
ProofWe can prove this lemma in the same way as Lemma A.1 in[7]. □
Lemma A.3(Sobolev embeding inequality) If 0≤s<3/2,it holds that

where 1<p≤2 and 1/2+s/3=1/p.
ProofSee[36]p.119,Theorem 1. □
Lemma A.4Suppose thats,ℓ≥0.Then we have

ProofOne can see Lemma A.4 in[14]for the detailed proof. □
 Acta Mathematica Scientia(English Series)2022年3期
Acta Mathematica Scientia(English Series)2022年3期
- Acta Mathematica Scientia(English Series)的其它文章
- A ROBUST COLOR EDGE DETECTION ALGORITHM BASED ON THE QUATERNION HARDY FILTER*
- CONTINUOUS SELECTIONS OF THE SET-VALUED METRIC GENERALIZED INVERSE IN 2-STRICTLY CONVEX BANACH SPACES*
- EXISTENCE RESULTS FOR SINGULAR FRACTIONAL p-KIRCHHOFF PROBLEMS*
- BOUNDS FOR MULTILINEAR OPERATORS UNDER AN INTEGRAL TYPE CONDITION ON MORREY SPACES*
- LEARNING RATES OF KERNEL-BASED ROBUST CLASSIFICATION*
- A COMPACTNESS THEOREM FOR STABLE FLAT SL (2,C) CONNECTIONS ON 3-FOLDS*
