The Three-Pion Decays of the a1(1260)∗

Xu Zhang(张旭)and Ju-Jun Xie(谢聚军)

Institute of Modern Physics,Chinese Academy of Sciences,Lanzhou 730000,China

University of Chinese Academy of Sciences,Beijing 101408,China

1 Introduction

In the naive quark model,mesons are composed of a quark-antiquark pair.This picture works extremely well for most of the known mesons.[1]However,there are a growing set of experimental observations of resonancelike structures,which cannot be explained by the quarkantiquark model.[1−3]Even among the seemingly well established and understood mesons,some of them may be more complicated than originally thought.[4−5]One such example is the lowest-lying axial-vector mesons.The a1(1260)is a ground state of axial-vector resonance with quantum numbers IG(JPC)=1−(1++).However,it was found that the a1(1260)could be dynamically generated from the interactions of K∗¯K and ρπ channels and the couplings of the a1(1260)to these channels can be also obtained at the same time.[6]Based on these results,the radiative decay of a1(1260)meson was studied in Refs.[7–8],where the theoretical calculations agree with the experimental values within uncertainties.In Ref.[9]the lattice result for the coupling constant of a1(1260)to the ρπ channel is also close to the value obtained in Ref.[6].Besides,the effects of the next-to-leading order chiral potential on the dynamically generated axial-vector mesons were studied in Ref.[10].It was found that the inclusion of the higher-order kernel does not change the results obtained with the leading-order kernel in any significant way,which gives more supports to the dynamical picture of the a1(1260)state.[6,10−11]

On the other hand,it is suggested that the a1(1260)resonance is a candidate of the chiral partner of the ρ meson[12−14]described as a q¯q state.The nature of a1(1260)has been studied by calculating physical observables such as the τ decay spectrum into three pions[15−18]or the multipions decays of light vector mesons.[19−20]Recently,the production of a1(1260)resonance in the reaction of π−p →(1260)p within an effective Lagrangian approach was studied in Ref.[21]based on the results obtained in chiral unitary approach.Furthermore,a general method was developed in Ref.[22]to analyze the mixing structure of hadrons consisting of two components of quark and hadronic composites,and the nature of the a1(1260)was explored with the method,[22]where it was found that the a1(1260)resonance has comparable amounts of the elementary component q¯q to the ρπ.In Ref.[23],the Ncbehavior of a1(1260)was studied using the unitarized chiral approach,and it was found that the main component of a1(1260)is not q¯q.A probabilistic interpretation of the compositeness at the pole of a resonance was been derived in Ref.[24],where it was obtained that,for a1(1260),the compositeness and elementariness are similar.Furthermore,the a1(1260)can also appear as a gauge boson of the hidden local symmetry,[25−26]which is recently reconciled with the five-dimensional gauge field of the holographic QCD.[27−28]Yet,the nature of the a1(1260)state is still not well understood.The only way to understand its nature is to examine it from all possible perspectives,both experimentally and theoretically.

On the experimental side,for the a1(1260)resonance,the experimental width Γa1(1260)=(250–600)MeV as-signed by the Particle Data Group(PDG)[1]has large uncertainty.While most experiments and phenomenological extractions agree on the mass of the a1(1260)leading to a PDG value of Ma1(1260)=(1230±40)MeV,which is more precisely than its width.A new COMPASS measurement in Ref.[29]provides a much smaller uncertainty of the width Γa1(1260)=367±MeV and mass Ma1(1260)=1255±6+7−17MeV.Therefore,study of the total decay width and the decay behaviors of a1(1260)is important both on experimental and theoretical sides,and can also provide beneficial information about the internal structure of it.

The best knowledge about a1(1260)resonance decay channels and branching ratio comes from hadronic τ decay measurements,[30−32]while the ρπ decay mode in the three-pion decays,which the dominant decay channel of a1(1260),is the most important one.[1,33−34]In this work,we study the three-pion decays of the a1(1260)by considering only the dominant a1(1260)→ ρπ intermediate process and,in this calculation,we take the coupling constant of a1(1260)to ρπ channel in S-wave as that was obtained in Ref.[6].In this respect,our calculations are based on the dynamical picture of the a1(1260),which is a dynamically generated state from the interactions ofK∗and ρπ coupled channels.We calculate the energy dependence of the partial decay width of Γa1(1260)→3πas a function of the mass of a1(1260),which could be tested by future experiments when the precise measurements for the mass and width of the a1(1260)resonance were done.

This article is organized as follows.In Sec.2,formalism and ingredients used in the calculation are given.In Sec.3,the results are presented and discussed.Finally,a short summary is given in the last section.

2 Formalism and Ingredients

We study the decay of a1(1260)→ 3π with the assumption that the a1(1260)is dynamically generated from the interactions of ρπ andK∗in coupled channel,thus this decay can proceed via a1(1260)→ ρπ → 3π as shown in Fig.1,where we take the(1260)→ π+π+π−and π+π0π0into account.It is easy to know that the two diagrams in Fig.1 give the same contributions to the a1(1260)→ 3π decay.Hence,we consider only the Fig.1(a)in the following calculation and we multiply by a factor two to the final result.

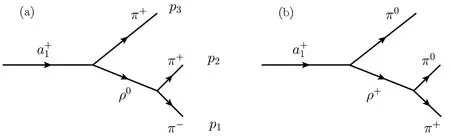
Fig.1 The dominant diagrams for the decay of a1(1260)→ 3π.(a)(1260)→ π+π+π− and(b)(1260)→ π+π0π0.

2.1 Decay Amplitude at Tree Level

In order to evaluate the partial decay width of a1(1260)→ 3π,we need the decay amplitudes of the tree level diagrams shown in Fig.1,where the process is described as the a1(1260)decaying to ρπ and then the ρ decaying into ππ.As mentioned above,a1(1260)results as dynamically generated from the interactions of the ρπ andK∗in coupled channels.We can write theρ0π+vertex as

whereis the polarization vector of a1(1260)and εµthe polarization vector of the ρ.The ga1ρπis the coupling of the a1(1260)to the ρπ channel and can be obtained from the residue in the pole of the scattering amplitude in I=1.We take ga1ρπ=(−3795+i2330)MeV and ga1K¯K∗=(1872−i1468)MeV as obtained in Ref.[6].We can see that the a1(1260)has large coupling to ρπ channel comparing to theK∗channel.

To compute the decay amplitude,we also need the structure of the ρππ vertices,which can be evaluated by means of hidden gauge symmetry Lagrangian describing the vector-pseudoscalar-pseudoscalar(VPP)interaction,[25,35−37]given by

where the symbolstands for the trace in SU(3)and g=mV/2f,with mV=mρand f=93 MeV the pion decay constant.The matrices P and V contain the nonet of the pseudoscalar mesons and the one of the vectors respectively.

From the Lagrangian of Eq.(2),the vertex of ρ0π+π−can be written as‡‡Note that from the local hidden gauge approach is 5.89,while the equivalent quantity gρππ used in Ref.[38]is 6.05.They differ in 2.5%.

where p1and p2are the momenta of π−and π+mesons,respectively.

We can now straightforwardly construct the decay amplitude for(1260)→ π+π+π−decay corresponding to the tree diagram shown in Fig.1(a):

where the two terms stand for the contributions with the ρ0in theand in thesubsystem,and q1=p1+p2and q2=p1+p3.

We take the energy dependent decay width of Γρ.Because the dominant decay channel of ρ is ππ,we take

with Γon=149.1 MeV,and

withthe invariant mass square of the π+π−system corresponding the two terms shown in Eq.(4).We take mρ=775.26 MeV in this work.

It is worthy to mention that the parametrization of the width of the ρ meson shown in Eq.(5)is common and it is meant to take into account the phase space of each decay mode as a function of the energy.[39−41]In the present work we take explicitly the phase space for the P-wave decay of the ρ into two pions.

Besides,in Eq.(4),Fρππis the form factor of ρ0.In our present calculation we adopt the following form as used in previous works[41−45]

where Λρis the cutoff parameter of ρ0.

2.2 Decay Amplitude for the Triangular Loop

In addition to the tree level diagrams shown in Fig.1,we study also the contributions of ππ→ππ and K→ππ final state interaction(FSI).For this purpose,we use the triangular mechanism contained in the diagrams shown in Fig.2,consisting in the rescatering of the ππ and Kpairs.The rescattering of ππ and Kin coupled channels dynamically generates the f0(500)and f0(980)resonances.

Fig.2 Triangular loop contributions to the(1260)→ π+π−π+decay.

We can write explicitly the decay amplitudes for the triangular diagrams shown in Fig.2 as(see also Ref.[46],where more details can be found)

whereandare the meson-meson scattering amplitudes obtained in the chiral unitary approach in Ref.[47],which depend on the invariant mass of π+π−.The tππ→ππandin the first and second terms in Eqs.(9)and(10)depend onand,respectively.In addition,in Eq.(9)the quantities I1and I2are given by

3 Numerical Results and Discussion

With the decay amplitudes obtained above,we can easily get the total decay width of a1(1260)→ 3π which

with q the four-momentum of the a1(1260).Here we give explicitly the results for the tree diagrams,as an example,

With all the ingredients obtained above,one can easily get the total decay width of a1(1260)→ 3π by performing the integration of M12and cosθ∗.The results for Γ as a function of Λρis shown in Fig.3 with Ma1=1230 MeV.From Fig.3 one can see that the results for Γ are not sensitive to the value of Λρ,therefore,we fix Λρ=1500 MeV in the next calculations.

Fig.3 The total decay width of a1(1260)→ 3π as a function of the cutoff parameter Λρ.

Fig.4 The π+π− invariant mass distribution for a1(1260)→ 3π as a function of the invariant mass of the π+π− system.The experimental data are taken from Ref.[50].

However,since a1(1260)has large total decay width which should be taken into account.For this purpose we replace the dΓ in Eq.(15)by d:

In Fig.4,we show the numerical results for π+π−invariant mass distributions.We compare also our theoretical calculations with the experimental results of Ref.[50]measured in the decay of τ→ π−π−π+ντ.In Fig.4 we see that the tree level alone can describe well the experimental data around the ρ peak.This is attributed to the effect of the ρ0off shell propagator.The implementation of the

where the spectral function S(m2)is defined as contributions of the triangle loop diagrams is responsible for the enhancement of the invariant mass distribution at the lower invariant masses,where the f0(500)resonance appears.There is also a small peak around the Kmass threshold,where the f0(980)resonance appears.

Fig.5 The total decay width of a1(1260)→ 3π as a function of Ma1.

The numerical results in Fig.4 show how the most drastic change in the line shape of the the invariant π+π−mass distribution is caused by the tree diagram alone in Fig.1 and,as mentioned before,this is tied to the ρ0contribution,which appears at tree level because of the large coupling of a1(1260)to ρπ channel obtained in the chiral unitary approach.[6]

Next, we calculate the total decay width of(1260) → π+π+π−as a function of the mass of a1(1260).The numerical result is shown in Fig.5.The width rises rapidly with increasing Ma1in the mass range Ma1<1300 MeV,while it goes to flat when Ma1>1400 MeV.Besides,we get Γ=166 MeV at Ma1=1230 MeV.There is still no precise measurement about the(1260)→π+π+π−decay,we cannot compare our result with experiment.Note that the width Γa1≡ Γa01→π+π−π0was studied in Ref.[19],and Γa1=860 MeV was obtained at Ma1=1230 MeV.One can see that the theoretical result in Ref.[19]is much different with us.On the other hand,there are two peaks in the solid curve in Fig.5,which are attributed to the effect of the ππ → ππ and K→ππ final state interactions.We hope that the future experiments could test the model calculations.

So far we have assumed that the a1(1260)resonance is fully made from ρπ andK∗interaction.The pole position(−/2)is identified from the zero of the denominator of the scattering amplitudes in the complex plane,and the effective couplings ga1ρπand ga1K¯K∗are calculated from the residues of the scattering amplitudes at the complex pole.We know that the a1(1260)Breit-Wigner parameters,Ma1and Γa1,deviate from its pole parameters by a large amount and are reaction dependent.[1]On the other hand,we have no information on how the effective couplings obtained at the pole position change with varying Ma1,and therefore,we cannot include the uncertainties of these effective couplings without making further assumptions.Besides,there are hints that the a1(1260)resonance could have also other components as mention above,thus,there should be also contribution from a1(1260)→ f0(500)π → 3π[1]in the tree level.However,the information about this contribution is very scarce.We will leave such studies to a future work.

4 Summary

In this work,we evaluate the partial decay width of the(1260)→ π+π+π−with the assumption that the a1(1260)is dynamically generated from the coupled channel ρπ andK∗interactions.The dominant tree level diagrams that proceed via(1260)→ ρ0π+→ π+π+π−are considered.Besides,we also take into account the final state interactions of ππ → ππ and K→ ππ.It is found that the contributions from ππ → ππ and K→ππ are small compared to the tree level diagram,but they change the π+π−invariant mass distributions of the a1(1260)→ 3π decay.

The results that we obtained for the π+π−invariant mass distributions are in a fair agreement with the experimental measurements for the τ→ π−π−π+ντdecay.This provides new support for the molecular picture of a1(1260).Furthermore,we calculate also the total decay width as a function of the mass of a1(1260),it is found that our result is different with other model calculations.Thus,we hope that the further experimental observations of the π+π−and π+π+π−mass distributions would then test these model calculations and provide vary valuable information on the relevance of the ρπ component in the a1(1260)wave function.

[1]C.Patrignani,et al.,[Particle Data Group],Chin.Phys.C 40(2016)100001.

[2]E.Klempt and A.Zaitsev,Phys.Rep.454(2007)1.

[3]N.Brambilla,et al.,Eur.Phys.J.C 74(2014)2981.

[4]V.Baru,J.Haidenbauer,C.Hanhart,et al.,Phys.Lett.B 586(2004)53.

[5]T.Hyodo,D.Jido,and A.Hosaka,Phys.Rev.C 78(2008)025203.

[6]L.Roca,E.Oset,and J.Singh,Phys.Rev.D 72(2005)014002.

[7]L.Roca,A.Hosaka,and E.Oset,Phys.Lett.B 658(2007)17.

[8]H.Nagahiro,L.Roca,A.Hosaka,and E.Oset,Phys.Rev.D 79(2009)014015.

[9]C.B.Lang,L.Leskovec,D.Mohler,and S.Prelovsek,J.High Energy Phys.1404(2014)162.

[10]Y.Zhou,X.L.Ren,H.X.Chen,and L.S.Geng,Phys.Rev.D 90(2014)014020.

[11]M.F.M.Lutz,and E.E.Kolomeitsev,Nucl.Phys.A 730(2004)392.

[12]S.Weinberg,Phys.Rev.Lett.18(1967)507.

[13]C.W.Bernard,A.Duncan,J.LoSecco,and S.Weinberg,Phys.Rev.D 12(1975)792.

[14]G.Ecker,J.Gasser,A.Pich,and E.de Rafael,Nucl.Phys.B 321(1989)311.

[15]D.Gomez Dumm,A.Pich,and J.Portoles,Phys.Rev.D 69(2004)073002.

[16]M.Wagner and S.Leupold,Phys.Rev.D 78(2008)053001.

[17]D.G.Dumm,P.Roig,A.Pich,and J.Portoles,Phys.Lett.B 685(2010)158158.

[18]I.M.Nugent,T.Przedzinski,P.Roig,et al.,Phys.Rev.D 88(2013)093012.

[19]N.N.Achasov and A.A.Kozhevnikov,Phys.Rev.D 71(2005)034015.

[20]P.Lichard and J.Juran,Phys.Rev.D 76(2007)094030.

[21]C.Cheng,J.J.Xie,and X.Cao,Commun.Theor.Phys.66(2016)675.

[22]H.Nagahiro,K.Nawa,S.Ozaki,et al.,Phys.Rev.D 83(2011)111504.

[23]L.S.Geng,E.Oset,J.R.Pelaez,and L.Roca,Eur.Phys.J.A 39(2009)81.

[24]Z.H.Guo and J.A.Oller,Phys.Rev.D 93(2016)096001.

[25]M.Bando,T.Kugo,and K.Yamawaki,Phys.Rep.164(1988)217.

[26]N.Kaiser and U.G.Meißner,Nucl.Phys.A 519(1990)671.

[27]T.Sakai and S.Sugimoto,Prog.Theor.Phys.113(2005)843.

[28]T.Sakai and S.Sugimoto,Prog.Theor.Phys.114(2005)1083.

[29]M.Alekseev,et al.,[COMPASS Collaboration],Phys.Rev.Lett.104(2010)241803.

[30]D.M.Asner,et al.,[CLEO Collaboration],Phys.Rev.D 61(2000)012002.

[31]R.A.Briere,et al.,[CLEO Collaboration],Phys.Rev.Lett.90(2003)181802.

[32]T.E.Coan,et al.,[CLEO Collaboration],Phys.Rev.Lett.92(2004)232001.

[33]R.R.Akhmetshin,et al.,[CMD-2 Collaboration],Phys.Lett.B 466(1999)392.

[34]P.Salvini,et al.,[OBELIX Collaboration],Eur.Phys.J.C 35(2004)21.

[35]M.Bando,T.Kugo,S.Uehara,et al.,Phys.Rev.Lett.54(1985)1215.

[36]U.G.Meißner,Phys.Rep.161(1988)213.

[37]M.Harada and K.Yamawaki,Phys.Rep.381(2003)1.

[38]J.J.Xie,C.Wilkin,and B.S.Zou,Phys.Rev.C 77(2008)058202.

[39]H.C.Chiang,E.Oset,and L.C.Liu,Phys.Rev.C 44(1991)738.

[40]C.Hanhart,Y.S.Kalashnikova,and A.V.Nefediev,Phys.Rev.D 81(2010)094028.

[41]J.J.Xie,B.S.Zou,and H.C.Chiang,Phys.Rev.C 77(2008)015206.

[42]K.Tsushima,A.Sibirtsev,and A.W.Thomas,Phys.Rev.C 62(2000)064904.

[43]A.M.Gasparyan,J.Haidenbauer,C.Hanhart,and J.Speth,Phys.Rev.C 68(2003)045207.

[44]J.J.Xie and B.S.Zou,Phys.Lett.B 649(2007)405.

[45]J.J.Xie,Phys.Rev.C 92(2015)065203.

[46]F.Aceti,L.R.Dai,and E.Oset,Phys.Rev.D 94(2016)096015.

[47]J.A.Oller and E.Oset,Nucl.Phys.A 620(1997)438,Erratum:[Nucl.Phys.A 652(1999)407].

[48]F.Aceti,J.M.Dias,and E.Oset,Eur.Phys.J.A 51(2015)48.

[49]F.Aceti,J.J.Xie,and E.Oset,Phys.Lett.B 750(2015)609.

[50]H.Albrecht,et al.,[ARGUS Collaboration],Z.Phys.C 58(1993)61.