大学生COVID-19认知数据回归分析

段萱健， 徐平峰

(长春工业大学 数学与统计学院，吉林 长春 130012)

0 引 言

2019年12月以来，新型冠状病毒肺炎(Corona Virus Disease 2019，COVID-19)爆发，目前已在全球范围内蔓延，对世界各国都造成了很大影响，各国都采取了严厉措施限制其传播。COVID-19临床表现，从无症状或缺乏症状形式，到伴有呼吸衰竭的严重病毒性肺炎、脓毒症和感染性休克的多器官和全身功能障碍，以及死亡。因此对于大学生来说，找到影响学生COVID-19认知的原因是十分必要的。

王福友等[1]用SIS方法结合Lasso变量选择方法建立了Logistic回归模型，通过AIC、BIC准则以及交叉验证(CV)对基因表达数据进行了变量选择。

文中下载了印度尼西亚大学生对COVID-19相关知识考察的数据[2]，由于数据中自变量是分组变量，响应变量是多分类变量，因此,我们考虑结合Group Lasso惩罚似然方法和逐步回归方法建立多类别logistic回归模型，使用不同的模型方法选择出最优模型。分析大学生对于新冠肺炎的知识了解情况，旨在更好地预防、遏制COVID-19的传播，帮助学生正确认识COVID-19，理解且重视学校的各项防疫措施，做好心理防护，同时，协助学校进行管理、规划教育、干预学生的认知。

1 多类别logistic回归

多类别logistics回归[3]将多分类响应变量与解释变量联系起来，是应用最广泛的回归模型。考虑一个多分类响应变量Y，具有K个类别，x=(x1,x2,…,xp)为解释变量。给定数据集(xi,yi)，xi=(xi1,xi2,…,xip)，yi∈{1,2,…,K}，i=1,2,…,N，参照文献[4]，多类别logistic回归模型一般形式如下

(1)

式中：β0l——参数的截距项,βl=(β1l,β2l,…,βpl),l=1,2，…,K。

对于参数的可识别性，可以通过正则化解决，即有如下约束条件

βK=0，

(2)

式中：K——参照类别。

2 方法介绍

2.1 Group Lasso惩罚似然方法

Group Lasso惩罚由Yuan M等[5]在2006年提出，参照文献[6]，文中将其写为如下形式

(3)

式中:γJ——组权重,γJ∈[0,∞),J=1,2，…,m;

β(J)——参数β的第J块,β=(β1,β2,…,βK-1)T。

多类别logistic回归的对数似然为

(4)

式中:M1=I(yi=l|xi);

Group Lasso惩罚的极大似然估计，也就是估计惩罚负对数似然的最小值

(5)

式中：r——第J组中的变量个数,J=1,2，…,m;

λ——调节参数,λ≥0。

2.2 逐步回归方法

逐步回归[7]的基本思路是从自变量中选取重要的变量，建立回归分析的预测或者解释模型。基本步骤是将自变量逐个引入或剔除，计算对应的模型AIC值或BIC值，通过这样引入剔除变量的过程，选取这个过程中AIC值或BIC值最小的模型作为最优模型。

3 COVID-19认知数据实证分析

3.1 数据描述

文中引用数据为印度尼西亚大学生对COVID-19相关知识、态度和实践调查数据[2]的部分数据,包括社会人口信息(6个变量)、知识问卷(18个问题)、态度问卷(6个问题)和实践问卷(12个问题)。文中使用其中的社会人口信息数据和知识问卷的数据。问卷有效标准为答卷人满足：

1)本科生；

2)健康，无COVID-19；

3)从未患过COVID-19。

该调查共收到6 252份回复，但有3份回复由于标准未被满足而被消除，因此共回收有效问卷6 249份。知识问卷的18个问题测试了COVID-19相关知识，包括病因、症状、风险群体、传播和预防。对于知识问卷的每个问题，回答正确计1分，不正确计0分。我们计算出每名学生知识问卷的总分，进行离散化处理，分为优秀、良好、一般三类，一般记为1，良好记为2，优秀记为3，将其作为响应变量。社会人口信息的6个变量分别为性别、年龄、现居住地、入学时长、专业、职业。将这6个变量作为自变量，将其转化为哑变量分别记为x1，x2，…，x10。其中第一组变量为x1，第二组变量为x2，第三组变量为x3，第四组变量为x4、x5、x6、x7，第五组变量为x8、x9，第六组变量为x10。

参与者社会人口的统计信息和具体的变量取值及分组说明见表1。

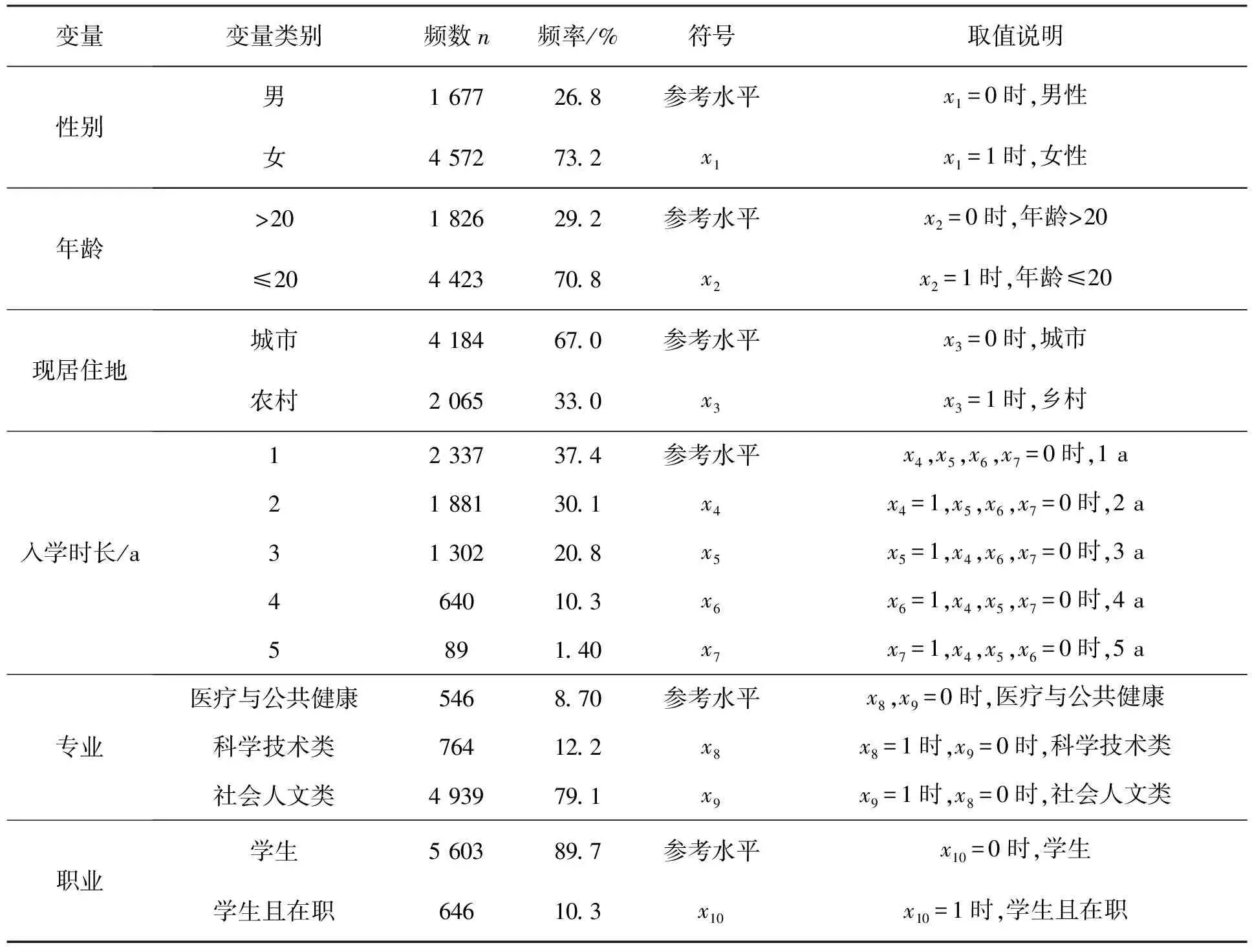
表1 参与者的社会人口信息(n=6 249)

3.2 结果分析

文中选取的评价指标为精度(Accuracy，ACC)[8]，即

利用GroupLasso惩罚对数似然方法，在训练集上训练模型，结合AIC、BIC准则和10折交叉验证法(CV)选出最优模型，在测试集上计算模型拟合精度。在R软件中，应用R包msgl来实现这个过程，结果见表2。

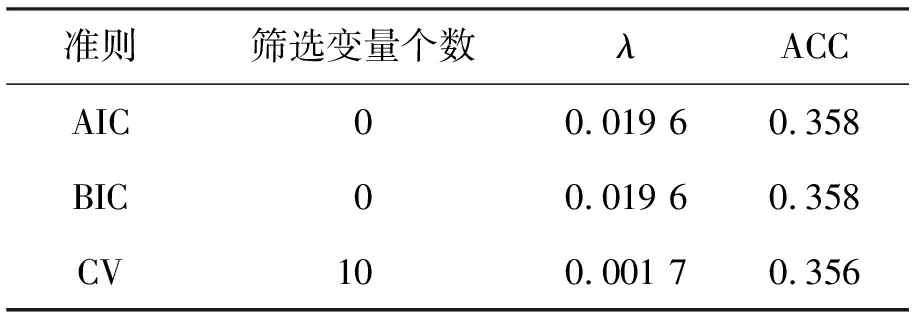
表2 Group Lasso惩罚对数似然方法在不同准则下选择的结果

BIC值和AIC值变化分别如图1和图2所示。

图1 BIC值变化

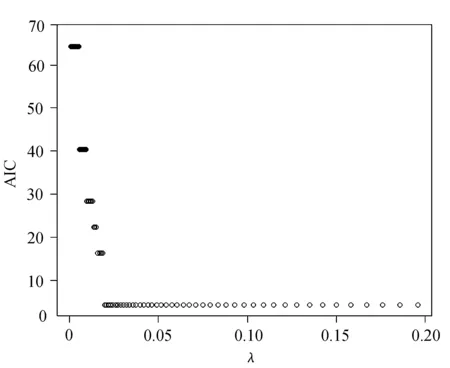
图2 AIC值变化

由图1和图2可以看出，在实际计算过程中，随着λ值的增加，AIC值与BIC值都呈现出单调递减并趋于某一值的趋势。从表2中可以看出，AIC准则和BIC准则选取了相同的模型，且选择的模型为空模型，因此，应用AIC准则和BIC准则对该模型进行选择的结果并不理想。三种模型选择方法下的模型精度分别为0.358、0.358和0.356,都比较低，说明模型拟合效果一般。

基于文中研究数据，考虑有三种原因导致模型精度较低：

1)Group Lasso惩罚对数似然的多类别logistic回归模型不适用于文中研究的数据集；

2)模型选择的方法不适用于Group Lasso惩罚对数似然的多类别logistic回归模型；

3)未考虑到变量序的影响。

利用逐步回归的变量选择方法在训练集上训练模型，结合AIC准则和BIC准则选择最优模型，在测试集上计算模型的精度。在R软件中，应用R包stats中的step函数和R包nnet中的multinom函数来实现这个过程。

逐步回归方法在不同准则下选择的结果见表3。

表3 逐步回归方法在不同准则下选择的结果

在5种最终模型的参数估计都通过检验的情况下，显然BIC准则下的多类别逐步logistic回归的精度最高，选择变量最少，即应用逐步回归+BIC准则得到的多类别Logistic回归模型为基于大学生COVID-19认知数据的最优模型，即：

p1(xi)=1-p2(xi)-p3(xi)。

BIC准则下的多分类逐步logistic回归模型结果见表4。

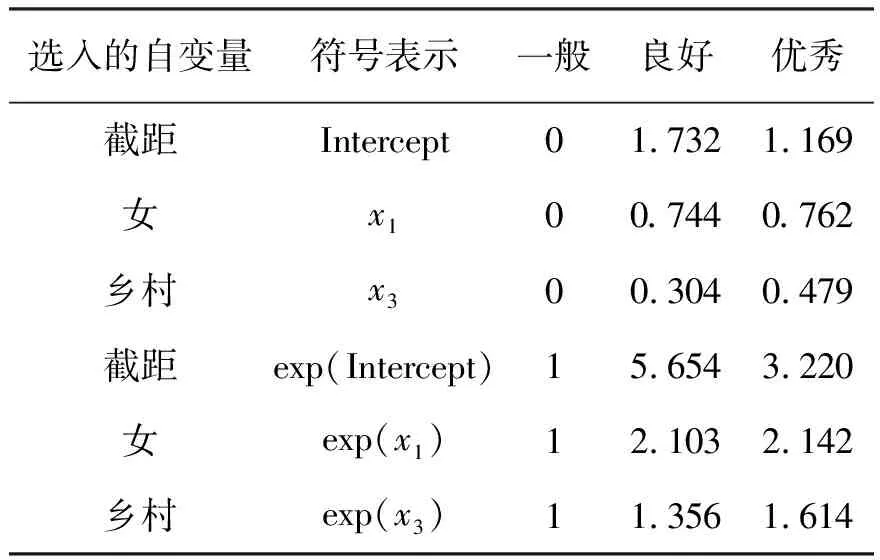
表4 BIC准则下的多类别逐步logistic回归模型结果(参照类别：一般)

由表4可以看出，影响大学生对于COVID-19认知的因素主要为性别与现居住地。对于性别，与参考类别男性相比，女性的COVID-19知识水平倾向于优秀。对于现居住地，与参考类别城市相比，居住在乡村的学生知识水平倾向于优秀。

4 结 语

基于印度尼西亚大学生对于COVID-19的认知数据，首先建立了多类别logistic回归模型，其次分别使用Group Lasso惩罚对数似然和逐步回归两种变量选择方法，利用AIC、BIC准则和交叉验证三种方法选择出最优模型为应用逐步回归 + BIC准则得到的多类别Logistic回归模型，最后结合最优模型的结果分析了影响学生对COVID-19知识掌握情况的因素。