模糊卡尔曼滤波北斗伪距定位

曹学瑶， 胡黄水， 韩 博

(长春工业大学 计算机科学与工程学院，吉林 长春 130012)

0 引 言

北斗卫星导航系统(以下称为北斗系统)是我国自主创建研发的卫星导航系统，也是全球第三个成熟的导航系统。在交通运输、农业林业、水力监测等领域都得到了普遍应用[1-2]。由于北斗系统可以为用户端提供全天候、全天时的高精度定位服务，所以提高北斗定位精度极其重要。

根据观测量的不同，北斗定位可以分为伪距定位和载波相位定位[3]。相比载波相位定位来说,伪距定位不要求高强度信号，也不存在整周模糊度的问题,并且伪距定位速度较快[4]。随着定位技术的日渐成熟，国内外专家对伪距定位算法展开了深入研究，目前的主流算法有极大似然估计、最小二乘法、卡尔曼滤波和牛顿迭代法等。文献[5]提出加权最小二乘法，对可信度高的观测值分配大的权值。但加权最小二乘法对观测数据中的粗差不具备处理能力，所以定位误差大。文献[6]采用抗差M估计算法，将最小二乘算法的解作为抗差初值，然后,根据伪距残差矢量和等价权矩阵进行计算位置坐标。和最小二乘法相比，抗差M估计定位精度更高。文献[7]采用卡尔曼滤波进行定位，直接将位置与钟差的信息作为状态变量求解,忽略了卡尔曼滤波对定位的初始位置敏感的特点，导致了定位精度不高。文献[8]提出在扩展卡尔曼滤波的基础上加入加权最小二乘法。首先,利用加权最小二乘法对系统进行线性化处理后,用扩展卡尔曼滤波对用户端位置进行预测。该算法相对于文献[7]提升了线性化的精度，但由于观测量中粗差和卡尔曼滤波中量测噪声固定不变的影响，难以满足高精度定位要求。

为了解决最小二乘法对观测数据中的粗差无法进行处理,以及卡尔曼滤波对初始位置敏感且量测噪声方差不变的问题，提出融合抗差M估计和模糊卡尔曼滤波算法进行伪距定位。首先,利用抗差M估计解算出用户端的位置，然后将解算结果作为卡尔曼滤波的初始状态位置,根据模糊控制系统不断调节滤波增益Kk值进行定位解算，从而提高定位精度。

1 伪距定位原理

伪距定位原理是通过北斗导航系统中导航卫星的三维位置坐标信息,以及卫星到接收端的距离得到用户端的三维位置坐标信息的过程[9]。其中,导航卫星的三维位置坐标信息可以通过导航电文中的星历数据获得，由于卫星发射的信号会受到各种误差的干扰,导致用户端接收到的观测距离并不准确。将带有误差的观测距离称为伪距[10],公式如下：

ρi=ri+δρ1+δρ2+c(δtu-δt1)，

(1)

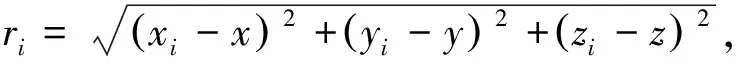
(2)

式中:ri——第i颗卫星与用户端的真实距离：

ρi——卫星与用户设备之间的真实距离；

δtu——电流层的时延距离；

δρ1——对流层的时延距离；

δt1——用户设备的钟差；

δρ2——卫星的钟差；

c——信号的传播速度,c=2.997 924 58 m/s;

(xi,yi,zi)——第i颗卫星的三维坐标；

(x,y,z)——用户接收机的位置坐标。

忽略可修正项，伪距定位公式为

ρi=ri+c(δtu-δt1)=

cδt,

(3)

i=1,2,…,n，

式中：δt——接收机的钟差。

2 算法设计

利用抗差M估计构造等价权函数，避免粗差影响未知参数的估值。将该估值作为模糊卡尔曼滤波器的初始值，并对量测噪声方差实时进行调整，进而提高系统的定位精度。

2.1 抗差M估计计算初值

在北斗导航系统中，最小二乘法是伪距定位系统的观测方程。初始值

x0=(x0,y0,z0,δt0)

处线性化后得到的系统观测模型为

Δy=H·Δx+e,

(4)

式中：Δx——m×1的矢量，表示状态残差，即真实位置与初始化后得到的位置之间的差值;

m——当前历元下的卫星个数;

Δy——m×1的矢量，表示伪距残差,即伪距的观测值与估计值之间的差值；

H——m×4的观测矩阵；

e——m×1的误差矢量，其元素一般假设为相互独立的高斯随机过程。

首先用最小二乘法解算此线性方程，目标函数为

(5)

初始值处的最小二乘解为

(6)

伪距残差矢量为

Δr=Δy-HΔx=(In-H(HTH)-1HT)e。

(7)

当测量噪声为高斯分布时，最小二乘估计为最优估计[11-13]。但在北斗导航系统中，观测量中含有粗差会直接影响最小二乘定位精度，因此采用M估计抑制粗差[14]，其目标函数为

(8)

(9)

采用Huber[15]函数给含有粗差的观测值赋予小的权值

(10)

式中:k——根据M估计方差性能确定的常数。

抗差M估计表达式为

(11)

式中：Wk+1——等价权矩阵，公式为

(12)

抗差M估计定位的具体步骤为：

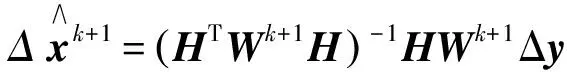
4)返回2)，直到两相邻步骤的回归系数差值小于设定阈值时，迭代结束，即

max|xk+1-xk|<ξ。

2.2 模糊自适应Kalmen滤波定位

扩展卡尔曼滤波有两个系统模型[16]：系统观测模型以及系统状态模型。

状态方程

xk=Ak,k-1xk-1+ωk-1,

(13)

式中：xk——历元k下的系统状态向量；

xk-1——历元k-1下的系统状态向量;

Ak,k-1——历元k-1到历元k的状态转移矩阵;

ωk-1——高斯白噪声，均值为零，且相互独立。

观测方程

yk=Bkxk+vk,

(14)

式中：yk——历元k的观测量；

Bk——状态量和观测量之间的关系矩阵；

vk——高斯白噪声，均值为零，且相互独立。

扩展卡尔曼滤波包含预测和更新两个过程[16-17]，其预测方程为：

状态先验估计值

(15)

求解先验估计值的协方差

(16)

式中：Qk——系统噪声序列的方差阵。

其更新方程为：

滤波增益矩阵

(17)

式中：Rk——测量噪声序列的方差阵。

对状态更新

(18)

对协方差阵更新

(19)

量测噪声具有随机性[18],但扩展卡尔曼滤波中量测噪声的方差始终都采用初始计算时的先验值[19],因此,采用模糊卡尔曼滤波[17]调整量测噪声的协方差矩阵[20]来减小滤波发散。

新息(rk)是观测量估计值与观测量真实值的差，公式为

rk=yk-Bkxk,k-1。

(20)

式(18)可以写为

(21)

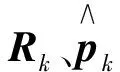
(22)

(23)

由模糊推理系统(FIS)可以计算出调整因子tk。tk可以对量测噪声方差进行调整。模糊推理系统[21]采用单输入、单输出Mamdani模糊逻辑控制器[22]，将每一步的残差实测方差与理论方差的比值作为输入，输出为tk。采用的隶属度函数如图1所示。

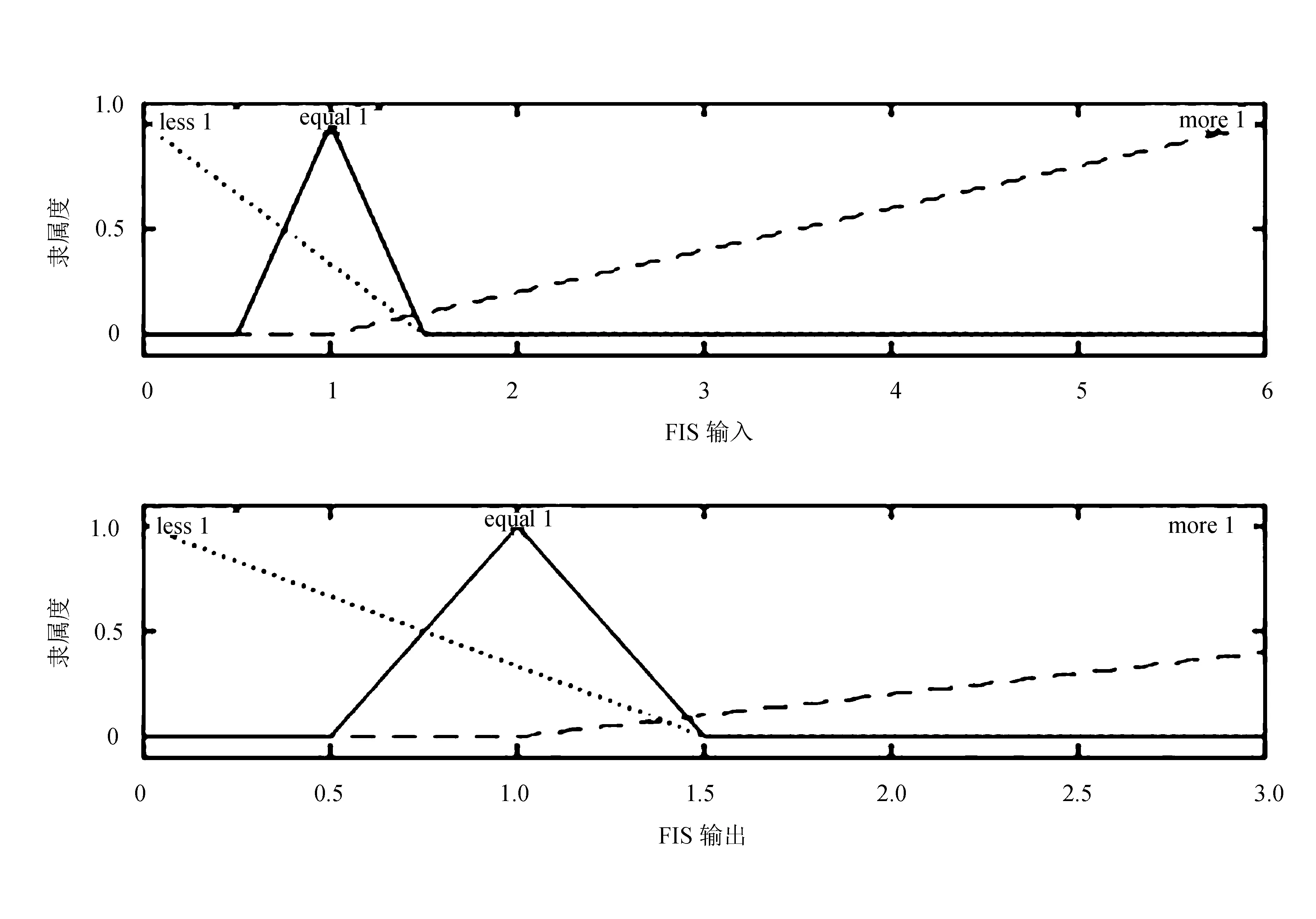
图1 Ck与tk的隶属度函数

模糊规则为：

If1>,then1>

If,then

If,then

Fk残差的实测方差阵受新息影响,

(24)

式中：N——统计数。

Dk是残差的理论方差阵，

(25)

Ck是残差的实测方差矩阵和残差的理论方差矩阵的商,

(26)

每进行一次滤波FIS更新一次输出值,即tk，再将tk代入式(22)、式(23)中,对量测噪声方差矩阵进行在线调整。

因此,基于M估计的模糊卡尔曼滤波定位解算步骤如下:

1)将M估计解算位置和钟差信息作为扩展卡尔曼滤波的状态初始值，然后初始化协方差阵;

2)建立模糊卡尔曼滤波系统方程，对状态向量和观测向量协方差阵进行估计。通过FIS计算调整因子tk，然后进行预测和更新过程;

3)判断历元是否解算完毕，未完成返回2),继续解算。

3 仿真分析

采用Matlab软件对RINEX文件数据[23]进行解算。在观测文件为 450个历元数据的情况下，分别采用扩展卡尔曼滤波,以及模糊自适应卡尔曼滤波方法对X、Y、Z三 个方向进行解算，然后再将定位结果进行对比分析。误差对比如图2所示。

(a)扩展卡尔曼滤波算法在X、Y、Z三个方向的误差结果

图2中,X、Y、Z三个方向的平均误差分别为-3.96、-8.96、-13.47 m，明显可以看出，模糊卡尔曼滤波算法的误差更小，滤波结果也更加平滑。模糊卡尔曼滤波的定位解算结果相较于扩展卡尔曼滤波的定位精度有明显提高，相较于图2(a)的收敛过程也明显缩短，实现了更加精确的定位。

利用Matlab软件将扩展卡尔曼滤波与模糊卡尔曼滤波的运动轨迹与接收机真实轨迹进行模拟。

将扩展卡尔曼滤波、真实轨迹以及模糊卡尔曼滤波进行误差对比，如图3所示。

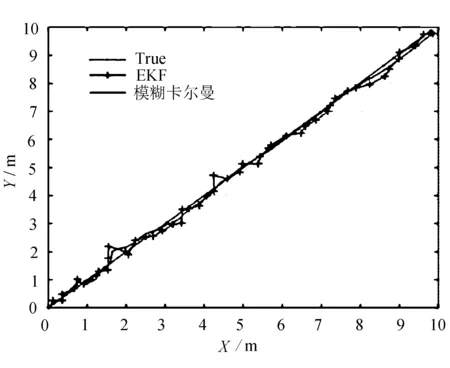
图3 扩展卡尔曼滤波、真实轨迹以及模糊卡尔曼滤波误差对比

由图3可以看出，扩展卡尔曼滤波与真实值之间存在的误差较大,且拟合度不高; 而模糊卡尔曼滤波运动轨迹更加集中，而且均匀分布在真实轨迹四周，拟合程度较好。故模糊卡尔曼滤波对定位误差具有极好的改进。

4 结 语

结合M估计和模糊卡尔曼滤波的定位解算算法，将抗差M估计的定位结果作为扩展卡尔曼滤波算法的初值，通过模糊推理系统得到的调整因子来调整量测噪声抑制滤波发散情况，进而提高定位精度。解决了传统最小二乘算法对粗差不具抵抗力，以及卡尔曼滤波收敛过程慢且对初值敏感的缺点。

通过 Matlab 处理数据的实验结果也表明，模糊卡尔曼滤波算法的收敛速度与定位精度均明显提高。