测试系统分析在质量控制中的应用

陈典斌，韩东霏，马 杰，马俊英

（中国人民解放军63850 部队，吉林白城 137001）

0 引言

随着科技现代化程度的不断提高，处于传统质量控制[1-3]下的实验室装备中各系统、设备长期服役，其质量影响因素呈现增长局面。为有效遏制实验过程中出现的质量问题、进一步提升质量监督效率，向多元过程的质量控制转变具有重要的理论意义和工程价值。以实验室所用系统设备作为研究分析对象，以精益六西格玛[4-6]为工具开展质量控制活动。

1 管理概念

ISO 9001 是国际标准化组织制定的国际标准，精益六西格玛（6σ）[7-9]是一种持续改进的方法，两者有明显的区别。ISO 9001力求建立规范化的质量管理体系，不太关注质量的经济性，强调全员参与，但部门和个人职责范围狭小，可以说它是一种接近于及格的评价。六西格玛是自发追求卓越的行为，没有终点，其本身就是一种质量改进的方法，与项目管理结合紧密，并广泛采用各种数据统计工具，更强调具体的统计技术应用。

2 应用分析意义

设备经过长期使用，不但性能可能会下降，人员操作差异性大也可能导致数据误测。对设备进行数据分析，不但可以评估实验室系统设备的稳定性，还能提前发现设备在运行过程中可能存在的问题，是过程质量管理的完善方向。通过持续不断的培训和各部门的互相协作，对技术指标进行量化和分析，验证实验人员的判断，从而避免错误分析掩盖实际应用问题，避免解决问题凭经验、凭直觉或想当然。精益六西格玛可用于装备保障、战场环境和特种作战环境中等复杂多变的应用中。

3 维修概率

电蒸汽发生器设备连续长期工作，会引发其相关部件出现各种不同的故障。若系统首次发生故障的时间T（单位h）服从指数分布E（0.002 5）：

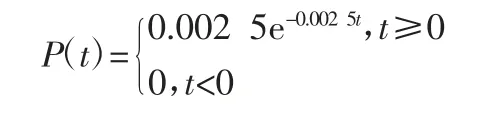
概率密度函数曲线如图1 所示。若对锅炉在连续工作100 h以内、200～400 h、500 h 以后需要维修的概率进行预测，锅炉在不同工作时间情况下的维修概率通过计算可得到，即锅炉在100 h 以内的维修概率为22.1%，在200～400 h 的维修概率为23.9%，500 h 以后需要维修的概率是28.7%。

图1 指数分布E（0.002 5）的概率密度曲线及指数分布分析结果

4 数据一致性分析

测量系统分析中一致性问题是研究数据质量问题的切入点。量化一致性测量指标和选择合适的测量函数来计算指标值的过程是十分复杂的，分别以结合测量系统的分析与生产过程的波动，以及先不考虑生产过程的波动这两种方法进行分析。

4.1 测量精确度

实验时需要对数据进行统计和计算。实际实验过程中，除了电子系统进行测量外，也常用人工对数据进行测量记录。实际操作过程中，数据会受到温度、湿度、压力、人员、部件等多个因素的影响，在分析过程中，不应该轻易排除任意一个影响因素。

对这种具有重复性和再现性的数据进行测量和整理，考察测量过程是否稳定，同时为简化计算，只计算和分析了人员和部件两个变异因素。测量系统分析时，选择A、B、C 三个操作者，对8 个测量量筒进行数据记录，波动源方差分析和测量系统能力的计算结果如图2 所示。

图2 试验数据重复性与再现性分析

采集数据分析计算结果：重复性方差为2.437 5，检验员方差为1.150 3，检验员与量筒交互作用方差为3.339 3，再线性方差为2.118 86，重复性方差与再现性方差求和（）为4.556 36，过程方差为23.166 7，的值为30.093 8。计算可得到：Gage R&R=47.98%＞10%，P/T=1579.16，可见重复性和再现性的水平都不高；ndc=2＜5，可见分辨力较弱。总之，测量系统不合格，需再次评估。

4.2 无波动测量分析

加速腐蚀实验需判定被试品表面腐蚀缺陷情况。测厚仪测量被试品表面膜层厚度和公差是，标准差σp=。选用一组固定被试品，在12 h、24 h 和48 h 三个不同时刻各进行装上/卸下3 次循环，每次循环中重复测量3 次膜厚，进行测量系统分析（图3）。

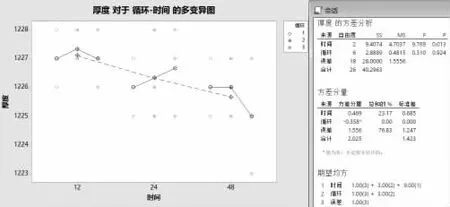
图3 测量系统固定件多变异图及方差分析

从图3 及数据结果可以看出，循环的影响似乎不大，但时间影响显著。方差分析计算可得到P/T=10，Cp=0.75。两项指标都没有达到合格标准，说明过程能力较差，因为该指标是过程的关键指标，因而测量系统必须改进。

5 结束语

测量系统分析对提高质量至关重要。本文针对实验中的设备维修、数据处理和实验结果3 个方面的问题，使用Minitab 数据统计分析软件进行了系统分析，保证输出真实有效的实验室统计数据结果，使测量具有可控性，切实提高了保障效率，保证实验可靠性。