基于新阈值函数的小波去噪研究

赵淑君 农林舒真 黄晓文 寇俊克*

（桂林电子科技大学数学与计算科学学院,广西 桂林541004）

在实际应用中,获取的信号通常含有噪声。这一现象的产生一方面是由于采集信号数据时容易受到外部杂音的影响,使得信号数据含有噪声。另一方面原因在于信号采集设备的技术设计缺陷等,比如设备的数据精度、灵敏度等技术限制。噪声的存在不仅影响信号的质量,严重时还会淹没原始信号。因此,信号去噪研究是信号处理领域中的基本研究问题[1-2]。小波作为“数字显微镜”,以其独特的局部时频分析特性而被广泛应用于信号去噪[3-5]。经典小波阈值去噪研究起源于Donoho[6]的工作,他依据小波信号分解特征提出了软、硬阈值函数去噪算法,并取得了较好的去噪效果。然而,常规软、硬阈值函数在数学表达式上存在一些缺陷,比如硬阈值函数在阈值处不连续,软阈值函数在阈值处不可导。这些数学性质方面的不足可能会导致常规阈值函数进行信号去噪处理时出现边缘模糊,甚至会出现信号部分失真的现象。为了克服常规软硬阈值函数的上述缺点,牟雪姣等[7]借助圆切线的相关理论原理,提出了一种新的阈值函数,提高了非平稳信号的去噪效果。李维松等[8]针对小波阈值去噪算法中的阈值函数及阈值选取准则进行了改进完善,并选取Heavysine 信号以及Block 信号进行去噪效果验证。为了最大程度上提高去噪效果,2021 年李树勋等人[9]根据指数函数特性,在硬阈值函数的基础上提出了一种改进的阈值函数,并通过仿真实验验证了改进阈值函数具有更优的去噪效果。然而,上述改进阈值函数没有考虑大于阈值的小波系数处理问题,这就意味着该阈值函数并非最优。基于此,本文将从数学表达式以及去噪实效两方面分析常规软、硬阈值函数、改进阈值函数的优缺点,引入平滑因子构建一种新的阈值函数。同时,选取两组具有不同特征的信号进行去噪仿真实验,通过误差分析对比发现新阈值函数具有更好的去噪效果。

1 小波阈值去噪

信号去噪的数学模型为

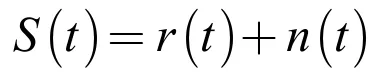
其中,S(t)为含噪声信号,r(t)为原始信号,n(t)为噪声。信号去噪的目的是尽可能的减少噪声n(t)对S(t)的影响,进而获得真实信号r(t)。在小波去噪过程中,含噪声信号经过小波分解以后,信号的能量将会集中在一些幅值较大的小波系数上。相反地,噪声能量则会分布在整个小波域,这就意味着幅值较小的小波系数很大程度上以噪声为主。基于这一特点,一般情况下默认幅值较大的小波系数为信号,而幅值较小的小波系数为噪声。借助小波上述去相关性特征,小波在信号处理、图像处理、数据分析与预测等[7-11]方面发挥着极其重要的作用。下面简单介绍一下小波变换的相关定义。一维连续函数r(t)的连续小波变换为：

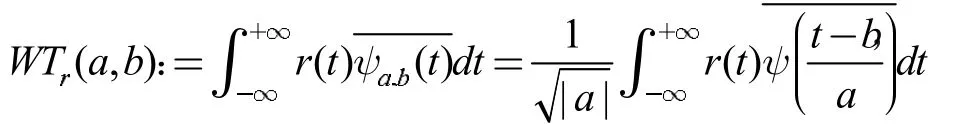
其中,WTr(a,b) 为相应的小波系数,ψa,b(t)是小波函数,ψ(t)为基本小波,a 是伸缩因子,b是平移因子。另一方面,小波逆变换为

下面简要叙述一下小波阈值去噪的关键步骤：

(1) 分析含噪声信号特性,选择合适的小波函数以及分解层数进行小波分解,获得不同尺度参数下的小波系数Wj,k。

(2) 借助适切的阈值函数以及阈值参数,对获取的小波系数进行阈值处理。

(3) 针对上述阈值算法处理后的小波系数进行小波重构,进而获得去噪信号。

2 新阈值函数

纵观小波阈值算法,阈值函数在去噪结果中发挥着决定性作用。下面我们将给出常规软、硬阈值函数的定义,并分析其优缺点。

这里,Wj,k为含噪声信号经过小波分解后得到的小波系数j,k是阈值算法处理后的小波系数, λ为阈值。其常规阈值函数图像如图1 所示。

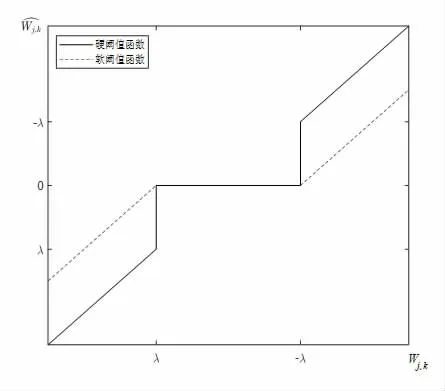
图1 软、硬阈值函数图像

通过阈值函数表达式可以看出,当小波系数绝对值小于阈值时,常规阈值函数都是直接将其变为零,这一处理方法在很大程度上可以有效地去除噪声。同时,硬阈值函数只关注于较小的小波系数,这意味着硬阈值函数能够保留原始信号更多的细节特征。然而,硬阈值函数在阈值处是不连续的,这会使得去噪处理后的信号产生局部抖动现象。对于软阈值函数来说,该阈值函数整体上具有良好的连续性,所以利用软阈值函数去噪处理后的信号较为平滑。但是,软阈值函数算法中小波系数存在恒定偏差,进而导致信号去噪精度不高,甚至出现失真的现象。针对传统软、硬阈值函数的不足,李树勋等[9]提出利用指数函数的衰减特性,结合硬阈值函数,通过在指数函数中加入参数来调整阈值函数的陡峭性,进而构造了一种改进的阈值函数,

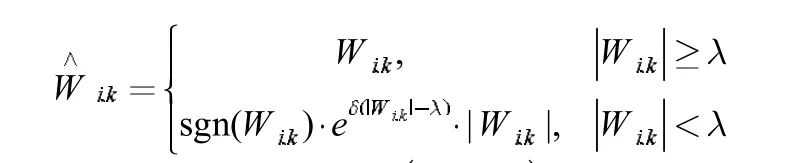
其中,λ 为阈值, δ （δ ＞0）为调节因子。其函数图像如图2 所示。

图2 文献[9]阈值函数图像

上述改进阈值函数通过结合硬阈值函数与指数函数,使得与阈值接近的一部分小波系数能够被保留,防止了对信号的过度去噪,取得了较好的去噪效果。需要指出的是,当小波系数绝对值大于阈值时,虽然小波系数主要以原始信号为主,但是也有可能含有部分噪声。为了达到更加理想的去噪效果,必须改进完善硬阈值函数的处理方法,使其尽可能最大程度上消除噪声。

通过上述关于常规软、硬阈值函数特性分析,为了取得更优的去噪效果,本文继承了常规阈值函数的优势,在文献[9]阈值函数的基础上提出了一种新的阈值函数,

这里,α 为新引进的平滑因子。当 α增大时,新阈值函数越来越接近于硬阈值函数。当 α减小时,新阈值函数则变得更加平缓。众所周知,硬阈值函数在信号去噪处理中可以较好地保留原始信号的细节特征,这就意味着硬阈值处理后的信号不够光滑。基于这一特征,在借助上述新阈值函数进行信号去噪处理时,如果要保留更多的细节特征,则平滑参数α 可适当增大；若期望得到较为光滑的去噪信号,可以通过减小平滑参数实现。通过上述分析可以得出,新阈值函数的去噪效果一定程度上也依赖于平滑因子的取值。下面给出新阈值函数(α=0.9)与其他几种阈值函数的对比图像。

图3 新阈值函数与文献[9]阈值函数、硬阈值函数、软阈值函数图像对比

从数学表达式以及图像可以看出：新阈值函数在(- ∞, +∞)是连续的；新阈值函数是以y=x 为渐近线的,即随着Wj,k增 大,小波系数j,k越来越接近于原始系数Wj,k。同时,新阈值函数在形式上也越来越趋近于常规硬阈值函数。综上所述,新阈值函数通过引入平滑因子对阈值函数进行重新构造,改进了其对于大于阈值的小波系数的处理方式,理论上提升了信号的去噪质量。新阈值函数在定义域上是连续的,避免了去噪过程中伪吉布斯现象的出现。此外,新阈值函数在接近阈值部分对小波系数进行减弱处理,在远离阈值部分十分接近硬阈值函数,尽可能保留了信号的有效部分。同时,利用新阈值函数进行信号去噪处理时,可以通过调整平滑参数进行去噪效果优化,这一特点使得新阈值函数就有更强的适应性。

3 仿真实验

为了验证本文所提新阈值函数的有效性,借助MATLAB 软件进行信号去噪仿真实验。选取Doppler 信号,添加噪声强度为26dB 的随机噪声。在小波阈值算法中小波函数选用sym8 小波,分解层数为5,平滑因子α取值2.36,其去噪结果如图4、表1 所示。通过观察图4可以看出,本文所选Doppler 信号具有非平稳特性,该信号的振荡频率逐步由强变弱,且前端部分振荡极强,故针对此信号的去噪处理具有一定的难度和代表性。

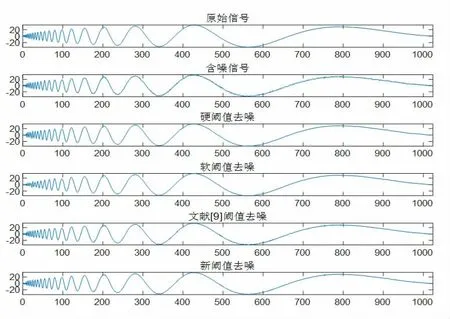
图4 Doppler 信号去噪结果

表1 信噪比和均方根误差对比表

由图4 可以看出,上述四种阈值函数均可以有效地消除噪声。另外,信噪比作为衡量信号去噪效果的关键指标之一,其信噪比数值越大,表示信号去噪效果越好。均方根误差旨在度量去噪处理后的信号与原始信号的差距,即均方根误差越小,则去噪处理后的信号越接近于原始信号,去噪效果越好。利用表1 中数据对比常规软、硬阈值函数、文献[9]阈值函数、新阈值函数的去噪信噪比以及均方根误差可以看出,新阈值函数去噪效果最好。为了验证新阈值函数的一般性,下面采用quadchirp 信号进行处理,添加噪声强度为19dB 的随机噪声,同样选取sym8 小波函数,分解层数为5,平滑因子取值1.7,其结果如图5、表2 所示。通过观察图5 可以发现,本文所选Doppler 信号以及quadchirp 信号均为非平稳信号。Doppler 信号的振荡频率为由强逐渐变弱,而quadchirp 信号的振荡特性则为由弱变强。特别地,从图5 还可以看出本文所选的quadchirp 信号在后端部分振荡频率极高。众所周知,噪声之所以称之为噪声,主要是由于噪声相对于原始信号来说具有更高的频率,也就是振荡频率较高。然而,本文所选的quadchirp 信号在后端具有极高的振荡频率,这一点在形式上与噪声特征一致,这就大大增加了信号去噪的难度。但是,需要特别说明的是,从下述去噪实验结果可以得出即使针对具有噪声特征的含噪声信号,本文所提出的新阈值函数仍然具有较好的去噪性能。

图5 Quadchirp 信号去噪效果

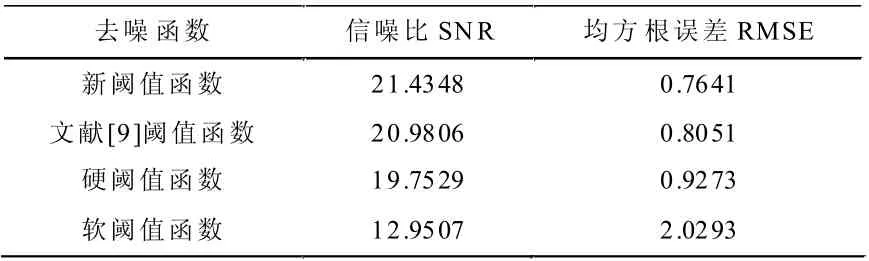
表2 信噪比和均方误差的对比表

通过观察图5 容易看出,常规阈值函数、文献[9]阈值函数、新阈值函数都达到了有效去除噪声的目的。然而,从表2误差分析可以得出,新阈值函数相对于其他阈值函数具有更高的信噪比,且均方根误差最小,这就表明了新阈值函数具有更好的去噪效果。

结束语

本文基于小波阈值去噪基本原理,通过分析传统阈值函数和其他改进阈值函数的特点,提出了一种新阈值函数。新阈值函数不仅保持了常规软、硬阈值函数的优点,同时又克服上述改进阈值函数的不足。仿真实验结果表明：新阈值函数相对于其他阈值函数去噪效果更加明显,具有较强的去噪优势。