火箭炮底架多目标优化设计
焦阿允,马新谋,李魁武
(1.中北大学 机电工程学院,山西 太原 030051;2.中北大学 军民融合协同创新研究院,山西 太原 030051)
防空火箭炮具有灵活机动、成本低廉、火力猛烈的特点,可有效地填补防空导弹和防空高炮的火力间隙,对低空目标实施有效毁歼[1]。火箭炮底架是由薄厚不同的板块焊接而成的梁结构,是回转部分与车体大梁之间的过渡件,质量占比大,在保证底架刚度和强度的前提下,通过科学有效的方法对底架结构进行轻量化设计,对提升全炮的灵活机动性有着重要的意义[2]。对于单目标优化问题,当前已有诸多学者运用结构优化技术对火炮炮塔[3-4]、火箭炮基座[5]等关键部件进行轻量化设计,并取得了良好的减重效果。对于多目标优化问题,张鑫等[6]运用有限元仿真技术和响应面法相结合的优化技术,构建了响应面多项式函数近似模型,利用多目标遗传算法进行全局寻优,实现了火炮身管膛线的结构优化;朱孙科等[7]建立了复合材料定向管的多目标优化模型,并通过NSGA-Ⅱ遗传算法进行寻优,确定了复合材料的关键参数;萧辉等[8]提出了一种基于自适应径向基函数(RBF)神经网络的结构优化方法来解决火炮多学科多目标结构优化中计算冗长、收敛缓慢等问题,并通过实例证明了优化方法的可行性;葛尧等[9]采用了多岛遗传算法和非线性二次规划算法相组合对炮塔进行优化,并比较了不同算法的优化效率。
笔者先通过拓扑优化确定合理的底架结构材料布局,将基于RBF神经网络模型构建的代理模型引入到火箭炮底架多目标尺寸优化问题中,建立了较高精度的预测模型,大大降低计算时间;并在此基础上采用全局-梯度组合算法进行优化求解,即先采用多目标遗传算法进行全局寻优,通过得到的Pareto前沿解来指导二次寻优,再通过序列二次规划法在最优解附近进行二次梯度寻优,得到最优解。
1 底架结构与有限元建模
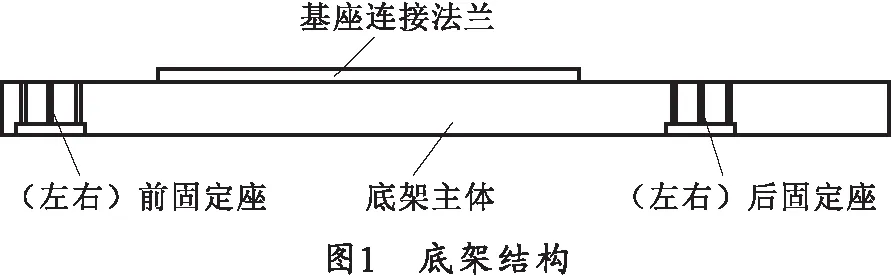
根据底架与下方车体及上方基座的连接关系,选取底架的最大外形轮廓建立如图1所示的初始几何模型。底架通过前后固定座与车体连接,基座连接法兰用于连接底架主体及基座。
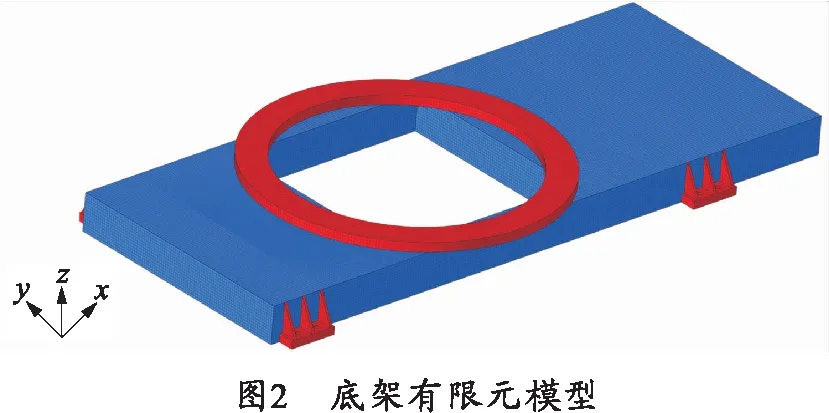
基于有限元前处理HyperMesh模块建立底架有限元模型,采用六面体实体单元进行网格划分。底架材料的弹性模量为210 GPa、泊松比为0.3,密度为7 850 kg/m3。底架有限元模型如图2所示。
分别选择火箭炮在发射及行军过程中的4种工况:0°方位射角、56°高低射角4发齐射;45°方位射角、45°高低射角4发齐射;x正方向过载1g加速度;z负方向过载1g加速度。将4种工况依次命名为S1、S2、S3、S4。
为使底架施加载荷更接近实际工况,底架上端支撑各部件用施加质量点代替,同时重力加速度方向沿着z轴负方向。在有限元模型中,固定座与车架之间的螺栓连接采用刚性(RBE2)单元模拟。S1和S2工况下,底架所受载荷以最大静载方式施加,将基座连接法兰上表面各节点作为受力点,采用柔性(RBE3)单元连接,其中主节点为基座连接法兰上表面所有网格节点,从节点为双储运发箱4发齐射时火箭发动机燃气流作用点。底架各工况下载荷施加情况如表1所示。

表1 底架各工况下载荷施加情况
2 底架结构拓扑优化
2.1 拓扑优化模型
拓扑优化的主要思路是通过传力路径,寻求设计空间内最优材料布局,从而得到性能最佳的结构形式。以体积为约束条件,柔度最小(即刚度最大化)为目标函数,建立数学优化模型,有:
(1)
式中:xi为优化设计变量;xmin为设计变量最小值;c为平均应变能;f为体积分数;v0为初始体积;u为位移矢量;N为单元总数;k和k0分别为优化前后的刚度矩阵。
采用变密度法,底架主体作为拓扑优化空间,每个单元的相对密度作为设计变量。以体积分数、基座连接法兰中心位移、柔度作为响应;以位移(不超过0.4 mm)和体积分数(不超过0.2)作为约束条件;以最小化柔度作为目标条件。在优化过程中,为防止出现棋盘格现象,设置最小成员尺寸(25 mm),同时考虑到优化模型的可制造加工性,设置左右对称模式的约束。
2.2 拓扑优化结果
采用OptisTruct求解器对优化模型进行计算,经33次迭代后收敛,取密度阈值为0.505,优化结果如图3所示。

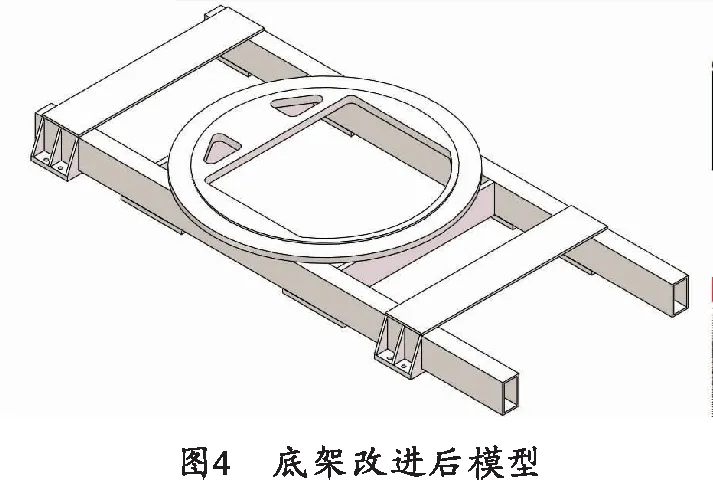
从图3可以看出,基座连接法兰左右两侧出现了较多的空心,材料布局形态接近梁结构,为便于生产制造可采用矩形梁作为底架主要承力部件,其余连接部位采用多薄板焊接结构。结合设计经验,底架改进后模型如图4所示。
3 多目标尺寸优化
3.1 有限元分析与设计变量选择
3.1.1 新底架刚强度分析
在有限元前处理软件Hypermesh中采用壳单元对新底架结构进行离散化,各部件采用焊缝(seam)单元进行模拟连接,边界条件与载荷的施加与拓扑优化部分相同。通过OptiStruct对上述有限元模型进行求解,结果如表2所示。

表2 新底架刚强度计算结果
计算结果表明,各工况下最大位移满足小于0.4 mm的设计要求且最大应力远小于材料屈服极限345 MPa,说明新底架结构在刚强度上留有较大余量,可进一步进行尺寸优化。
3.1.2 设计变量的选择
由表2看出,S1工况下对新底架刚强度要求较高;同时作为火箭炮支撑件的底架,其低阶振型对系统响应的贡献值大,即固有频率越低,越容易受到外界激励影响,因此同时在S1工况和自由模态两种工况下对新底架结构进行尺寸优化以使其结构性能达到最优。各优化部件如图5所示。
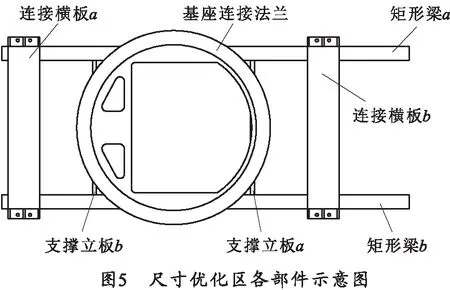
在优化过程中,将矩形梁、薄板、基座连接法兰等零件厚度作为设计变量,为保证得到较为合理的最优解集,选择各设计变量的最大范围来进行尺寸优化,如表3所示。
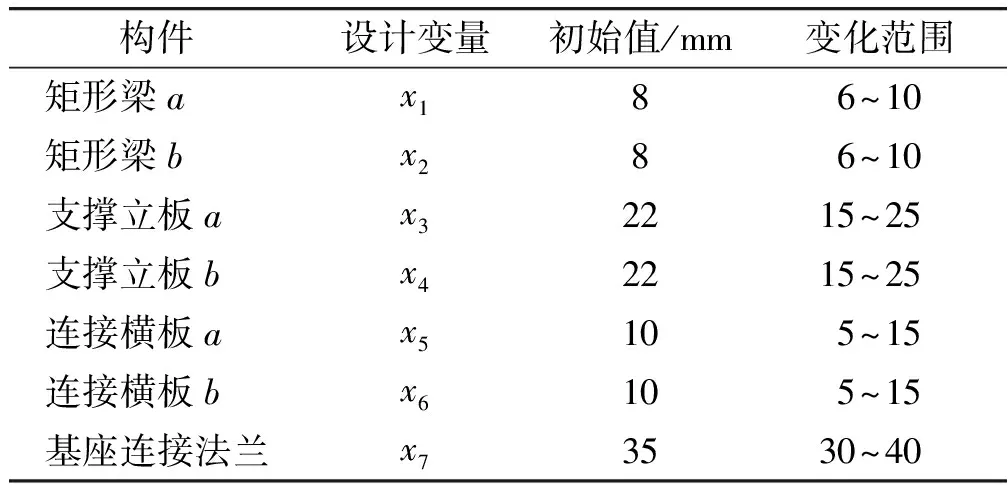
表3 各变量尺寸变化范围
3.2 RBF神经网络模型
3.2.1 哈默斯雷实验设计
优化过程中不断进行迭代,需要进行大量的有限元计算,用时较长,为更好地提升求解效率,通过实验设计获取合理采样点以准确地建立底架质量、比刚度结构效能和一阶模态频率的近似模型。在基于有限元法的设计实验中,常见的采样方法有拉丁超立方采样和哈默斯雷采样,二者均适用于响应面为高度非线性的情况。相比于拉丁超立方采样点仅在一维问题上有可靠的均匀性,哈默斯雷采样点能够在K维超立方体上有更可靠的均匀分布,基于哈默斯雷点,采用伪随机数值发生器,试图让落在每一个单位空间的点更平均。
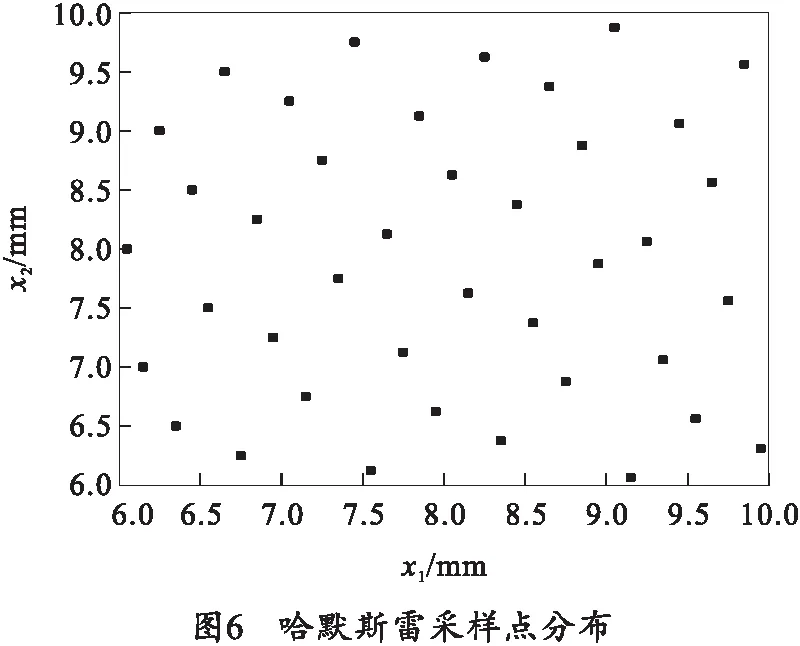
在优化软件中,以表3所列7个关键零部件厚度作为设计变量,以底架质量m、比刚度结构效能β、一阶模态频率f1为响应,采用哈默斯雷实验设计方法,其中因素为7个,得到40组样本数据,图6中仅列举了x1和x2采样点分布。
3.2.2 RBF神经网络模型的构建
径向基函数(RBF)神经网络模型是一种采用多元离散数据拟合未知函数的策略,具有较好的非线性逼近能力,可以更好地平衡求解效率和模型精度[10]。在联合仿真平台中采用了含有低阶多项式扩展项的RBF模型,输入层为7个设计变量,输出层为底架质量、比刚度结构效能和一阶模态。输出层与输入层之间的关系表达式为
(2)

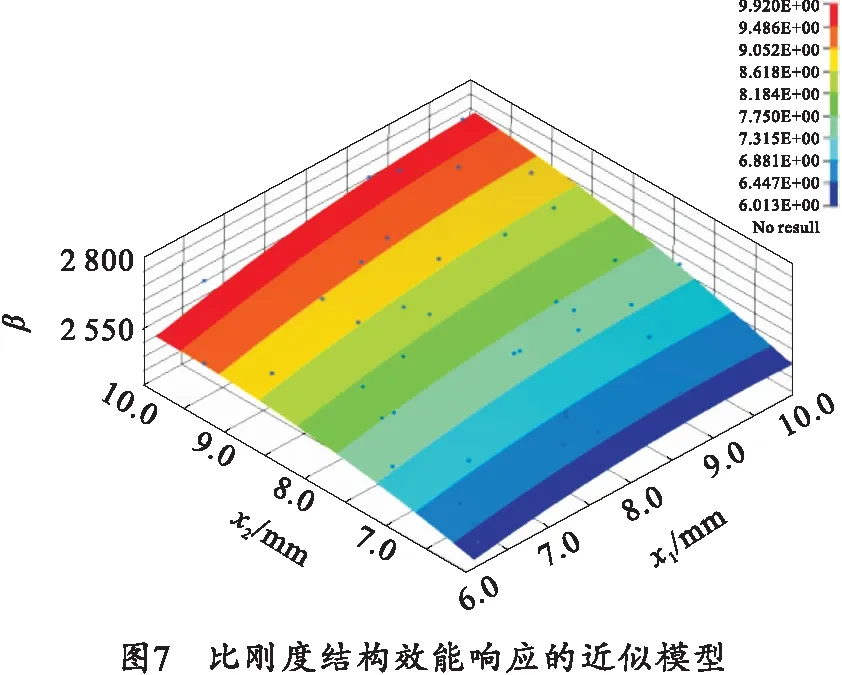
基于哈默斯雷实验设计得到40组样本数据点,通过RBF神经网络模型拟合底架质量、比刚度结构效能、一阶固有频率的近似模型,其中x1和x2的底架上比刚度结构效能β的RBF神经网络模型如图7所示。
近似模型的精度对优化结果的可靠性有很大影响,因此笔者采用决定系数R2来诊断拟合模型。
(3)
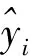
在设计空间中采用哈默斯雷实验设计方法随机抽取10个样本点对近似模型进行诊断,评价结果如表4所示。由表4可以看出,各响应的近似模型的决定系数R2均大于工程上要求的0.9且很接近1,说明采用RBF神经网络模型构建的近似模型满足精度要求,可进一步进行优化求解。

表4 RBF拟合模型精度评价
3.3 基于组合算法的优化设计
底架的优化问题中包含了7个设计变量,为解决在优化过程中寻求最优解困难的问题,采用了一种全局-梯度组合算法的优化策略来解决该类问题。先采用多目标遗传算法(MOGA)进行全局寻优,然后通过序列二次规划(SQP)在最优解附近进行二次梯度寻优,得到最优解。
3.3.1 基于多目标遗传算法的全局优化
底架的优化问题满足如下几方面条件:各设计变量在给定的上下限范围内取值;优化后底架在发射过程中产生的最大应力σmax小于材料的许用应力[σ],选择安全系数n=2,则许用应力[σ]=117.5 MPa;优化后的底架一阶频率f1大于86 Hz。优化目标为底架质量最小和比刚度结构效能最大,引用比刚度结构效能β来作为底架优化的目标函数[11]:
β=(E/s)/m,
(4)
式中:E为材料的弹性模量;s为结构变形;m为底架质量。比刚度结构效能值β越高,说明单位质量刚度越大。
基于上述分析,底架结构优化问题的数学模型表达式如下:
设计变量:X=[x1,x2,x3,x4,x5,x6,x7],
(5)
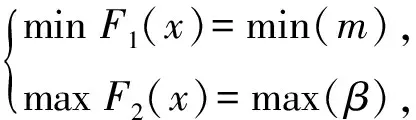
(6)

(7)
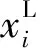
多目标遗传算法(MOGA)[12]全局搜索能力强,收敛速度快,可提供一系列的帕雷托解,并非是单一解,用来处理有约束或无约束的多目标优化问题,其计算流程如图8所示。

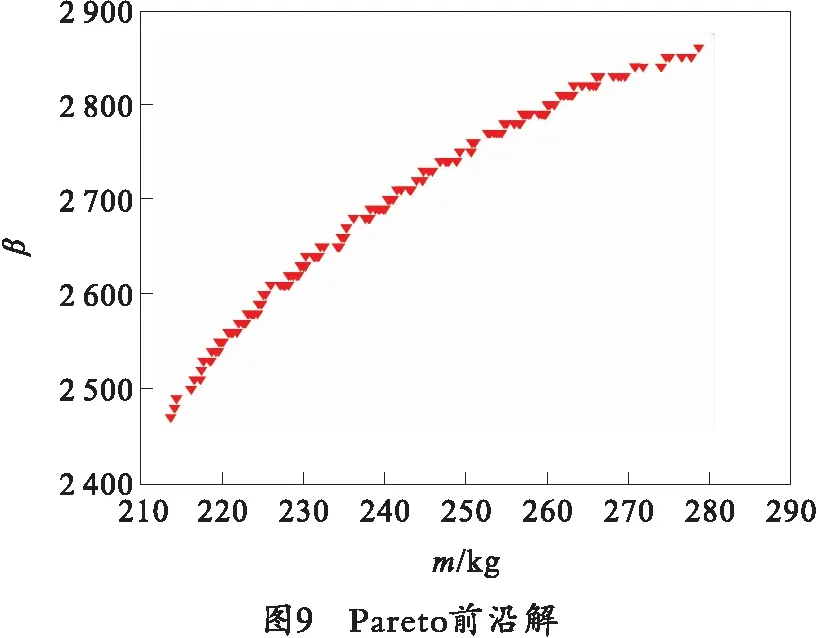
考虑到目标函数的收敛特性,将最大迭代次数调整为50,目标种群设置为114,通过迭代计算得到Pareto前沿解集如图9所示。由于MOGA并不存在全局最优解,而是不同子目标在不同的权重因子之下的一系列解集。不同子目标在理论情况下能够达到最优,但各目标不能同时达到最优,底架的质量减小必然导致比刚度结构效能的降低,无法令两个优化目标同时达到最优。为找到局部最优解,采用序列二次规划法在上述最优解附近进行二次梯度寻优。
3.3.2 基于序列二次规划法的梯度优化
为使优化后的底架结构刚强度得到改善,应保证优化后底架结构的比刚度结构效能大于初始值2 558,由图9看出,比刚度结构效能β达到2 600左右时,质量约为225 kg,减重效果明显。为序列二次规划法重新设置约束条件,设计变量不变,优化目标仅为底架质量最小,约束条件表达式为
(8)
序列二次规划法是求解带约束优化问题的典型方法,思路是在原模型上构建拉格朗日二阶近似模型并进行求解以判断下一步搜索方向,不断进行该步骤的迭代直到收敛至最优解:
x(k)=x(k-1)+aq,
(9)
式中:a代表寻优过程中确立的步长;q是求解二次规划子问题确定下一步搜索方向。确定q的过程中应使其满足约束条件并不断达到最优,搜索过程中的约束被线性化表述为
(10)
式中:C(k)代表目标函数f在点x(k)的Hessian矩阵正定的一阶近似;gi为约束条件。
二次梯度寻优迭代曲线如图10所示,可看出局部搜索速度加快,在多目标遗传算法求解的基础上,得到了局部最优解。优化后质量为230 kg,较优化前的280.1 kg降低了50.1 kg,优化后各参数如表5所示。

表5 底架优化前后性能参数

4 优化结果及分析
该防空火箭炮为双储运发箱发射结构,底架为左右对称结构,考虑到生产制造,对优化值进行圆整,并在有限元模型中对圆整后的结果进行校验,底架优化前后性能参数如表5所示。优化后的底架结构一阶模态得到改善;虽然最大应力和最大形变有所增加,但都在设计范围之内且分布情况与优化前相比无明显变化;底架比刚度结构效能得到提升,说明单位质量的刚度裕度得到改善;优化后底架质量为238.3 kg,较优化前底架质量280.1 kg减少了42.7 kg,减少了15.2%,减重效果明显。
5 结论
1)基于多工况拓扑优化寻找出底架在设计空间中的最佳材料布局。
2)采用哈默斯雷实验设计方法减少了实验次数,基于RBF神经网络模型构建了高精度的底架质量、比刚度结构效能、一阶模态近似模型,实现了底架关键零部件尺寸与结构性能的关系从隐式到显式的可视化。
3)基于近似模型,采用多目标遗传算法和序列二次规划法的组合优化策略,先通过多目标遗传算法进行全局寻优,再采用序列二次规划法进行二次梯度寻优,逐步逼近寻得全局最优解。
4)最终优化结果表明,优化后底架结构的一阶模态和比刚度结构效能得到改善,底架质量减小15.2%,达到轻量化目标,优化方法可供类似结构参考。

