电热化学炮同轴浮动电极式表面放电等离子体的数值模拟
陈一波,栗保明
(南京理工大学 瞬态物理国家重点实验室,江苏 南京 210094)
等离子体发生器用途广泛,在工业上常用于切割、焊接等,在科学研究上可用于物理学实验[1]。用于电热化学炮的等离子体发生器按其等离子体电弧所处位置可分为轴线式和同轴式等离子体发生器。轴线式等离子体发生器的等离子体电弧位于放电室的中心轴线上,等离子体电弧引爆后向放电室外喷射以点燃发射药。同轴式等离子体发生器的等离子体电弧环绕位于中心轴线处的消融材料棒,与发射药距离更近、接触面更大。同轴浮动电极式表面放电等离子体发生器属于同轴式等离子体发生器,其拥有数个浮动电极,各电极沿柱状聚乙烯壁周期性排列,通过施加数十千安以上的强电流使电极间沿聚乙烯表面生成等离子体电弧并向四周喷射,工作区域大,等离子体电弧与炮膛内发射药直接接触,点火性能好,是一种应用于电热化学炮的新式等离子体发生器[2]。然而前人对此种等离子体发生器物理场的研究较少,且仅有的相关研究并未考虑到等离子体的产生、流动与吸收,也未讨论浮动电极所受的洛伦兹力。笔者对等离子体电弧物理场重新建立了准瞬态数学模型,使用计算流体动力学(CFD)有限元分析软件ANSYS FLUENT[3],编写用户自定义方程(UDF)添加了烧蚀方程和磁流体动力学(MHD)模型,并采用较为适合计算等离子体电弧湍流的剪切应力湍流模型(SST)进行仿真[4-5]。同时选取了几种不同电极尺寸与排列间距分别计算等离子体电弧物理场,并进行了后处理,对电阻、温度、洛伦兹力、烧蚀质量流率进行了分析。
1 数学模型
1.1 基本假设
等离子体电弧是不可压缩的连续流体;等离子体电弧处于湍流状态;等离子体电弧满足局部热力学平衡条件;等离子体电弧传热符合Rosseland辐射传热模型[6];忽略旋流分量和重力。
1.2 计算区域
图1是同轴浮动电极式表面放电等离子体发生器剖面图,其中心部位为被聚乙烯壁包裹的输电杆,阳极在其上端,电流自阳极向下流过;固体为等间距排列在输电杆聚乙烯壁上的浮动电极,与输电杆相绝缘;在等离子体区域电流向上流经浮动电极流回阴极。由于浮动电极的周期性排列,可将同轴浮动电极式表面放电等离子体发生器视为大量等效的等离子体发生单位的串联[7-8],笔者选取其中一个等离子体发生单位进行计算,并忽略边缘效应。

如图2所示,其中ABCDEFGH围成的区域为等离子体电弧计算区域,CH为旋转对称轴,AB为等离子体流出边界,AH与BC的延伸仍为等离子体电弧,CD与GH为聚乙烯壁。计算区域长xm,宽ym,浮动电极长xs,宽ys。
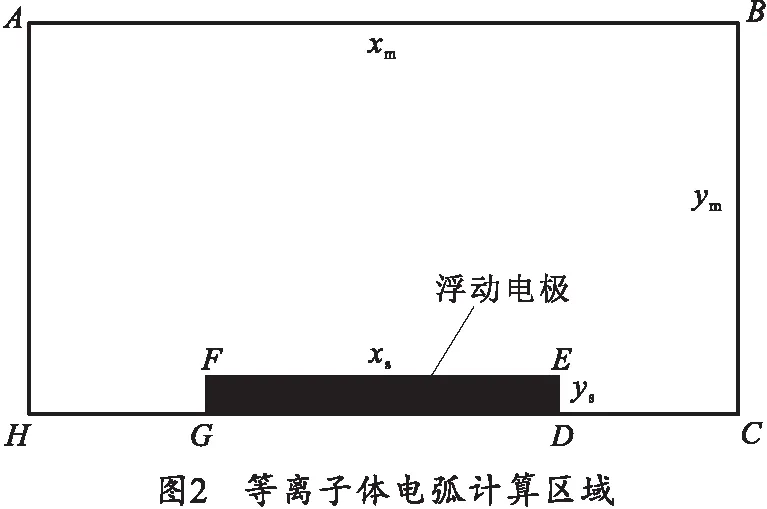
1.3 控制方程
FLUENT软件中内置了流体基本的质量连续性方程、动量守恒方程、能量守恒方程[9],以及数种湍流模型。采用充分考虑了低雷诺数和剪切流的剪切应力模型(SST)作为湍流模型。
需要编写UDF添加的烧蚀方程为
(1)
式中:Γ为烧蚀率;f为比例常数;σsb为黑体辐射系数;T为温度;ha为烧蚀焓。
式(1)确定了聚乙烯壁的烧蚀质量通量,由灰体辐射模型法计算所得[10-11]。
需要编写UDF添加的磁流体动力学模型包括:
1)电流连续性方程为
(2)
式中:r为径向坐标;x为轴向坐标;jx和jr分别为轴向和径向电流密度。
2)根据欧姆定律得到
(3)
(4)
式中:σ为电导率;φ为电势。
3)磁矢势方程:
(5)
(6)
式中:μ0为真空磁导率;Ax和Ar分别为轴向和径向磁矢势。
4)磁感应强度切向分量:
(7)
式中,Bθ为切向磁感应强度。
与等离子体运输相关的动量与能量守恒通过编写UDF程序加入FLUENT的动量与能量方程源项来实现:
1)向FLUENT添加轴向动量方程源项Fx:
Fx=jrBθ.
(8)
2)向FLUENT添加径向动量方程源项Fr:
Fr=-jxBθ.
(9)
3)向FLUENT添加能量方程源项Sh:
(10)
式中:kB为玻尔兹曼常数;e为基本电荷;σR为斯特藩-玻尔兹曼常数;λR为分子平均自由程。
式(8)、(9)为洛伦兹力,式(10)第1项为焦耳热,第2项为洛伦兹功,第3项为Rosseland辐射传热模型。
式(2)~(10)实现了在FLUENT中建立完整的磁流体动力学(MHD)模型。
1.4 边界条件
1)质量边界条件:CD与HG为质量入口边界,质量通量设置为式(1)。AB为压强流出边界,压强为101.325 kPa(1个大气压)。
2)MHD模型边界条件:BC和AH可设定电势值或总电流密度。浮动电极的电导率取黄铜电导率1.57×107S·m-1。等离子体工作气体为聚乙烯等离子体,采用的等离子体输运系数见文献[12]。另外,在CH处通入从H流入、从C流出的同值反向电流,并与其余各部分绝缘。
3)能量方程边界条件:浮动电极温度为300 K,AH与BC为绝热光滑表面。
2 求解过程
同轴浮动电极式表面放电等离子体发生器工作时间短,仅为数毫秒,每平方厘米聚乙烯壁被烧蚀损失的质量不到十毫克,因此尺寸上的变化可以忽略不计,网格种类选用固定网格。利用FULENT前处理软件GAMBIT将计算域按正方形网格划分,总网格数为16 800,节点数为17 131。
将编写好的UDF编译后导入FLUENT软件,并添加3个用户自定义标量:UDS-0、UDS-1、UDS-2,分别用于计算电势φ和两个磁矢势Ax、Ar,同时将边界条件各参数输入FLUENT软件中,选定耦合(Coupled)与准瞬态(Pseudo Transient)解算方法。
由于聚乙烯等离子体的物理特性随温度变化,电场、磁场、流场、温度场等各物理场之间相互耦合,需使用物理环境间接耦合法进行处理。在每一轮迭代中,首先根据初值计算出电场环境中的电势分布;然后由欧姆定律得到电流密度分布,并将电流密度的计算结果输入磁场,得出磁感应强度;之后将电磁力、焦耳热、洛伦兹功、辐射传热等作为体积力、体积生热代入流场中,求解速度和温度的分布;最后将上述计算所得到的速度和温度分布作为新的初值代入电场中开始新一轮的计算,反复迭代,直到计算收敛。由于UDF方程和源项的添加导致迭代计算过程容易发生振荡,甚至是发散。为使求解顺利进行,根据前人的研究[13],笔者在设计中提高了网格的质量,最小正交质量(Minimum Orthogonal Quality)为1.00;并设置较小的温度亚松弛因子为0.6。
3 计算结果分析
3.1 等离子体发生器物理场的计算结果和后处理
本例中所采用的等离子体发生器为12个发生器单元串联而成,每个单元尺寸为:xm=18 mm,xs=12 mm,ym=10 mm,ys=1 mm。取总电流为70 kA时仿真所得的各物理场为例进行分析。
图3为计算所得的等离子体电弧电势分布,可见由于浮动电极的电导率远大于等离子体电弧,所以浮动电极自身的电势差非常小,而在浮动电极以外的等离子体中电流密度正比于电势梯度,因此在E点和F点的电流密度是最大的。

图4为等离子体电弧的磁感应强度分布,越靠近计算域对称轴则磁感应强度越大,在AB边界的磁感应强度接近0 T。
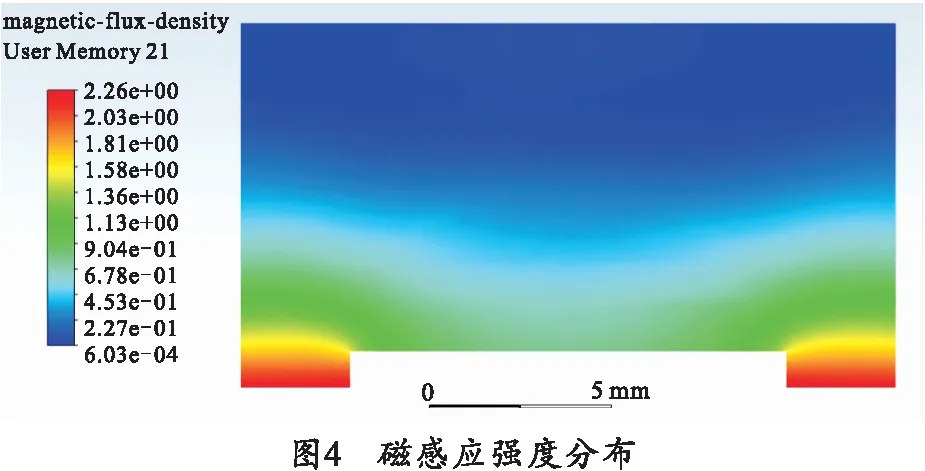
图5为等离子体电弧的速度矢量,可见电流密度与磁感应强度较高的地方所受洛伦兹力也较大,速度更高。

图6为等离子体电弧温度分布,位于聚乙烯壁正上方、距离各个热量流出边界较远的位置电弧温度最高,为28 100 K,并比周围的温度分布更加集中。
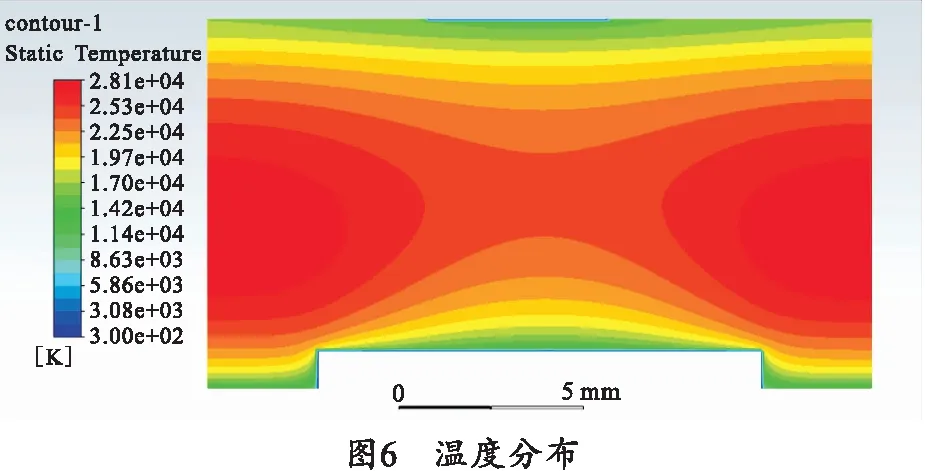
温度分布是所有物理量共同作用下的结果,也是模型每一步迭代求解的最后一部分,因此通过对比温度分布能够说明模型的正确性。本模型所得到的温度分布方式与文献[14]给出的几乎完全一致,如图7。
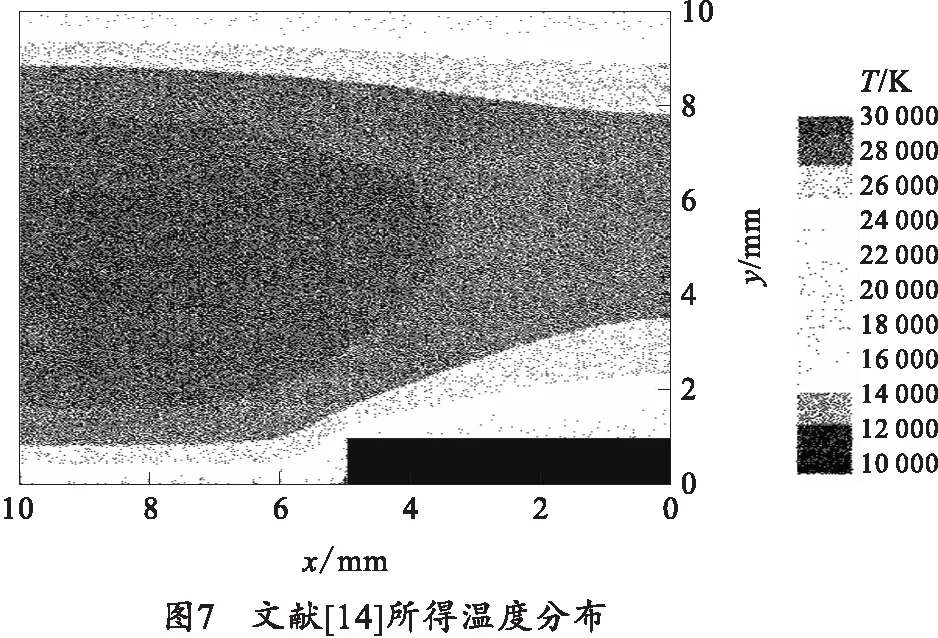
利用FLUENT的后处理功能对所得物理场进行分析,得到此时发生器总电势差为84 V×12=1 008 V;电流为70 kA,发生器单元电阻为84 V/70 kA=1.2 mΩ;发生器总电阻为1.2 mΩ×12=14.4 mΩ。
利用后处理功能在DE、EF、FG边界上对垂直于表面的电流密度进行积分,可以得到流经浮动电极的总电流为32.9 kA,同时可以算出作用于浮动电极的洛伦兹力为789.6 N,方向向外。在理想状态下,由于电流的轴对称分布,浮动电极所受的洛伦兹力仅为内力,合力为0,然而实际上在起弧的瞬间电流分布可能并不均匀,因此整个等离子体发生器可能会遭受到由洛伦兹力产生的力矩。这里所给出的洛伦兹力可作为计算这种力矩上限的参考以及作为等离子体发生器力学特性分析的依据[15]。
利用后处理功能对烧蚀边界CD和GH的烧蚀率进行积分可求得此时CD和GH的烧蚀质量流率之和为6.550 g/s,12个发生器单元的总烧蚀质量流率为78.60 g/s。
3.2 各电流值仿真结果与实验对比
仍然采用3.1节中实例的尺寸,选取了数个不同电流值进行仿真,并选取自由放电实验中相同电流值下所测得发生器总电阻值相比较,如表1所示。可见,仿真结果与实验符合较好,相对误差绝对值在5%之内。
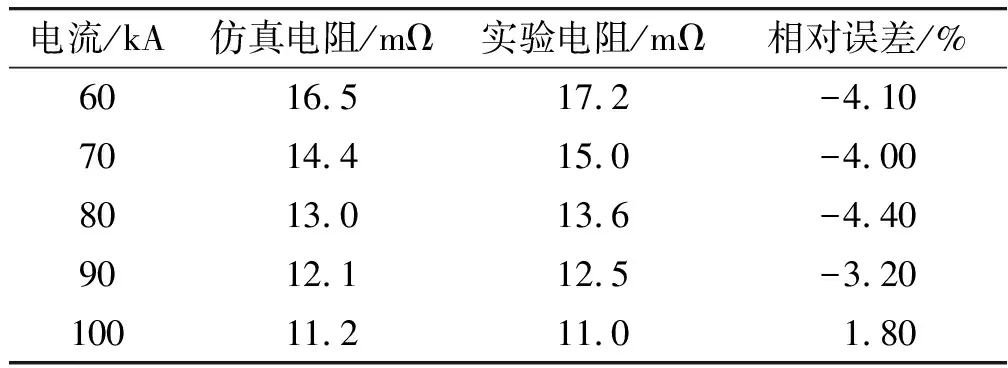
表1 仿真结果与实验电阻值对比
3.3 电极尺寸与排列间距对物理场的影响
以3.1节中实例尺寸为基础,当总电流均为70 kA时,对调整了电极尺寸与电极排列间距的等离子体发生器物理场进行仿真;并将得到的结果在表2中进行对比。
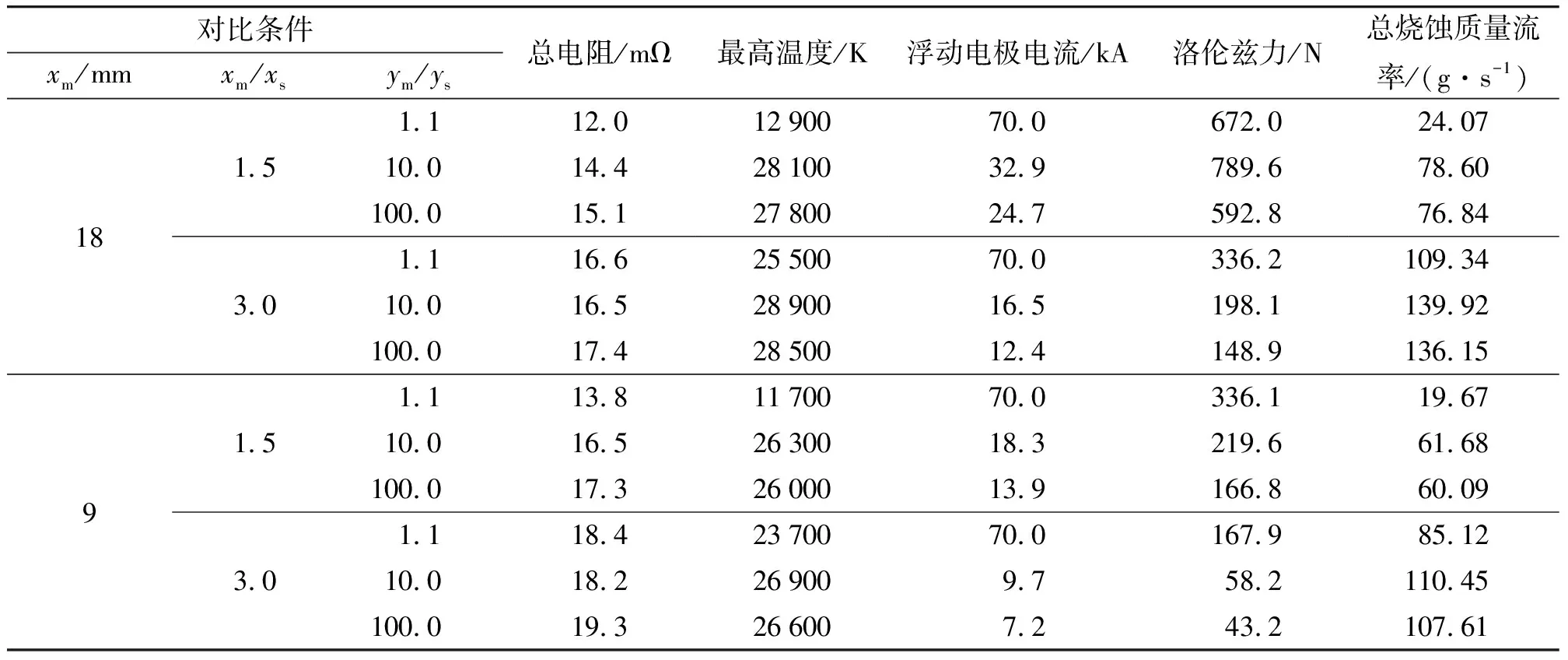
表2 不同条件下物理场仿真结果对比
在尝试的各种情况下,通过浮动电极的电流都与浮动电极的厚度和宽度正相关,而浮动电极通过的电流越大、浮动电极自身的宽度越大,其所受到的洛伦兹力也就越大。从建立的烧蚀模型可知,总烧蚀质量流率与烧蚀边界温度正相关,正比于烧蚀边界的总长度,因此最高温度较高时总烧蚀质量流率也较高,最高温度和烧蚀边界长度均较高时总烧蚀质量流率最高。总烧蚀质量流率直接决定了等离子体电弧向质量流出边界扩散的速度,也决定了通电时刻与等离子体电弧点燃质量流出边界外发射药的时刻的时间间隔[16]。
在xm/xs=1.5时,总电阻随着浮动电极的厚度减小而增加;最高温度主要取决于等离子体电弧的热量流出,其次取决于等离子体电弧的电阻率即产热能力。而在xm/xs=3.0时,由于浮动电极宽度的缩小、等离子体电弧的空间增大,等离子体电弧的热量流出相对较小,热量也更容易聚集在两浮动电极之间,此时电阻率对最高温度的影响相对变大。
通过表2的对比,发现等离子体发生器单元间距变小则电阻率变大,原因是间距的变小使得热量流出边界相对变大,热量也更难聚集在两个浮动电极之间,而过大的等离子体发生器单元间距则可能会使整体温度分布不均匀。另外,等离子体发生器单元间距变小后流过浮动电极的电流变小,因此洛伦兹力也减小。
在所尝试的情况下,xm=18 mm、xm/xs=3.0、ym/ys=10.0应当是最理想的等离子体发生器尺寸,因为此时等离子体发生器总电阻较大,温度最高,可见对电流的利用效率较高;浮动电极受到的洛伦兹力较小,对结构强度的要求相对降低;总烧蚀质量流率最大,点火性能最好。
4 结论
1)给出了计算电热炮同轴浮动电极式表面放电等离子体发生器物理场的完整磁流体动力学准瞬态数学模型,通过UDF技术对ANSYS FLUENT二次开发实现了该种等离子体发生器物理场的仿真,仿真结果与相关文献实验所得符合较好。
2)对该种等离子体发生器物理场仿真的后处理结果显示了每个浮动电极可能遭受的洛伦兹力,以及整个等离子体发生器因此受到的最大力矩,可用于该种等离子体发生器力学特性分析。
3)用上述方法对调整尺寸后的同轴浮动电极式表面放电等离子体发生器进行仿真和对比,定性地得到了该种等离子体发生器物理场与其不同尺寸、不同间距的规律,选定了一种较优尺寸,该尺寸及本文仿真分析方法均可供同类等离子体发生器设计参考。

