5G NR RSRP测量算法研究
邓炳光 张旭辉 李金艳 张 蕾 梅承力
1(重庆邮电大学通信与信息工程学院 重庆 400065) 2(中国电信股份有限公司技术创新中心 北京 102209)
0 引 言
RSRP是代表无线信号强度的关键参数,用于衡量系统接收信号强度。本文分析多种RSRP的评估方法,包括现有的基于均值的方法和基于共轭相乘的方法。现有多数测量方法多采用均值的方法或者通过对均值法的进一步改进以降低测量的鲁棒性[1]。但是在低信噪比的情况下噪声的影响会带来无法消除的误差,或是需要通过大量且多次的计算测量才可以达到较高的测量准确性[2]。本文提出一种基于子集共轭相乘的新算法,并与当前主流算法进行对比,得到算法的适应情况和对其他算法的优劣。
1 RSRP测量流程
RSRP测量的过程与小区搜索密切相关,所以RSRP的测量流程是从小区搜索之后开始的[3]。当小区搜索成功后,对数据进行遍历补偿和去直流,再通过FFT进行补偿,然后计算RSRP和RSRQ值[4]。测量流程如图1所示。
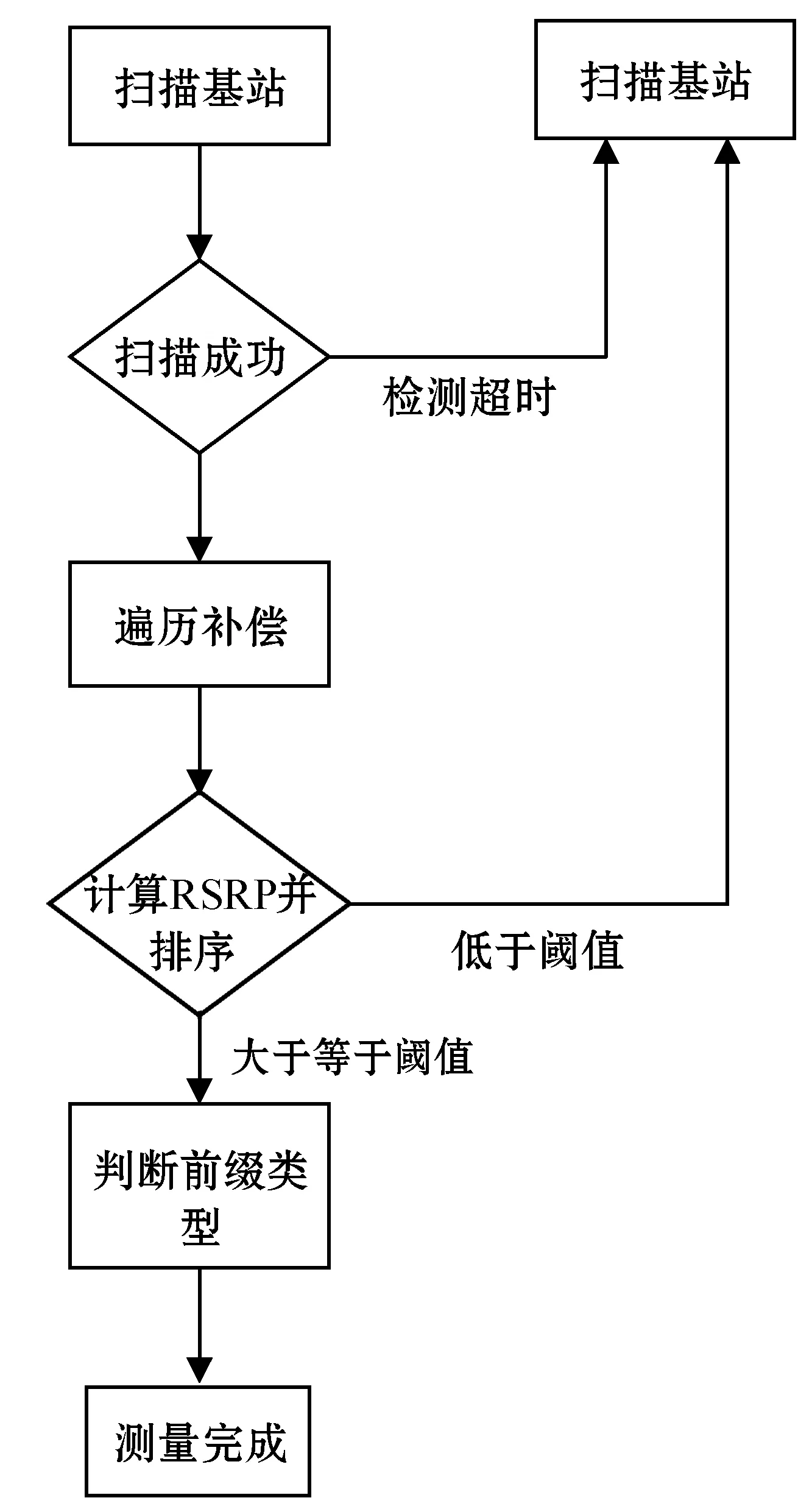
图1 RSRP测量流程
假设接收到的传输信号为R(k,l),则接收到的参考信号能量可以用式(1)来表示。
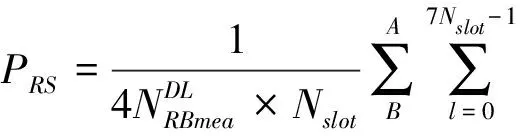
(1)
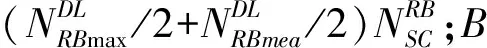
如果直接通过接收到的信号来计算RSRP,里面必然包含了部分噪声的能量,而RSRP是不反映该小区噪声能量的,因此PRS不能直接反映信号能量RSRP,RSRP必须用式(2)表示。
RSRP=PRS-Pnoise
(2)
式中:Pnoise是测量带宽内每一个资源子块上的噪声平均值。在没有传输信号的保护带宽内,Pnoise可以通过保护带宽内接收到的信号来计算获得,但是传送了信号的资源子块上,Pnoise很难计算。所以这里需要其他的办法来减少噪声对RSRP测量的影响[5]。
其中Pnoise是测量带宽内每一个资源子块上的噪声平均值。在没有传输信号的保护带宽内,Pnoise可以通过保护带宽内接收到的信号来计算获得,但是传送了信号的资源子块上,Pnoise很难计算。所以这里需要其他办法来减少噪声对RSRP测量的影响[5]。
2 CSI-RS
CSI-RS采用伪随机序列,通用伪随机序列由长度为31的Gold序列定义,由两个m序列产生[6],根据协议3GPP TS 38.211,CSI-RS序列r(n)具体生成公式如式(3)所示。
(3)
初始化为式(4)。
(4)
式中:在每个OFDM 符号的起始处nS是无线帧内的插槽号;l是一个槽内的 OFDM符号;nID与高层参数scramblingID相关[7]。
从参考信号时频资源系列上接收数据序列Z1(k),其中k为1~K1,K1为数据序列Z1(k)的长度,Zi(k)表达式为:
Z1(k)=H11(k)×X1(k)+X12(k)×X1(k)+N1(k)Z2(k)=H21(k)×X2(k)-X22(k)×X2(k)+N2(k)
(5)
式中:H(k)表示信道响应系数;X(k)表示参考信号时频资源上的信息序列N(k)表示干扰和噪声[8]。参考信号时频资源系列上接收数据序列Zi(k)除以参考信号序列Xi(k)得到z(k):
z1(k)=Z1(k)/X1(k)=H11(k)+H12(k)+N1(k)/X1(k)z2(k)=Z2(k)/X2(k)=H21(k)-H22(k)+N2(k)/X2(k)
(6)
将上面两个式子相加(相减)除以2后得到新的z1(k)(z2(k)):
z1(k)=(z1(k)+z2(k))/2=H11(k)+N1(k)/2X1(k)+N2(k)/2X2(k)z2(k)=(z1(k)-z2(k))/2=H21(k)+N1(k)/2X1(k)-N2(k)/2X2(k)
(7)
3 均值算法
由于噪声对终端进行一系列性能测量评估有着较大的影响,尤其是在低信噪比情况下,误差会更加严重以至于得到的测量结果无法使用[9]。当前业界最普遍使用的测量评估方法是基于均值的测量算法,基于均值的测量算法不仅在仿真计算时的计算量小,而且在实现方面也经过许多验证,更加方便且成熟。
基于均值的测量算法本质是将接收到的参考信号累加起来并求均值,以此来减小噪声对测量结果的影响。因为信道中噪声多为高斯白噪声,而且高斯白噪声服从均值为零的独立不相关高斯分布,那么得到信道估计值Zi后可以将信道估计值求均值以降低高斯白噪声的影响,使得测量结果更加接近理论值[10]。使用基于均值的评估方法进行RSRP估计后得到的估计值为:
(8)
式中:Hi表示参考信号位置上的信道频率响应;Xi表示第i个参考信号位置上的参考信号;Ni表示高斯白噪声,高斯白噪声是独立分布且均值为零的;PN是高斯随机变量的方差;E为信号能量系数;I为参考信号总量。
图2是基于均值的测量算法估计的RSRP仿真结果。可以看出在低信噪比的情况下基于均值的测量算法所估计的值比高信噪比下的RSRP值更大。在LTE系统中普遍使用基于均值的测量算法是因为算法复杂度低、算法实现成熟且易于验证,还有一个重要的原因就是因为LTE使用的测量带宽较小(如1.4 MHz)。在相同的信道情况下,因为较小的测量带宽(1.4 MHz)多个信道值所占的时间比较大的测量带宽(20 MHz)小,所以相对于较大的测量带宽信道的变化程度更小,因此信道的影响也比较大的测量带宽小。但是5G NR系统中测量带宽的变大使得多个信道估计值经历的时间延长,变化幅度增大,因此对于噪声而言,更多的影响因素变成信道误差造成的结果。如果还使用基于均值的测量算法,那么测量带宽就不能过大,这与5G的带宽要求不匹配。

图2 均值的测量算法估计RSRP
4 共轭相乘算法
由于基于均值的测量算法在低信噪比的情况下需要更窄的测量带宽,而在5G系统下测量带宽较大,测量估计值在低信噪比的情况下会有较为严重的误差,不能在现实环境中使用,因此提出基于共轭相乘法来进行RSRP值的估计测量。
基于共轭相乘测量算法相邻参考信号的子载波上信号分量的相关值为PH,而噪声分量是独立的,相关值为零。基于共轭相乘的测量算法将一个OFDM符号上参考信号的所有资源粒子(RE)的接收信号z(k)与相邻接收信号共轭相乘后取实部得到信号的直流分量,再求均值计算得到估计的RSRP值。进行共轭相乘并累加:
(9)
计算测量带宽内z(k)共轭相乘并累加后的均值并转化为对数形式:
(10)
RSRP=10log10(RSRP)
(11)
图3是基于共轭相乘的测量算法估计的RSRP仿真结果。可以看出在不同信噪比的情况下基于共轭相乘的测量算法估计的RSRP值变化不大,因为噪声分量是相互独立的,共轭相乘后会消除一部分的噪声分量,所以经过共轭相乘后噪声消除一部分均值后噪声又会消除一部分,噪声对RSRP值的影响已经降到非常低的程度。
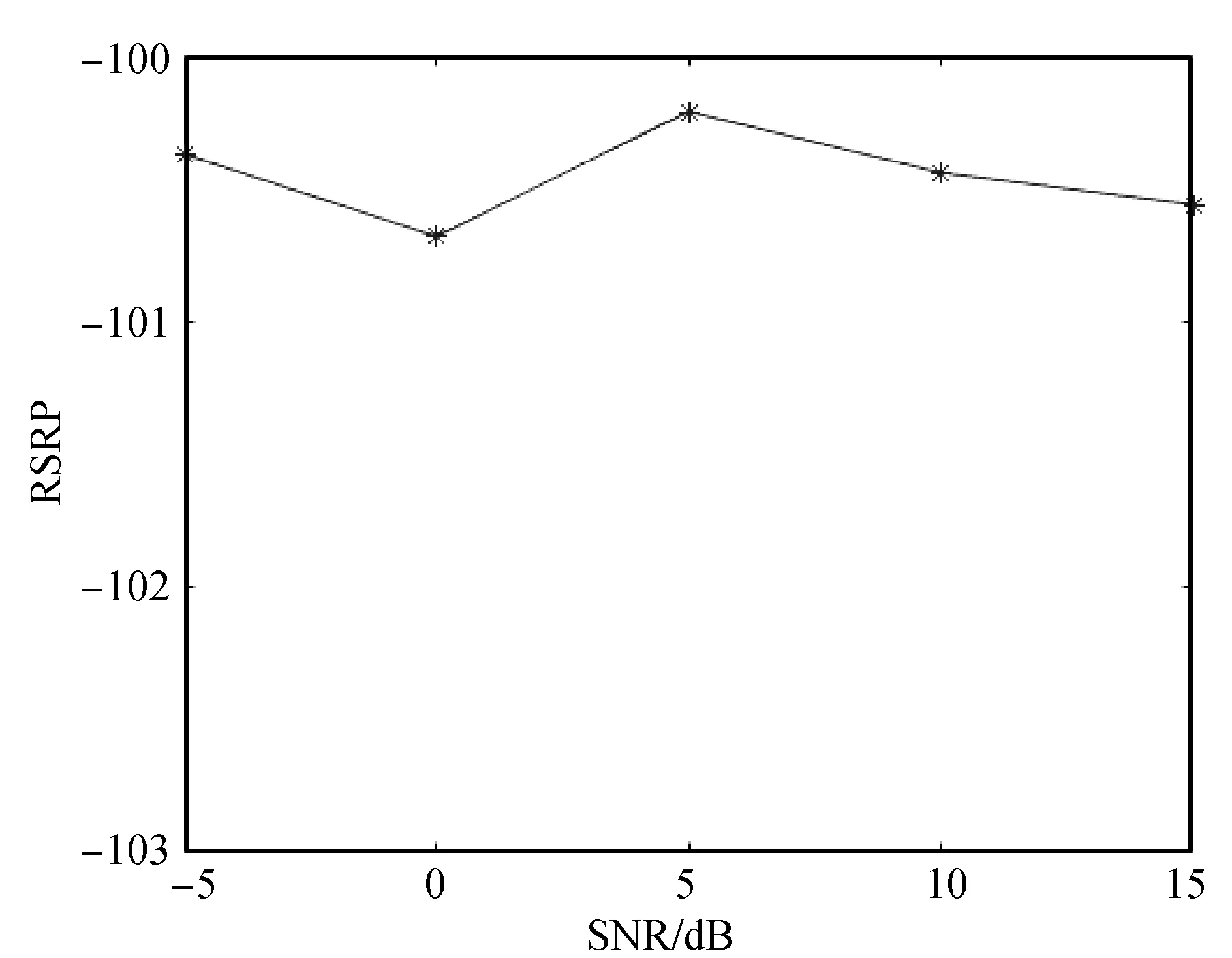
图3 共轭相乘的测量算法估计RSRP
但是信噪比的大小还是会影响到RSRP的测量,并且在带宽变化和信噪比变化的共同影响下,基于共轭相乘的测量算法得到的RSRP估计值还是会略小于理论值。信噪比越高,估计的RSRP测量估计值就越大;测量带宽越大,估计的RSRP测量估计值就越大。
5 子集共轭相乘算法
在共轭相乘测量算法的基础上,提出基于子集共轭相乘测量算法。在共轭相乘测量算法的基础上可以把I个承载参考信号的RE划分成M个N大小的子集集合。均值法的思想是假设所有RE经历的信道和估计值是相似的,所以可以使用求和再求平均的方法来降低噪声的影响,但是5G NR系统中测量带宽的变大使得多个信道估计值经历的时间变长,变化幅度变大,所以全部求均值就不太合理。而划分成大小相同的子集,再在各自子集中求均值就可以避免不同子集差距过大但是还要求平均的情况。进一步地,将各个子集和相邻子集求共轭相乘值可以避免信道区别过大而进行均值计算的粗暴算法。
将I个承载参考信号的RE划分成M个N大小的子集集合,再利用均值来进一步降低结果鲁棒性,得到RSRP值:
(12)
式中:ZNm+n为M中的第Nm+n个子集。
这是划分成M个N大小的子集集合后再进行均值,得到M个N大小的子集集合后不进行均值计算,而是进行相邻子集的共轭相乘计算,先得到M个N大小的子集集合:

(13)
如果不划分为M个N大小的子集集合而只是单纯地计算共轭相乘值,那么在5G系统中测量带宽的变大使得多个信道估计值经历的时间变长,变化幅度变大的情况下相邻参考信号的信道估计值会经历大的变化而使得不能进行共轭或者均值计算。因此我们把I个承载参考信号的RE划分成M个N大小的子集集合,进一步降低相邻单个信道估计值计算的影响。将相邻子集进行共轭相乘,得到RSRP值:
(14)
图4是基于子集共轭相乘的测量算法估计的RSRP仿真结果。可以看出在不同子集大小情况下RSRP估计值的变化,在低信噪比的情况下子集数相对较多的估计值所受影响更小;随着信噪比的变大,子集数相对较少的估计值反而所受影响更小。当子集数等于1时,子集共轭相乘测量算法就变成了共轭相乘法,从图中可以看出,在子集数等于1时的RSRP值还是要小于部分子集数不为1时的RSRP估计值,因为在5G系统下信道的变化情况多且大,所以单纯的共轭相乘依然会因为相邻参考信号变化差距过大而造成一定影响。

图4 子集共轭相乘的测量算法估计RSRP
在相同的信道情况下,可以通过增加不同的子集个数来进行子集间的共轭相乘,可以降低噪声对测量估计值的影响,但是当子集个数过多时,又无法保证相邻子集内信道估计的相似性,会造成与单纯使用共轭相乘法一样的影响,即信道对测量结果的影响占主要部分。因此可以在不同的信噪比情况下使用不同的子集个数。
基于子集共轭相乘法复杂度较高,而且在5G系统信道复杂的情况下,实际的信道参数和信噪比精度确定比较困难,在确定不同信噪比情况下的子集个数时可能需要太多次尝试,对最优子集的选择比较困难。因此基于子集共轭相乘法的测量算法也是一种在理想情况下的模拟算法。
6 结 语
本文就当前使用最多的基于均值的测量算法与理论改进较多的共轭相乘法进行比较,得到两种方法的优势和各自的不足之处。均值法计算复杂度最低,最易于实现和验证,但是更适合使用在测量带宽较小、信噪比高和信道变化不大的情况下,但是5G系统下测量带宽较大而且信道变化大,因此均值法并不是最适合5G系统的测量估计算法。共轭相乘法是当前理论中替代均值法最多的算法,基于共轭相乘的测量算法更适合在带宽较大的情况下,并且带宽越大,RSRP测量估计值越大,但是共轭相乘法需要相邻信道估计值变化不大,这又是一个对5G系统下测量的约束。本文提出基于子集共轭相乘的测量算法,算法将I个承载参考信号的RE划分成M个N大小的子集集合,再把子集进行共轭相乘,避免了只进行共轭相乘带来的信道影响的累积,但是需要在不同的信噪比情况下选择不同的子集数,由于5G系统下对信道参数的确定比较困难,所以基于子集共轭相乘的测量算法暂时也只是一个理论上的算法。
均值法、共轭相乘法和子集共轭相乘法在不同的情况下各自有不同的特点,在5G系统下共轭相乘法和子集共轭相乘法更具有优势。子集共轭相乘法在参数确定且精准的情况下,可以通过不同的子集数来进一步提高RSRP值,但是条件较为严苛。
因为子集共轭相乘法是一种新算法,希望在以后的5G系统发展中可以对算法进行进一步的改进,使之更适合今后的系统测量。

