顺“思”而为 借“思”而上
——三个数学案例的实录、评析和思考*
章祥俊 (江苏省苏州吴县中学 215129)
近年来,数学课堂的变化是巨大的,课堂教学过程中的问题驱动、活动引领、任务驱动、项目学习、单元设计等已经成为趋势.课堂教学中,以学生为中心,关注学生动手实践、自主探究、合作交流、问题解决等已经成为常态.[1]课堂教学中,我们应更多地关注学生的自主空间,关注学生的主动学习,关注学生的主体意识,实现学生的自我价值,激发学生的学习动力,顺势而为,借思而上,引导学生深度思考,促进学生学会学习.本文拟结合三个案例具体谈一谈.
1 顺“思”而为,引发自主探究,促进学生主动学习
案例1求函数f(x)=x2-2x-3,x∈R的最小值.
生:因为f(x)=x2-2x-3=(x-1)2-4,所以函数f(x)的最小值为f(1)=-4.
设计问题 以二次函数为背景,请你命制一道求函数最值的题目.
生1:求函数f(x)=x2-2x-3,x∈[2,3]的最小值.
生2:求函数f(x)=x2-2x-3,x∈(2,3)的最小值.
生3:求函数f(x)=x2-2x-a,x∈[2,3],a∈R的最小值.
生4:求函数f(x)=x2-ax-3,x∈[2,3],a∈R的最小值.
生5:求函数f(x)=ax2-2x-3,x∈[2,3],a∈R的最小值.
生6:求函数f(x)=x2-2x-3,x∈[a-1,a+1],a∈R的最小值.
生7:求函数f(x)=ax2-2ax-3,x∈[2,3],a∈R的最小值.
生8:求函数f(x)=ax2-bx+c,x∈[m,n],a,b,c,m,n∈R的最小值.
评析和思考以二次函数为背景的函数最值问题是高一数学学习中一个重点内容.教师在进行教学设计时,将预设的题目变为引导学生自行研究、小组讨论、解题和归纳的开放题,让学生自己命制求函数最值的题目,顺着第一个学生的思维,组织学生进行自编活动,共编制出8个变式题.通过这样顺“思”而为的活动引导学生主动思考与探究,思维层层递进,将二次函数从“定轴定区间”的研究自然深入到“动轴定区间”“定轴动区间”“动轴动区间”的研究.在这样的过程中,学生的思维因问题的开放性和探究性而激活,教学效果必然好很多,同时,这样处理极大地调动了学生的积极性和主动性.从培养学生数学观念的角度看,这样的过程可以培养学生在一定的数学情境中抽象出数学概念、命题、方法和体系,积累从特殊到一般的活动经验、从静止到变化的函数思想方法,养成在日常学习和实践中从一般性角度思考问题的习惯,把握事物的本质,以简驭繁,运用数学思维思考并解决问题.顺“思”而为激发了学生的主动学习,实现了学生的思维升华,提升了学生核心素养发展,促进了学生的主动学习.
2 借“思”而上,探究知识本质,促进学生乐于学习
案例2等比数列前n项和Sn=a1+a1q+a1q2+…+a1qn-1公式的推导.
生1:提取公因数a1.
生2:倒序加?倒序乘?
生3:特殊化,令Sn=1+2+22+…+2n-1,猜想Sn=qn-1.

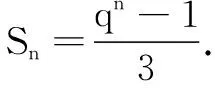


评析和思考很多教师在推导等比数列前n项和公式时将“错位相减法”硬塞给学生,学生表面上听懂了,但他们心中的“惑”由谁人来解?学生是在多次操练下似懂非懂地练“会”了,这是真的会了吗?他们理解为什么这样推导吗?学生对错位相减法的道理感觉云里雾里,整个学习处于被动的状态.
在讲授该内容时,笔者曾遇到这样的情景:先问学生如何进行推导,得到的回复是“我不会”,也有回答“错位相减法”的、再追问时得到的回答是“课本上就是这样”,然后顺着学生的回答讲授该方法,学生也就被动地听之.直到两年前,同样讲授该内容时,遇到一个“固执”的学生追问“为何如此推导”,且有不达目的不罢休之势,借着这位学生的“思”引导全班学生共同思考、探究,把顺势和借思的时间给足学生,终得上述案例2.
笔者曾做过多次调查,让高三的学生证明课本中一些定理、公式时,能证明或推导出的学生寥寥无几.课程改革致力于培养学生的核心素养、关键能力和终身学习的学习力,其出发点和根本目的是完全正确的,但是在教学实践中很多教师还是“新瓶装旧酒”,教学中仅仅关注“是什么”而忽视“为什么”,这不得不令人深思.实际教学中,我们完全可以把课堂真正让给学生,把思考的时间和机会留给学生,让学生借“思”而上.通过自己的理解和与同伴的交流讨论,学生一定能理解“错位相减法”的本质,其学习的兴趣也就自然被激发出来了.
3 因“思”利导,提升思维品质,促进学生深度学习
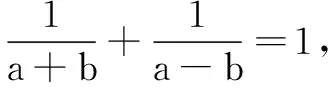
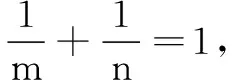

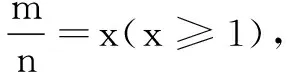
生5:也不对!因为当x=1时,m=n,即a+b=a-b,于是b=0,与已知条件矛盾.
生7:可以将题目改为求3a+2b的取值范围.
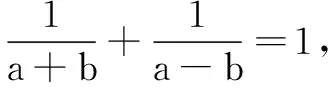
评析和思考在该案例中,从高考常考的多元最值问题出发,引导学生对问题进行多维的探究与反思,思维在交流碰撞中提升,真正理解了问题的处理方法.学生经历由通性通法研究到错误引发的思维过程,再到找到原因、变式研究,有效地巩固了数学知识、训练了解题方法、提升了解题技能、渗透了数学思想方法、提高了探究能力,这就是培养学生核心素养和关键能力的有效途径.高中数学知识方法千万条,但数学理解是第一条.课堂教学应立足于学生的“最近发展区”,以学生的眼光组织开展数学教学,最大限度地促使学生学会数学思考,提高数学思维的参与度.[2]
4 结语
在课堂教学中,我们不能只“授业”,而不“解惑”;不能只训练方法,而忽视能力的提升;不能只关注远方,而忽略了脚下行走的路;不能只关注“正确的”,还要多关注那些“错误的”;不能“硬塞给”学生,而应该吸引他们“过来拿”;不能将“台阶”都铺设好,而应该让学生自己搭建阶梯;不能只关注课前预设,更需要注重课堂生成,顺“思”而为,借“思”而上,因“思”利导,真正促进学生学会学习.

