充电桩三相AC/DC双向变换器控制策略研究

施文烨 何志琴 朱佑滔

（贵州大学，贵阳 550025）

主题词：充电桩 双向变换器 空间矢量脉宽调制技术 有源功率因数校正 建模仿真

1 前言

近年来，新能源汽车发展迅猛，但目前仍然面临着许多技术瓶颈，如充电桩的充电效率、电能质量以及只能被动单向充电等。文献[1]研究表明，不同的充电桩结构对电能的质量有很大影响。文献[2]研究表明，三相电流型脉宽调制（Pulse Width Modulation，PWM）整流器输出的直流电压低于输入电压的峰值，且由于输入电流不连续，其功率因数较低。文献[3]阐明，传统整流装置的功率因数通常在0.45～0.75 范围内，所以传统大功率整流器所产生的谐波会严重影响电网的电能质量。文献[4]提及，J.W.Kolar 教授提出了三相VIENNA 整流电路，虽然实现了升降压输出，但其开关损耗较大，同时不能实现电能的双向变换，控制电路的参数设计较为困难。文献[5]所研究的T 型三电平电路具有中点续流的能力，降低了开关导通损耗，改善了输出纹波且可以实现电能的双向流通，但其主电路结构和控制电路较为复杂，开关元器件较多，内管应力较大。文献[6]～文献[10]提到，对于混合微电网而言，连接交流母线和直流母线的AC/DC 双向变换器对系统电压的稳定和电能质量的提高产生了巨大的影响。针对上述问题，本文提出一种三相AC/DC双向变换器，给出在整流和逆变2种模式下的数学模型和空间矢量脉宽调制（Space Vector Pulse Width Modulation，SVPWM）控制策略，并利用MATLAB/Simulink搭建仿真模型验证该方案的可行性。

2 三相AC/DC双向变换器数学模型

图1所示为三相AC/DC双向变换器的拓扑结构，其中，、、为网侧三相电压，、、为网侧三相电流，为电路等效电阻，为网侧电感，、分别为直流母线电压、电流，为直流侧滤波电容，为负载电阻。在整流模式下（逆变模式过程相同），三相静止坐标中的数学模型为：

图1 变换器电力拓扑结构

式中，S(=a,b,c)为各相上、下桥臂的导通状态，S=1 为上桥臂导通，S=0为下桥臂导通。

将式（1）简化，再经派克（Park）、克拉克（Clark）变换后得到其在同步旋转坐标系下的数学模型为：

式中，为坐标系的旋转角频率；u、u、i、i分别为电压矢量、电流矢量在、轴上的分量；S、S分别为导通状态在、轴上的分量。

在u和u中存在、分量互相耦合，不利于控制器的设计，故需对式（2）进行拉普拉斯变换：

式中，U、U分别为电压外环的有功指令电压和无功指令电压；E()、E()、I()、I()分别为uS、uS、i、i的拉普拉斯变换结果。

对式（3）进行前馈解耦后，设在旋转坐标系下电压指令公式为：

结合式（1），为了消除ωLi、ωLi、E和E的影响，简化设计，将式（4）改写为：

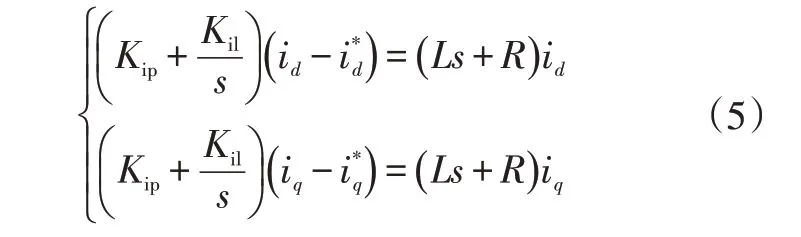
由式（5）可知，、分量已完全分解，只需确定PI调节器的和，即可实现其对电流内环的控制。

3 三相双向变换器有源功率因数校正控制策略

3.1 矢量合成基本原则

有源功率因数校正（Active Power Factor Correction，APFC）技术是将时变的交流量通过Park、Clark 变换为、分量并使用SVPWM 算法，最终实现电能的双向变换。由图1，在整流模式下，网侧输入三相电压的数学模型为：

式中，=2π为相位角初始值；为相电压的有效值；为交流电压频率。

则三相电压合成空间矢量()的表达式为：

由式（7）可知，()是旋转的空间矢量，幅值为相电压的1.5 倍，并按逆时针方向以角频率=2π匀速转动。根据电路上、下桥臂的导通状态可形成8 种组合，即6 个非零矢量和2 个零矢量，由式（7）可得到8个基本矢量的幅值及其所在矢量平面内的相位，如图2 所示。

由图2可知，系统被划分为6个扇区，每个扇区内的合成矢量都可由～合成。

图2 空间电压矢量分布及合成

3.2 矢量作用时间

以第1扇区为例，电压空间矢量的合成与分解如图3所示，由图3推导可知：

图3 电压空间矢量在第1扇区的合成与分解

式中，U和U分别为相电压的模在两相静止坐标系轴和轴上的投影；、分别为相邻作用矢量、的作用时间；为合成矢量的作用时间。

将式（8）简化后得到扇区内矢量的作用时间为：

通过以上推导可知，开关管存在同时导通和关断的情况，经过分析，只需通过调整驱动程序即可解决，不需要额外加死区时间避免直通。上述矢量合成的方法同样适用于逆变模式。

4 PI控制器参数设置

图4 所示为整流模式下矢量控制系统结构。在旋转坐标系下，由式（2）可知，U与U之间存在相互耦合，所以应采取前馈解耦控制，并采用PI 调节器进行调节，从而实现轴与轴的独立控制，提高系统动态性能。

图4 矢量控制结构

前馈解耦后由式（5）分析可得，在实际分析中，还需考虑电流采样延时和变换器本身的时间常数等影响，电流内环结构如图5所示，其中为PWM波形的增益。

图5 电流内环结构

按Ⅰ型系统设计，尽量使PI 调节器的零点与电流控制传递函数的极点相消，令=/τ，τ=/，同时，将图5 中的电流采样周期合并，并考虑阻尼比=0.707的Ⅰ型系统的二阶最佳系统，经校正，结合电流环的开环传递函数，可确定和，其具体表达式为：

将式（10）代入其闭环传递函数，可得：

最后考虑开关频率及的取值，式（11）可简化为：

由以上分析可知，只要系统的开关频率足够高，电流内环即可得到快速动态响应，本文的开关频率为10 kHz，所以响应速度已得到满足。

在整流模式下，开关管的通断频率远大于网侧电动势基波频率，故可以忽略PWM谐波分量，只考虑开关函数的低频分量，因此开关的函数表达式为：

式中，为PWM调制比。

整流模式下系统交流侧的电流为：

式中，为相电流的有效值，则对应直流侧输出为：

将式（13）和式（14）代入式（15），经简化可得：

则其电压外环控制结构如图6 所示。电压外环PI控制器的主要作用是稳定直流侧的输出电压，故从抗干扰角度出发，选用Ⅱ型系统，由图6 可得电压环的开环传递函数()为：

图6 电压环控制结构

式中，为系统电压环的位置误差系数；为系统电压环的指数系数；为系统电压环随机选取的周期。

在图6 中，i为电感电流。又由电压外环频宽=/，根据工程设计方法中Ⅱ型系统参数计算公式可得：

在实际工程应用中，系统的抗干扰和系统跟随性都会综合考虑电压外环频宽=5，将其代入式（18），可得电压外环PI调节器的比例和积分系数分别为：

式中，为系统电压环的静态速度误差系数；为系统电压环PI 调节时间；为系统电压环总的作用时间。

经上述分析确定了电流电压外环PI 控制参数，减少了试验中参数选择的盲目性，但在实际应用中，由于设备参数不统一，还需根据实际情况进行微调，以求得最优参数取值。经过验证，整流模式下PI 控制器参数的确定方法同样适用于逆变模式。

5 仿真与结果

本文针对三相AC/DC 双向变换电路，采用前馈解耦的双闭环控制策略和SVPWM 的调制策略来控制功率开关管通断，利用MATLAB/Simulink仿真软件平台搭建仿真模型，如图7所示。

图7 系统在不同模式下的仿真模型

仿真参数设置为：交流侧相电压=220 V，频率=50 Hz，直流侧输出电压=400 V，输出功率=4 kW，开关频率=10 kHz，交流测电感=3.3 mH，电路等效电阻0.05 Ω，直流侧滤波电容=1 200 μF。仿真波形如图8 所示。

图8 系统在不同模式下的仿真波形

由图8a可知，系统起振初期，因直流侧接了较大的滤波电容，输入电流呈现出较大的电流过充。持续约0.02 s后，输入电压与电流保持同相位，实现系统在整流模式下在单位功率因数状态运行。由图8b 可以看出，外环电压经过PI调节器能够敏锐地追踪外观指令电压（400 V），调解时间约为0.02s，实现输出电压的稳定追踪，且输出的电压和电流可根据电池的充电需求随时调整。由图8d可知，电流呈正弦波且与电压同相位，符合相关并网技术标准。

图9 所示为整流模式下交流侧的谐波分析结果，在整流模式下交流侧的总谐波失真（Total Harmonic Distortion，THD）为0.87%，远小于5%，电能质量所受干扰明显减小。图10所示为逆变模式下交流侧的谐波分析结果，逆变模式下的总谐波失真为3.12%，可以看出，变换器的电流谐波含量低，实现了变换器高功率因数运行。对比文献[3]和文献[5]，该拓扑结构的总谐波失真明显降低。

图9 整流模式下交流侧的谐波分析

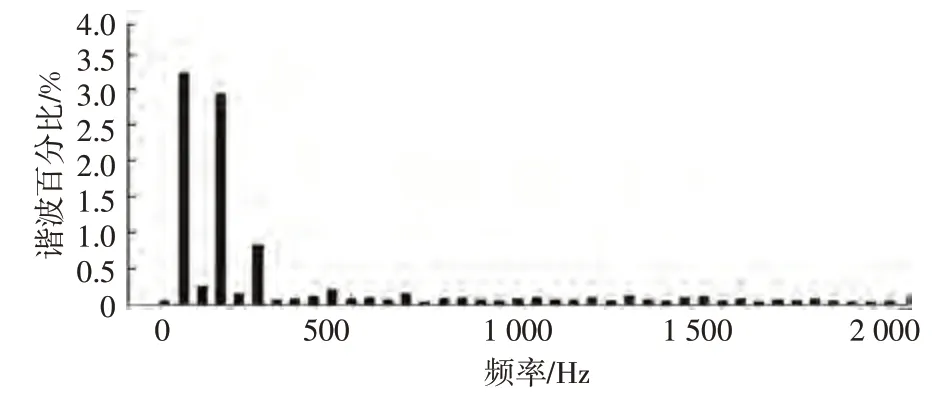
图10 逆变模式下交流侧的谐波分析

对试验样机进行相应试验，图11所示为原理样机，图12所示为上电后功率开关管的驱动信号。

图11 试验原理样机

图12 功率开关管的驱动信号

系统在整流模式下的输入、输出波形如图13 和图14所示。

图13 输入三相电压波形

图14 输出电压值

系统在逆变模式下的输入、输出波形如图15 和图16所示。

图15 输入电压值

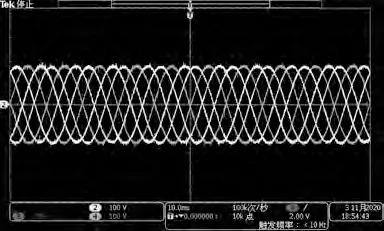
图16 输出电压波形

系统的功率如图17 所示，通过对比图15 得出系统的传输效率为96.44%，对比文献[3]和文献[5]，效率均有所提升。

图17 输出功率

6 结束语

本文提出了一种三相AC/DC 双向变换器拓扑结构，并提出了相应的SVPWM 调控策略，通过引入有源功率因数校正技术，使得系统能够在单位功率因数下运行，并减少了电网谐波，能够实现能量的双向流动。经分析，变换器无直通问题，可以不外加死区，直流侧电压可调，减少了变换器对于电能质量的影响，并通过MATLAB/Simulink 仿真平台验证了该方案的可行性及优势，最后利用原理样机进行试验，结果表明，系统可实现电能的双向变换、高功率因数运行，并进一步提高了电能的传输效率。