基于导波原位检测的复合材料疲劳表征与寿命预测研究

姚卫星，张超，黄宇翔，陶翀骢，裘进浩，马铭泽

（南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016）

0 引言

目前，纤维增强复合材料（Fiber Reinforced Plastic，简称FRP）因其高比刚度、高比强度和良好的抗腐蚀性能被广泛地应用于航空航天飞行器，其材料的结构重量百分比已成为衡量飞行器先进性的重要指标之一。为了降低结构重量、充分发挥复合材料承载潜力，提高飞机结构中的复合材料许用应变是未来发展的必然趋势。但是，随着许用应变值的提高，复合材料疲劳问题就会逐渐显现，从而威胁结构的安全性能。在飞行器复合材料结构设计和使用的过程中，利用先进的无损检测手段表征复合材料全寿命周期中力学性能的变化，实现复合材料疲劳状态评估和疲劳寿命预测，不仅能够保障飞行器服役安全、提升经济效益，还可以减少低许用应变对设计余量带来的压力，充分发挥轻量化优势。

近年来，基于检测数据的复合材料结构的疲劳表征与寿命预测已成为研究热点，其中基于复合材料强度、刚度的疲劳衰退模型在试件级的单轴拉伸试验中已得到了验证。万志敏等认为剩余刚度服从Weibull分布，并且建立了剩余刚度和剩余强度及寿命的关系模型；冯培锋等从唯象的角度提出了复合材料疲劳剩余刚度衰退模型，研究了常幅疲劳载荷下的复合材料刚度衰退规律，建立了基于加载寿命比的结构刚度衰退统计分布模型。然而，以拉伸的方式测量材料刚度的方法难以在实际飞行器中应用，且疲劳引起的结构局部性能衰退难以充分得到表征。因此，亟需开展适用于原位无损测量的复合材料寿命预测方法的研究。在众多无损检测方法中，基于导波的检测技术以其穿透能力强、对微小损伤敏感、能够实现非接触原位无损测量等优势，在复合材料损伤检测与疲劳评估的应用中具有较大潜力。N.Toyama等研究了基体开裂程度对导波波速变化的影响，并证明了波速的原位测量可以用于评估层合板的裂纹密度；A.Mardanshahi等在实验中测得了多组不同裂纹密度下复合材料中的导波数据，发现其传播幅值、速度随载荷周期的增加呈下降趋势；W.Li等研究了复合材料板在热疲劳载荷和加湿条件下的导波相速度变化，发现湿度增加和循环热载荷都会导致导波速度下降。在复合材料疲劳寿命预测方面，研究者在已有的疲劳机理研究基础上，进一步应用人工智能算法开展相关研究。廖兴升等在提出用频率表征玻璃纤维复合材料层合板刚度下降的基础上，采用高斯正态分布的疲劳损伤仿真模型，用获得的频率衰减曲线对神经网络进行训练，实现了剩余寿命的预测；A.Vassilopoulos等针对多向玻璃纤维复合材料，利用人工神经网络模型预测了不同铺层、应力比和加载模式下的寿命曲线；P.A.Kulkarni等结合非线性自回归神经网络模型和基于长短时记忆的递归神经网络模型，实现了多环境参数的风速预测和疲劳寿命预测。现有的应用人工智能技术的复合材料寿命预测研究主要针对结构刚度等特征展开，应用导波特征的复合材料寿命预测鲜有研究。

为了发挥导波原位无损检测技术的优势，实现利用导波进行疲劳检测与寿命预测，本文从宏观和细观的角度研究复合材料疲劳损伤演化规律；在此基础上，分析疲劳损伤累积对导波相速度以及导波模态转换的影响规律；以数据驱动的方式对复合材料疲劳程度进行表征，并基于贝叶斯模型平均方法的疲劳演化模型实现复合材料疲劳寿命的预测。

1 基于非接触式测量的飞行器复合材料结构寿命预测技术框架

复合材料结构在循环载荷作用下会产生不同程度的损伤萌生、扩展和累积，进而导致整体力学性能的退化。而损伤的出现和材料特性的变化将引起导波特征的改变，使得导波特征中隐含了疲劳程度信息。因此，通过导波数据的无损测量能够实现复合材料疲劳状态的表征。为了实现飞行器安全保障和单机定寿的目标，本文提出基于非接触式测量的飞行器复合材料结构寿命预测技术框架，如图1所示，总共分为4个部分。利用激光超声技术的非接触式测量优势，以原位无损检测的手段获取大量飞行器结构中整体/局部的导波数据；利用先进信号分析方法批量处理导波数据，提取对疲劳敏感的导波特征，并对多导波特征进行融合处理；结合人工智能的技术手段，以大量导波数据为驱动，构建整体部件疲劳演化数字孪生模型作为寿命预测的模型；同时，获取服役过程中的载荷和环境信息，作为模型的输入参数，利用测得的导波数据作为反演整体/局部材料疲劳特性的因子，更新模型中的疲劳演化参数，最终，实现复合材料整体部件的视情寿命预测。在此框架下，本文针对复合材料结构疲劳损伤演化规律、疲劳损伤累积对导波传播的影响以及应用导波特征的复合材料疲劳评估与寿命预测开展相关研究工作。

图1 基于导波测量的复合材料寿命预测框架Fig.1 Framework for fatigue life prediction of composite materials based on guided wave measurement

2 复合材料结构疲劳损伤演化机理及模型

复合材料疲劳过程中疲劳损伤包括微尺度损伤以及宏观可见损伤，疲劳损伤的演化过程是从微损伤向宏观损伤进行发展的，如图2所示。复合材料中的微损伤主要包括基体中的微裂纹、局部的纤维断裂和基体—纤维脱粘，宏观损伤则由层间分层以及面内的宏观断裂构成，包括冲击损伤和微损伤扩展产生的大分层等。

本文分别从宏观唯象和细观物理的角度研究复合材料疲劳损伤演化规律，提出复合材料的剩余刚度模型。

图2 复合材料典型损伤演化规律示意图Fig.2 Schematic diagram of fatigue damage evolution of composite materials

2.1 宏观唯象模型

纤维间破坏主要表现为弥散型基体裂纹。由于横向基体裂纹密度与结构纵向刚度呈线性关系，基体裂纹密度与寿命比可用单参数幂函数进行描述；纤维随机断裂和分层主导了阶段Ⅱ刚度下降，这一阶段剩余刚度和载荷循环数服从线性关系。复合材料内部的疲劳损伤是阶段Ⅰ和阶段Ⅱ的损伤总和，因此得到剩余刚度演化规律，如图3所示。

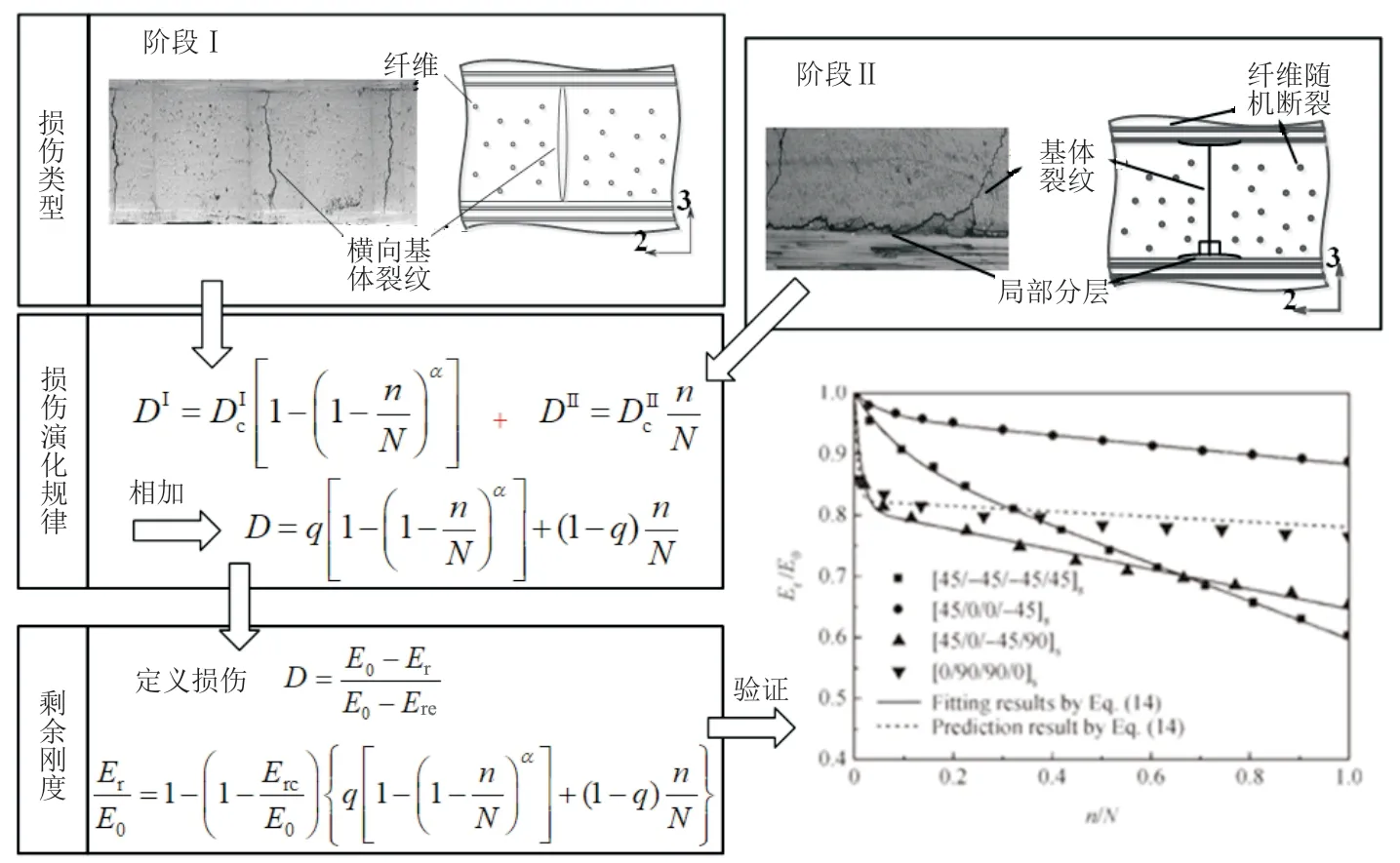
图3 剩余刚度演化规律和试验验证［13］Fig.3 Evolution law of residual stiffness and experimental verification［13］

2.2 细观物理模型

疲劳载荷下的复合材料层合板多向损伤力学模型的框架如图4所示。模型基于疲劳载荷下的物理损伤机理，将根据试验结果得到的材料基本力学性能参数与损伤演化参数作为模型的输入参数，包括损伤表征模型以及损伤演化模型两个部分，分别研究基体裂纹损伤对材料多个方向上力学性能的影响以及损伤在疲劳载荷下的演化规律。损伤表征模型中给出表征模型在不同载荷类型下的适用性，并最终得到含基体裂纹损伤的本构方程。损伤演化模型中则基于Paris公式以及微观损伤力学方法推导得到层合板内开裂层的初始裂纹萌生寿命方程，并根据该方程建立疲劳损伤累积框架用于预测疲劳载荷下的复合材料层合板内横向基体裂纹损伤的演化规律。此外，模型同样考虑了疲劳载荷下三种主要因素对损伤演化的影响。基于建立的多向损伤模型预测得到疲劳载荷下的复合材料层合板的损伤演化规律以及刚度退化规律，并将试验结果与模型预测结果相对比以验证模型的有效性，如图5～图6所示。

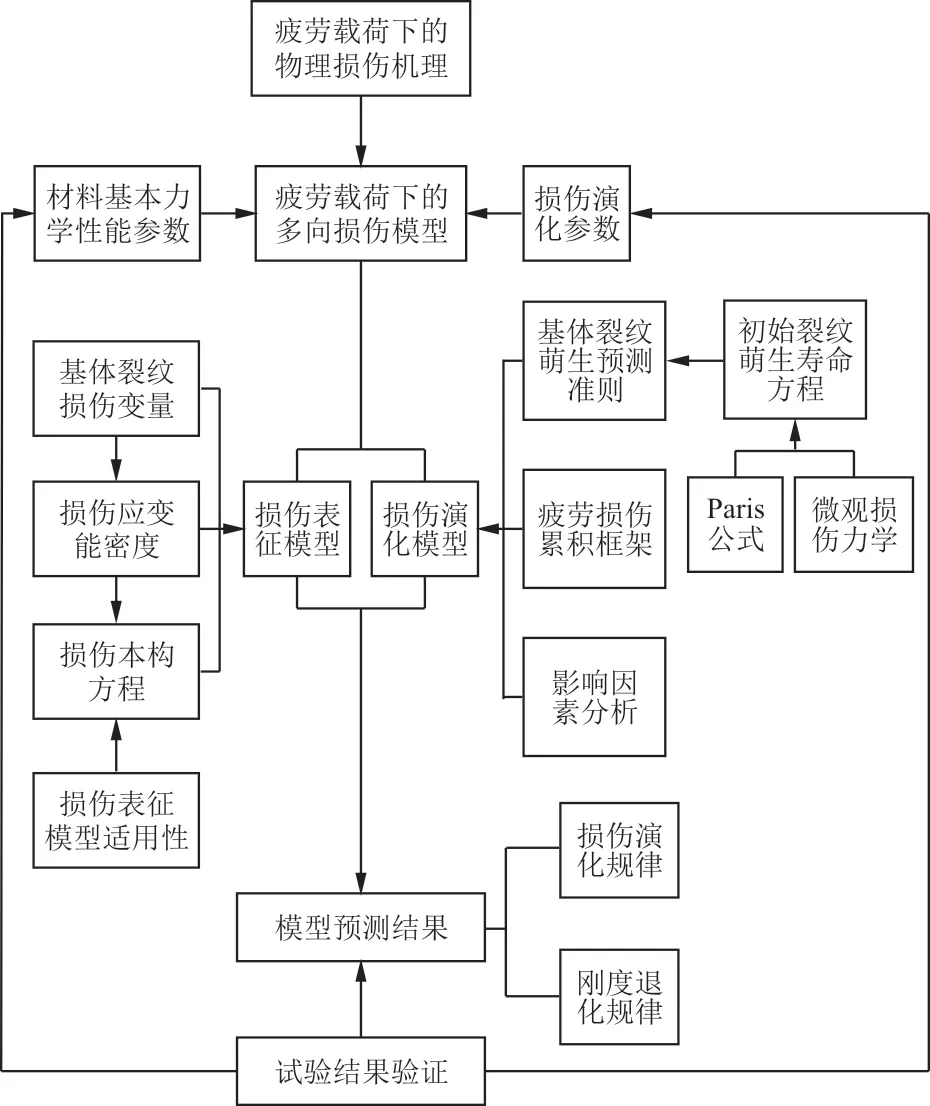
图4 疲劳载荷下的复合材料层合板多向损伤力学模型框架［14］Fig.4 Multidirectional damage mechanics model framework for composite laminates under fatigue load［14］

图5 基体裂纹密度演化预测结果与试验结果［15］Fig.5 Prediction and test results of the evolution of matrix crack density［15］

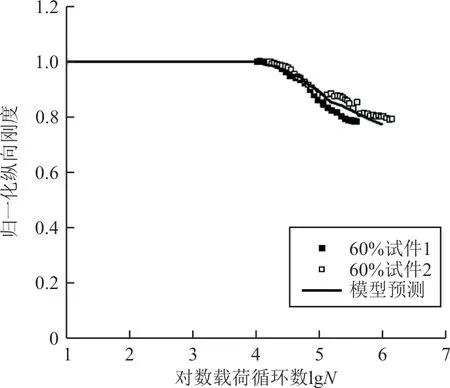
图6 纵向刚度演化预测结果与试验结果［15］Fig.6 Prediction and test results of the evolution of longitudinal stiffness［15］

3 疲劳损伤累积对导波传播的影响机制

3.1 复合材料疲劳引起的导波模态转换规律

为探究导波受复合材料疲劳损伤累积的影响规律，利用疲劳拉伸机和激光超声检测系统进行实验研究。疲劳实验拉伸加载过程中载荷水平为静强度的60%，载荷应力比设为0.1，加载频率为8 Hz。为了获取试验件在疲劳累积过程中的刚度变化，使用引伸计监测试件的变形情况，如图7所示。在拉伸过程中，激光超声检测系统通过激光器发射出高能激光并照射到待测结构中，由于热弹效应的作用，结构中会生成沿表面传播的导波，进而利用AE传感器对结构中传播的导波信号进行采集，即可获得包含疲劳损伤信息的导波波场。

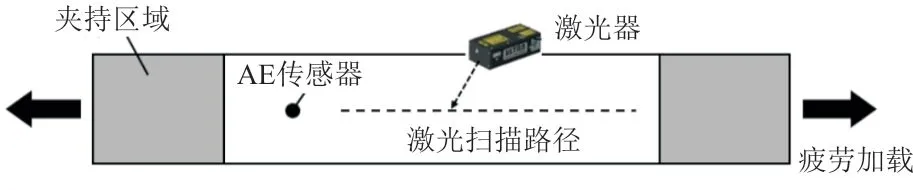
图7 疲劳拉伸与激光超声检测示意图Fig.7 Schematic diagram for fatigue test and laser ultrasonic test

由于在采集到的原始时间—空间域波场中较难分辨导波模态信息，使用二维傅里叶变换，将时间—空间域波场转换到频率—波数域波场中。疲劳加载过程中频率—波数域波场的演化过程如图8所示，可以看出：随着疲劳加深，对称模态（模态1）能量逐渐减小，反对称模态（模态2）能量不断增大。

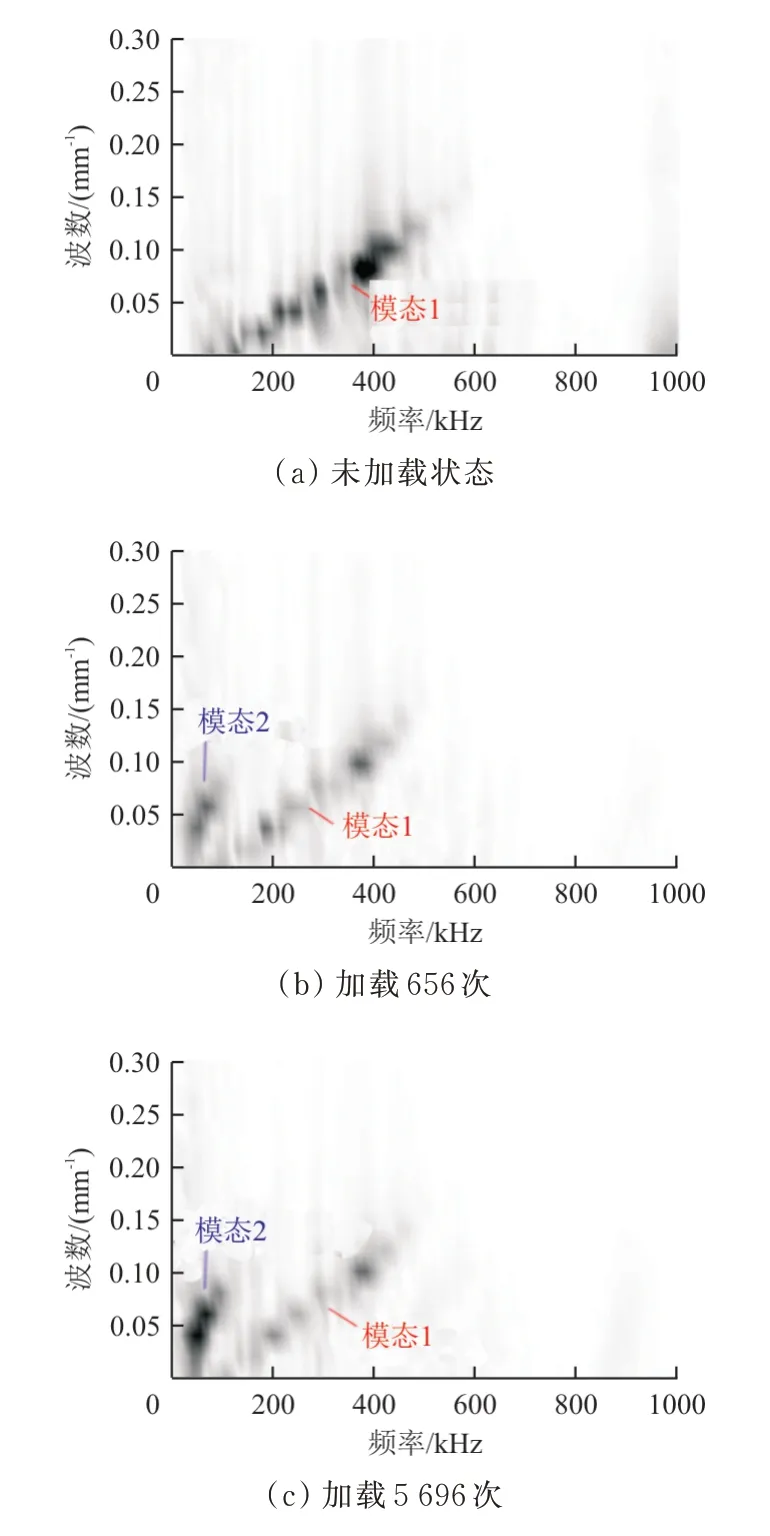
图8 不同载荷周期下的导波频率—波数域波场图Fig.8 Frequency-wavenumber diagrams of the guided wave with different load cycles

为建立模态能量分布的变化与疲劳的关系，定义模态1与模态2的能量比对模态转换进行量化。不同加载应力水平下的归一化后的值、拉伸模量和导波相速度随疲劳周期数变化曲线如图9所示，可以看出：随着疲劳损伤的加深，值逐渐下降，且相比于拉伸模量和导波相速度，的下降趋势更加显著。尤其在疲劳前中期，下降速率明显更快，体现出其对疲劳更强的敏感性。实验结果与仿真结果一致，验证了利用模态转换评估复合材料疲劳的潜力。

图9 归一化IMC值、拉伸模量、导波相速度随疲劳周期数变化曲线Fig.9 Curves of normalized IMC，tensile stiffness and guided wave phase velocity against fatigue load cycles

3.2 复合材料疲劳引起的导波相速度下降规律

在频率较低情况下，结构刚度与对称模态相速度近似呈平方关系，因此可以开发一个能同时适用于结构刚度与导波对称模态相速度的疲劳衰退模型。为了使刚度/相速度退化模型符合复合材料实际损伤机制，需要明晰不同的损伤模式对结构刚度的影响。在实验中，发现第一个加载周期内由于纤维断裂导致的刚度跳跃，可以使用一个简单的纤维损伤因子来评估。

式中：E为一个加载周期后的刚度；为健康结构的刚度；为纤维损伤因子。

针对基体裂纹，利用简化关系近似估计裂纹密度和剩余刚度之间的关系：

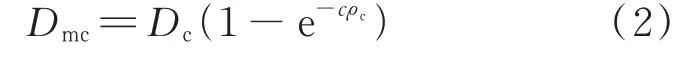
式中：为与材料参数相关的系数；为基体裂纹密度；为量化基体裂纹的损伤变量；为刚度衰减平缓阶段结束时的损伤变量。

本文认为分层损伤附属于基体裂纹，可以通过一个系数来体现这一附属关系：

式中：为分层损伤因子；为一值较小的附属系数。

上述附属关系体现出分层损伤伴随基体裂纹的产生而出现，且分层损伤对结构刚度的影响较小。进而，可以合并两种损伤形式：

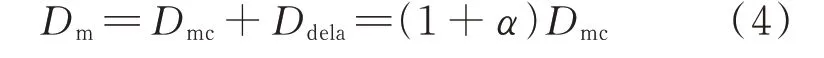
结合剪滞近似模型与Paris定律，获得基体裂纹损伤因子的演化率：

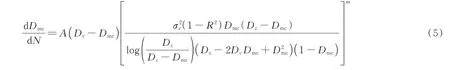
其中，

式 中：和为Paris经 验 参 数；为 载 荷 比，=/；为与材料系数以及板结构构型相关的系数。

综合三种损伤形式，可以得到+1疲劳载荷周期下的总损伤因子。

总损伤因子主要包含两部分损伤：纤维损伤因子，融合基体裂纹和分层损伤的损伤因子。总损伤因子的影响参数有3个：、以及。

在此基础上，利用实验所得导波对称模态相速度数据对上述模型参数进行识别。识别的对象主要为纤维损伤变量，分层损伤附属系数以及Paris公式指数系数和幅值参数。其中可以使用一个加载周期后的剩余刚度或者相速度计算得到。分层损伤附属系数对损伤演化的影响较小，可以从1.01～1.10以步长0.1进行拟合试错，通过对比拟合结果的好坏来确定值。和可以通过对式（6）进行线性拟合得到，拟合结果的斜率值为系数，截距值为log。32.4%应力水平下［0°/90°/0°/90°］铺层层合板的刚度以及相速度曲线拟合结果与实验数据对比如图10所示，可以看出：使用该模型能够较为准确地描述刚度/相速度退化情况。

图10 ［0°/90°3/0°/90°3］s铺层层合板刚度和相速度退化拟合结果Fig.10 Fitting results of the degeneration of stiffness and phase velocity with the stacking sequence of［0°/90°3/0°/90°3］s

4 复合材料疲劳演化表征方法与寿命预测

4.1 基于深度学习的复合材料疲劳演化表征方法

传统复合材料疲劳表征方法中，需要应用大量力学知识构建复杂的演化模型。由于复合材料疲劳本身具有较大分散性，加上模型构建和求解的过程中，不可避免地需要对复杂模型进行大量简化，这极大限制了疲劳表征的准确度及其应用范围。近年来人工智能的发展为复合材料的疲劳演化建模表征提供了新的思路。

实验获得的在复合材料板中传播的导波波场图如图11所示，图中斜率即为导波传播相速度，可以看出：导波相速度受结构刚度影响，随着疲劳累积，结构刚度降低，导波相速度也会逐渐退化。利用卷积自编码器，可以自动对原始导波波场进行压缩降维并获取用于表征疲劳状态的特征。为扩充训练样本，仿真时从均匀分布函数（0.5，1.2）中随机生成比例系数作杨氏模量的权重，进而模拟复合材料在循环载荷下刚度退化引起的导波波场信号变化。为使提取的特征具有物理意义，应用物理信息约束来指导自动编码器提取与结构刚度相关的潜在特征。

图11 原始导波波场Fig.11 Raw guided wave field

提取出波场潜在特征后，需要使用模型来表征其随疲劳损伤累积的演化过程。本文提出的深度学习模型完整架构图如图12所示，考虑到疲劳试验期间施加在试样上的循环载荷因试样而异，同时复合材料的疲劳演化具有随机性，利用循环神经网络识别每个样本的模型参数。将模型参数输入至全连接神经网络中，通过形成一个常微分方程对潜变量的演化机制进行建模，提取波场特征的动态演化过程。

式中：为描述潜在特征演化的常微分方程。

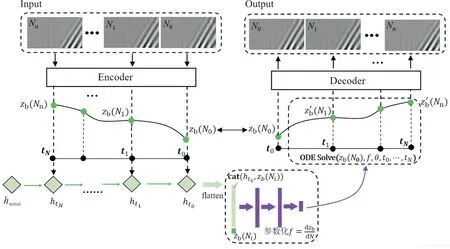
图12 深度学习模型完整架构图Fig.12 The deep learning architecture

根据文献［20］实验中的经验，复合材料的疲劳累积与加载载荷幅值、加载应力比以及复合材料自身属性有关。因此，式（8）可写成：

式中：为与试件自身状态与加载环境条件有关的模型参数。本文利用全连接神经网络作为函数近似器求解。

自编码器重构导波波场与实验测得波场对比如图13所示，图中红线为健康状态下导波波场斜率。

图13 重构波场与实验测得波场对比Fig.13 Comparison of reconstructed wave field with experimentally measured wave field

从图13可以看出：重构效果较好，自编码器网络能够提取出导波波场特征；疲劳加载后波场斜率开始偏离红色参考线，且随着加载周期数的增加，偏离量也逐渐增大。

神经网络训练得到的潜在特征与实验获取到的刚度损伤因子随疲劳积累演化对比如图14所示，可以看出：训练得到的潜在特征随疲劳积累演化与刚度损伤因子演化趋势基本一致，这表明深度学习模型能够自动地提取导波波场中与疲劳相关特征，并获取该潜在特征的动态演化信息。

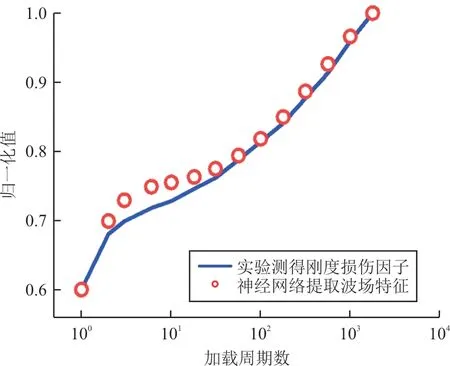
图14 神经网络训练得到的潜在特征演化Fig.14 The evolution of the latent wave field feature obtained from the neural network

4.2 基于贝叶斯模型平均方法的复合材料寿命预测

复合材料结构的刚度和强度是评判结构退化程度最为常见的力学性能指标，从而衍生出一系列基于剩余刚度和剩余强度的疲劳寿命预测模型。然而，对于服役中复合材料结构，材料的剩余强度和刚度通常难以直接测量。基于导波无损、非接触、快速的测量优势，利用对疲劳敏感的导波特征（如导波相速度等）能够以无损的形式实现复合材料疲劳寿命预测。

在获得如式（5）所示的仅考虑基体裂纹情况下的损伤因子演化规律基础上，将分层损伤视为基体裂纹的附属损伤，在同时考虑基体裂纹与分层的情况下，损伤因子的演化率可以表示为

在该简化下，刚度退化曲线随裂纹饱和逐渐平缓，不会持续下降，这与实验中观察到的刚度持续退化直至疲劳失效的现象不同。为修正这一点，提出一种具有独立分层系数的改进退化模型。

式中：为一个独立的分层系数；为一个调节参数，以确保分层造成的损伤在合理范围内。

为解释实验中第一次加载循环后出现的纤维断裂现象，损伤模型中包含了一个如式（1）所示的纤维损伤变量：

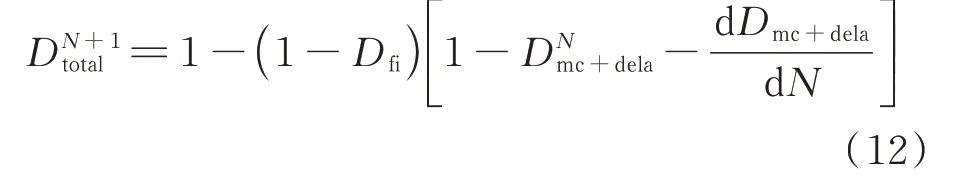
根据上述基于不同损伤机制的损伤因子演化模型构建5个子模型，记为S1～S5。其中，子模型S1为仅考虑基体裂纹的基础模型，如式（5）所示；S2为包含非独立分层系数的模型，如式（10）所示；S3与基础模型类似，但将设置成一个包含材料参数不确定性的推断参数；S4为具有独立分层系数的损伤模型，如式（11）所示；S5为S3和S4的组合。

将激光超声试验获取的对称模态相速度信息（或者刚度数据）转换为损伤因子，并提供给S1～S5各个子模型，同时采用序列蒙特卡洛的方法对模型参数的后验分布进行采样近似。在得到稳定马尔科夫链的基础上，采用留一交叉验证的方法对各个子模型的预测精度进行评价，并以该评价值为权值，对子模型进行加权平均，最终得到分层模型的平均贝叶斯分布。静强度的45%应力水平等幅周期载荷作用下，利用对各子模型加权平均后得到的波速/刚度退化模型对玻璃纤维增强复合材料采集到的刚度数据进行拟合的结果如图15所示。

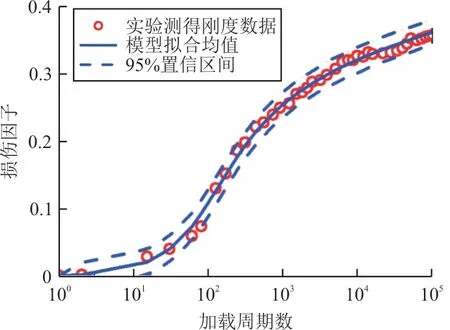
图15 45%载荷水平下结构刚度演化过程拟合结果Fig.15 Fitting results of the evolution of tensile stiffness under the stress level of 45%

从图15可以看出：应用贝叶斯模型平均方法能够较好地拟合刚度随疲劳演化过程。

在此基础上，进一步结合激光超声扫描实现GFRP层合板在疲劳载荷下的相速度数据采集，并通过不断更新相速度数据，评估模型对疲劳演化过程的预测能力。随着实验观察数据的增加，贝叶斯模型更新的过程如图16所示，可以看出：分层贝叶斯模型仍能准确地对导波相速度的下降行为进行表征，当更新输入数据较少时，疲劳演化预测结果相对实际值偏离较大，随着数据点的增加，置信区间明显缩小，模型的预测精度显著提高。在疲劳前期，模型以其先验经验和本身子模型是基于损伤机制的特点，对损伤的后续扩展行为做出了准确预测。

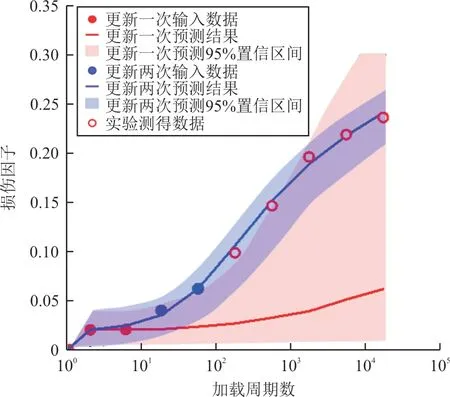
图16 基于导波相速度数据的贝叶斯模型更新过程Fig.16 Updating process of the Bayesian model based on phase velocity data

为了对复合材料结构寿命进行预测，本文利用基于置信区间的剩余寿命预测准则：给定一个预设的失效阈值，当预设置信区间上届达到该阈值时，认为该结构失效。采用贝叶斯模型平均方法和置信区间准则的疲劳寿命预测结果如图17所示，可以看出：利用相同载荷水平下的其他试件数据作为先验的预测结果明显好于无先验知识情况下的预测，仅在更新数据较少时，无先验知识的情况下未能对结构疲劳进行提前预测；随着更新数据的增加，疲劳寿命提前预测偏差有减小的趋势；应用贝叶斯模型平均方法和置信区间准则可以在试件寿命的前期获得较为稳定和保守的寿命估计。

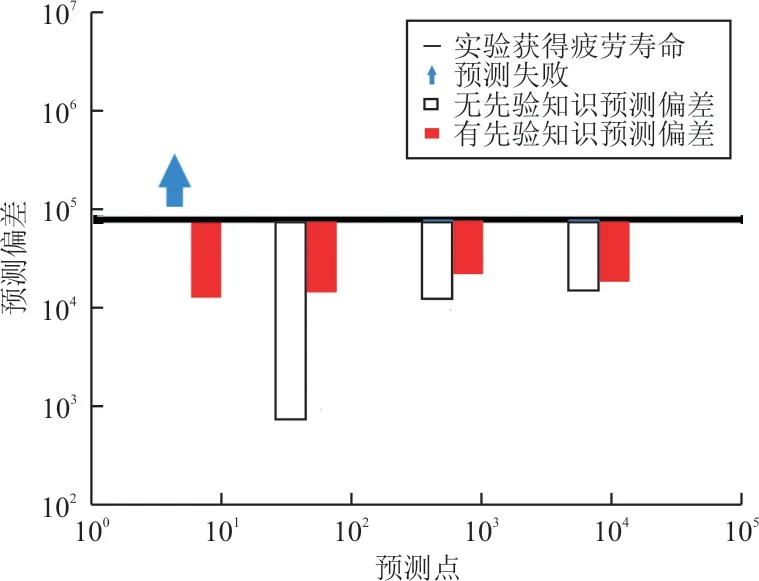
图17 应用贝叶斯模型平均方法和置信区间准则的寿命预测结果Fig.17 Fatigue life prediction results using Bayesian model averaging method and confidence interval criterion

5 结论

（1）考虑多种损伤模式，本文分别从宏观和细观的角度研究了复合材料疲劳损伤演化规律，给出了复合材料的剩余刚度模型。

（2）通过分析导波波场信息，揭示了利用模态转换效应进行复合材料疲劳表征的潜力。从复合材料损伤机理出发，建立了考虑纤维断裂、基体裂纹、分层三种形式损伤的刚度与导波相速度随疲劳演化模型，得到了疲劳载荷下的复合材料层合板的损伤演化规律以及刚度退化规律。

（3）构建了由卷积自编码器、循环神经网络和全连接神经网络组成的深度学习框架，实现导波波场中疲劳特征的自动提取。同时，提出了基于贝叶斯模型平均方法的疲劳表征模型，应用导波相速度特征，实现了复合材料剩余疲劳寿命的预测。