飞机薄壁结构面外载荷下三维疲劳裂纹扩展仿真分析

曾苇鹏，鲁嵩嵩，刘斌超，刘汉海，隋福成，鲍蕊

（1.北京航空航天大学 航空科学与工程学院，北京 100083）

（2.中国航空工业集团有限公司 沈阳飞机设计研究所，沈阳 110035）

0 引言

薄壁结构是飞机的基本结构形式之一，是飞机设计时用来承受面内的拉伸和剪切载荷的重要结构。然而，部分薄板结构在实际应用中，不可避免地要承受面外弯曲载荷，由于薄板结构的抗弯截面刚度很小，面外弯曲载荷会引发极大的弯曲应力，进而影响此类结构的使用寿命。例如，某型飞机服役过程中，来自锁钩和锁环的集中载荷，将导致座舱盖相关侧型材薄板结构发生面外弯曲，从而承受较高水平的面外弯曲载荷。由于飞机服役中的载荷环境具有交变的特征，此类面外弯曲载荷将导致侧型材薄板结构存在较大的疲劳失效风险，进而影响飞机的使用安全。因此，有必要对面外弯曲载荷下的薄板结构开展疲劳/损伤容限评定。

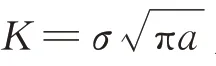
随着计算机软硬件水平的提升，数值模拟成为分析裂纹问题的有力手段。I.S.Raju等基于有限元计算结果，给出了拉伸或弯曲载荷下半椭圆表面裂纹应力强度因子随参数角度、裂纹深度、裂纹长度、板厚和板宽变化的经验公式，并分析了板宽对裂纹前缘应力强度因子变化的影响；X.B.Lin等采用有限元方法计算应力强度因子，模拟了裂纹扩展，并讨论了敏感性和网格非正交对应力强度因子的影响。

目前，以有限元为代表的各类数值仿真方法已经基本解决了各类裂纹的应力强度因子计算问题。部分构型与承载简单的结构的裂纹扩展模拟问题也已基本解决，但复杂裂纹的裂纹扩展模拟研究仍有待继续深入。为了模拟复杂裂纹的裂纹扩展，研究人员开发了三维裂纹扩展分析软件FRANC3D，且已有许多研究者利用该软件进行了不同结构在部分承载形式下的裂纹扩展模拟研究，并验证了FRANC3D计算的可靠性和准确性。但这些研究大多是针对单向或双向拉伸载荷进行的，针对弯曲载荷下的薄板结构的研究较少。

本文针对面外弯曲载荷下的裂纹扩展分析方法开展研究。采用将弯矩等效成拉应力的方法，计算面外弯曲载荷下疲劳裂纹的应力强度因子，并分析该等效方法的准确性；采用FRANC3DABAQUS联合仿真的方法，模拟疲劳裂纹扩展，得到面外弯曲载荷下板的裂纹扩展特征；在此基础上分析影响应力强度因子计算结果的因素，讨论仿真方法的适用性。

1 基于弯矩等效拉伸应力方法的薄板应力强度因子计算

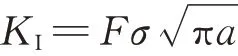
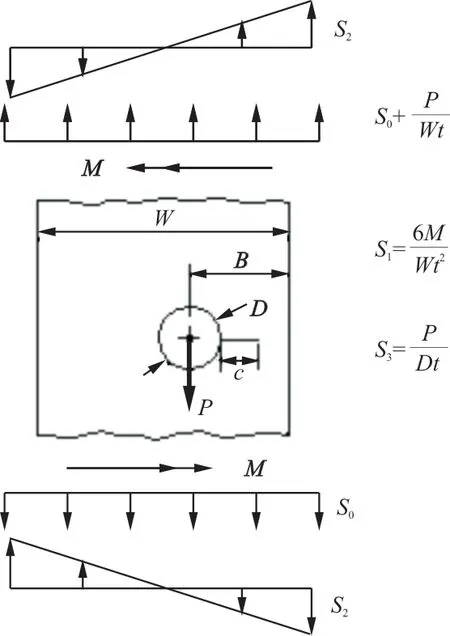
图1 NASGRO中的等效拉伸载荷方法［16］Fig.1 Equivalent tensile load method in NASGRO［16］

将此等效方法用于中心带孔板（长230 mm、宽300 mm、厚3 mm、圆孔直径6 mm、初始裂纹总长12 mm，如图2所示）的应力强度因子计算。由于此板仅受弯曲载荷作用，在采用此方法计算等效拉伸应力时，仅考虑部分。对应的几何修正因子的数值可在应力强度因子手册中查表得到，其值接近1。

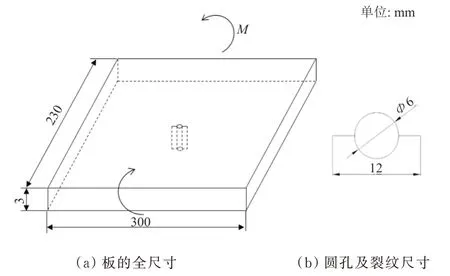
图2 中心裂纹板尺寸及受载情况Fig.2 Size of central crack plate and the applied load

等效方法的应力强度因子计算结果与文献［1］中的试验结果对比如图3所示，可以看出：等效方法的应力强度因子计算结果明显偏大（大于100%）。因此，该等效方法不适用于弯曲应力占主导地位的应力强度因子计算。

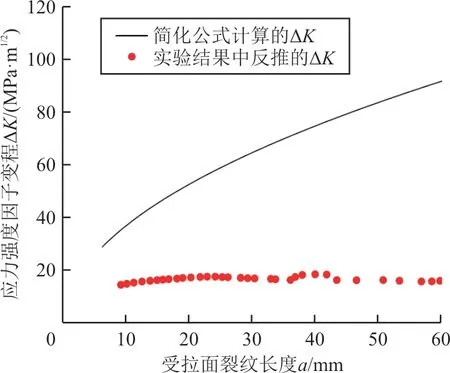
图3 等效公式和试验［1］反推的应力强度因子变程Fig.3 Stress intensity factor variation from simplified formula and experiment［1］

2 仿真与分析

2.1 FRANC3D与ABAQUS联 合 仿 真 流 程

FRANC3D与ABAQUS联合仿真的具体流程为：在FRANC3D中导入无裂纹的有限元模型，使用FRANC3D提供的功能插入指定位置和形状的裂纹，FRANC3D对插入裂纹的有限元模型重新划分网格；再调用ABAQUS求解有限元模型，FRANC3D利用ABAQUS的计算结果，计算裂尖裂纹扩展驱动力，即应力强度因子，判断是否达到断裂韧度，如果达到了则停止裂纹扩展，如果没达到，则根据应力强度因子计算裂纹扩展后的前缘；重复从重新划分网格到扩展裂纹前缘的过程，使裂纹不断扩展。仿真流程图如图4所示。

图4 FRANC3D与ABAQUS联合仿真流程Fig.4 FRANC3D and ABAQUS joint simulation process

FRANC3D的主要作用是重新划分裂纹前缘周围的网格、计算应力强度因子以及计算裂纹前缘扩展。FRANC3D在计算应力强度因子时，提供了-积分、虚拟裂纹闭合技术等方法。在获取裂纹前缘各节点的应力强度因子后，FRANC3D采用最大周向应力准则或其他准则判断裂纹的扩展方向，并采用Paris公式或其他裂纹扩展速率公式，计算一定循环次数后裂纹前缘各节点的扩展方向和扩展距离，并对扩展后的节点进行曲线拟合，得到扩展后的裂纹前缘。

2.2 基于有限元仿真的应力强度因子计算

中心带孔板的有限元模型如图5所示，模型尺寸同图2。

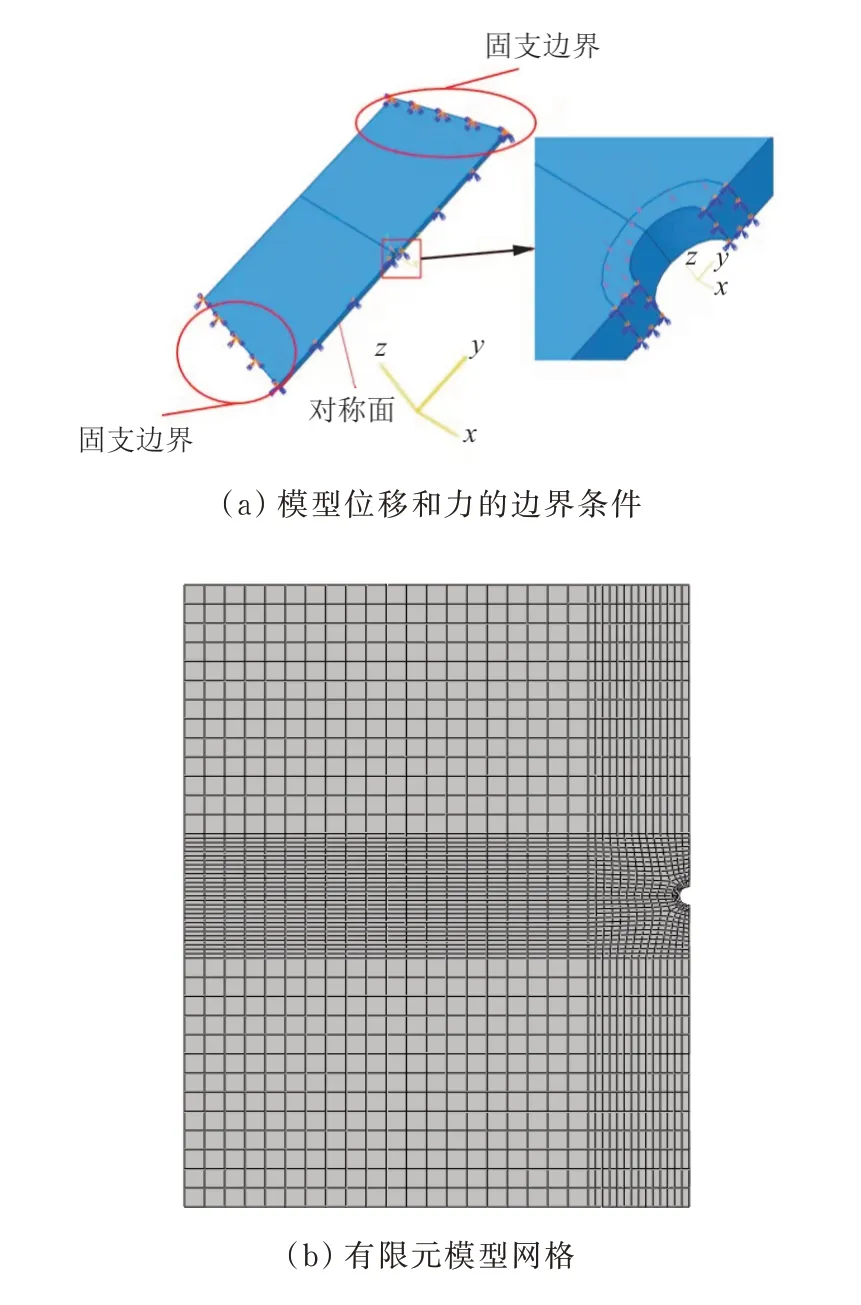
图5 中心带孔板有限元模型Fig.5 Finite element model of plate with a central hole

为了提高计算效率，仅建立1/2模型，并在对称面施加对称边界条件、两端施加固支边界条件。模型中板表面施加合力大小1.8 kN、外径10 mm的环状均匀压强，以模拟薄板受面外法向载荷的情况。模型为线弹性本构，材料为某2系铝合金，弹性模量70 GPa，泊松比0.30，单元类型为八节点六面体线性减缩积分单元C3D8R，网格尺寸在0.04～6.00 mm的范围内。

在FRANC3D中，插入总长2=12 mm的初始直线前缘穿透裂纹，重新划分网格后裂尖附近网格如图6所示（裂尖局部区域网格较细）。裂纹扩展模型中设置应力比=0.1，扩展偏角准则选择最大拉应力准则，裂纹扩展速率公式选用Paris公式d/d=(Δ)，其中，和为材料参数，依 据 试 验 中 的 数 据，为2.136×10，为3.133。

图6 裂尖附近有限元网格Fig.6 Finite element mesh around crack tip

采用FRANC3D-ABAQUS联合方法，计算穿透裂纹的裂纹前缘在受拉面一点不同裂纹长度下的应力强度因子变程Δ，计算结果如图7中黑色线条所示，可以看出：Δ在裂纹长度超过8 mm后，随着受拉面裂纹长度的增加而震荡上升，但上升速度缓慢。计算结果震荡的原因在于，裂纹前缘不断变化的形状，影响了应力强度因子的计算。裂纹扩展速率上升缓慢的原因在于，模拟过程中受拉面裂纹长度大于受压面，导致裂纹前缘与板表面夹角减小，减缓了受拉面应力强度因子的增加。

文献［1］中的试验反推得到的应力强度因子变程如图7中红色点所示，对比模拟结果与试验结果可以看出：受拉面裂纹长度较短时（＜8 mm），FRANC3D计算结果明显大于试验结果，这是因为模拟中初始裂纹在受拉面与受压面的裂纹长度相同，而试验中受拉面裂纹长度远小于此受拉面的裂纹长度，导致试验中受拉面应力强度因子计算值受受压面的影响而降低；受拉面裂纹长度较长时（≥8 mm），应力强度因子变程Δ的计算结果比试验结果稍高（30%～40%），可能是三维裂纹中的裂尖约束效应导致了这一结果。

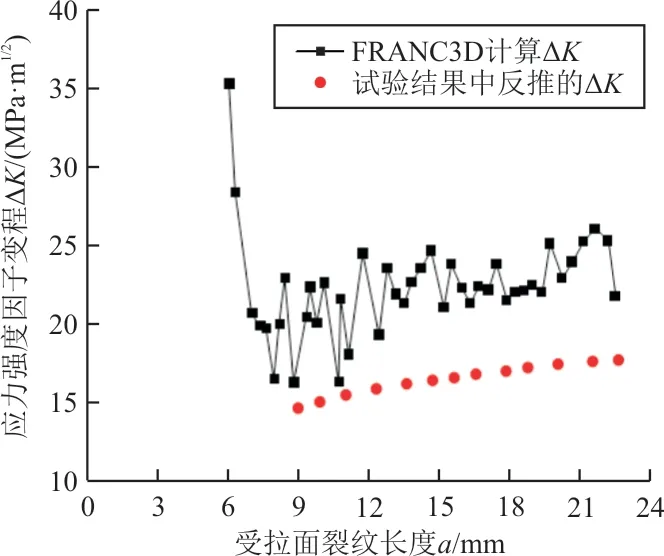
图7 FRANC3D计算和试验［1］反推的受拉面应力强度因子变程Fig.7 Stress intensity factor range on the tension face calculated by FRANC3D and from experiment［1］

总体而言，应力强度因子随裂纹长度变化的计算结果比较符合试验测量的情况，表明FRANC3D-ABAQUS联合方法能够用于面外弯曲载荷下的薄板裂纹扩展的初步分析。

2.3 裂纹前缘形状特点

裂纹前缘形状的数值模拟结果如图8所示，可以看出：裂纹前缘呈1/4椭圆形状，与相关文献中描述的弯曲载荷下裂纹前缘形状相符。然而，本文中，沿厚度方向的裂纹长度达到约3/4板厚时，裂纹向受压面扩展极为缓慢，裂纹在整个模拟过程中未扩展到受压面（受压面裂纹长度为0 mm），这与试验观测的结果不符。在前期的试验研究中，虽然受压面裂纹长度始终小于受拉面裂纹长度，受压面裂纹仍会持续扩展。

图8 裂纹前缘变化Fig.8 Propagation of crack front

在FRANC3D-ABAQUS联合仿真中，无法扩展的部分会阻碍受拉面裂纹的扩展，从而导致受拉面的应力强度因子计算结果偏小。不仅如此，在受拉面裂纹长度达到一定值后，FRANC3D自动划分的网格将发生严重畸变，裂纹扩展模拟将终止。

为了探究上述无法扩展的受压面裂纹对应力强度因子计算结果的影响，本文仍然采用FRANC3D和ABAQUS联合仿真方法和2.2节所述的有限元模型，但不模拟裂纹扩展，而是据试验中测量的受拉面与受压面裂纹长度设置模型中裂纹的长度，并插入1/4椭圆形状裂纹直接计算应力强度因子，并与之前FRANC3D-ABAQUS联合仿真中相同受拉面裂纹长度下的应力强度因子计算结果对比。根据试验结果修正受压面裂纹长度与未修正前的对比结果如表1所示，为试验中受拉面裂纹长度，为试验中受压面裂纹长度，可以看出：FRANC3D-ABAQUS联合仿真的应力强度因子计算结果低于修正长度差后的应力强度因子计算结果，表明受压面裂纹不能扩展这一因素将导致应力强度因子的计算结果偏小10%～15%。

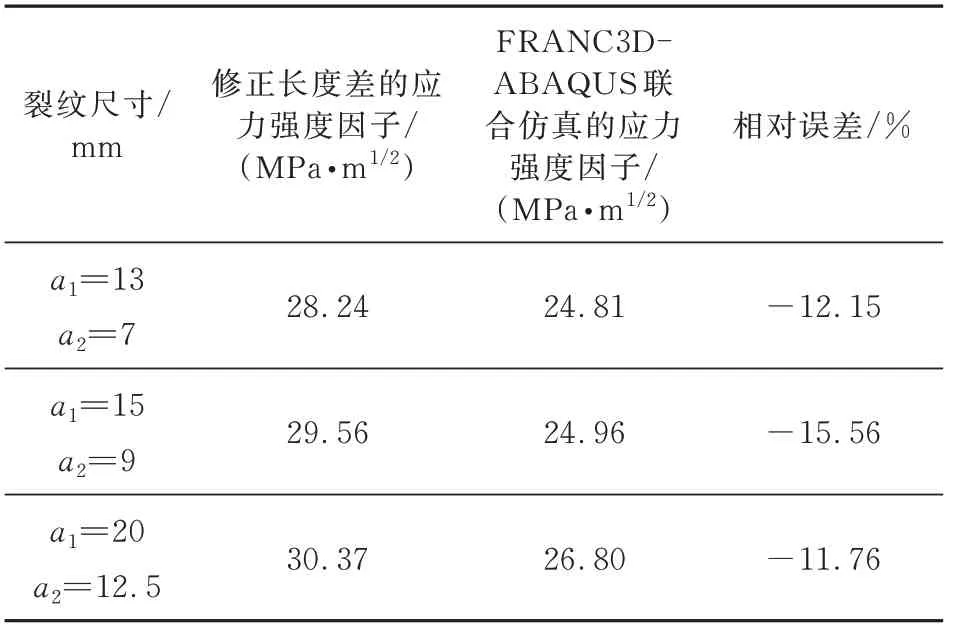
表1 应力强度因子对比Table 1 Stress intensity factor comparison

3 影响疲劳裂纹扩展模拟结果的因素

3.1 边界条件

薄板结构多采用分布式的铆接或螺接形式与其他结构连接。在裂纹扩展分析中，常将这种分布式连接的边界条件简化为简单的边界约束条件。然而，这种边界条件的约束强度，实际上强于铰接却稍弱于完全固支。因此，有必要研究边界约束强度对应力强度因子计算的影响。

计算三种不同边界条件（如图9所示）下的应力强度因子。三种边界条件下的应力强度因子的计算结果如图10所示。

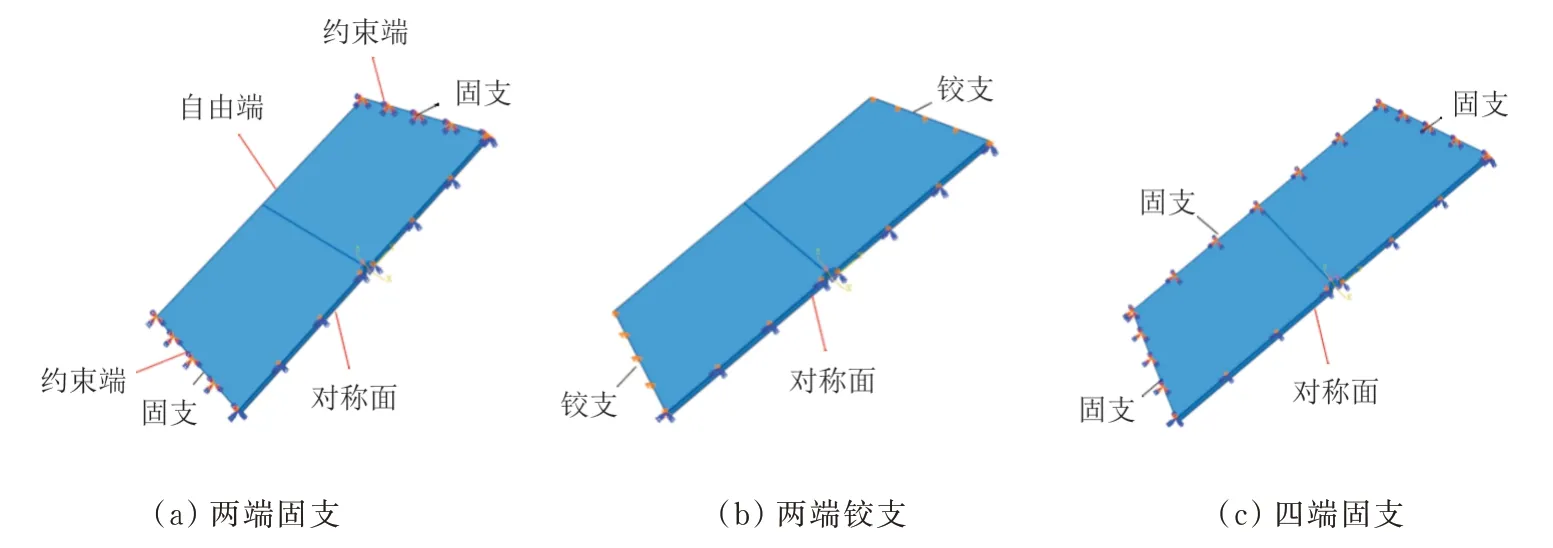
图9 边界条件示意图Fig.9 Schematic images of boundary conditions

图10 不同边界条件下的应力强度因子Fig.10 Stress intensity factor under different boundary

从图10可以看出：两端铰支下的计算结果明显高于两端固支与四端固支，这与弯曲理论计算的两端铰支梁最大应力是两端固支梁最大应力的两倍的结论相符合；四端固支与两端固支下的值几乎相同，表明自由端上的边界条件对的计算结果影响很小，约束端上的边界条件对的计算结果影响较大，并且约束端上的约束越强，计算的值越小。约束端上的边界条件影响明显是因为约束端的边界条件对垂直于裂纹方向上的正应力影响较大，而该方向的应力是裂纹扩展的主要驱动力。

3.2 初始裂纹前缘形状

裂纹萌生的位置和形状，会影响后续的裂纹扩展过程。针对直线前缘穿透裂纹、角裂纹和表面裂纹三种不同初始裂纹形式，通过FRANC3DABAQUS联合仿真，研究初始裂纹前缘形状对裂纹扩展的影响。本文所研究的初始直线前缘穿透裂纹长度为6 mm，角裂纹形状与表面裂纹形状与尺寸如图11所示，分别为半径0.1 mm的四分之一圆与半径0.1 mm的半圆。

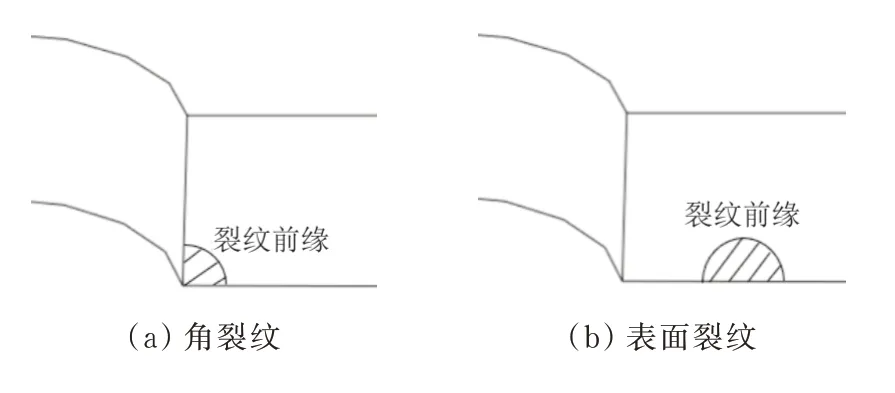
图11 初始裂纹形状Fig.11 Initial crack shapes

裂纹扩展后在受拉面（如图8所示）的应力强度因子计算结果如图12所示，可以看出：初始角裂纹在刚扩展时应力强度因子较小；在裂纹长度约6.5 mm时，初始角裂纹的应力强度因子超过初始直线前缘裂纹；在裂纹长度大于6.5 mm时，初始角裂纹的应力强度因子随裂纹长度的变化规律与初始直线前缘裂纹相似，但数值略高（约20%）。

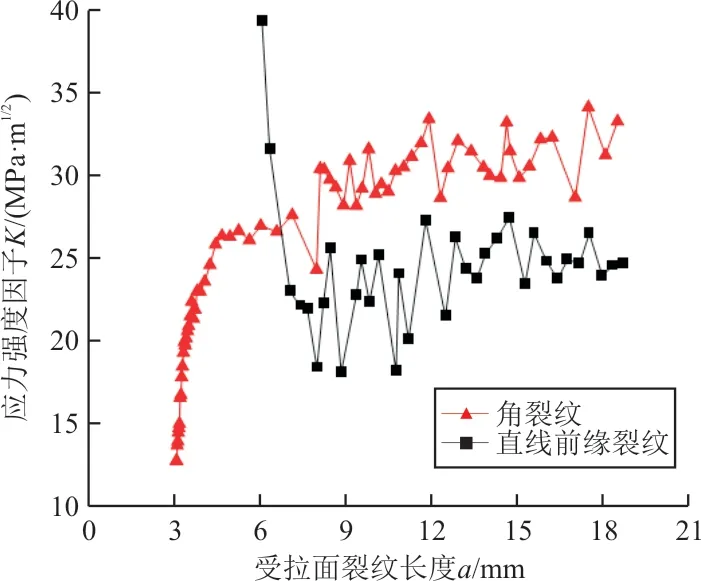
图12 不同初始裂紋的应力强度因子Fig.12 Stress intensity factors under different initial cracks

初始裂纹为角裂纹和表面裂纹的裂纹扩展预测结果如图13所示。由于表面裂纹在扩展一定长度后，就会与圆孔边界面连通，从而产生近似角裂纹的情况，只比较连通前的角裂纹与表面裂纹的裂纹扩展情况（受拉面上的裂纹长度与循环数的关系）。可以看出：角裂纹在裂纹扩展初期的扩展速率较表面裂纹更快。

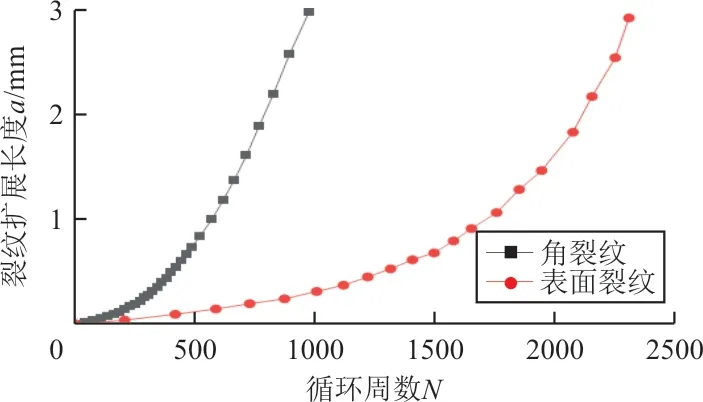
图13 不同初始裂纹下扩展长度与循环次数的关系Fig.13 Relationship between propagation length and cycles under different initial cracks

4 仿真方法的适应性

4.1 FRANC3D计算流程的局限性

FRANC3D裂纹扩展模拟方法无法考虑受压面的裂纹扩展，本文从FRANC3D的计算流程出发，分析该问题出现的原因。

FRANC3D计算流程为：①根据有限元计算结果，计算最大应力强度因子；②根据应力比和计算时设置的其他参数，按照计算流程（如图14所示），计算出Δ；③根据选用的裂纹扩展速率公式，计算一定循环周次后裂纹前缘上每个节点的扩展量。

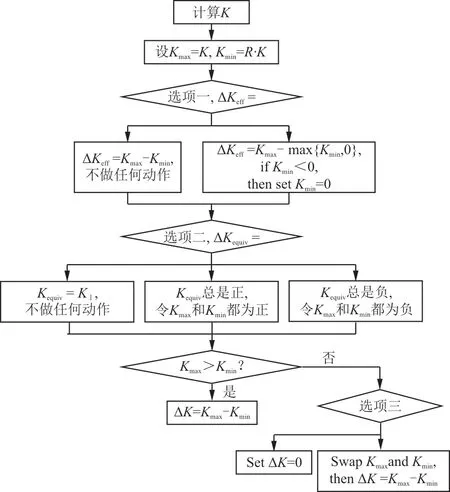
图14 FRANC3D计算ΔK的流程Fig.14 Process ofΔK calculation in FRANC3D

本文模拟的承受弯曲载荷的模型，受压部分的应力始终为压缩应力，故FRANC3D计算的受压部分的应力强度因子近似为0，应力强度因子变程近似为0，基于裂纹扩展公式计算得到的裂纹扩展长度d也近似为0。而裂纹从受拉面向受压面的扩展，主要是靠裂纹前缘扩展的节点“拉动”裂纹前缘的拟合曲线，从而“带动”部分未扩展的节点，如图15所示。而在靠近受压面处，裂纹扩展长度始终接近0，因此扩展的节点也无法“带动”未扩展的节点，导致受压面的裂纹在仿真中始终无法扩展。

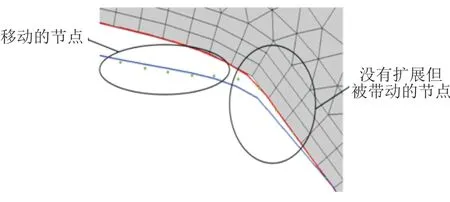
图15 裂纹前缘节点扩展Fig.15 Propagation of nodes on crack front

本文尝试在FRANC3D的框架下，通过调整部分设置，实现受压面上的裂纹扩展。首先，通过调整应力强度因子计算方法，改善受压面上应力强度因子计算结果为0的情况。然而，FRANC3D提供的-积分、虚拟裂纹闭合技术、裂纹张开位移三种计算方法，计算结果相似，无论做出何种选择，受压面的应力强度因子计算结果始终约为0；其次，更改到Δ计算流程中的选项对应力强度因子变程计算结果的影响。然而，任何调整均无法从接近0的得到能使受压面裂纹扩展的Δ；最后，通过调整裂纹扩展速率公式使得裂纹面扩展的尝试也以失败告终，原因在于，基于Δ的裂纹扩展速率公式无法在Δ=0的情况下，计算出裂纹扩展速率。

综上所述，在计算受弯曲载荷下的薄板的裂纹扩展时，由于FRANC3D基于值的计算框架，必将导致总受压缩应力的那一面的裂纹无法在模拟中扩展。

4.2 仿真方法适用的裂纹范围

为了进一步研究FRANC3D方法的适用性，计算面外弯曲载荷下其他类型裂纹的应力强度因子，包括表面裂纹和直线前缘穿透裂纹，这些裂纹也有可能在飞机结构中产生并受面外弯曲载荷作用。

对于两端受弯曲载荷作用下的有限板（=150 mm，=130 mm，=3 mm，如图16所示），采用FRANC3D-ABAQUS联合方法，计算中心表面半椭圆裂纹扩展过程中的应力强度因子的变化，计算结果如表2所示，表2中同时给出应力强度因子拟合公式的计算结果。

图16 有限板中的表面裂纹［5］Fig.16 Surface crack in finite plate［5］

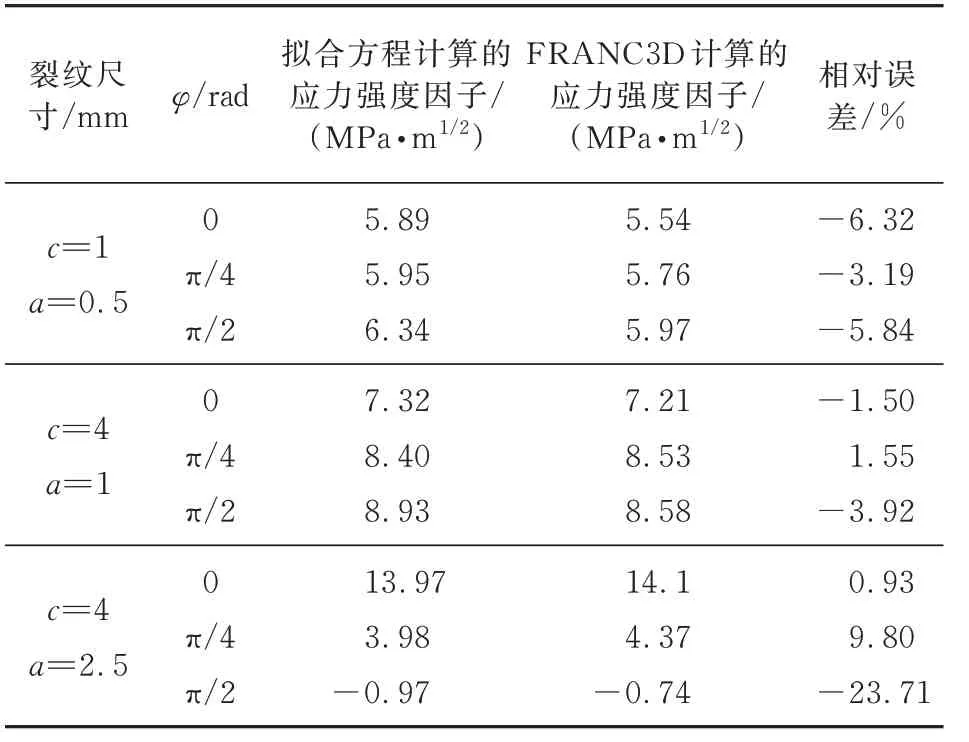
表2 有限板表面裂纹的应力强度因子Table 2 Stress intensity factor of surface crack in finite plate

从表2可以看出：拟合公式的计算结果与FRANC3D-ABAQUS联合方法仅在=2.5 mm、=π/2处，差异较大；其他情况下，差异很小。

对于受弯曲载荷的无限大板（如图17所示），采用FRANC3D-ABAQUS联合方法，计算中心直线穿透裂纹在裂纹扩展过程中应力强度因子的变化，计算结果如表3所示，表3中同时给出文献［3］不考虑裂纹面接触时的理论应力强度因子计算结果。

图17 无限大板中心的直线穿透裂纹［3］Fig.17 Linear penetrating crack in the center of infinite plate［3］

表3 无限大板直线穿透裂纹的应力强度因子Table 3 Stress intensity factor of linear penetrating crack in infinite plate

从表3可以看出：两方法的计算结果在裂纹较短（＜10 mm）时差异较小，在裂纹扩展超过10 mm后，差异较大。

综上所述，针对受弯曲载荷的薄板，FRANC3 D-ABAQUS联合方法能够很好地计算受拉面表面裂纹或穿透裂纹扩展中的应力强度因子，而在分析裂纹前缘形状复杂且板厚度较大的情况时，计算结果不理想。

5 结论

（1）对于面外弯曲载荷下的薄板，在采用FRANC3D-ABAQUS联合方法进行疲劳裂纹分析时，施加较强的边界约束会导致应力强度因子的计算结果增大。

（2）在承受面外弯曲载荷的薄板中，初始非孔边表面裂纹比初始孔边角裂纹在裂纹扩展初期的扩展速率低。

（3）FRANC3D-ABAQUS联合方法在分析面外弯曲载荷作用下薄板孔边裂纹扩展时，存在局限性。现有方法中仅受拉面的裂纹扩展，由于FRANC3D方法对受压面的裂纹应力强度因子变程计算结果近似为0，受压面裂纹无法扩展。