二项式定理题型剖析

胡贵平

(甘肃省白银市第一中学 730900)

二项式定理是高考高频考点，题型多为选择题、填空题，着重考查二项式定理的性质， 主要包括求某项的系数、系数的和差及最值；求某些项、中间项及有理项；利用二项展开式求近似值、求有关整除余数问题及不等式证明；解决与其它数学知识的综合应用．熟悉二项式定理题型就显得非常重要了.

1 求系数

1.1 求某项的系数通项分析法

例1在 (x2+3x+2)5的展开式中x的系数为( ).

A.160 B.240 C.360 D.800

解析由(x2+3x+2)5=(x+1)5(x+2)5，(x+1)5(x+2)5展开式中x的系数为两个因式相乘而得到，

即第一个因式的常数项和一次项分别乘以第二个因式的一次项与常数项，它为

其x的系数为

1.2 求某项的系数的和差赋值法

在解决此类奇数项系数的和、偶数项系数的和的问题中常用赋值法，令其中的字母等于1或-1.

A．1 B．-1 C．0 D．2

解析(a0+a2+a4)2-(a1+a3)2=(a0+a1+a2+a3+a4)(a0-a1+a2-a3+a4) .

实际上，a0+a1+a2+a3+a4和a0-a1+a2-a3+a4分别为已知式在x=1，x=-1的值．

令x=1，得

令x=-1，得

所以(a0+a2+a4)2-(a1+a3)2

=1.

1.3 特殊系数最值对称法

求二项式系数最小的项，需根据各项系数的正、负变化情况，结合二项式系数性质的对称性，与首末两端等距的两项，二项式系数相同求解．

例3在二项式(x-1)11的展开式中，系数最小的项的系数是____.

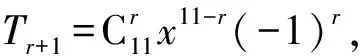
从而可知最小项的系数为

1.4 一般系数最值不等式法

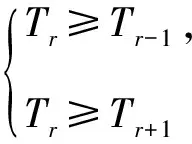
例4(1+2x)n的展开式中第6项与第7项的系数相等，求展开式中二项式系数最大的项和系数最大的项．

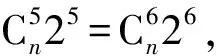
解得n=8．

所以(1+2x)8的展开式中，二项式系数最大的项为

设第r+1项系数最大，则有

解得5≤r≤6．

所以r=5或r=6(r∈{0,1,2,…,8})．

所以系数最大的项为

T6=1792x5，

T7=1792x6．

2 求项

2.1 求中间项

求二项式系数最大的项，根据二项式系数的性质，n为奇数时中间两项的二项式系数最大，n为偶数时中间一项的二项式系数最大.

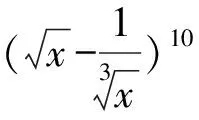
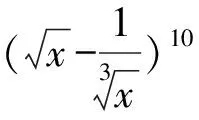
所以展开式的中间项为

2.2 求有理项

当一个代数式各个字母的指数都是整数时，就是有理项．求二项展开式中的有理项，必须合并通项公式中同一字母的指数，令其属于整数，再根据数的整除性求解．

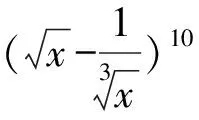
解析因为

所以当r=0,3,6,9时，所对应的项是有理项.

故展开式中有理项有4项．

3 利用展开式

3.1 近似问题截项法

用二项展开式作近似计算，注意底数的变形，以及考查对精确度有影响的某些项．

例7求(2.999)10的近似值(精确到0.001).

解析(2.999)10=(3-0.001)10

=310-10×39×0.001+45×38×0.0012-120×37×0.0013+210×36×0.0014-…

=59049-196.83+0.295245-0.00026244+…

≈58852.465．

所以(2.999)10的近似值为58852.465.

3.2 整除(或余数)问题展开法

用二项式定理解决整除问题，一般将被除式变为有关除式的二项式的形式再展开，经常采用“配凑法”“消去法”结合整除的性质．

例8109192除以100的余数是____．

解析9192=(90+1)92

由此可见，除后两项外均能被100整除．

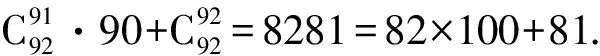
所以109192除以100的余数是81.

3.3 不等式证明二项法

在有二项式的幂不等式中,要善于把其中某个数式变形、分解、引进参数等来构造新二项式而使得不等式两边在二项式展开后有紧密的联系．

例9求证： 3n>2n-1·(n+2)(n∈N，且n≥2)．

证明左式=(2+1)n

注意到：

①2n+n·2n-1=2n-1(2+n)

=2n-1(n+2)；

②n≥2，右式至少三项；

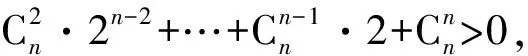
故可以得到3n>2n-1·(n+2)(n∈N，且n≥2)．