一道有关向量求最值问题的探究

王春阳

(江苏省金湖中学 211600)

1 问题呈现、分析与解决

下面给出学生以及我的几种做法.

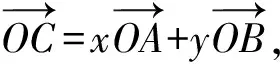
注对于上面的“猜”法并不是所有情况都可以使用.

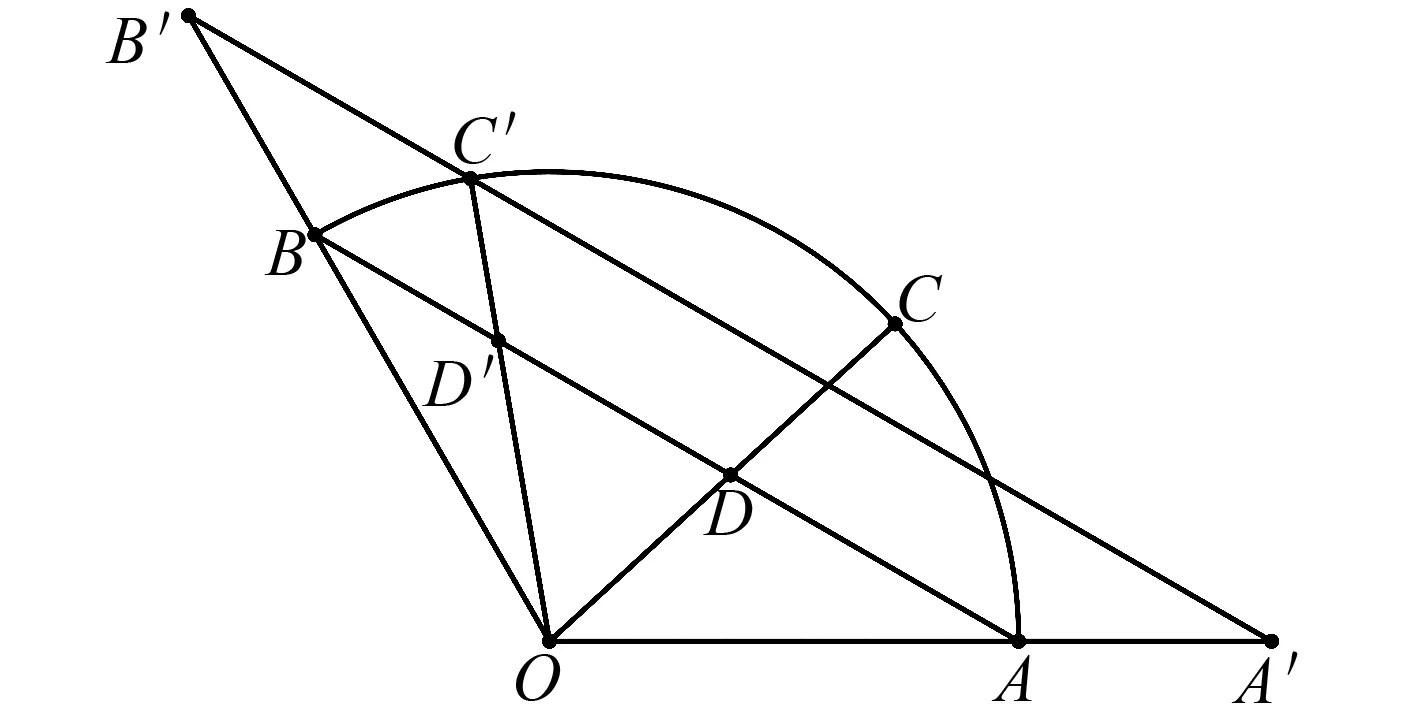
图3

注1从代数角度看，这种方法巧妙地将含有两个变量的式子变成只有一个变量，这要归功于x+y中,x,y前面的系数相同，那如果它们前面的系数不同，其他所给条件不变，此法是否还适用？

注2从几何角度看，只需要找到圆弧上到直线AB距离最远的点即可，同样的，对于x+y中x,y前面的系数不同，其他所给条件不变，是否还是寻找圆弧上距离直线最远的点？

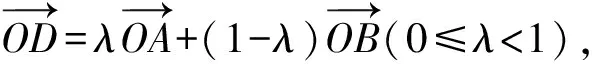
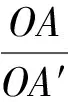
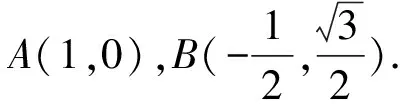
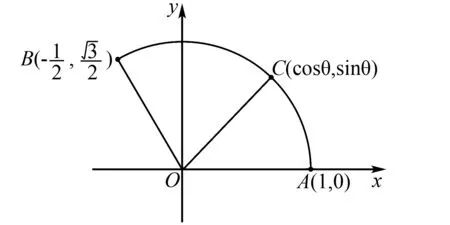
图4

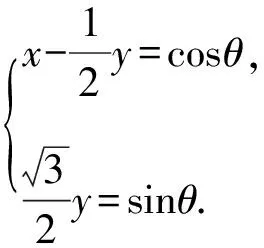
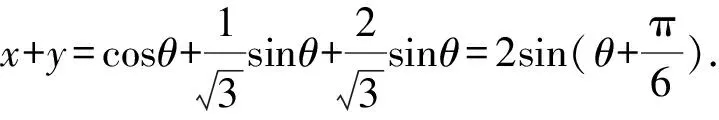
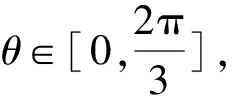
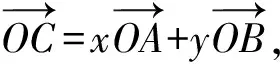
从而(x+y)2=1+3xy.

又1=x2+y2-xy≥xy(当且仅当x=y时取等号),从而(x+y)2=1+3xy≤4.

故x+y的最大值为2，此时x=y=1.

2 问题的延伸

我们对条件中的系数做变化，题目变为：

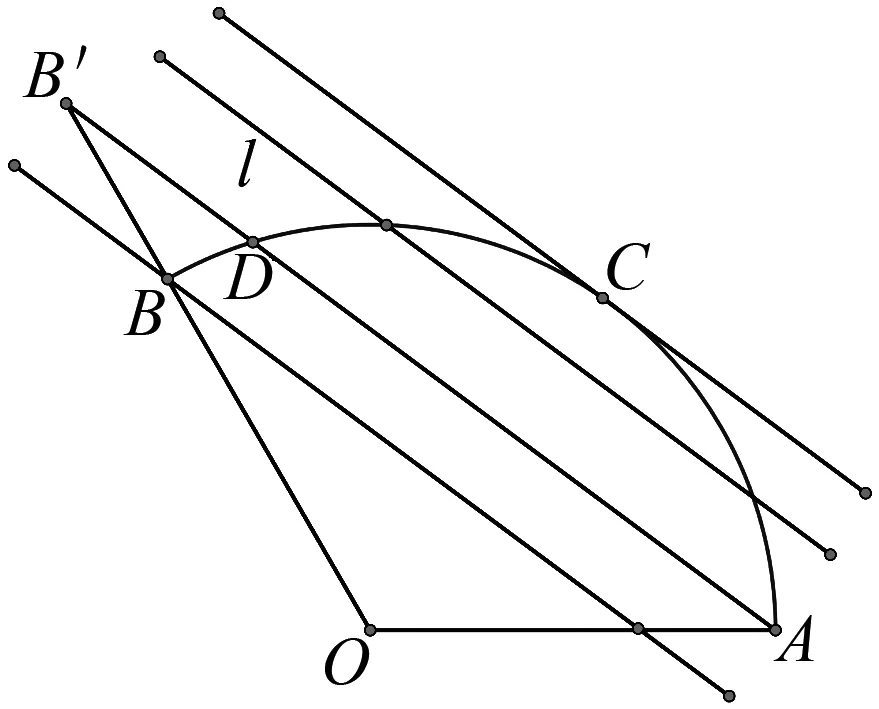
图5

如果我们用猜的方式来看这道题，是不能很明显地猜出来，那么这种方法就有很大的局限性.下面用剩下的几种方法试一下.

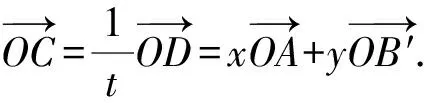
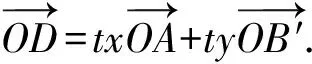
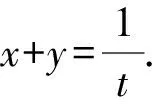
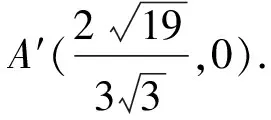
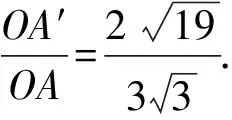
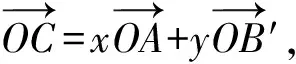
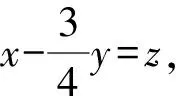
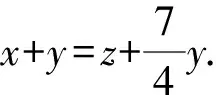
由柯西不等式可得

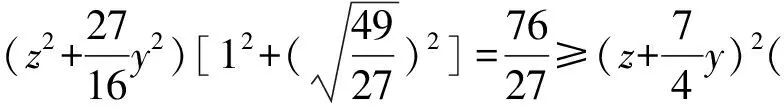
由此例我们可以推广：当改变条件和问题中同一变量前的系数时，问题可以化归到只改变条件或问题的此变量前的系数.那么我们可以类比，如果同时改变条件和问题中两个变量前的参数时，例如：

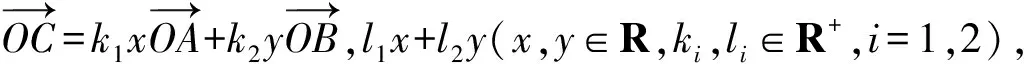
那么如果改变题目中其他我们没有涉及的条件呢？

3 问题本质的探究(数学模型的简化)

在研究了改变条件即前系数几种方法的可行性之后，我们来研究题目本身，从建系的角度去分析题目，如图6,我们将OA,OB隐藏，那么你会发现图中只剩下一段120°的圆弧，以及动点C，定点O，那么我们可以进一步将题目模型简化为：一段函数(两个端点)，函数上一动点，以及函数图象外一点(定点或是动点).我们先从最简单的模型开始，假设认为函数图象外一点为定点，此定点设为二维空间xOy中的原点，即点O，至于这一段函数，我们主要研究高中初等函数，函数的两个端点记为A,B.

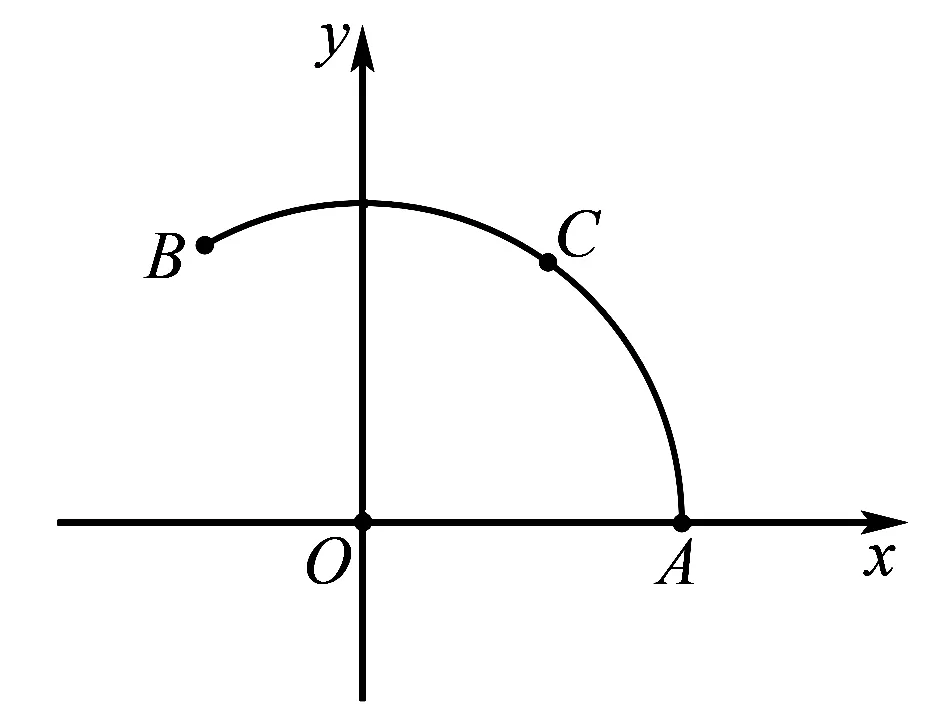
图6

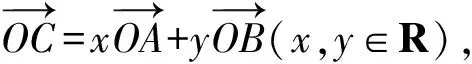
(1)如果函数f(t)是一次函数，且此函数不过原点，那么x+y为定值1.

(3)如果函数f(t)为指数函数，设f(t)=ex，

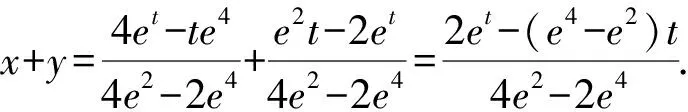
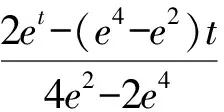
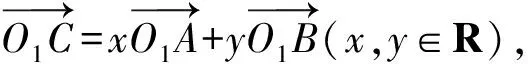
对于数学问题的解决，如同剥洋葱一样，一层层地接近葱芯，慢慢地接近问题的本质，对于上面问题的探讨过程，我们从题目本身引申出很多解决问题的方法，从方法中找到一些方法的局限性和复杂程度，由此引发了我们对问题的延伸，引发我们改变题目中的条件或是问题，会对之前的方法有着怎样影响的思考，从中我们学习到了化归的思想，不仅仅是化归算式，而且还化归了题目.在此基础上，又引发了我们对题目本身的探讨，简化了题目的数学模型，拓广到一般情况，找到了题目的本质，至此我们对整个题目的看法有了质的飞跃.