基于深度迁移学习的多尺度股票预测

程孟菲，高淑萍

西安电子科技大学 数学与统计学院，西安 710126

股票是整个国民经济的重要组成部分，与国家经济发展息息相关。股票的选择和投资策略是股票交易的核心，两者都需要分析未来股票走势。股市每天都会产生大量的数据，对中小投资者来说，很难从大量的数据中分析股票的未来趋势并进行决策。

股票数据具有非线性、不稳定的特征，数据量大，同时具有很高的噪声[1]。股票价格的变动受到经济、政策、市场和投资者心理等多重因素的影响，增加了股票预测的难度。随机游走假设的提出，为能否利用历史信息预测信息提出挑战[2]。随机游走假设认为，市场上股票的价格已经反映了所有的信息，所以余下的价格波动都是源于无法预测和捕捉的随机事件，因此股票的价格波动是一种随机游走的形态。随着技术的进步，对股票预测问题的研究有了很大的发展。很多学者通过对非线性、不稳定的股票数据进行平稳化或降噪处理，预测股票未来走势，如娄磊等人[3]利用小波对股票进行降噪，贺毅岳等人[4]通过分解对数据进行平稳化处理。

股票价格预测模型可分为传统模型、机器学习模型、深度学习模型。传统回归模型如多项式回归、线性回归、差分移动自回归模型（autoregressive integrated moving average，ARIMA）[5]等，但是难以捕获股票历史数据和未来价格之间的关系，预测误差大。机器学习模型可以捕获人难以发现的内在关系，股票预测常用的机器学习模型有支持向量机[6]、随机森林[7]、K邻近值[8]等。深度学习是机器学习的进一步发展，常见的深度学习模型有卷积神经网络（convolutional neural networks，CNN）、循环神经网络（recurrent neural network，RNN）、长短期记忆网络（long short term memory network，LSTM）。其中由于LSTM解决了模型训练过程中RNN的梯度消失以及梯度爆炸的缺陷，被广泛用于股票预测问题的研究中[9-10]。Zhao等人[11]重新定义股票趋势预测的时间权重LSTM模型，Mootha等人[12]使用双向LSTM对印度股票进行预测，Althelaya等人[13]采用双向LSTM和堆叠LSTM对股票进行预测，Qian等人[14]在引入静态分析，验证LSTM的预测效果与数据的非平稳性之间的关系。Li等人[15]提出自适应的梯度下降算法训练CNN-LSTM模型，预测效果优于传统的梯度下降算法。Nguyen等人[16]提出DTRSI模型，利用深度迁移学习训练LSTM网络，有效提高了股票的预测效果。经验模态分解（empirical mode decomposition，EMD）将时间序列数据分解为一组与不同时间尺度相关的分量和趋势，即本征模函数（intrinsic mode function，IMF）和残差（residual，RES），其中IMF反映了在不同时间尺度下数据的震荡情况，RES则反映了市场趋势。张倩玉等人[17]利用EMD提出EMD-LSTM模型，表明EMD能有效提高不稳定、高噪声数据的预测效果。

虽然基于深度学习的模型提高了股票的预测效果，但是现有的股票预测方法主要利用了股票的历史数据而忽略了来自其他股票的有效信息，股票价格的涨跌受到其他股票的影响，某一支或多支股票价格的涨跌会影响相关行业内其他股票价格的变化[18]。为了进一步提高股票预测效果，本文提出了一种多尺度股票价格预测模型TL-EMD-LSTM-MA（TELM），预测股票的收盘价。TELM首先通过EMD将收盘价分解多个尺度分量，即多个IMF和RES；然后，将多个IMF和RES分为高频部分和低频部分，针对高频部分，采用基于深度迁移学习的方法进行预测，即先利用市场内其他股票数据训练预训练模型，再利用待预测股票或指数的对应分量对模型进行微调和预测，针对低频部分采用移动平均法（moving average，MA）预测；最后，将所有分量的预测值相加作为最终的预测输出。为了验证TELM的性能，分别对单支股票和上证指数、深证成指、上证50、中证500、沪深300进行预测。其中单支股票包括中国A股市场20个行业的500支股票，并分别从行业、上市时间等因素对实验结果进行分析。实验结果表明TELM在单支股票和指数的预测上比MA、LSTM、CNN-LSTM、EMD-LSTM、DTRSI效果更好，降低了模型的训练规模，节约了时间成本，有较好的泛化能力。进一步通过模拟股票的交易过程，表明TELM预测的股票收盘价对股民的投资决策有重要的参考价值，提高了投资回报率，降低了损失。

1 相关理论知识

1.1 经验模态分解

任何非线性、非平稳的信号都可以通过经验模态分解[19]（EMD）将原始信号分解为多个本征模函数（IMF）和残差（RES）。EMD在处理数据的过程中，不需要设定基函数，根据数据自身的尺度特征进行分解。IMF必须满足两个条件：

（1）在时间范围内，局部极值点和过零点的数目必须相等或相差1。

（2）在任意时刻，局部最大值的上包络线和局部最小值得下包络线均值必须为0。

假设原始信号为S(t)，EMD的分解过程如下：

步骤1确定原始序列S(t)的所有极大值和极小值。

步骤2采用3次样条插值法，根据极大值与极小值构造S(t)的上下包络线。

步骤3由上下包络线计算出S(t)的局部均值m1t(t)，以及差值S(t)与的m1i(t)差值：

步骤4用h1i(t)代替原始序列S(t)，重复步骤1～3，直到h1i(t)和h1i-1(t)的差值小于阈值，则第一个IMF分量即为h1i(t),记作IMF1(t)=h1i(t),r1(t)=S(t)-IMF1(t)，S(t)=r1(t)。

步骤5重复步骤1～4，直到rn(t)不能再分解出IMF分量。其中S(t)的分解结果如下表示：

这里RES=rn(t)为趋势项，i越小，IMFi(t)单位时间内震荡幅度越大。

1.2 深度迁移学习

迁移学习把知识从一个或多个领域（源域）迁移到另一个领域（目标域），利用已知某领域的知识求解不同但相关领域的问题[20-21]。已经在图像分类[22]、自然语言处理[23]等领域有很多应用，受到越来越多的关注。与机器学习、深度学习相比，迁移学习不再假设训练数据和测试数据必须是独立同分布，因此目标模型的训练不需要从头开始训练，降低了对训练数据的要求，加快训练速度。Tan等人[24]给出了迁移学习和深度迁移学习的定义。

定义1（迁移学习）。给定一个基于数据Dt的学习任务Tt，以及基于数据Ds的学习任务Ts。发现Ds和Ts中的隐知识，并用来提高任务Tt的函数FT(⋅)效果的任务，称为迁移学习。其中Dt≠Ds，Tt≠Ts，且Ds的数据量远大于Dt。

定义2（深度迁移学习）。给定一个＜Ds,Ts,Dt,Tt,FT(⋅)＞的迁移学习任务，如果FT(⋅)是基于深度学习的非线性函数，则称该任务为深度迁移学习。

1.3 长短期记忆网络

为了解决RNN在训练过程中梯度消失和梯度爆炸的问题，Hochreiter等人[25]提出了LSTM模型，解决了传统神经网络长期和短期依赖的问题。LSTM模型使用长短期记忆细胞记录长短期信息，其结构单元如图1所示，可以概括为三门两态：输入门it、输出门ot和遗忘门ft，以及单元状态ct和隐藏状态ht。

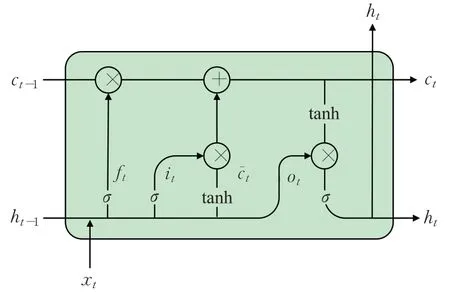
图1 LSTM结构图Fig.1 Structure of LSTM

输入门：用于记忆当前输入数据的信息，包括sigmoid层和tanh层。sigmoid层决定哪些信息将被更新，tanh层用于创建新的变量c͂t。

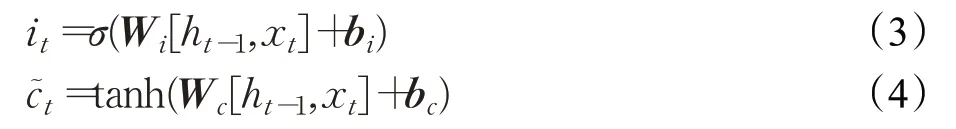
遗忘门：用于选择过去的哪些信息将被遗忘，1表示完全保留历史信息，0表示完全遗忘历史信息。

其中，[ht-1,xt]表示将ht-1和xt进行拼接，⊙表示矩阵的哈达玛积，Wf、Wi、Wc、Wo为权重矩阵，bf、bi、bc、bo为偏置，权重矩阵和偏置将在模型的训练过程中不断优化。

1.4 移动平均方法

Joseph E.Granbville提出均线理论，杜云峰[26]验证了利用均线对股市趋势进行判断，能提高投资者收益。均线是由移动平均法（MA）计算前N个数据的平均值。对一维向量x，预测向量y的计算公式如下：

2 TELM股票预测模型

本文通过EMD对股票收盘价进行的多尺度分解，并利用深度迁移学习、堆叠LSTM模型以及移动平均法，加入模型选择机制，构建多尺度股票预测模型TELM，模型流程如图2所示。针对待预测的股票或指数，首先将收盘价经过EMD分解，获得In个不同尺度的IMF和RES，并根据In的大小将其划分为高频部分和低频部分，高频部分包括h个分量IMF1,IMF2,…,IMFh，低频部分包括In-h+1个分量IMFh+1,…,IMFIn,R ES，h取值为：

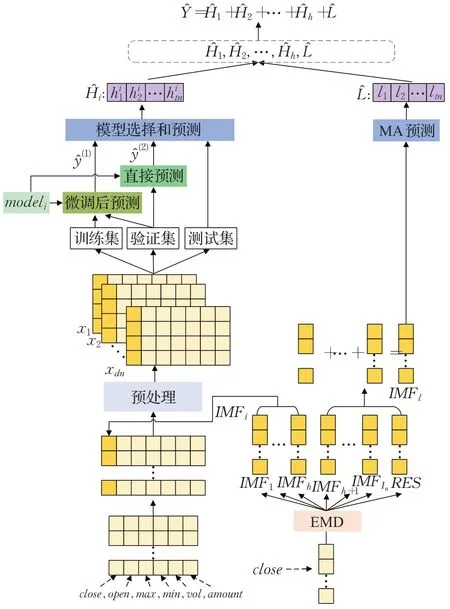
图2 TELM模型流程图Fig.2 TELM model flow chart

TELM模型分两步，分别进行预训练模型的训练和单支股票或指数的模型训练与预测，步骤如下：

步骤1预训练模型的训练。预训练数据集的50支股票，每支股票的IMF的个数In≥7，即高频部分的分量包括IMF1,IMF2,…,IMF5，分别训练对应的预训练模型model1,model2,…,model5。针对IMFi,i=1,2,…,5,训练堆叠双层LSTM的深度学习模型modeli，该模型结构如图3所示，输入的数据包括预处理后的第j至第j+time_step-1天的IMFi、开盘价（open）、收盘价（close）、最高价（max）、最低价（min）、成交量（vol）和成交额（amount），输出数据ŷj为IMFi在第j+time_step天的预测值，time_step为时间步长。

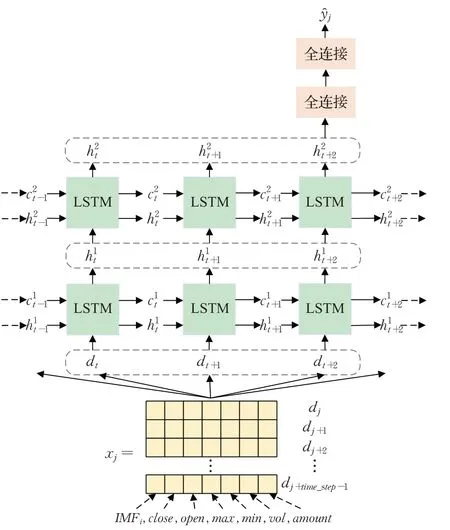
图3 堆叠LSTM流程图Fig.3 Two-layer LSTM model flow chart

步骤2单支股票或指数的预测。对高频部分和低频部分采用不同的方法进行预测，并将所有分量预测值相加。

步骤2.1高频部分的预测。针对IMFi,i=1,2,…,h,输入数据通过预处理后，将其划分为训练集、验证集和测试集。利用训练集微调modeli部分参数，并对验证集进行预测，得到预测值ŷ(1)；利用modeli直接对验证集进行预测，得到验证集的预测值ŷ(2)；通过分别比较ŷ(1)、ŷ(2)并与测值真实值的误差进行模型选择，判断modeli微调后预测误差是否变小，如果ŷ(1)与真实值的误差更小，则利用微调后的模型对测试集进行预测，否则直接使用预训练模型modeli进行测试集的预测。最终得到IMF1,IMF2,…,IMFh的测试集预测值Ĥ1,Ĥ2,…,Ĥh。

步骤2.2低频部分的预测。计算分量和IMFl，计算公式如下：

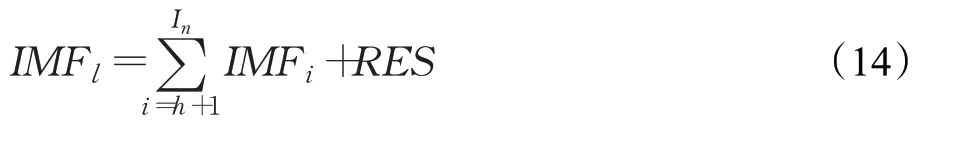
并利用移动平均法计算测试集的预测值L̂，即

步骤2.3最后将Ĥ1,Ĥ2,…,Ĥh和L̂的预测值进行相加，结果作为最终的股票预测值Ŷ，计算公式如下：

3 实验结果及分析

分别对数据及模型参数、单支股票预测结果、指数预测结果、股票交易模拟进行分析。数据及模型参数是对数据和参数设置进行说明；单支股票预测结果分析除了比较不同模型的性能外，还从行业、IMF个数、上市时间等方面分析预测误差；指数预测结果分析旨在验证TELM是否能降低指数预测的误差，提高预测效果；股票交易模拟则是基于股票的预测收盘价模拟股票交易过程，验证TELM在股市交易中是否能降低投资风险、提高投资回报率。

3.1 数据及模型参数

3.1.1 数据来源

实验所用股票数据来自财经数据接口包Tushare（https：//www.tushare.pro），包含20个行业的550支股票以及上证指数、深证成指、上证50、中证500、沪深300从2010年11月1日至2021年11月1日的历史行情信息。预训练数据集包括来自酿酒、新能源车、有色金属、环保工程4个行业共50支股票数据，用于步骤1中预训练模型，每支股票的上市时间都在5个月以上；预测数据集包括500支股票和上证指数、深证成指、上证50、中证500、沪深300，单支股票或指数的数据被划分为训练集、验证集、测试集，分别占总数据的80%、10%、10%，用于步骤2中模型的训练、选择和预测，并验证模型的性能。

3.1.2 数据预处理

为了消除不同特征数据量纲的影响，在训练前，对数据进行Min-Max归一化，对归一化后的数据根据时间步长time_step切分数据。

Min-Max归一化的计算公式如下：

其中，xi为需要归一化的数据，yi为归一化后的数据，ŷj为预测数据，x͂j为反归一化后的数据。

3.1.3 性能指标

采用均方根误差（root mean squared error，RMSE）、平均绝对误差（mean absolute error，MAE）和决定系数R2评估模型的性能，其中R2评价回归模型系数拟合优度，R2越高，表示可以被解释的程度越高，回归模型的效果越好。评价指标的计算公式如下：

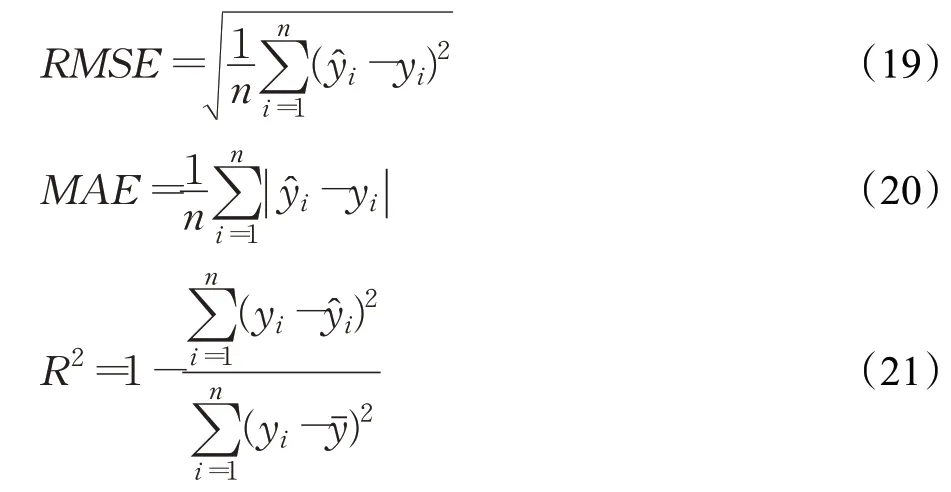
ŷi,yi分别代表预测值和真实值，yˉ表示yi的均值。

3.1.4 参数设置

在TELM的训练和预测过程中涉及许多超参数，超参数的设置影响着最终的预测效果，超参数设置如表1至表3所示。

表1 堆叠LSTM模型的参数Table 1 Parameters of the stacked LSTM Network

通过网格搜索算法[27]，寻找最优的双层LSTM模型的参数，参数设置如表1所示，其中out_dim表示该层的输出参数，activati on表示该层的激活函数，batch_size表示每轮训练的样本个数，time_step表示时间步长，optimizer表示模型训练使用的优化器，损失函数为MSE。

在步骤2.1预测过程中涉及到模型的微调，微调模型哪些层的参数对模型的训练效果以及模型的训练的时间成本有很大的影响，为了确定最优的微调参数，分别选择不同层的参数进行对比实验，实验结果如表2所示。从表2中可以看出微调第4、5层的参数要优于微调其他层参数，在降低预测误差的同时，训练参数由12 201降至321，减少了97.4%。因此在步骤2.1预测高频部分的分量时，将第4、5层的参数设为可微调的层。

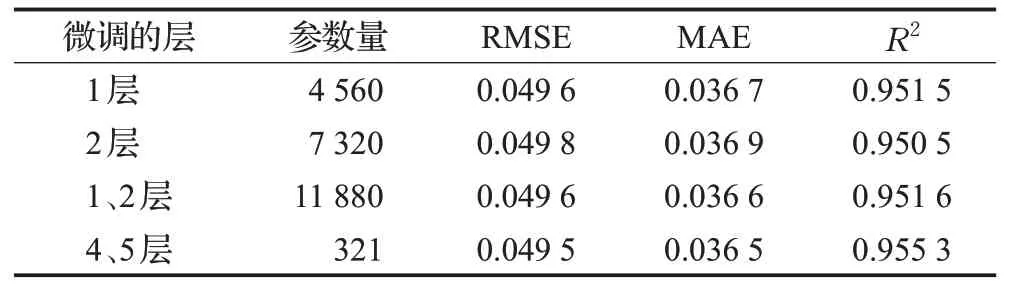
表2 微调的层及其性能指标Table 2 Fine-tuning layers and their performance indicators

TELM模型涉及到高频部分包含的分量数量h,h的最大值设为5，h越大表明预训练模型的数量越多，训练时间越长。由于股票上市时间不同，以及每支股票数据的复杂程度不同，导致某些股票经过EMD分解后得到的IMF分量个数不同，因此必须确定h的最大值。h取不同值时的预测性能如表3所示，h越大，预测误差越低，预测结果越好，在h=5时，预测误差最低，且拟合度最好。在预测数据集中94%的股票的IMF分量个数In大于等于5。

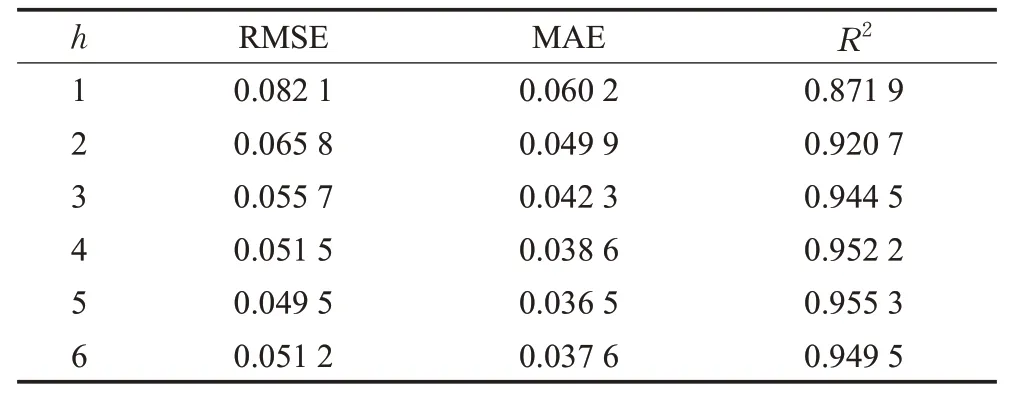
表3 取值及其性能指标Table 3 Performance indicators of different value of h

3.2 单支股票预测结果分析

3.2.1 不同模型的性能比较

为了验证TELM的性能，对预测数据集的500支股票通过不同的模型进行预测，包括MA、LSTM、CNNLSTM、EMD-LSTM以及迁移学习模型DTRSI进行对比，不同模型的性能指标如表4。从表4中可以看出EMDLSTM、DTRSI以及TELM的预测结果显示，RMSE和MAE误差低于LSTM和CNN-LSTM，R2数值也远高于LSTM和CNN-LSTM，EMD-LSTM和TELM对股票数据进行了多尺度分解，说明多尺度分解能有效降低股票的预测误差，而DTRSI和TELM的预测效果则说明迁移学习同样提高股票预测的拟合效果。表4中股票个数一项可以看出，在500支股票中，TELM在428支股票的预测任务中表现最优，占总量的85%，说明TELM的泛化能力强，在股票的批量预测任务中具有优势。

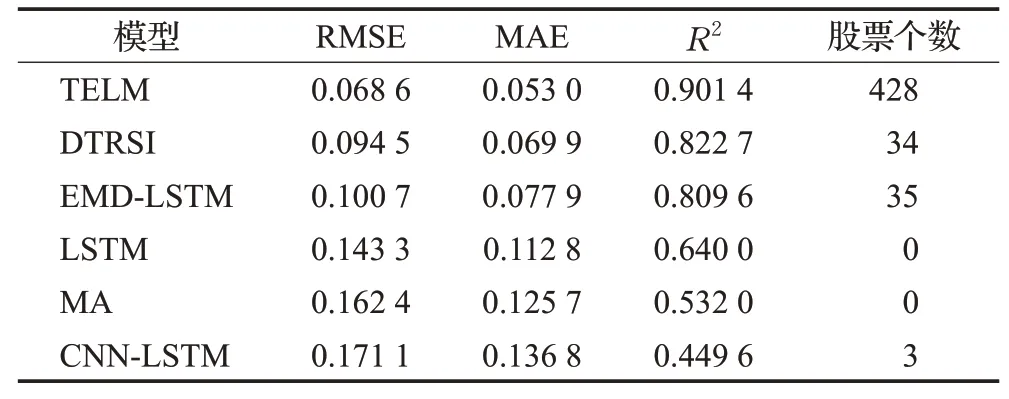
表4 六种模型的预测性能指标Table 4 Performance indicators of six models

图4、图5、图6分别为三元股份、圣龙股份、西王食品3支股票2021年6月17日至2021年11月1日的预测曲线图，从曲线中可以看出，图4总体呈现上涨趋势，图5股票总体先涨后跌，图6总体呈下跌趋势，从图4至图6可以看出TELM模型不仅能捕获股票未来趋势，而且在股票的总体走势变化较大的拐点预测准确，如图4中8月20、10月8日。提前预测出股票趋势变化幅度较大的点，为投资者的投资决策提出重要的依据，能有效提高股民的收益和降低投资风险。

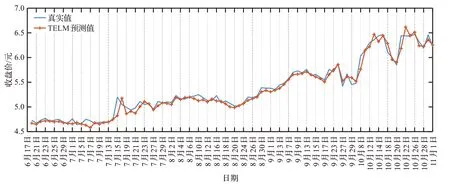
图4 三元股份收盘价预测曲线Fig.4 Sanyuan shares closing price forecast curve

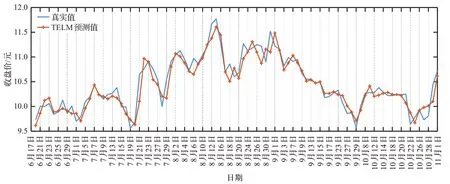
图5 圣龙股份收盘价预测曲线Fig.5 Shenglong shares closing price forecast curve

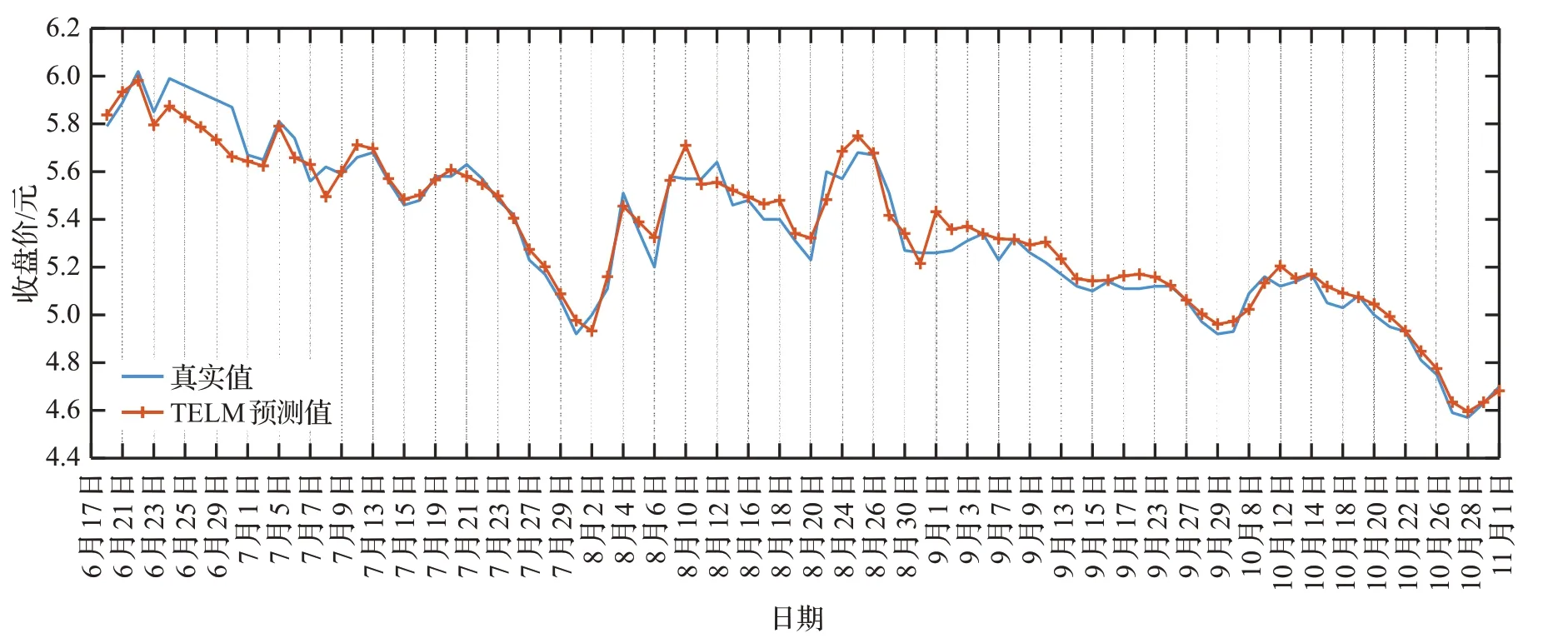
图6 西王食品收盘价预测曲线Fig.6 Xiwang foods closing price forecast curve

3.2.2 行业因素、上市时间、IMF数量分析

由于在源模型数据集包括酿酒、新能源车、有色金属、环保工程4个行业的股票数据，为了比较TELM的预测效果是否受行业因素的影响，本小节对多个行业的预测性能指标进行对比，不同行业性能指标如表5所示。在源模型数据集包含的4个行业中，环保工程行业的预测效果最差，该行业的股票的预测性能指标的均值分别为0.060 7、0.044 8、0.932 7。在源模型数据集不包含的行业中，除房地产和航运港口外，行业5至行业11的性能指标均比环保工程的性能指标差。因此，源模型数据集中是否包含该行业，对该行业的股票预测会有一定的影响。通过在源模型数据集中加入某行业的股票，能提高该行业内其他股票的预测效果。

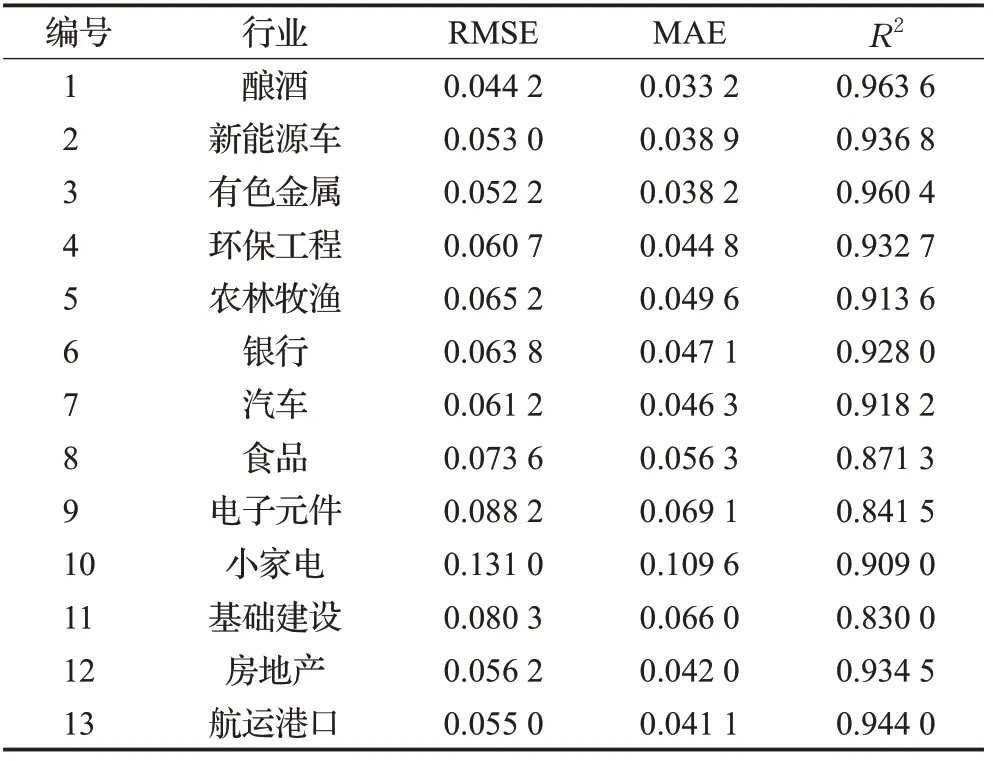
表5 不同行业的性能指标Table 5 Performance indicators of different industrys

由于上市时间不同，数据集的股票的数据量不同，为了分析股票的预测效果与股票数据量的关系，根据股票的数量大小划分为不同的区间，该区间内股票的预测误差和拟合优度的平均值如表6。从结果可以看出，当股票的数据量大于500，RMSE、MAE及R2变化不大；当股票的数据量小于500时，性能指标较差。每年的交易日约为250天，所以上市两年以上的股票，比上市不足两年的股票的预测误差小、拟合优度高，预测效果更好。

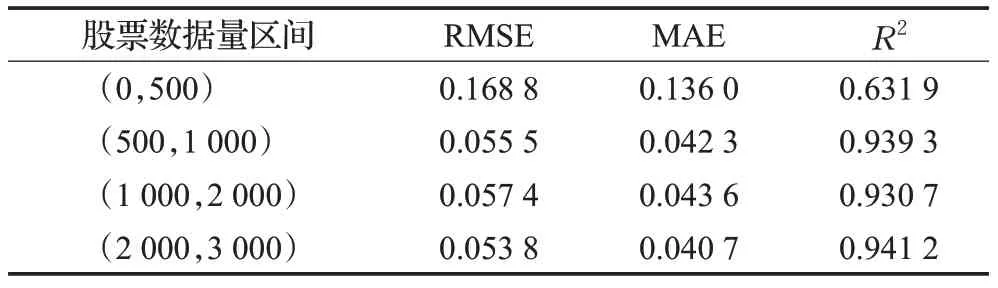
表6 不同股票数据量区间的性能指标Table 6 Performance indicators of different intervals of stock data volume

利用EMD将股票数据分解为不同尺度分量，由于数据的复杂性不同，分解后的IMF数量不同，计算IMF数量为i的所有股票的RMSE、MAE及R2均值，i=1,2,…,10，图7中（a）、（b）分别为RMSE、MAE及R2随IMF数量变化曲线图。从图中可以看出，当IMF数量大于等于6时，误差降低的速度和R2增长速度变缓，说明当股票的IMF数量大于等于6时，IMF分量数目对股票预测误差的影响较小，而IMF分量数量小于6时，股票的预测误差相对较高。因此EMD分解后IMF分量数目大于等于6的股票预测效果更好。

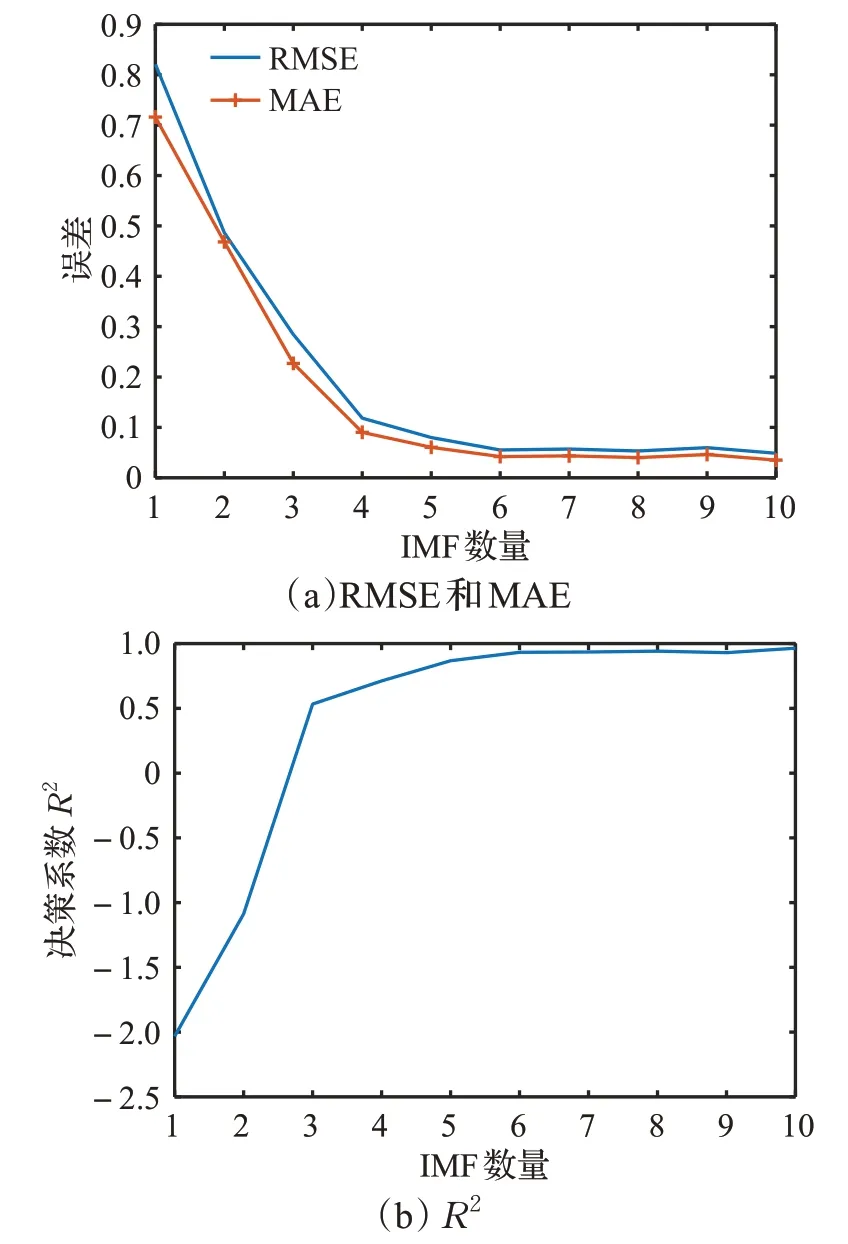
图7 RMSE、MAE、R2随IMF数量变化曲线图Fig.7 Change curve with IMF of RMSE、MAE、R2

3.3 指数预测结果分析

股票指数反映了股票市场的价格涨跌，投资者通过股票指数的变动情况预测股票市场未来的走势。本节对上证指数、深证成指、上证50、中证500、沪深300通过不同的模型对其进行预测，预测结果见表7至表11。从表中可以看出，TELM的预测效果最佳，其次是EMDLSTM模型。其中TELM模型在上证50的预测中，R2值比EMD-LSTM提高了5.6%，说明TELM能有效提高股票指数的预测效果，更好地捕捉市场未来走势。

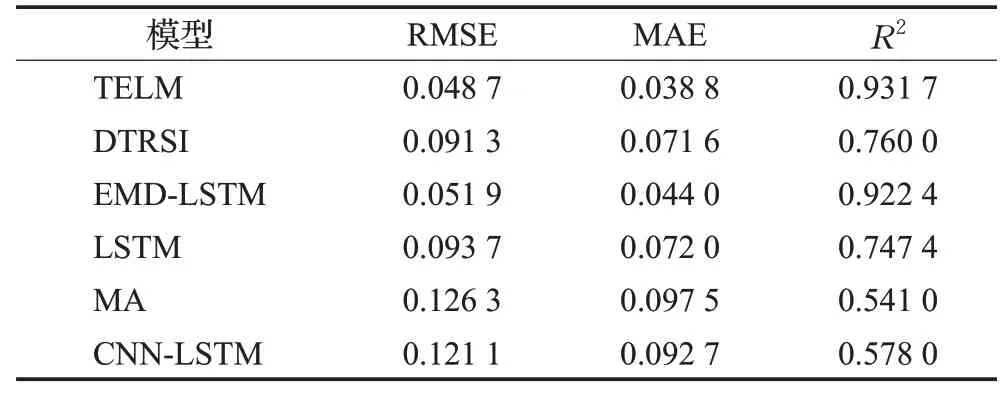
表7 上证指数的预测性能对比Table 7 Comparison of prediction performance of Shanghai stock index

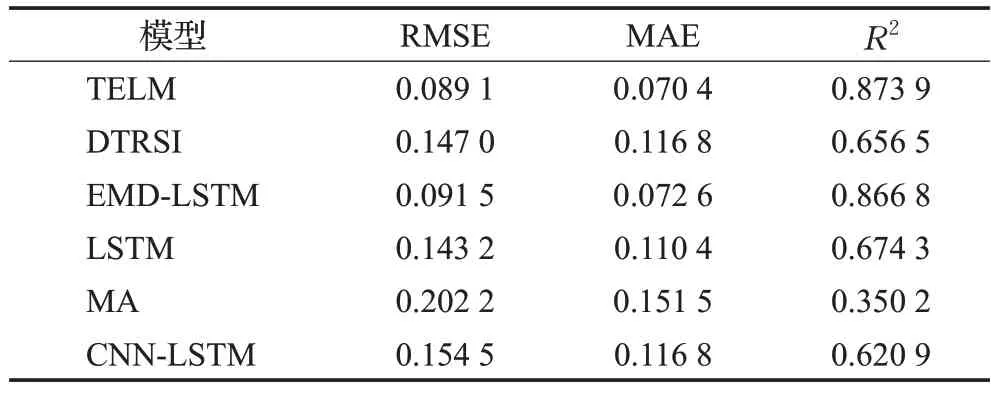
表8 深证成指的预测性能对比Table 8 Comparison of prediction performance of SZSE com-ponent index

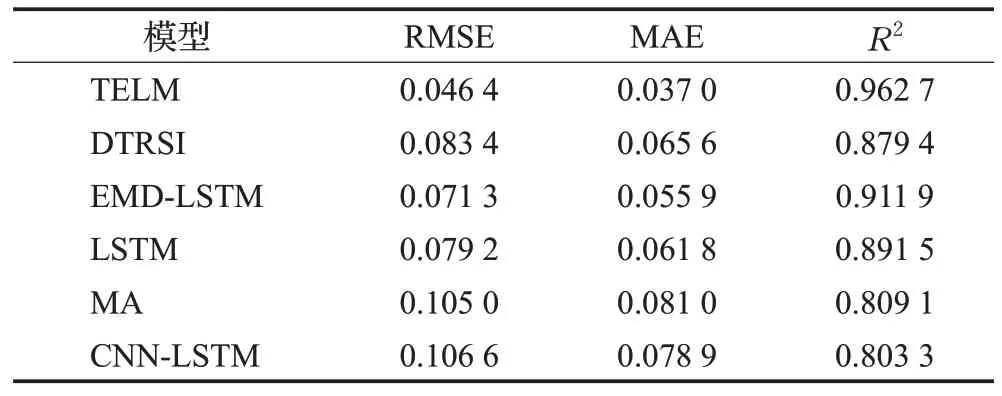
表9 上证50的预测性能对比Table 9 Comparison of prediction performance of SSE 50

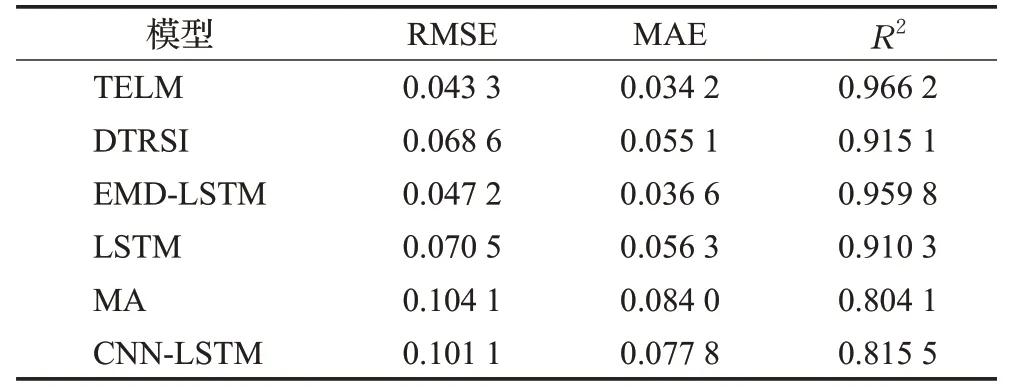
表10 中证500的预测性能对比Table 10 Comparison of prediction performance of CSI 500

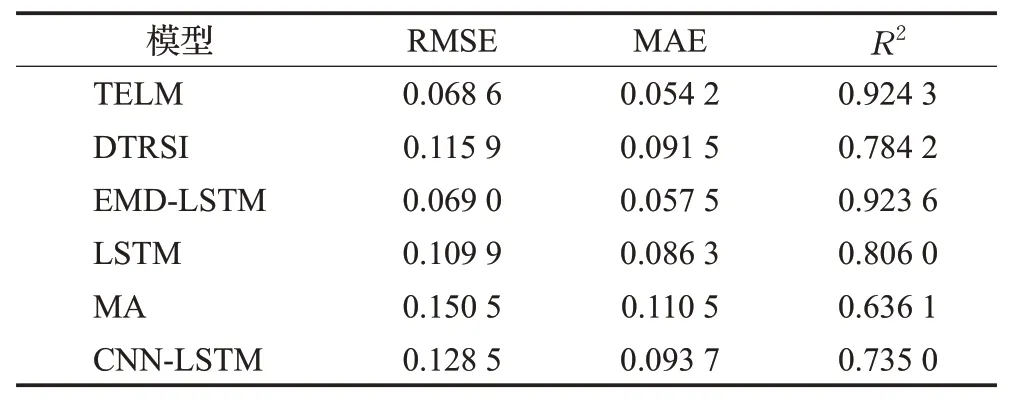
表11 沪深300的预测性能对比Table 11 Comparison of prediction performance of CSI 300

3.4 股票交易模拟

当选择一支股票进行投资时，由于无法准确估计股票未来很长一段时间的涨跌情况，难以确定股票的买入和卖出的时机。投资中收益越高意味着风险越高，如何在一定风险下获得最大收益是很多投资者关心的问题。本节模拟真实的股票交易过程，利用股票的预测收盘价，计算预测回报率，提出一种股票投资策略，获取在这种策略下股票的损失与收益情况。回报率反映了股票的盈利能力，当回报率大于0时，回报率越高说明收益越高，当回报率小于0时，回报率越高说明损失越小。T时的回报率RT以及预测回报率RPT的计算公式如下：

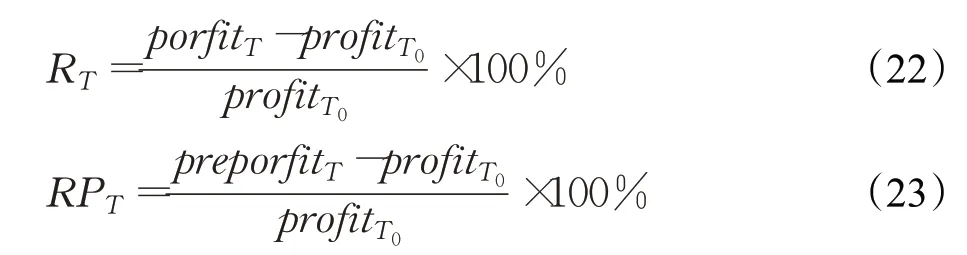
其中，porfitT表示T时的资产总值，profitT0表示初始时刻T0的资产总值，preporfitT表示根据T时预测收盘价ŶT计算的买入或卖出后的资产总值。

假设初始时刻T0时资产总值profitT0为10 000元，每次买入都是用目前的总资产全部买入该股票，每次卖出都是将持有的股票全部卖出，并考虑每次买入和卖出的交易手续费为0.4%。根据预测回报率RPT、预测收盘价ŶT以及T-1、T-2时的真实收盘价YT-1、YT-2，基于“低价买入、高价卖出”的原则，制定的投资策略如下：当未持有该股票时，如果T-1时的收盘价YT-1低于T-2时的收盘价YT-2、T时预测收盘价ŶT比T-1时降低0.5%，即YT-1＜YT-2、ŶT＜YT-1×(1-0.5%)，则全部买入；当持有股票时，如果T-1时的收盘价YT-1高于T-2时的收盘价YT-2、预测收盘价ŶT增长1%，即YT-1＞YT-2、ŶT＞YT-1×(1+1%)，或者预测回报率R PT大于0并且比T-1时的回报率RT-1下降50%，即0＜RPT＜RT-1×50%，则全部卖出。三元股份、圣龙股份、西王食品在2021年6月17日至2021年11月1日期间的收益情况如图8至图10，其中Real表示只根据已知的股票收盘价进行买卖，没有考虑预测收盘价。

从图8至图10中不同趋势股票的回报率曲线图可以看出，通过参考股票收盘价的预测值进行股票交易，能有效提高回报率，降低投资风险，而没有考虑预测的股票收盘价的Real曲线则收益率低，容易造成经济损失。对比三元股份的回报率曲线图8和价格曲线图4可以看出，三元股份估价总体是上升趋势，且增速缓慢，TELM和DTRSI都取得较好的收益率；对比圣龙股份的回报率曲线图9和收盘价曲线图5，可以发现，圣龙股份的股票收盘价在此期间总体是先涨后跌，且在前期上涨阶段价格涨跌波动幅度大，TELM在上涨阶段获得了最大回报率，在后期下跌阶段及时卖出，未造成严重的经济损失；图10和图6分别为西王食品的回报率曲线和收盘价曲线，西王食品的收盘价总体呈现下跌趋势，极易造成经济损失，图10的回报率曲线可以看出，TELM在合适的时间卖出，保证了收益，而DTRSI、EMD-LSTM未能及时止损，造成了严重的经济损失。由此可见，参考TELM预测的收盘价进行投资决策比DTRSI、EMDLSTM预测的股票收盘价更能有效降低股民的投资风险、提高投资收益。不同模型的回报率如表12所示，3个模型中TELM的平均回报率、最低回报率、最高回报率均为最大值。

表12 三种模型的回报率统计Table 12 Return rate statistics of three models %

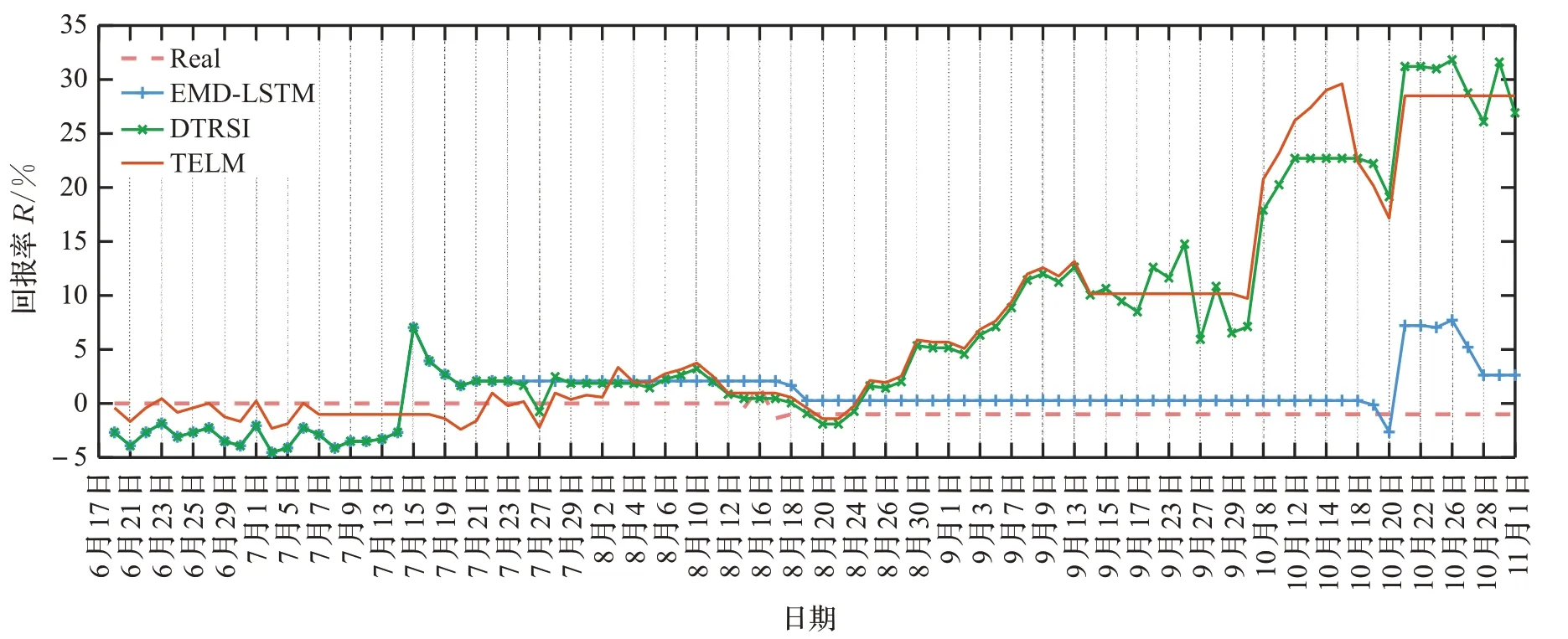
图8 三元股份回报率曲线Fig.8 Sanyuan shares return rate curve

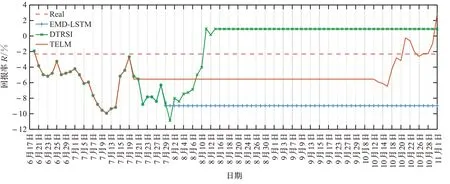
图9 圣龙股份回报率曲线Fig.9 Shenglong shares return rate curve

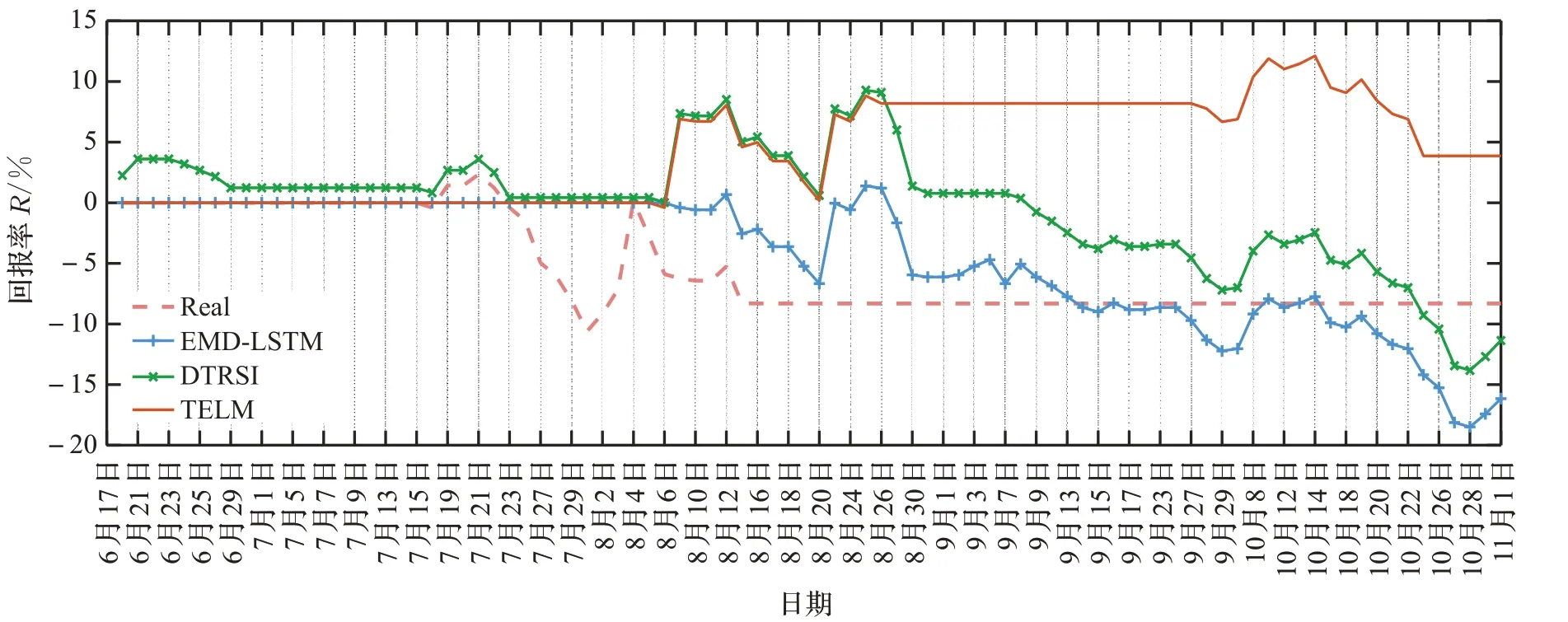
图10 西王食品回报率曲线Fig.10 Xiwang foods return rate curve

表12统计了3个模型的最终遭受了经济损失的股票的占比及其回报率均值和盈利的股票占比及其回报率均值。损失股票占比越高、回报率均值越低说明风险越大，反之，盈利股票占比越高、回报率均值越高，说明该模型的收益越高。3个模型相比，TELM在损失股票占比中最低、盈利股票占比中最高，不同模型的损失回报率均值大小关系为DTRSITELM>EMD-LSTM，即DTRSI具有高风险、高收益，EMD-LSTM具有低风险、低收益，TELM的风险和收益均为中间水平。TELM、DTRSI、EMD-LSTM盈利回报率均值与损失回报率均值的差分别为1.04%、0.17%、0.42%，表明TELM与其他2个模型相比，盈利回报率均值远高于其损失回报率均值，说明TELM在降低了投资风险的前提下，能更大程度提高收益。因此，将TELM预测的收盘价用于股票交易中更能控制投资风险、提高投资回报率。

4 总结

为了充分利用股市内不同股票的价格波动之间的关联性，提高股票的预测效果，本文提出一种基于深度迁移学习的多尺度股票预测模型TELM，用于预测单支股票或指数的收盘价。通过EMD将收盘价数据分解为多尺度分量IMF和RES，从非线性、非平稳的股票数据中捕获股票价格与时间的关系，并利用深度迁移学习的方法训练预测模型，从市场内其他股票的历史数据中提取信息，提高股票的预测效果。实验对500支股票和上证指数、深证成指、上证50、中证500、沪深300进行预测，并根据预测结果模拟股票交易过程。实验结果表明，与MA、LSTM、CNN-LSTM、EMD-LSTM和DTRSI相比，TELM模型能更好地预测股票未来趋势，预测误差更低、拟合效果更好。从行业因素、上市时间、IMF分量个数的角度进行分析发现，通过在预训练数据集中加入某行业的部分股票数据，能有效提升该行业内其他股票的预测效果，并且通过经验模态分解后IMF个数越多，股票的预测效果越好。模拟股票交易过程的实验表明，通过预测股票收盘价能有效提高股票的投资回报率，对股民的投资决策有重要的指导意义。

股票的波动还受经济、政策等因素的影响，如何利用这些因素提升股票的预测效果，是未来可以进一步研究的内容。