改进RRT的二阶段平滑搜索算法
罗 辉,蒋 涛,周 楠,许 林,谭学敏,程永杰
成都信息工程大学 控制工程学院,成都 610000
路径规划算法是机器人和无人驾驶领域的热门研究之一[1-2],是实现导航的关键技术[3],规划算法现目前存在许多问题,例如规划路径不符合车辆实际运动学和动力学约束,以及障碍物贴合拟合路径,算法计算效率不高,拓展性不强等;路径规划算法主要分为两大类,基于图搜索算法,如A*算法,以及基于采样的搜索算法,快速随机搜索树算法等[4]。为了更好地利用A*算法,武善平等人[5]提出一种自适应的启发式A*搜索算法,但是在平滑效率上仍存在路径曲率不连续等缺点。针对机器人在复杂多变的动态环境下的路径规划问题,封硕等人[6]提出了一种融合动态障碍物信息的动态窗口A*搜索算法。由于基于图搜索算法在大规模搜索区域时计算量过大,搜索效率过低。所以后续出现基于采样搜索的算法,能够有效解决图搜索算法在较大规模区域内收敛效率不高的问题。基于采样的搜索算法RRT因其快速的节点拓展机制和强大的搜索性能而被广泛应用[7]。但是传统快速搜索随机数RRT算法存在随机采样、采样的盲目性以及不确定性等问题,导致算法计算效率低下,因此产生了一系列衍生算法来解决这些问题。Mashayekhi等人[8]针对RRT搜索路径时的收敛效率以及优化路径耗时问题,提出了一种Hybird-RRT。冯来春等人[9]提出了一种改进的RRT算法,考虑了车辆当前的环境约束和运动学约束,但是该方法未考虑车辆周围障碍物的约束。针对RRT的实时性以及优化角度等问题,刘紫燕等人[10]提出了一种目标偏向型的平滑RRT算法。Wang等人[11]提出了一种基于弹性带的快速重规划EB-RRT算法,有效地解决了RRT在动态环境中规划的实时性和安全性问题。Hu等人[12]为了有效地提高RRT算法在平滑阶段以及搜索路径长度的质量,提出了一种改进的RRT算法。同时为了更好地解决RRT容易陷入局部最优的问题,Zhang等人[13]提出一种基于复杂环境下的改进RRT算法。Yuan等人[14]提出了一种在三维空间中有效规划路径的改进RRT算法,结合了启发式概率和偏差目标因子,避免算法陷入局部最优的同时,保证了算法在避障规划中的有效性和可靠性。Xiang等人[15]提出了一种针对原快速探索随机树RRT的偏差最优解、非目标和路径非光滑问题,提出了一种改进RRT算法,解决了启发式值函数引起的局部极小问题。为了更好地解决RRT非渐近优化的问题,Karaman等人[16]提出RRT*算法,解决了RRT算法产生的路径并非概率最优解问题,但大规模搜索时运行效率极低。杨瑶等人[17]提出改进双向RRT*路径优化算法,该算法利用Reeds-Shepp曲线优化航向问题。Chen等人[18]针对RRT*收敛速度问题,提出一种结合角度和曲率过滤器筛选父节点的改进RRT*算法。Chen等人[19]提出了一种HL-RRT*算法,解决了RRT*在一些复杂多变的动态环境中的快速收敛问题,同时也缩短了路径的长度。马小陆等人[20]提出了均匀Logistic混沌序列采样的RRT*路径规划算法,解决了RRT*算法收敛速度慢的问题。许万等人[21]提出了简化地图区域采样的思想,加快了RRT*算法的收敛速度。刘成菊等人[22]提出了一种动态规划的方法,减弱了重规划的随机性。但上述所提及的方法并未同时有效解决RRT平滑性差,搜索效率低,以及搜索路径过长等问题。
为有效解决RRT平滑性以及搜索效率,搜索路径长度方面的问题,本文提出了一种二阶段RRT算法(TSRRT),该算法在原RRT算法的基础上,通过分阶段分别融合不同拟合算法进行全局路径规划,来提高算法的收敛速度与规划路径的车辆跟随性。第一阶段,在整个可规划环境范围内采取启发式随机采样,随机采点与结合最大转向角度和曲率的贝塞尔曲线拟合。在曲线拟合时结合车辆最小转弯半径,使改进RRT算法规划的路径更加的平滑,并符合车辆运动的上边界曲率约束,最终产生一条能够满足车辆实际行驶的轨迹。第二阶段,杜宾斯(Dubins)曲线拟合。当第一阶段采样点拓展到目标点邻域内时,直接采用杜宾斯曲线进行连接,并通过碰撞检测,产生一条能够适合于车辆运动轨迹的路径。本文所提出的算法在到达第二阶段起点时,直接通过Dubins曲线连接第二阶段起点到终点的路径,从而减少算法的收敛时间,同时也满足了车辆的模型约束,提高了原有RRT算法的实时性与路径车辆跟随性。通过对比实验验证,TSRRT算法相较于传统RRT算法能取得更好的收敛速度及产生更符合车辆跟随的全局路径,并且TSRRT算法搜索的全局路径满足车辆运动学要求。
1 相关工作
1.1 车辆运动学
传统的RRT路径规划算法仅仅是为了产生一条能够从起点到终点的路径,并没有考虑加入车辆运动学约束使规划的路径能够更好地满足车辆行驶要求,为了让自动驾驶车辆能够更好地对所规划的全局路径进行跟踪,TSRRT算法考虑在路径优化的过程中加入车辆运动学模型约束。算法将全局规划路径的曲率进行优化,使路径曲率能够满足参数连续,从而使TSRRT算法生成的全局路径更加平滑。为了使规划的路径更容易结合车辆运动学模型,本文将车辆运动学模型简化为单车模型,即模型将左右后轮合并为一个N点,即(x,y);左右前轮合并为一个M点;车辆质心为Q点,车辆轴距为L。车辆运动学模型如图1所示,相关参数如表1所示。

表1 车辆运动学模型参数Table 1 Vehicle kinematics model parameters

图1 车辆运动学模型图Fig.1 Vehicle kinematics model diagram
车辆模型的运动学方程如下:

其中,转弯半径与前轮转角存在如下关系:

根据公式(1)和公式(2)得到在当前位置的转弯半径,从而根据曲率和半径的关系得到曲率计算公式:

即,当前位置的曲率可通过当前位置的前轮转角和车辆轴距得到,优化最小转弯半径即优化最大曲率约束,TSRRT算法采用曲线优化算法时融合前轮转角和最大曲率进行车辆运动学优化,让车辆跟踪TSRRT算法所规划路径时更稳定和平顺。
1.2 路径曲率优化
传统的快速随机搜索树算法通常以直线连接两个节点,导致算法全局规划的路径存在转折点的曲率不连续、转折角度过大等问题,所规划的全局路径不适宜进行无人驾驶车辆的轨迹跟踪。本文所提出的TSRRT算法为了保证路径曲率连续[23],采用两段三次贝塞尔曲线来对节点进行连接,同时将车辆的最大转角与贝塞尔曲线的参数相结合,通过优化贝塞尔曲线的相关参数来使得所规划路径的曲率连续且满足无人驾驶车辆的最小转弯半径约束。贝塞尔曲线在路径规划中常用于路径平滑,其n阶贝塞尔表达式如下:

公式(4)中Pi表示第i控制点,n表示贝塞尔曲线的阶数,Bn,i(s)为伯恩斯坦多项式。改进算法TSRRT中第一阶段搜索路径均由两段三阶贝塞尔曲线拼接而成,两段三阶贝塞尔曲线优化路径中的三个节点,如图2所示,其中W1、W2、W3表示所优化的节点,分别为RRT树中的邻近点的父节点、邻近点、新产生的子节点。γ表示无人驾驶车辆的最大转向角度,B0、B1、B2、B3为第一段三阶贝塞尔曲线的控制点,E0、E1、E2、E3为第二段三阶贝塞尔曲线的控制点,d为RRT树的步长。
两条贝塞尔曲线中八个控制点位由下式确定:
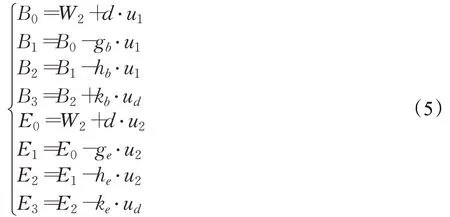
其中,u1、u2、u3分别表示沿着W2W1、W2W3、B2E2方向的单位向量,其余变量为:

根据式(8)的相关常量,可由式(4)计算得到图2中的优化曲线。

图2 三控制点中的贝塞尔曲线图Fig.2 Bezier curve in three control points
1.3 终点范围约束曲线
Reeds_Shepp曲线[24]和Dubins曲线[25]最大的差别是Reeds_Shepp曲线有考虑车辆倒车的情况,而Dubins曲线仅考虑车辆前进的情况。由于全局路径规划并未考虑车辆倒退,所以本文所提出的TSRRT算法采用Dubins曲线进行目标点附近的节点连接。
传统RRT算法以及部分改进RRT算法当搜索到目标点附近时,便以集中采样的方式找到满足特定要求的点,但集中采样易陷入采样迷失终点的困境,且比较耗时,当步长不合适宜时,比较难连接到目标点,也无法满足目标状态的角度约束。而本文所提出的TSRRT算法当有新的节点Znew在目标点附近时,便以满足航向的Dubins曲线连接目标点与点Znew,若该Dubins曲线没有经过障碍物,则算法搜索结束,返回相应的路径,否则继续采样,生成新的节点,添加到树中。
本文受原RRT算法终点结束时判断启发,采用Dubins曲线进行第二阶段曲线连接代替原RRT算法搜索到终点距离范围结束方式。首先是能够有效的在长距离范围内进行满足始端和终端航向的最短路径直连,解决了原RRT在相同终点范围距离的冗余采样和搜索路径过多以及原RRT算法搜索路径不满足航向要求的问题,有效地提高了算法的收敛效率和航向约束问题,同时也结合Dubins曲线满足曲率约束的优点,满足了TSRRT算法在智能车行驶方面的横向控制稳定和舒适性要求。
在原RRT算法中,一般采用当前节点到终点距离小于1倍步长才判定RRT算法已经搜索到终点,但是TSRRT算法是在距离终点10~20倍步长时进行Dubins曲线连接,相比于原RRT算法能够缩短10~20倍步长的距离的随机搜索,有效地提高收敛效率,同时由于原RRT在到达末尾区域时,如果搜索步长和终点范围距离阈值设置不合适,会造成搜索节点和路径过于冗余。所以TSRRT算法采用Dubins曲线能够有效地减少收敛时间,同时Dubins曲线是在满足曲率约束以及规定的始端和末端切线方向条件下,连接两个端点的最短路径,有效地提高了TSRRT算法的收敛效率和满足了路径的航向要求。
Dubins曲线采用Dubins车辆运动模型,即只允许车辆前进,不允许车辆倒退的情况。Dubins曲线是在满足起始状态、末端状态约束与最小转弯半径的情况下,连接二维平面的最短路径。Dubins曲线共有6种可能最短路径,分别为LSL、RSR、RSL、LSR、RLR与LRL,L为以最小转弯半径向左转弯,S为直线行驶,R为以最小转弯半径向右转弯。由于类型太多,本文只列举其中一种情况进行阐述,如图3所示,连接P0、P1两个控制点的最短可能路径RSL,其由直线与圆弧构成,圆弧与直线的连接处相切。

图3 RSL示意图Fig.3 Schematic diagram of RSL
图4为Dubins曲线的应用实验结果,其中深红色曲线为Dubins曲线,其连接第一阶段终点和最终目标点的局部放大图如右图所示,根据计算得出连接处均满足方向角约束,证明改进后的算法TSRRT满足末端状态约束,且曲线具有C1连续性。

图4 改进TSRRT算法末端局部放大图Fig.4 Improved TSRRT algorithm end local enlargement
1.4 快速拓展随机数(RRT)
快速扩展随机树(rapidly-exploring random trees,RRT)算法[26]由美国爱荷华州立大学的LaValle教授在1998年提出,是一种基于采样的快速搜索的规划方法[27],解决了基于图搜索算法中当搜索维度和搜索区域过大时,搜索时间和效率大幅度下降的问题,近十几年得到广泛发展与应用。传统的RRT算法是通过一个初始点作为根节点,进行随机采样,增加叶子节点的方式,生成一个随机扩展树,当随机树中的叶子节点包含了目标点或进入目标区域,便可以在随机树中找到一条由树节点组成的从初始点到目标点的路径[28]。
RRT算法是一种具备概率完备性的增量式采样算法,该算法适合用于解决高维环境与非完整性约束机器人的路径规划问题。原RRT算法通过对状态空间中的采样点进行检测,避免了对搜索空间进行建模,同时在状态空间中随机采样,快速把搜索方向导向空白区域,从而寻找一条从起始点到目标点无障碍路径。拓展树是从状态搜索空间中随机抽取的样本进行逐步构建的,并且本质上倾向于朝向大部分未探测区域进行生长。同时由于它可以轻松处理障碍物和差分约束(非完整性和动力学)的问题,并被广泛应用于自主机器人运动规划。传统RRT算法流程如图5所示,其仿真结果示意如图6,图7表示RRT算法节点拓展细节图,Xrand为随机采样节点,Xnearest为当前树中距离Xrand最近节点,沿XnearestXrand方向拓展一定步长得到Xnew,通过障碍物检测即可加入RRT树。
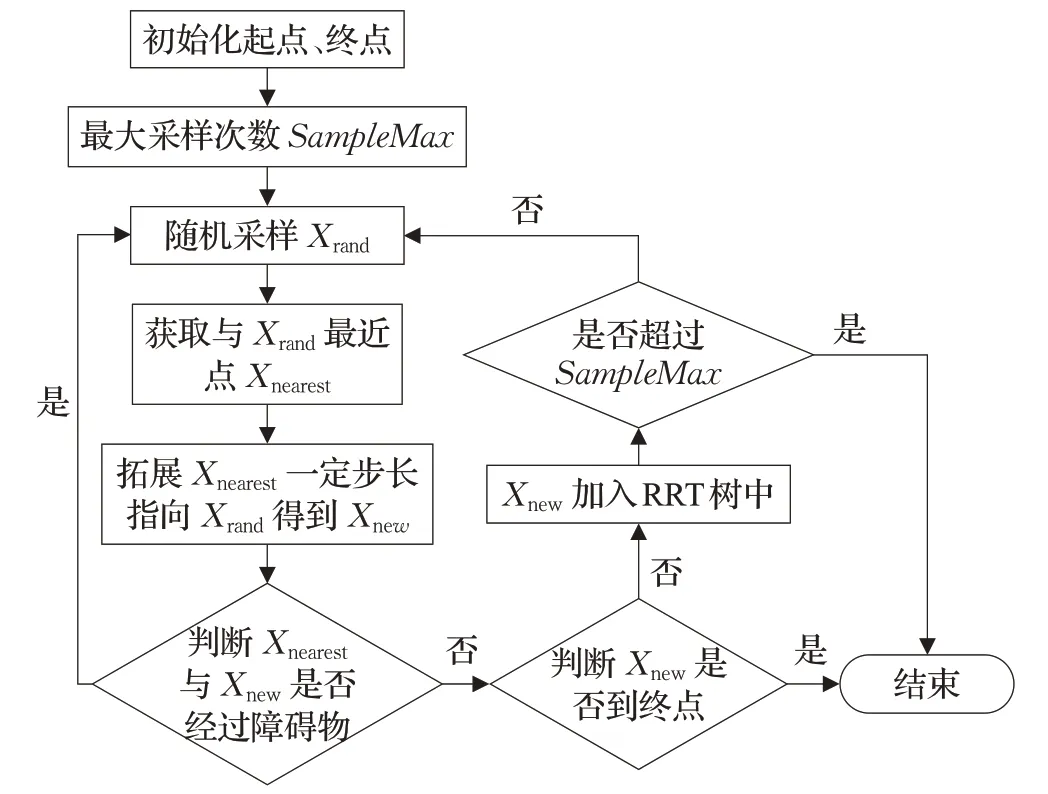
图5 RRT算法流程图Fig.5 RRT algorithm flow chart

图6 RRT搜索示意图Fig.6 RRT search diagram

图7 RRT拓展示意图Fig.7 Schematic diagram of RRT expansion
原RRT算法主要存在以下优点:
(1)RRT算法无需对环境进行建模,适用于高维问题。
(2)RRT算法的随机性虽然存在缺陷,但是算法不容易陷入局部最优。特别是在障碍物较多的情况下,不易陷入局部最优。
(3)RRT算法容易处理障碍物和非完整性约束问题。
(4)RRT算法虽然在路径质量上存在过于曲折,路径非渐近最优,但是其属于概率完备性算法,能够很好地适应各类存在路径解的复杂环境。
由图6与图7以及算法原理易知RRT算法存在以下三个方面不足:
(1)RRT算法产生的路径存在过于曲折,由图6和图7中可以看出,在生成路径的拓展过程中,由于在状态空间随机进行子节点拓展,导致拓展过程中出现较多超过最大转向角度的转折点,则车辆需要在此处停下原地旋转后才能继续前进,故导致该全局路径不适合不能原地旋转的车辆进行路径跟踪或者局部规划。
(2)RRT算法产生路径的时间过于冗长,由于产生大量随机点的同时,也在不停地随机拓展节点,由于搜索节点的随机性和盲目性导致搜索区域扩大,从而产生过长搜索时间。由图6所示,在终点的右上方还有部分搜索树。原RRT算法的冗余搜索部分导致搜索时间过长,现实场景的应用存在局限性,没有达到一定的实时效果。
(3)RRT算法起点的采样容易发生大角度转向甚至反向情况,如图7起点位置处采样所示。当起始采样不符合车辆初始位置航向且超过车辆最大转向角度时,若车辆跟随全局路径,则需要原地转向,但是大部分智能车不能原地旋转。
为了解决上述问题,本文提出了一种TSRRT算法:第一阶段采用原RRT算法结合启发式函数进行快速搜索,到达距离终点10~20步长圆形附近区域;第二阶段采用Dubins曲线直接连接第一阶段的终点和目标点,并判断连接曲线是否经过障碍物,最终到达目标点。经过实验验证,本文提出的TSRRT算法可以快速地搜索出一条同时满足安全与运动学约束的平滑路径。
2 二阶段RRT(TSRRT)算法
2.1 虚拟起始节点
传统RRT算法没有对起始航向进行约束,即在起点后的第一个新节点可以在360°的范围内产生,由于智能车本身是具备朝向信息的,即在起点时有航向信息,如果不进行航向约束,则存在较大概率的采样点不符合起始航向,导致车辆需要原地旋转才能满足路径的航向约束要求。所以为满足起始状态的角度约束,增加距离车辆起点航向的一个步长距离的虚拟节点Zfstart作为第一个采样点,同时将其加入到TSRRT搜索树T中,作为树T的起始节点。起点位置采样方式如图8所示。
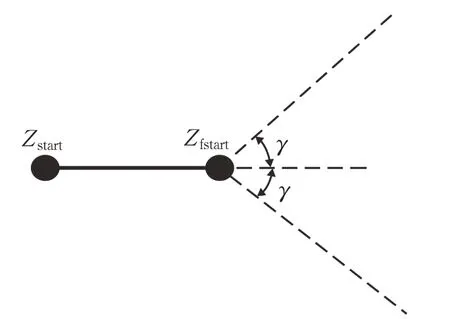
图8 起始位置采样图Fig.8 Start position sampling diagram
2.2 邻近节点优选
原RRT算法拓展节点时采用欧氏距离方式找到最优邻近节点,当节点数量较多时,容易产生大量计算从而耗时。而改进算法TSRRT采用搜索随机节点周围固定K个邻近节点方式,保证当节点数过多时也不会产生较多计算量,从而提高算法的收敛速度。改进算法TSRRT首先采用随机搜索策略进行节点采样,同时融合启发式函数进行周围K个邻近节点代价值计算,G为当前总代价值最小的邻近节点:

其中,H(Q)为起始位置到当前邻近节点位置的已花费代价值,H(G)用于计算从当前邻近节点位置到目标点的预估代价值:

Lbci为第i邻近节点与其父节点的贝塞尔曲线近似长度,公式(12)中n为贝塞尔曲线的阶数,Lc为贝塞尔曲线的弦长,Lp为贝塞尔曲线相邻点之间的距离,以三阶贝塞尔曲线为例,如图9所示。

图9 Bezier曲线连接图Fig.9 Bezier curve connection diagram
公式(12)中的Lc和Lp计算公式如下:

预估代价值H(G)为当前邻近节点到目标点的Dubins曲线连接长度。初始节点Zfstart的已花费代价值设置为0。公式(10)既考虑到了当前邻近节点的已消耗代价,同时也计算了该邻近节点的预估代价值,能够快速找到随机点周围固定K个距离代价值较小的邻近节点,将这些节点按代价值进行升序排序,再依次判断该采样节点和邻近节点以及邻近父节点合成的角度是否超过最大转向角度,当获取到没有超过最大转向角度γ的邻近节点时,则选取该邻近节点作为随机采样点的父节点,然后进行节点拓展,而原RRT算法计算邻近节点时,采用欧式距离选取整棵RRT树中最近的节点作为邻近节点,当搜索空间过大时,其选取邻近节点的计算量会大幅度增加,导致收敛效率过低,相比于改进算法TSRRT搜索邻近节点方式,原RRT算法邻近节点选取方式存在条件判断不足,计算量过大等缺陷。
2.3 障碍物检测
本文结合栅格地图与贝塞尔曲线的凸包性质做障碍物检测,贝塞尔的凸包性即贝塞尔曲线一定在其控制点所围成的最小凸多边形内,如图10所示。该地图提供地图中任意一点到其最近障碍物的距离与到最近的泰森多边形边的位置。如图10所示,为保证两段贝塞尔曲线不在障碍物中,两段贝塞尔曲线分别做障碍物检测,以第一段贝塞尔曲线为例,只需保证其凸包内的任意一点均不在障碍物内即可,即dh>0。Pobs表示离贝塞尔曲线控制点最近的障碍物且dc表示相应的距离,Pr表示贝塞尔曲线凸包内任意一点,rh表示该控制点到Pr的距离,r01、r12、r23分别表示相应控制点之间的距离。

图10 碰撞检测示意图Fig.10 Schematic diagram of collision detection
由三角不等式易得:

根据公式(18)即可判断当前Bezier曲线部分是否避开障碍物。
2.4 TSRRT算法
TSRRT算法流程图如图11所示。
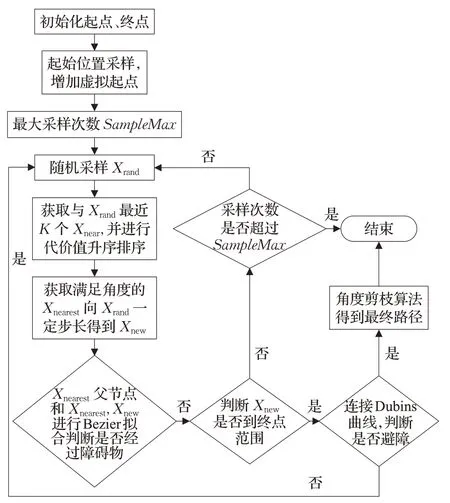
图11 TSRRT算法流程图Fig.11 TSRRT algorithm flow chart
TSRRT算法主要以提高原算法搜索效率和让搜索路径满足车辆的运动学规律为目的。TSRRT算法分为两个阶段,第一阶段是结合原RRT算法搜索方式进行随机采样,保留原RRT算法的拓展状态空间的随机性,避免陷入局部最优。其次采用代价值方式查询采样节点周围固定K个邻近节点,相比于原RRT算法进行除采样节点以外的所有节点进行计算筛选的方式,此改进算法不会随着搜索树节点的增多而增加计算量,所有能够更高效地找到邻近节点。同时算法采用启发式函数进行搜索,能够更快地让搜索方向趋于目标点方向,有效地提高TSRRT算法第一阶段的收敛效率。TSRRT算法在搜索邻近节点的同时采用已消耗代价和预估代价的启发式函数以及角度剔除计算方式,相比于原RRT算法找欧式距离最近节点的方式能够更加精准地找到角度和距离合适的邻近节点,有效地提高TSRRT算法的收敛精度。当完成搜索后融合两段三次Bezier曲线进行拟合以及障碍物检测之后,保证了搜索路径曲率连续以及路径的安全性,让车辆在行驶过程中能够以不停车的方式进行连续平稳安全地转向。第二阶段采用不同于原RRT算法方式的直连算法,这也是第一次提出利用Dubins曲线快速连接第一阶段终点和目标点的方式,极大地提高了RRT算法的收敛速度,同时也满足了车辆的航向约束。最终完成一、二阶段搜索之后进行角度检测算法剪枝,完成路径搜索。
相较于传统的RRT算法,TSRRT算法有以下五个部分进行改进:
(1)起始点增加虚拟节点如图8所示,满足车辆起始位航向搜索,避免算法在起始位置搜索随机性问题,从而避免让车辆在原地旋转后跟踪路径。
(2)增加距离和角度以及曲率代价值启发式搜索如公式(9)所示,快速搜索出代价值最低且满足角度约束的邻近节点,提高了邻近节点的搜索效率以及邻近节点质量,不再是以单纯的欧式距离作为度量方式,使算法能够快速收敛,同时提高路径搜索质量。
(3)增加结合最小转弯半径和最大转向角度的两段贝塞尔曲线如公式(4)所示进行曲率优化,保证路径曲率连续,从而能够让车辆在不停止运动的情况下进行连续转弯,满足车辆运动学规律。
(4)增加Dubins曲线如图4所示,当算法搜索到终点范围10~20倍步长时直接连接Dubins曲线,提高了TSRRT算法搜索效率,Dubins曲线既保证了起始点和终止点间的距离最短,同时满足曲率约束也满足了车辆在起始点和终点航向约束要求。
(5)最后通过剪枝算法得到路径:存在P0、P1、P2、P3、P4节点,分别计算∠P1P2P4和∠P2P4P5的角度是否同时超过最大转向角度,若没有超过,并且通过障碍物检测,即可删除P3节点,否则继续下一节点判断。
本文提出的TSRRT算法第一阶段是结合原RRT算法搜索方式进行随机采样,保留原RRT算法拓展状态空间的随机性,避免陷入局部最优。第二阶段采用Dubins曲线直连方式约束曲率以及始端和终端的航向,同时也是始端和终端间的最短路径。相比于原RRT算法仍需在此阶段进行随机搜索,由于其随机性搜索拓展以及较长路径需要探索,使其在此阶段搜索时间将比TSRRT算法搜索时间更多,同时原RRT算法搜索路径时采样的随机性导致拓展路径过于曲折,也不满足路径的航向和曲率要求。所以TSRRT算法在两个阶段均能够有效地提高算法的搜索效率,同时由于启发式搜索和Dubins曲线的路径最短特性,能够有效地提升路径的质量,缩短路径的长度,从而提高TSRRT算法整体的收敛精度。
3 实验
3.1 实验设计
为了充分研究所提出算法的有效性,实验主要考虑以下三个场景,分别是简单障碍物场景、复杂随机障碍物场景(考虑有人或者其他障碍物出现)、迷宫类障碍物场景。地图大小为500 m×500 m,目标偏置率Pgoal=0.2、最大曲率kmax=0.1、最大转向角γ=0.4π、采样步长d=10.08,起始点和终点设置如表2所示。
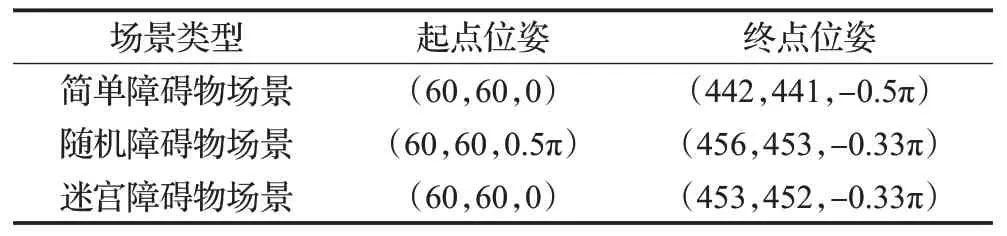
表2 三种场景状态设置表Table 2 Three scene states setting table
3.2 实验结果
3.2.1 简单障碍物场景实验结果
简单障碍物场景路径搜索结果如图12所示,其中图(a)红色曲线为传统RRT方法搜索结果。图(b)为TSRRT在相同条件下的实验结果,红色曲线为第一阶段搜索结果,深红色曲线为第二阶段搜索结果。从实验结果可以看出TSRRT算法搜索路径长度明显变短,并且平滑度上明显优于传统RRT算法结果。
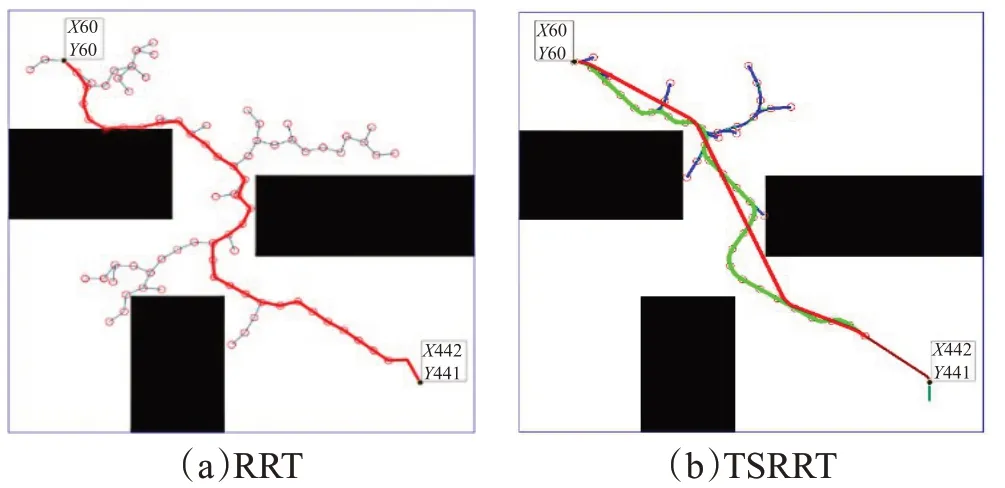
图12 简单障碍物场景路径搜索结果图Fig.12 Path search results of simple obstacle scene
为了更好地展示所提出TSRRT算法对于路径平滑的有效性,将对比的两种方法所生成路径的曲率变化展示如图13所示。其中图(a)为传统RRT方法生成路径的曲率变化情况,图(b)为TSRRT方法所生成路径的曲率变化情况。横坐标代表曲率在整条路径相应比例位置,纵坐标代表曲率。从实验结果看出传统RRT方法最大曲率已经超过0.1,而TSRRT方法并没有超过0.035,同时传统RRT搜索路径曲率突变过多,而TSRRT算法搜索路径曲率连续。

图13 简单障碍物场景路径曲率变化图Fig.13 Path curvature variation of simple obstacle scene
将两种对比方法的相关性能指标展示如表3所示,其中各项数据为100次实验结果的均值。从表中可以看出传统RRT与TSRRT算法均能在1 s内找到有效的路径,但传统RRT算法的路径偏长,而TSRRT算法搜索路径长度减少了23.60%;TSRRT算法采用启发式搜索和Dubins曲线连接第一阶段终点和目标点,提高了算法搜索效率和搜索质量,平均耗时减少40.38%,扩展的节点数减少31.49%。

表3 简单障碍物实验结果表Table 3 Experimental results of simple obstacles
3.2.2 随机障碍物场景实验结果
随机障碍物场景实验结果如图14所示。图(a)为传统RRT方法实验结果,最终搜索路径如红色曲线所示。图(b)为TSRRT在相同条件下同场景的实验结果,红色路径为第一阶段搜索结果,深红色路径为第二阶段搜索结果。改进RRT算法明显在路径点角度和搜索路径长度上优于传统RRT算法。
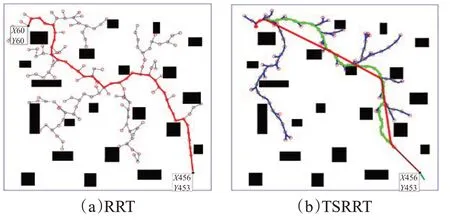
图14 随机障碍物场景路径搜索结果图Fig.14 Path search results of random obstacle scene
传统RRT算法生成路径的曲率变化如图15(a)所示,TSRRT算法生成路径的曲率变化如图15(b)所示。从实验结果看出原RRT算法已经多次超过最大曲率0.1,小于车辆最小转弯半径,而TSRRT算法并没有超过0.071。同时由于原RRT搜索路径曲率突变过多且超过0.1,造成车辆跟随时需要在该点位停下进行原地旋转,而TSRRT算法搜索路径曲率连续,车辆无需在原地旋转即可进行平滑稳定的转向,满足了车辆运动学稳定舒适的横向控制要求。

图15 随机障碍物场景路径曲率变化图Fig.15 Path curvature variation of random obstacle scene
随机障碍物实验场景下的算法性能指标数据如表4所示,其中各项数据指标为100次实验结果的均值。从表中可以看出传统RRT算法、TSRRT算法均能在1 s内找到有效的路径,但是传统RRT算法的路径偏长,TSRRT算法搜索路径长度减少了23.81%;改进后的TSRRT算法采用启发式搜索和Dubins曲线连接终点,平均耗时减少42.80%,扩展的节点数减少21.83%。实验结果证明提出的RRT改进方式应用于随机障碍物场景有效。

表4 随机障碍物实验结果表Table 4 Results of random obstacle experiment
3.2.3 迷宫障碍物场景实验结果
迷宫障碍物场景实验结果如图16所示。图(a)红色路径为传统RRT方法搜索实验结果。图(b)为TSRRT算法在相同条件下的实验结果,红色路径为第一阶段搜索结果,深红色路径为Dubins曲线直连结果,从实验结果可以看出改进后的算法TSRRT在搜索路径的长度上明显变短,并且平滑度上明显优于RRT算法。
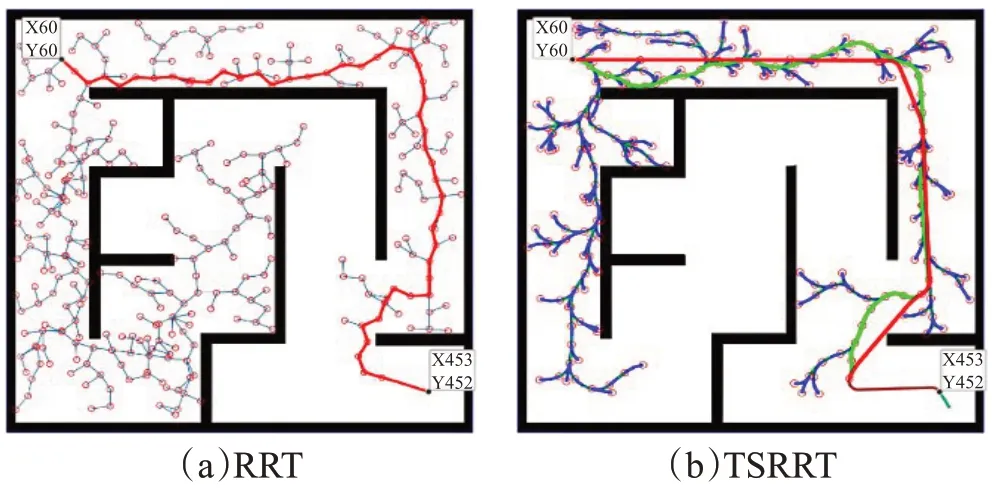
图16 迷宫障碍物场景路径搜索结果图Fig.16 Maze obstacle scene path search results
传统RRT算法生成路径的曲率变化如图17(a)所示,TSRRT生成路径的曲率变化如图17(b)所示。从实验结果看出传统RRT算法已经多次超过最大曲率0.1,而改进后的算法TSRRT并没有超过0.075,同时原RRT搜索路径曲率突变过多,而TSRRT算法搜索路径曲率连续,从而让车辆能够平滑稳定的转向,不再需要停止原地旋转。实验结果证明提出的RRT改进方式应用于随机障碍物场景有效。
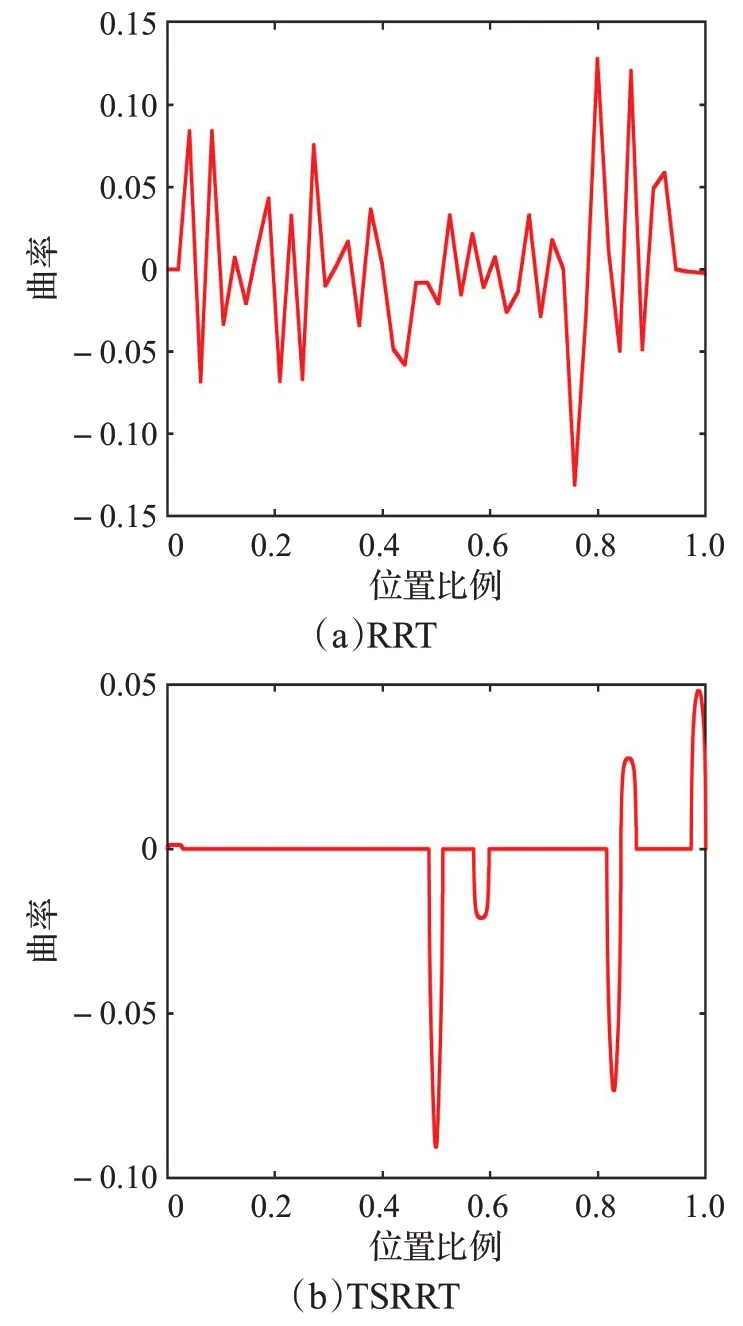
图17 迷宫障碍物场景路径曲率变化图Fig.17 Path curvature variation of maze obstacle scene
迷宫障碍物实验场景下的算法性能指标数据如表5所示,其中各项数据均为100次实验结果的均值。从表中可以看出传统RRT、改进后的算法TSRRT均能在1 s内找到有效的路径,但是传统RRT算法的路径偏长,TSRRT算法搜索路径长度减少27.66%;改进后的算法TSRRT采用启发式搜索和Dubins曲线连接终点,平均耗时减少46.05%,扩展的节点数减少33.75%。由于两种算法均采用目标偏置采样的策略,所以在迷宫环境下,能快速找到有效路径。实验结果证明提出的RRT改进方式应用于迷宫障碍物场景有效。

表5 迷宫障碍物实验结果表Table 5 Maze obstacle test results
3.3 实验总结
从三个场景实验结果可以得出:TSRRT算法相比于原RRT算法,TSRRT算法搜索的路径能够在横向控制进行更好的优化,因为其能够搜索出一条曲率连续的全局路径,能够让智能车在不停车的情况下进行连续平稳的横向控制,然而原RRT算法搜索的路径曲折,产生超过车辆最小转弯半径的控制点,路径点转折角度过大且频繁变向,曲率不连续,导致智能车在跟随过程中会出现较大转向角度波动以及横向控制波动,容易出现车辆控制不平稳,刹车掉头转向等问题。
从实验结果中的表格可以得出,原RRT算法采用随机性搜索时,会产生较多的冗余节点,导致算法计算时间增加,同时也产生了一条不符合曲率和航向约束的路径,不能满足智能车的运动学要求。而TSRRT算法在第一阶段采用启发式函数引导式搜索以及K个固定邻近节点选取,有效地提高了邻近节点的选取效率,同时也让搜索方向能够更快地偏向目标点区域。第二阶段Dubins曲线直连第一阶段终点和目标点,删除了原RRT算法在终点范围的随机搜索方式,有效地减少了算法的收敛时间,同时Dubins曲线也是满足始端和终端航向以及曲率约束的最短路径,而RRT在终点区域搜索时因其随机性而不能保证是最短路径,并且不满足航向以及曲率要求,所以TSRRT算法有效地提高了原RRT算法的搜索效率和搜索质量。
4 结束语
本文针对原RRT算法存在搜索路径过于曲折,不满足车辆运动学约束,路径搜索实时性不高,以及搜索路径过于冗长等问题,提出了一种二阶段RRT算法(TSRRT),该算法融合最大转向角度的三次Bezier曲线进行路径曲率优化,使生成的路径满足车辆运动学约束。与此同时TSRRT还进行分阶段引导式采样搜索与Dubins曲线直连以及最大转向角剪枝,增强算法搜索实时性和缩短路径长度。通过三种仿真场景对比实验验证得到,本文所提出的TSRRT算法在搜索时间上比原RRT算法平均节省近43%,能够更加快速地实现全局路径搜索,并且搜索出的全局路径长度平均减少25%,同时全局路径曲率连续,能够让车辆在不停车的情况下连续平稳地转向,因此能够满足车辆运动学约束,以便智能车辆更好地进行路径跟踪。

