工程机械液压过滤器实际寿命的破解思路

崔本涛，金 涛，耿 聪，熊丽媛

（1.新乡航空工业（集团）有限公司，河南新乡 453000；2.航空工业（新乡）计测科技有限公司，河南新乡 453019）

0 引言

过滤器是工程机械液压系统中维护频次最多的产品，对滤芯实际寿命[1]的预知评定对指导过滤器维护非常重要。在工程机械、航空、航天、船舶和汽车等工业领域，预知滤芯使用寿命[2]的探索和研究工作，目前形成的一系列的国家、国家军用和行业标准有一个共同的特点：无论是纳污容量[3]或是试验时间[4]对滤芯实际使用寿命的评定都无关联，无法帮助人们准确知晓实际的工作时间。对特殊工程机械液压系统，准确评定滤芯的实际寿命，对制定科学的维护计划意义重大。本文针对此问题对滤芯的实际寿命进行科学地评定[5]。

滤芯的寿命有两种定义：一是实际寿命，即使用寿命或使用时间；二是实验室寿命，即实验室堵塞寿命[6]的试验时间。但是实验室寿命并不代表实际寿命。因为试验用的人造粉尘是标准粉尘[7]，拥有较好的粒度分布和一致性。实际污物的构成是非常的复杂，很难全面、准确掌握其污染的成分与分布，并且滤芯多次通过纳污容量、堵塞寿命等试验，在试验过程中是连续不可中断的，如果因停电突发中断试验，则试验失败。

目前，行业内围绕滤芯实际寿命的探索，基本停留在液压过滤器和汽车“三滤”行业的“纳污容量”“视在纳污容量”“实际纳污容量”“容尘量”“试验时间”“堵塞寿命”等概念的认知上，这些数据并不能指导过滤器的维护周期[8]。因此，本文开展滤芯实际寿命的预知研究思路分为以下3项。

（1）配制“实际污染物”代替标准粉尘在实验室获得滤芯寿命。在机械设备油液系统中取样分析只能获得部分的金属或非金属成分，有关污染物的分布与定量，尤其是油液受高压剪切和高温交变产生的化学污染物、细菌及未知的污染物很难获知[9]。目前用收集实际污染物，在实验室获得滤芯寿命的方法无法实现。

（2）针对流量、压力、温度、使用环境及油液污染度等变量，研究滤芯单位过滤面积的寿命系数，然后推算出滤芯全过滤面积的使用寿命。该思路同样会遇到人造粉尘不能代替“实际污染物”的问题。

（3）利用压差相等原则，结合试验和实际使用的数据通过数学方法建立数学模型，研究实验室寿命与实际寿命的内在关系。

《液压传动 滤芯 实际寿命评定指南》，现已立项为国际标准ISO∕AWI TR 12144[10]。

1 滤芯实际寿命评定理论依据

破解滤芯实际寿命评定的理论依据有3 个：滤芯压差相等原则、拟合建模的有效性判定及实际寿命的评定模型。

1.1 滤芯压差相等原则

1.1.1 物理意义

假设工程机械流体系统和实验室试验系统油液中污染物的浓度是相对稳定的，在工作与试验条件相同时，影响滤芯的压差升高的变量就是时间的唯一函数。即滤芯的实际压差升高多少，取决于使用时间的长短；滤芯的试验压差升高多少，取决于试验时间的长短，则式（1）就会成立。

式中：Δp滤芯的压差，kPa；T为实际使用时间，h；t为试验时间，h。

1.1.2 Δp-T-t蜘蛛网图

图1所示为基于滤芯压差相等原则创立的实际寿命-试验时间与压差的关系图，叫做Δp-T-t蜘蛛网图。曲线Ⅰ是压差随实际使用时间升高的变化关系；曲线Ⅱ是压差随试验时间升高的变化关系；在流量-压差相同时，由曲线Ⅰ关联对接曲线Ⅱ，则可以得到曲线Ⅲ，即实际使用时间与试验时间的对应关系。这是实际寿命与实验室寿命内在关系的理论依据。

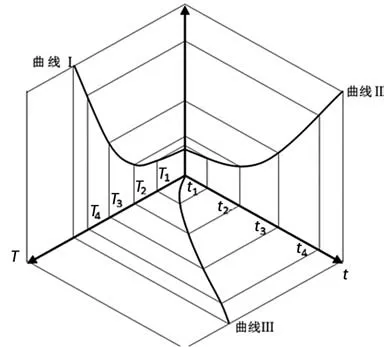
图1 实际时间-试验时间与压差的关系

1.2 拟合建模有效性判定

1.2.1 实际寿命数学模型

（1）数据获取

获取滤芯实际使用数据的途径有2 个：一是直接获得，二是间接获得。

直接获得：现场在线检测压差、工作时间、工作流量、工作温度和污染度，直接得到不同使用时间Ti（i=1，2，3，…，n）所对应的工作压差Δpi（i=1，2，3，…，n），如表1所示。

表1 实际使用时间对应的压差

间接获得：针对指定的工程机械设备，有计划收回不同使用时间Ti（i=1，2，3，…，n）的滤芯，将不同的使用时间进行分组，参考滤芯实际工作流量与温度（黏度影响）在实验室，参照ISO 3968：2001 测得Δpi（i=1，2，3，…，n）。

（2）拟合曲线

根据表1 中的时间与压差，用不少于4 组（组数越多越精确）的数据拟合成连续曲线Ⅰ，如图2所示。

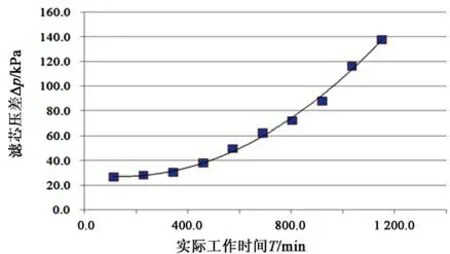
图2 滤芯压差与实际工作时间拟合曲线

（3）数学模型

根据滤芯压差与实际工作时间的关系曲线Ⅰ进行回归建模，得到实际寿命拟合回归的数学模型，如式（2）所示。

式中：T为滤芯的实际寿命，h；Δp为滤芯元件的压差，kPa；A、B分别为拟合常数；M为拟合对数的指数，一般情况下M=0、1或2。

1.2.2 实验室寿命的数学模型

（1）数据获取

根据特定工程机械所用滤芯的实际工作流量（平均流量），参照ISO 16889 方法向试验系统添加ISO FTD 试验粉尘[11]，用全新滤芯分别测得在压差为Δpi（i=1，2，3，…，n）时的实验室寿命为ti（i=1，2，3，…，n），如表2所示。同时测出过滤比β5、β10[12]及污染度等级[13]。

表2 实验室寿命对应的压差

（2）拟合曲线

根据表2中的实验室寿命与压差，用不少于4组（组数越多越精确）的数据拟合成连续曲线Ⅱ，如图3所示。

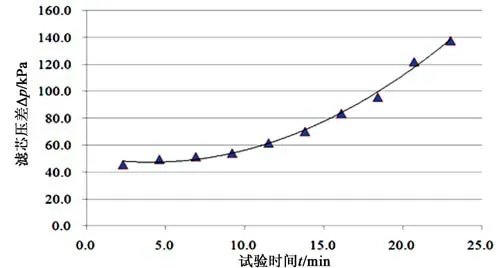
图3 滤芯压差与试验时间拟合曲线

（3）数学模型

根据滤芯压差与实验室寿命的关系曲线Ⅱ进行回归建模，得到实验室寿命拟合回归的数学模型，如式（3）所示。

式中：t为滤芯元件的实验室寿命，h；Δp为滤芯元件的压差，kPa；a、b分别为拟合常数；m为拟合对数的指数，一般情况下m=0、1或2。

1.2.3 实验室寿命模型的有效性判定

实际寿命（式（2））和实验室寿命（式（3）），是通过寻找适当的连续曲线来拟合观测“时间-压差”多组离散数据的对应关系，据此求得更加近似的拟合曲线后，再利用线性回归分析方法建立的数学模型。

实际寿命和实验室寿命与滤芯压差的关系未必都是相同的曲线关系，只有当两者的拟合曲线类似、趋势相同时，建立的数学模型才可用来评定预估滤芯的未知寿命。当拟合指数M=m时，建立的数学模型有效。

（1）直线拟合曲线

当M=m=0时，滤芯的实际寿命和实验室寿命与流量压差拟合的曲线均为直线斜线，变化趋势类同，建立的实验室寿命数学模型是有效的。根据式（3）可得实验室寿命的计算方法如式（4）所示：

（2）对数拟合曲线

当M=m=1时，滤芯的实际寿命和实验室寿命与流量压差拟合的曲线均为对数曲线，变化趋势类同，建立的实验室寿命数学模型是有效的。根据式（3）可得实验室寿命的计算方法如式（4）所示：

（3）双对数拟合曲线

当M=m=2时，滤芯的实际寿命和实验室寿命与流量压差拟合的曲线均为双对数曲线，变化趋势类同，建立的实验室寿命数学模型是有效的。根据式（3）可得实验室寿命的计算方法如式（6）所示：

（4）异类拟合曲线

当M≠m时，滤芯的实际寿命和实验室寿命与流量压差拟合的曲线不是同类曲线，变化趋势也不相同，建立的实验室寿命数学模型是无效的。

为解决数学模型的有效性问题，可从以下两个方面分析原因：针对实际使用状态存在的原因进行分析，重新采集实际使用数据；试验粉尘与滤芯过滤性能可能不匹配等问题。

1.3 实际寿命的评定模型

滤芯实际寿命的评定模型有两种：一是直接评定模型，二是间接评定模型。

1.3.1 直接评定模型

用实际使用数据拟合回归建立的数学模型是直接评定模型，其评定滤芯预知寿命的方法叫直接评定法。即将不同工作压差代入实际寿命数学模型式（2），可直接求出预知的实际寿命。

直接评定的优点是针对性强，评定的预知结果准确，相对偏差小。缺点是需要现场配备在线检测能力，只能一对一地评定，对工作流量不同的滤芯不适用；如果系统污染度控制水平[14]不稳定，则评定结果的重复性比较差。

1.3.2 间接评定模型

利用实验室寿命模型评估实际寿命的模型是间接评定模型，如式（7）所示，其评定滤芯预知寿命的方法叫间接评定。即根据有效性的判定，用式（4）～（6）先计算出滤芯极限压差或某压差下的实验室寿命t后，再按照式（7）求出滤芯同等流量条件下的实际寿命T：

式中：T为滤芯元件的实际使用寿命，h；N为实际工况下油液的污染度等级（ISO 4406）；T为滤芯元件的实验室寿命，h；n为试验条件下油液的污染度等级（ISO 4406）。

其中，式（7）中的n-N取ISO 4406[15]对应的3 个污染度等级差值结果的最小值；实验室试验的油液温度根据实际工况的温度进行控制。

间接评定的优点是在实验室便于获得不同流量的实验室寿命模型，针对不同的滤芯对象视情开展研究评定，对同类的滤芯根据使用条件也可参考评定；缺点是对全寿命周期评定结果的相对偏差较大，时间周期与成本较高。

2 评定滤芯实际寿命的试验验证

用2 件滤芯开展试验验证，1#件实施实际寿命的在线实测，2#件进行实验室寿命的检测试验。

2.1 直接评定法的验证实践

2.1.1 在线实测结果与拟合曲线

1#件在线实测条件：油液46 号液压油，工作流量、温度、被实测过滤器的进、出口油液的污染度（ISO4406）和累计的使用工作时间等参数数据均为在线实时检测并记录，滤芯的过滤比β5≥100、β10≥200。现场在线实测获得的部分数据如表3所示。

从表3 序号1 至序号10 的10 组数据中可以看出，1月16 日下午13:06:58 系统刚启动时油温26 ℃相对较低，滤芯压差24 kPa 相对较高，随着工作时间的延长，油温逐渐升高、压差缓慢下降，当工作到0.81 h 时油温升到28.36 ℃、滤芯压差稳定在22 kPa，工作流量基本控制在45 L∕min 的水平。开启测试系统，在流量不变时压差偏高的现象是启动油温偏低造成的，当油温升高稳定后对压差的影响起决于滤芯拦截污染物的多少。这种现象记录在图4 实时检测的曲线中，每次启动时由于油温偏低引起压差偏高，随着工作时间延长，压差回落到接近上次工作的水平再继续缓慢升高，随着启动工作次数的递增及累计使用时间的增长，滤芯拦截的污染物持续增多，压差连续增大。序号40 到序号570，是每次启动工作压差回稳的记录数据。

将表3 中的数据进行整理，并结合图4 将滤芯压差与累计工作时间拟合成连续的曲线，如图5所示。

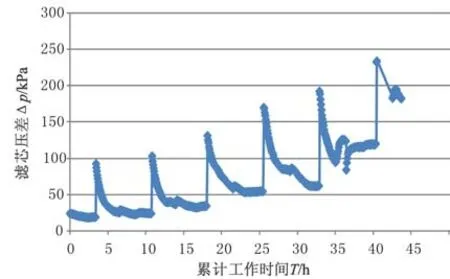
图4 滤芯1#在线实时检测的压差与时间记录曲线

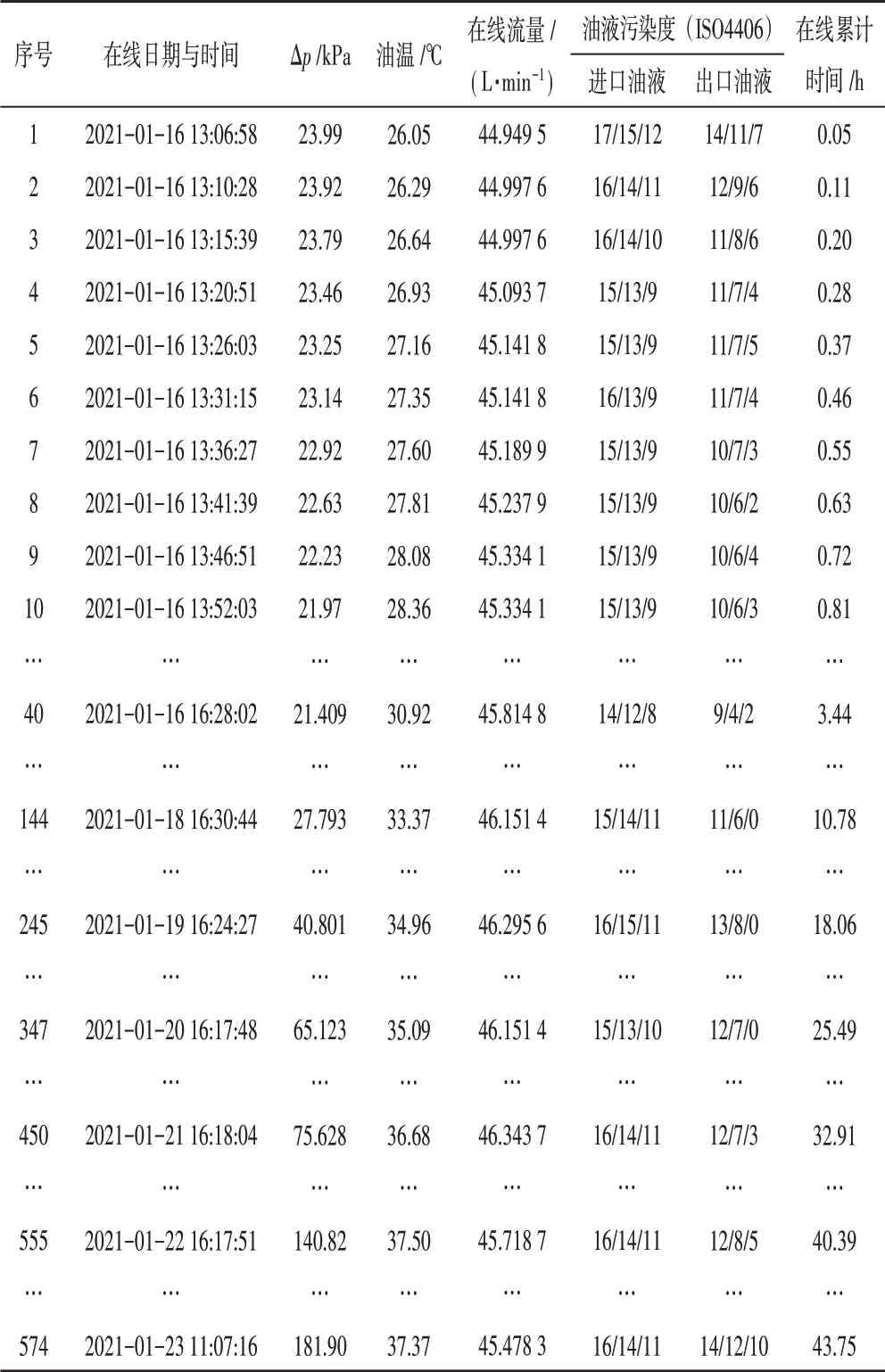
表3 滤芯1#在线实测的数据

2.1.2 滤芯1#在线实测建立的数学模型根据图5 拟合曲线建立的滤芯实际寿命T与压差Δp的数学模型如式（8）所示，其中拟合对数指数M=2，系双对数函数；相关系数R2=0.983 2，说明拟合曲线与在线实测的曲线高度近似。

图5 滤芯1#实时检测压差与时间拟合曲线

2.1.3 直接评定滤芯1#实际寿命

基于相同工作条件，将不同的压差代入式（8），就可直接推算滤芯1#对应的实际使用寿命，其寿命的评定值与在线实测寿命的相对偏差如表（4）所示。表中可见，用在线实测结果拟合建立的模型直接评定的寿命，其相对偏差较小，最小2%左右，最大不超过20%。

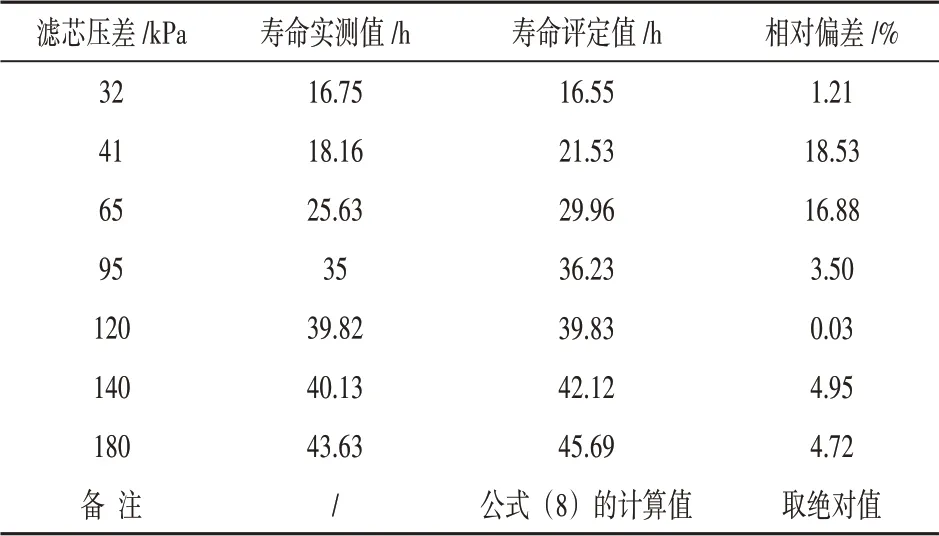
表4 实际寿命直接评定结果的相对偏差

2.2 间接评定法的验证实践

2.2.1 实验室寿命的测试与拟合曲线

对滤芯2#参照国际标准ISO 16889 用添加粉尘的方法测试实验室寿命。油液温度、流量参考在线实测相同条件分别控制在35 ℃±2 ℃和45 L∕min，粉尘为细粉尘ISO FTD、浓度5 mg∕L，终止压差200 kPa，试验油液为15 号航空液压油[16]。随着添加粉尘的增加所测得实验室寿命及压差等数据如表5所示。

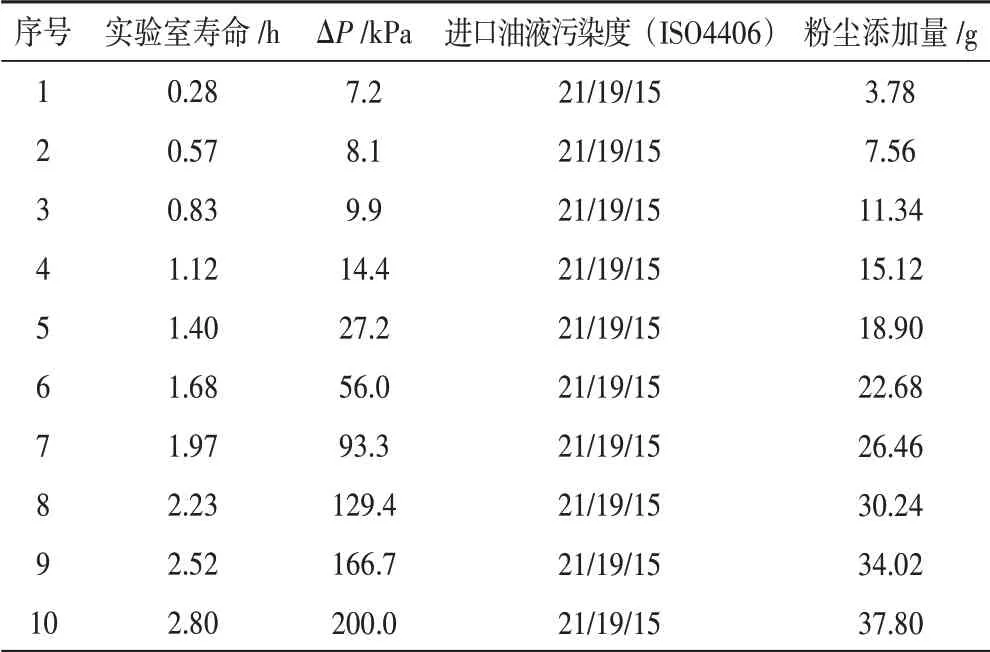
表5 滤芯2#的实验室寿命及压差

将表5 中的数据进行整理并拟合成连续的曲线，如图6所示。

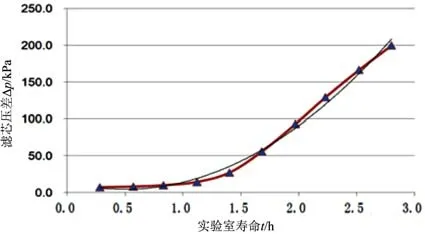
图6 滤芯2#试验压差与实验室寿命拟合曲线

2.2.2 实验室寿命的数学模型与有效性判定

根据图6 拟合曲线建立的实验室寿命t与压差Δp的数学模型如式（9）所示，其中拟合对数的指数m=2，系双对数函数；相关系数R2=0.962 4，说明拟合曲线与实验检测的曲线高度近似。

从式（8）～（9）中可见：拟合指数M=m=2，两者均系双对数函，即实验室寿命的数学模型有效。

2.2.3 间接评定滤芯1#的实际寿命

基于同流量、同温度条件下的等压差原则，滤芯1#在线实测与滤芯2#实验室测试的进口油液污染度差值最小值n-N=4，那么用式（7）和式（9）间接评定滤芯1#的实际寿命，其评定结果与相对偏差如表6 所示。从表中可见，在32～65 kPa 的低压差段，间接评定滤芯寿命的误差比较大，最大超过50%；在95～140 kPa 的中压差段，间接评定滤芯寿命的误差比较小，不超过8.3%；在180 kPa 的高压段，间接评定滤芯寿命的误差稍微增大，超过了10%。

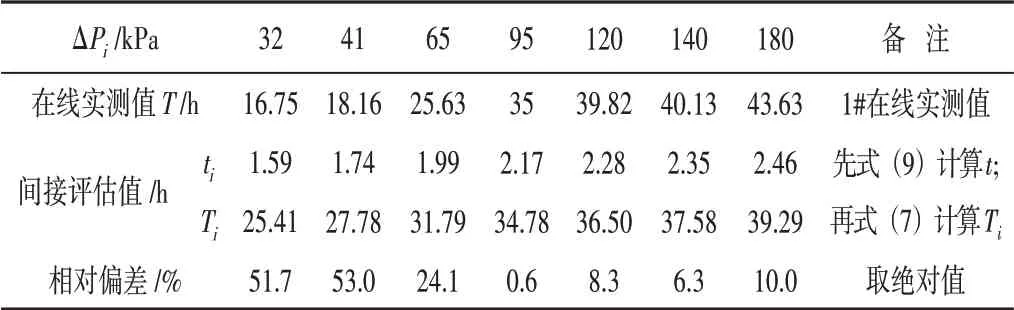
表6 用2#实验室寿命模型评定1#实际寿命的误差

在滤芯的寿命周期内，开始使用时的压差随时间增长变化不大，压差增长非常缓慢、基本没明显的升高，即寿命前期拟合建模的误差比较大；当滤芯压差明显增长时就进入寿命周期的中期，寿命中期压差随时间增大的规律性比较强，建立的数学模型比较接近实际情况，间接评定实际寿命的误差也就相对较小；在寿命后期压差的增长很快，用拟合模型评定的误差也会增大。

综上分析，间接评定方法比较适合于滤芯中后期寿命的评估，对滤芯前期寿命的评定没有参考价值。

3 结束语

本文针对工程机械液压过滤器实际寿命的评定方法，建立了直接评定模型和间接评定模型。该模型在满足以下条件时才能够成立，因此，过滤器实际寿命在应用评定实践时也需要满足同样条件才具有参考意义：

（1）工作和试验条件相同，即工作流量、温度与试验流量、温度（油液黏度对等）相同；

（2）试验粉尘须用ISO FTD细粉尘；

（3）被评定过滤器滤芯的过滤比β5≥100、β10≥200。

本文的研究，解决了工程机械领域液压过滤器实际寿命的科学评定，为用户制定科学合理的维护计划提供技术支持，能够有效降低液压过滤器，尤其是大型装备系统液压过滤器的维护成本。同时，本文论述的研究内容和破解思路，也为制定国际标准ISO∕AWI TR 12144 并最终颁布提供了理论依据与验证支撑。