基于差分自回归移动平均模型的医用直线加速器剂量偏移预测研究

方园

安徽省第二人民医院 （安徽合肥 230000）

时间序列为按照时间顺序获得的一系列观测值的组合。随着科学技术的不断发展，对于时间序列的研究被应用于金融、气象、农业生产等领域[1-3]。时间序列数据挖掘工作的主要任务是获取数据中蕴含的与时间相关的信息，掌握事物发展的规律。通过对时间历史数据的挖掘，我们可以预测未来一段时间可能发生的数据，并以此分析事物未来的发展趋势[4]。

在放射治疗中，医用直线加速器是不可或缺的设备，其输出剂量直接决定了患者治疗的预期效果，因此，保证输出剂量的稳定性非常重要[5]。由于医用直线加速器是一类结构复杂的高精度大型医疗设备，某些元器件的故障或老化均会导致加速器输出剂量发生突发的或缓慢的变化，因此，对加速器输出剂量的日常安全监测成了放射治疗质量保证（quality assurance，QA）工作的重点[6-7]。很多学者利用统计学处理方法开展了大量关于医用直线加速器剂量稳定性的研究，且取得了较好的研究成果，为加速器剂量稳定性的监测工作提供了参考依据[8-10]。也有学者利用时间序列分析方法对医用直线加速器质量稳定性进行了分析和预测，并证实了此方法在加速器剂量预测工作中的应用可行性[11]。鉴于此，本研究对医用直线加速器质控工作中的剂量监测数据进行了研究，并利用时间序列挖掘知识进行了数据分析，以达到对加速器剂量偏移进行预测的目的。

1 数据来源

本研究的数据来源于我院放射治疗中心医科达precise 直线加速器，选取3个调整周期内共计66条加速器剂量实测数据作为实验样本。

2 研究方法

首先，选取1个调整周期内的前19条剂量监测数据作为原始研究数据，对其进行稳定性分析；然后，利用时间序列研究中常用的差分自回归移动平均（auto regressive integrated moving average，ARIMA）模型对其进行建模并预测后5次的测量结果；最后，将预测结果与另外两个测量周期用同样预测方法得出的预测结果进行对比分析。

2.1 线性模型的建立

ARIMA 模型于1976年由Box 和Jenkins 等学者提出，之后被广泛应用于经济、金融和医疗等领域[12-14]。ARIMA（p，d，q）模型的通式为：

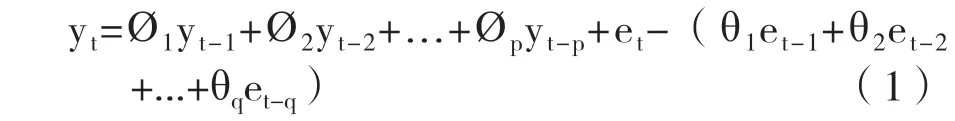
该模型分为前后两部分，前部分Ø1yt-1+Ø2yt-2+...+Øpyt-p是自回归方程，后部分et-(θ1et-1+θ2et-2+...+θqet-q）是误差移动方程，其中，yt是当前值，Ø1、Ø2...是自相关系数，θ1、θ2...是误差系数，yt-1、yt-2...及et-1、et-2...是滞后项，et是误差，p 是自回归项数，q 为移动平均项数，d 为时间序列成为平稳时所作的差分次数。

2.2 应用ARIMA 模型对数据进行分析

存在一定发展趋势的时间序列均是非平稳的，而ARIMA模型必须建立在平稳的基础上才有意义[15]。因此，时间序列建模首先应去除确定性因素，包括趋势和季节性因素，然后检测剩下数据的平稳性，最终通过检验的数据才可进行ARIMA建模，建模的具体参数可以通过残差自相关函数（autocorrelation function，ACF）和偏自相关函数（partial autocorrelation function，PACF）值来确定，R语言中有1个被命名为“auto.arima”的函数，可以用来直接定参，然后用此参数进行模型的拟合和预测[16]。

auto.arima 函数是Hyndman-Khandakar 算法的1个变种，其结合了单位根检验、最小化赤池信息准则（Akaike information criterion，AIC）和极大似然估计（maximum likelihood estimate，MLE）等评价标准来获得1个ARIMA 模型。

Hyndman-Khandakar 自动ARIMA 建模算法步骤如下：

步骤1：通过重复地进行单位根检验（Kwiatkowski Phillips Schmidt Shin test，KPSS）测试来确定差分阶数d（0≤d≤2）。

步骤2：对数据差分d 次之后，通过最小化AIC来选择最优的p，q；算法通过stepwise search 而不是遍历所有可能的p，q 组合来寻找最优的p，q 组合。

2.3 数据验证

我们通过对周期内的数据进行观察，发现其呈现逐步上升的趋势且不存在季节性因素，剂量实测数据序列见图1。

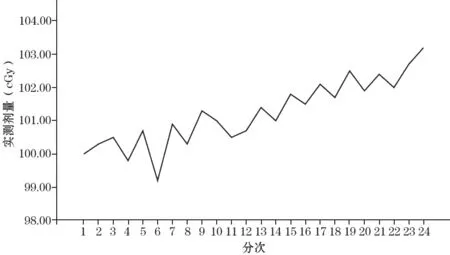
图1 剂量实测

经过一阶差分和R 语言中的auto.arima 函数，我们得到1个p，q 的最优组合，即ARIMA（1，1，0）。剂量预测模型的拟合预测见图2。

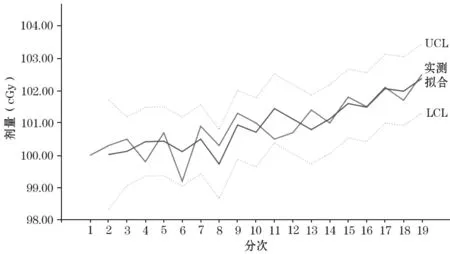
图2 剂量预测模型的拟合预测

通过对预测模型的残差ACF 和PACF 值的观察，发现取值均在置信区间内，因此残差检验可通过。预测模型的残差ACF 和PACF 值见图3；预测模型的参数估计见表1，由表可知，ARIMA（1，1，0）模型的参数在统计学上显著。

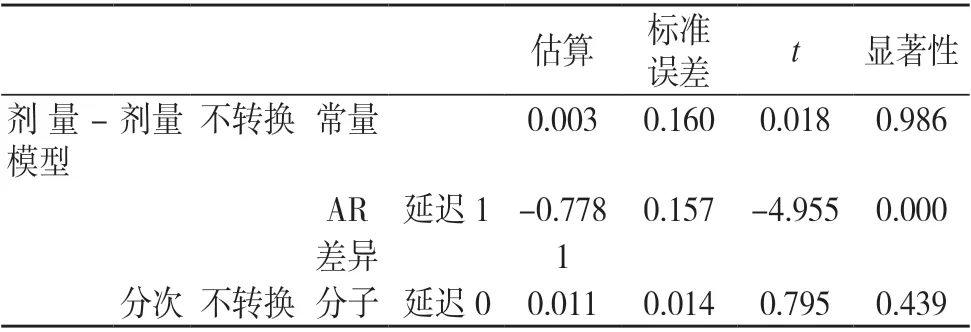
表1 ARIMA 模型的参数

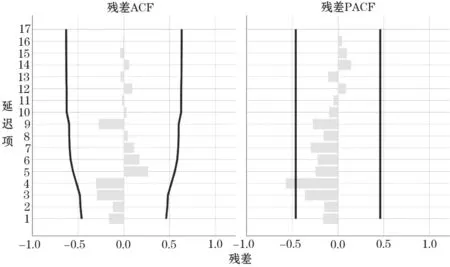
图3 预测模型的残差ACF 和PACF 值

3 结果与分析

经过ARIMA 模型参数的选取、检验和确认，发现运用此模型获得的在1个预测周期内的预测值能够较好地反映医用直线加速器剂量变化的范围和趋势，预测结果见图4和表2。表2是周期内第20～24次的剂量预测值与实测值的对比，通过对比可知，预测值对实测值有较好的体现，预测误差为0.18%～0.80%。

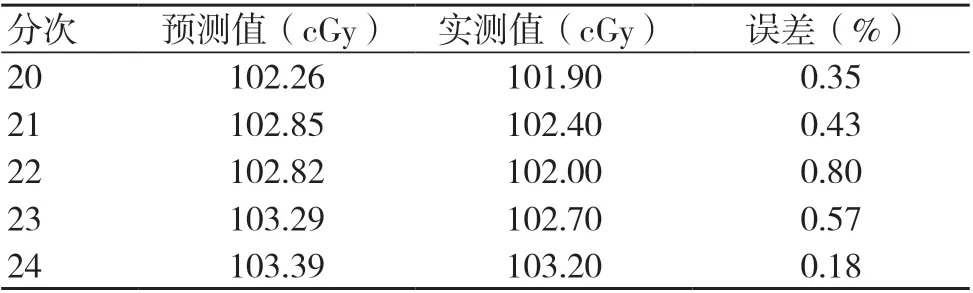
表2 剂量预测数据与实际数据的对比

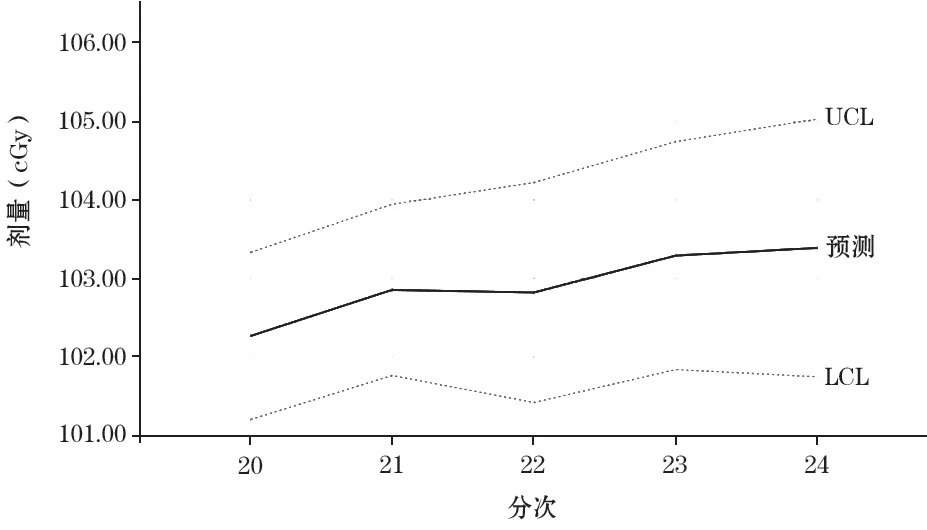
图4 剂量预测值

在对数据结果进行总结时，我们发现预测是基于1个固定周期内的数据进行的，为了明确ARIMA模型在其他周期内的数据表现，本研究就此增加了两个测量周期的数据并用上述方法进行了预测和对比，发现ARIMA（1，1，0）模型对其他测量周期的数据预测也具有较好的表现。周期二、三的预测结果见图5和表3。表3中周期二、三分别代表的是两个测量周期第20～24次的实测值和预测值，由表可知，运用此模型两组预测值与实测值的对比表现良好，误差为-1.28%～0.50%。

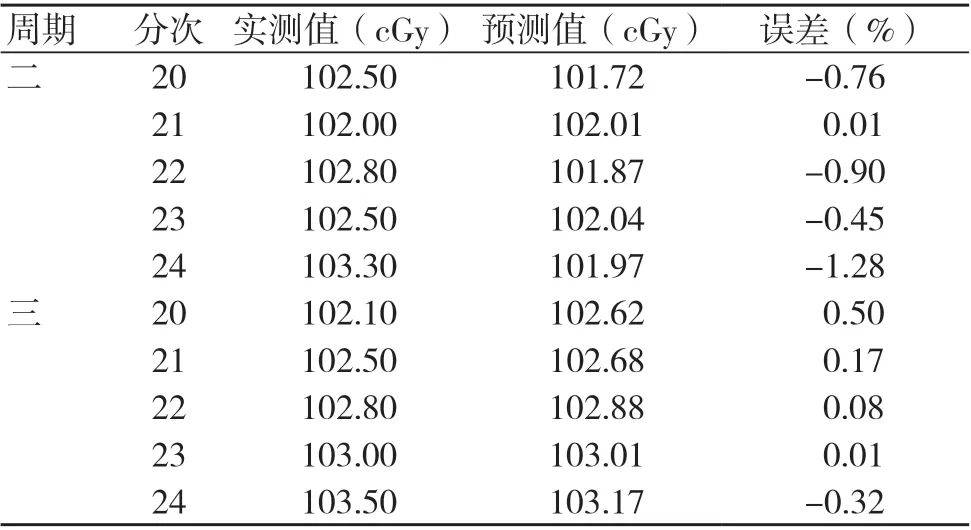
表3 周期二、三剂量预测数据与实际数据的对比

4 小结

本研究提出的利用时间序列进行医用直线加速器剂量预测方法，具有较好的预测精度，对加速器剂量参数的及时调整起到了参考和提示作用。但是，ARIMA 模型也存在一定的局限性，仅适用于正常检测和调整内的数据预测，当医用直线加速器出现维修和保养，且维修和保养的项目影响到剂量输出时，此模型将不再适用，检测周期应以维修和保养后的时间开始计算。