Volta's混沌系统自适应滑模同步
王东晓,李自强
(郑州航空工业管理学院 数学学院,河南 郑州 450046)
混沌是非线性动力系统的固有特性,是非线性系统普遍存在的现象,混沌理论所研究的是非线性动力学混沌,目的是要揭示貌似随机的现象背后可能隐藏的简单规律,以求发现一大类复杂问题普遍遵循的共同规律。混沌系统同步属于混沌控制范畴,一直是广大科研工作者兴趣所在,是研究的一个热点。
随着研究的深入,混沌系统的同步有着广泛的应用前景,同步问题备受关注,新的系统新的方法层出不穷。毛北行等[1]研究了非线性复杂网络混沌系统的有限时间同步问题;分数阶相比整数阶系统存在更普遍,研究分数阶系统同步的文献大量出现,毛北行对滑模同步两种方法进行比较[2],较早出现的自适应方法也常常用于整数阶或分数阶混沌系统同步[3,4];张燕兰采用自适应方法实现分数阶Rayleigh-Duffling-like系统的广义投影同步;滑模同步方法是我们兴趣小组常用的工具,整数阶分数阶都有实现同步[5,6],余明哲等[7]滑模自适应同步了一类不确定分数阶系统;钟启龙等[8]采用主动滑模研究了分数阶混沌系统同步问题;同样可以实现整数阶系统与分数阶系统同步问题[9];两个不同系统的同步也可以利用自适应滑模控制来实现[10]; Volta's混沌系统[11,12]在物理、通信等方面有着广泛应用,张振等[13]研究了分数阶Volta's系统同步问题;李娇研究了Volta's系统的混合投影同步[14];张志明等[15]对Volta's混沌系统添加一个新的状态变量,得到一个四维的自治超混沌系统。在上述研究的基础上,本文采用滑模控制同步方法,研究了三维整数阶和三维分数阶Volta's混沌系统同步问题,给出了系统取得同步的充分性条件,最后的数值仿真结果表明我们方案的有效性和可行性。
1 主要结果
考虑如下三阶Volta's混沌系统[11,12]
(1)
系统初始值(x1(0),x2(0),x3(0))=(1,2,8),此时系统呈现混沌态,如图1。而分数阶系统更具有实际意义,
定义1[15]分数阶Caputo导数的定义
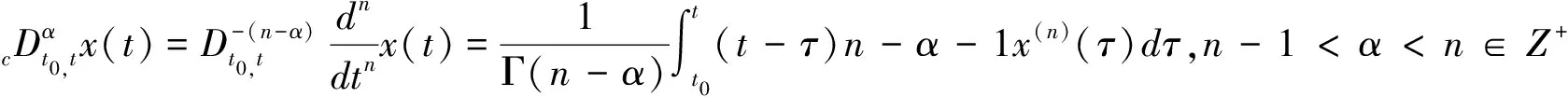
(2)
分数阶q=0.98,系统初始值(x1(0),x2(0),x3(0))=(1,2,8),吸引子如图2.
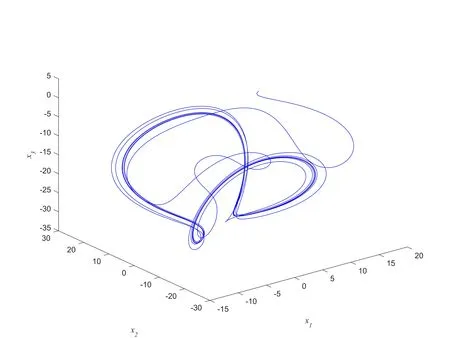
图2 分数阶Volta’s系统的混沌吸引子
下面分别用滑模控制实现两系统的同步.
以系统(1)作为驱动系统,其对应的响应系统设计为:
(3)
其中Δfi(y)为不确定项,di(t)为外部扰动,ui为控制器,取误差变量ei=yi-xi,(i=1,2,3),误差系统如下:
(4)
假设1:参数mi,ni>0,使得|Δfi(y)| 定理1构造控制方案,选取控制器: 在该方案控制下,误差系统趋于零,主从系统(1)与(3)同步. 证当状态变量在滑模面上运动时,将控制输入ui(t)代入误差系统(4),其第一个方程即为: ≤-e2 那么e2→0,同理,有第三个方程可得e3→0. 当系统状态变量不在滑模面上运动时,构造Lyapunov函数 则Lyapunov函数关于时间t的导数: ≤ 下面我们再来考虑分数阶的Volta's混沌系统同步问题,以系统(2)作为驱动系统,其对应的响应系统设计为: Dtqy1=-y1-19y2-y2y3+Δf1+d1(t)+u1 Dtqy2=-y2-11y1-y1y3+Δf2+d2(t)+u2 Dtqy3=0.73y3+y1y2+1+Δf3+d3(t)+u3 (5) 响应系统(5)减去驱动系统(2)得到误差系统: Dtqe1=-e1-19e2-(y2y3-x2x3)+Δf1+d1(t)+u1 Dtqe2=-e2-11e1-(y1y3-x1x3)+Δf2+d2(t)+u2 Dtqe3=0.73e3+(y1y2-x1x2)+Δf3+d3(t)+u3 (6) 引理2[17]若x(t)为连续可微的函数,则有∀t≥t0 阅读前的调查显示青少年会花精力去查找他们要读什么。主要有三方面行为的调查:目标锁定行为的调查结果显示,大部分青少年都有自己非常喜欢的书籍类型,已经形成自己的阅读内容偏好,并将这种偏好作为自己锁定阅读目标的重要考虑因素;阅读决策行为的调查结果显示,65%的被调查者认为参考他人、查找评论、试读、书籍比较是其普遍选择,同时,查找网络评价、网上试读两个选项的调查结果差异较大;书籍获取行为的调查结果显示,68%的被调查者使用手机、iPad等移动设备进行阅读,65%的被调查者通过搜索引擎查找想读的书籍。 定理2构造控制方案,选取控制器: 在该方案控制下,响应系统(5)与驱动系统(2)同步. 证当状态变量在滑模面上运动时,将控制输入ui(t)代入误差系统(6),其第一个方程即为: 在滑模面上s=0及假设1条件下,所以Dtqe1≤-e1,那么e1→0.第二个方程: ≤-e2 那么e2→0,同理,有第三个方程可得e3→0. 当系统状态变量不在滑模面上运动时,构造Lyapunov函数 则Lyapunov函数关于时间t求q阶分数阶导数: ≤ 图3 定理1的系统误差曲线 图4 定理2的系统误差曲线 研究了Volta's混沌系统的同步控制问题,分别对三维和四维混沌系统设计了控制方案,得到了整数阶Volta's混沌系统同步的充分性条件,给出了严格的数学证明和推理过程,数值仿真表明该方法有效性和可行性。
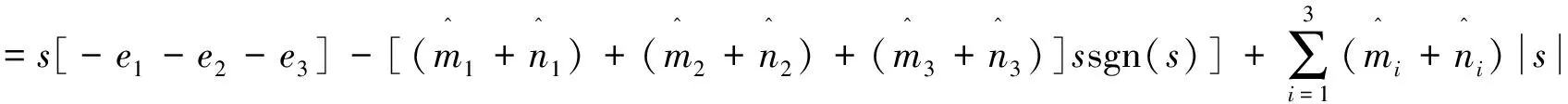

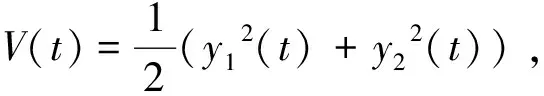

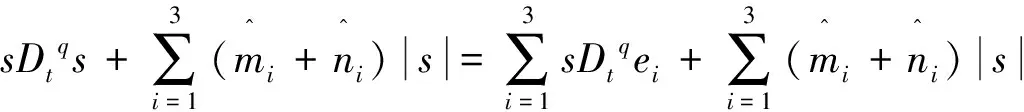
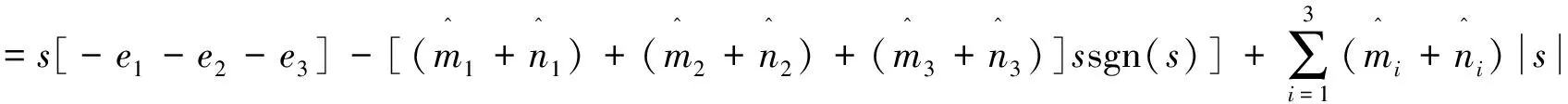
2 数值仿真
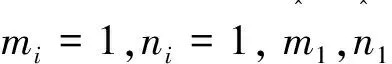


3 结论

