基于Wiener过程的风电机组轴承剩余寿命预测

彭 鹏，马世明，慕 松

(1.宁夏龙源新能源有限公司，银川 750000；2.宁夏新能源研究院(有限公司)，银川 750000；3.宁夏大学机械工程学院，银川 750000)

0 引 言

轴承是风电机组传动部分至关重要的部件之一，其运行状态的好坏及其寿命直接影响着风电机组的运行状态。目前，在风电机组轴承的剩余寿命预测方面，国内外的研究相对较少[1]。相关研究所采用的特征数据多为载荷或振动信号[2-5]，但这两种信号的采集需额外增加信号采集系统，增大运维成本；通过有限元分析方法进行模拟仿真[5-7]，或在参考标准轴承寿命计算公式的基础上运用修正公式进行计算[8-9]，由于没有充分考虑轴承所受的环境影响，难以有效应用于实际的运维检修中；建立基于神经网络的轴承寿命预测模型[10-11]需要提取大量的训练样本，在实际应用中也难以实现。胡姚刚等人提出了基于温度的实时寿命预测方法[12]，该方法忽略了轴承温度变化相对与转速变化的滞后性，因此并不能有效的应用于实际运维检修中。

本文提出基于Wiener过程的风电机组轴承寿命预测方法。首先，以时间、风电机组转速和轴承温度为特征量，建立轴承温度、转速及时间之间的多元线性关系模型；其次，根据建立的关系模型设立新的轴承运行状况监测方案；再次，建立轴承性能退化模型，根据以退化参数首次超过失效阈值判定轴承失效原则，建立基于Wiener过程的轴承寿命预测模型；最后，以实际运行风电机组的齿轮箱轴承性能退化数据为例，对本文提出的方法进行验证。

1 风电机组轴承特征量关系模型与运行状况监测

1.1 轴承特征量提取与关系模型建立

风电机组轴承温度和转速、摩擦扭矩等多种因素有关，其中SCADA系统直接记录的参数为转速，而因为热量由轴承内圈传到温度传感器有延时，因此有必要建立轴承温度、转速和时间三者之间的关系模型。从SCADA数据中建立轴承实时温度、时间以及转速之间的关系模型，本文按时间序列从SCADA系统提取各特征参量数据(t0,T0,r0)、(t1,T1,r1)、…、(tn,Tn,rn)，其中，t0、t1、…、tn为SCADA系统中直接导出的连续时间点，时间间隔为数据采集周期T。根据文献[13-14]可得出风电机组轴承的总生热量和转速成正比，并且轴承的温度场为由内到外逐渐递减的，在传递过程中有一定热量损失，其测量温度值可视为多个连续时间点共同作用的结果，因此，轴承实际测量温度可用下面函数表达式表示：

(1)

式中，Tt为t时刻的轴承测量温度；a为相对转速温升系数；αi为t-τ-iT时刻温升量相对于在t时刻温升量所占的权重；rt-τ-iT为第(t-τ-iT)时刻的转速；τ为测量滞后时间(热量从轴承传感器部位的时间，不满一个数据采集周期按一个采集周期算)；T为数据采集周期；T0为初始温度；εt为偏差。

式(1)中的τ值表征轴承自身材料的热传导性能；n值为某时刻轴承上的生热量在轴承上的保持时间所占的采集时间的个数，表征轴承的传热性能；a值表征轴承的生热性能。式中τ值和n值可通过观察各转速和温度转折点的时间差或进行仿真确定，其他参数可通过运用最小二乘法然后进行数据归一化处理确定。

1.2 运行状态监测及退化趋势量提取

风电机组轴承的运行状况监测是通过监测轴承的温度来实现的，其预警保护一般是设置温度上限作为报警、故障阈值。但实际上，由于风速的随机性而使风电机组转速也具有一定随机性，当其没有在最大转速下运行时，单纯的温度值并不能及时有效的对轴承的运行有效的监测和对故障的及时报警。本文提出一种新的状态监测以及报警阈值设定方法，根据风电机组正常运行参数，确定式(1)中的各参数，然后将风电机组的实时运行参数代入已确定的关系式中，可得t时刻相对转速温升系数(即t时刻的性能退化趋势量)at值为：

(2)

将风电机组在额定最大转速下以及额定温度阈值代入(2)式中，即可得到at的阈值ζ，通过t时刻相对转速温升系数at值大小判断判断轴承的实时运行状况，at值越小，则轴承运行状况越良好；反之，at值越大，则表明轴承运行状况越差；当at值大于所设阈值ζ时则发出报警。为消除时间序列中的随机变动，根据文献[12]，本文采用移动平均法对所得退化趋势量进行滤波。

2 风电轴承的剩余寿命预测模型

2.1 风电轴承性能退化模型建立

按时间序列从SCADA系统提取各特征参量数据(t0,T0,r0)、(t1,T1,r1)、…、(tn,Tn,rn)，通过式(2)计算可得出风电轴承相对转速温升系数的趋势量序列为(t0,a0),(t1,a1),…,(tn,an)，由于轴承在各个运行阶段受到的外界不良因素的影响程度不同，随着轴承的劣化不断加重，轴承的相对转速温升系数a将是波动上升的。因此，根据文献[15-17]，本文采用分别运用线性Wiener过程和非线性Wiener过程对其进行建模。风电轴承在时刻t的性能退化趋势量xt的表达式为：

xt=x0+μtr+σB(t)

(3)

式中，x0为退化趋势量初值；μ为漂移参数；B(t)为标准的Wiener过程；σ为扩散参数；r为t的指数。当r不为1时，此过程为非线性Wiener过程；当r为1时，此过程为线性Wiener过程。

2.2 性能退化参数估计

(4)

式中，Δxi=xi-xi-1；σΔB(ti)=σΔB(ti)-σΔB(ti-1)，由Wiener过程定义可知ΔB(ti)～N(0,Δti)，因而可得：

(5)

由Wiener过程的定义可知，Δx1,Δx2,…,Δxn满足独立同分布，即样本似然函数为：

L(μ,σ,r)=f(Δx1)f(Δx2)…f(Δxn)

(6)

根据式(5)和式(6)进一步可得样本的对数似然函数为：

(7)

式(7)对μ和σ求偏微分并令其等于0：

(8)

(9)

求解式(8)和式(9)构成的方程组可得μ和σ的极大似然估计值分别为：

(10)

(11)

将式(10)和式(11)代入式(7)，可得关于r的轮廓似然函数(除去其中常数项)为：

(12)

2.3 风电轴承剩余寿命预测模型

一般认为轴承性能失效都是在性能特征量首次超过失效阈值时，因此可定义退化参数x值首次超过所设阈值ζ即认为失效[17]。风电轴承剩余寿命Lt是指轴承从当前时刻t时的性能退化量到其第一次超过失效阈值的时间。即Lt可表示为：

Lt=inf{xt≥ζ}={t|xt≥ζ,xs
≤ζ,0≤s≤t}

(13)

根据文献[18]，利用下式逼近Lt的概率密度函数：

(14)

根据概率密度函数可知，f(ti)可以认为是在时间点ti附近极小范围内可能达到失效阈值ζ的概率，因此，本文将概率密度函数的最大值f(t′)对应的时间点t′作为轴承的剩余寿命Lt，预测流程如图1所示。

图1 风电轴承剩余寿命预测流程图

为了表征预测结果的差异程度，采用相对误差进行表示：

(15)

式中，e为轴承的寿命预测相对误差；L为轴承的实际剩余寿命。

本文提出的风电机组轴承剩余寿命预测模型，可对风电机组轴承的剩余寿命进行实时预测。在剩余寿命预测中，预测剩余寿命概率分布与检测数据量N有密切关系，根据文献[12]，N≥2 000即可满足统计分析要求。

3 实例分析

3.1 实例说明

为了验证本文方法的有效性及可行性，以某风场1 WM风电机组的齿轮箱轴承温度作为特征量为例进行验证，由于此型号风电机组齿轮箱的结构及测点布置(如图2所示)原因，此温度值所表征出来的为轴承和制动器二者的共同退化特征。

图2 温度传感器测点布置示意图

由于温度值受到制动器的影响，当转速达到上限值保持基本恒定时，温度的变化与风速成正相关，而当转速未达到上限值时，风速大小和转速大小成正相关关系，即温度的变化与风速成正相关，因此本文实例部分用风速代替文中提出的转速进行验证。此测点温度值自2018年1月6日齿轮箱维修后(一般认为刚检修后为正常状态)在2018年7月21日15时53分超出阈值95 ℃发生报警。本文提取从一月份维修后到七月份报警之间的温度及风速数据，数据采集时间间隔为8 min，如图3所示。

图3 风速及齿轮箱轴承温度监测数据

由图可见，此温度值随风速变化而波动，直到报警前温度的整体趋势是上升的。实例将以图3所示的数据为基础，根据文献[19]对数据中的异常数据进行清洗，并取其相邻时间点的数据平均值进行填充。以图1中的流程对此测点进行寿命预测，并进行对比验证分析。

3.2 齿轮箱轴承温度的剩余寿命预测与对比分析

运用1月份维修后的5000组数据对式(1)模型进行训练，训练后所得到的式(1)中相对转速温升系数a为2.949；4个时刻温升量相对于在时刻温升量所占的权重分别为0.384、0.177、0.185、0.254；初始温度T0为38.516 ℃。

进而根据公式(2)并运用移动平均法进行滤波得性能退化趋势量时间序列如图4所示。

图4 齿轮箱轴承性能退化趋势量

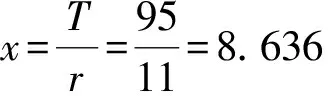
按时间序列提取以每5000组数为一个周期共5组数组，通过式(11)、(12)、(13)的计算，分别得到非线性Wiener过程和线性Wiener过程各周期的性能参数见表2-表3。

表2 非线性Wiener过程各周期性能参数

表3 线性Wiener过程各周期性能参数

根据表2、表3中各参数，运用式(14)计算出各周期的概率分布如图5所示。

图5 齿轮箱轴承剩余寿命预测结果的比较

图5所得的非线性Wiener过程和线性Wiener过程预测结果及相对误差分别见表4-表5所示。

表4 实际剩余寿命与非线性Wiener过程预测剩余寿命的对比

表5 实际剩余寿命与线性Wiener过程预测剩余寿命的对比

由上表4、表5可以看出，不论非线性Wiener过程还是线性Wiener过程，除了非线性Wiener过程在第5周期和线性Wiener过程在第3周期的预测结果偏差过大外，其他各个监测周期的预测误差天数以及相对误差随着运行时间的推移总体呈减小趋势。除了第3周期和第5周期，其他三个周期运用非线性Wiener过程和线性Wiener过程的预测结果相差不大，因此在实际应用中为了简化计算，可采用线性Wiener过程为主方法进行寿命预测，按照时间序列其预测结果应呈波动减小趋势，当出现局部预测结果与主趋势偏差较大时，可运用非线性Wiener过程作为辅助对局部预测结果进行校正。

4 结束语

(1)建立了风电轴承温度、转速以及时间之间的关系模型。

(2)提出了一种新的轴承运行状态实时监测方法。

(3)分别运用非线性Wiener过程和线性Wiener过程建立了风电机组轴承性能退化模型及剩余寿命预测模型。

(4)以实例对上述方法进行了验证，并对其结果进行了对比分析。