基于比面积调控的潜水排污泵内部流动特性

陈建华，周岭，张帆，房鑫，黎义斌*

(1.江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013；2.兰州理工大学能源与动力工程学院，甘肃 兰州 730050)

潜水排污泵是输送工业生产废水、城市生活污水等固液两相流的重要设备，在化工、冶金、采矿以及城市排污、防洪排涝等领域应用广泛[1-3].潜水排污泵属于离心泵的一种.目前，国内污水处理厂采用的潜水排污泵存在较多问题，如易堵塞、噪声大、寿命短等，对污水处理厂运行稳定性及其产能达标造成不利影响，因此对潜水排污泵的运行稳定性和效率提出了更高的要求.而叶轮与蜗壳匹配不当，以及隔舌和叶轮的动静干涉效应是导致潜水排污泵产生噪声和压力脉动的主要原因[4-6]，对泵内部流动特性，特别是噪声和压力脉动产生机理进行研究具有重要意义.

在改善泵运行稳定性及提高效率方面，许多学者主要针对叶轮进行优化设计，提出了多种方法，如设置产生预旋的前置导叶、斜切叶轮出口边、减少叶片数、选取较小的叶片出口角和叶轮出口宽度、设计变螺距诱导轮和复合叶轮等[7-9].而蜗壳也是离心泵重要的过流部件，其水力性能对泵整体性能有较大影响，有研究表明，蜗壳中的水力损失占离心泵整体水力损失的将近一半[10].因此，应把叶轮和蜗壳这两大水力部件联系在一起进行设计，选取合适的比面积，使叶轮和泵体更具有良好的匹配性.ANDERSON[11]首次提出了离心泵的比面积原理，指出叶轮出口过流面积与泵体喉部面积之比是影响泵扬程、流量和轴功率等特性的主要决定因素，并给出了扬程系数、流量系数和比转数与比面积的关系曲线.赵万勇等[12]针对某泵站S700-500-730 型双吸离心泵运行时引发的断轴问题，采用CFD 数值模拟方法，分析了不同的蜗壳断面面积变化规律对泵水力性能及叶轮径向力的影响.BELBACHIR等[13]通过对比基础设计与附加设计的3种蜗壳，分析了三者的水力特性、叶轮周向速度分布以及压力分布，表明蜗壳设计对泵的水力性能影响显著.刘厚林等[14]采用CFD数值模拟方法研究了5种不同的蜗壳断面面积变化对离心泵性能的影响规律，认为拥有良好水力性能的蜗壳应符合螺旋段尾部面积增长较慢、螺旋段前半段面积适当增大的规律.

综上，目前就比面积调控对离心泵水力性能影响的研究还比较少，且不够全面，尤其比面积调控对潜水排污泵水力性能影响的研究鲜见文献报道.潜水排污泵叶轮与蜗壳参数匹配对提高泵机组水力性能和运行稳定性至关重要，比面积是影响泵水力效率的关键变量.因此，文中以某一比转数ns=261的潜水排污泵为研究对象，设计3种不同比面积调控方案，分别进行数值计算，对比分析不同比面积调控方案对潜水泵水力性能的影响规律，并进行试验验证，为提高潜水排污泵的优化设计提供一定的参考.

1 计算模型及数值计算方法

1.1 计算模型

以某型比转数ns=261的潜水排污泵为研究对象,该泵主要设计性能参数分别为流量Qd=750 m3/h，扬程H=20.59 m，转速n=1 480 r/min；主要设计几何参数分别为叶轮进口直径D1=240 mm，叶轮出口直径D2=315 mm，叶片进口安放角β1=11°，叶片出口安放角β2=23°，叶片出口宽度b2=98 mm，叶片数Z=4，蜗壳基圆直径D3=350 mm，蜗壳出口宽度b3=140 mm，蜗壳出口直径Dd=300 mm，比面积Y=1.218.图1为潜水排污泵的叶轮和蜗壳轴面图及其计算域图，图中b2为叶片出口宽度，Φ为蜗壳隔舌安放角.

图1 潜水排污泵叶轮和蜗壳轴面图

潜水排污泵计算域模型如图2所示，主要包括泵进口段、叶轮、蜗壳、出口段等.

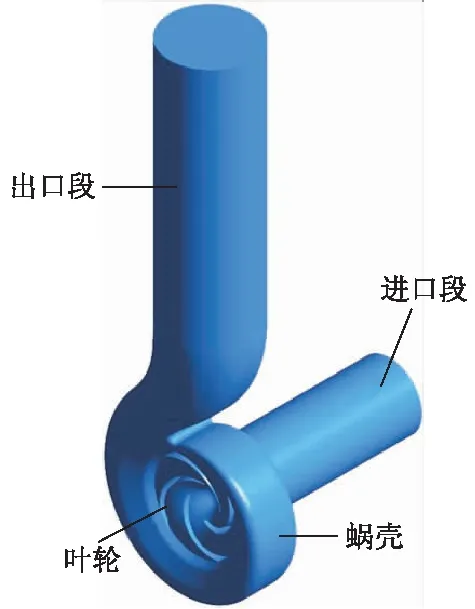
图2 计算域模型

根据Anderson比面积原理[11]，可以通过改变叶轮出口和蜗壳进口结构几何参数来调控比面积大小.定义比面积Y为

(1)

式中：F1为叶轮出口面积，通常由叶轮出口直径D2、叶片出口宽度b2和叶片出口安放角β2决定；F2为蜗壳隔舌处断面面积，由于隔舌处断面难以测量，通常以蜗壳第Ⅷ断面面积替代.

研究表明，潜水排污泵比面积和隔舌安放角的变化会同时影响蜗壳的水力性能.但当隔舌安放角在0°～5°以内变化时，比面积的变化成为影响蜗壳效率的主要因素，此时蜗壳整体性能较佳.在设计蜗壳时，优先考虑比面积的取值，尽量保证比面积接近1，然后隔舌安放角在参考值附近变化.当比面积增大(或减小)，且隔舌安放角减小(或增大)时，可以保证潜水排污泵的效率维持不变.比面积的大小与隔舌安放角有关，由此根据不同的隔舌安放角度，设置3种比面积调控方案，如表1所示.

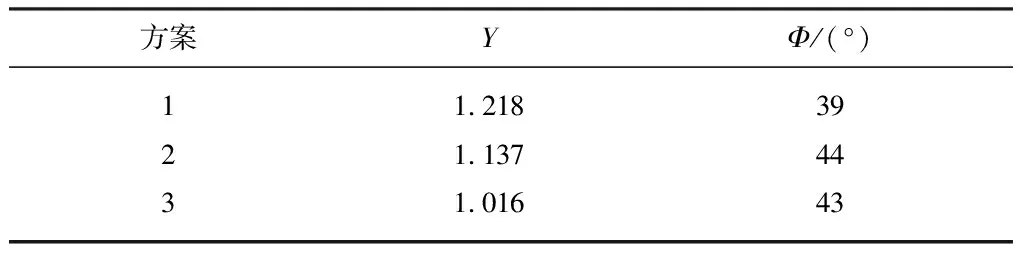
表1 3种比面积调控方案

1.2 网格划分及无关性验证

对计算域模型进行网格划分，均采用非结构化网格.考虑到网格数量对数值计算结果的影响，方案1蜗壳采用四面体网格，泵进口、出口和叶轮采用六面体网格进行划分；方案2和方案3所有计算域采用六面体网格划分.由于叶片进口及出口处流动较复杂，且速度梯度变化很大，因此对该区域网格进行加密，其他区域网格密度不变.

为了提高计算精度以及保证计算结果的准确性，以扬程为评价指标，对计算域网格进行无关性验证，如图3所示.可以看出，当计算域总网格数N为150万左右时，计算扬程趋于稳定，此后再增加网格数量，扬程变化不大.最终确定各过流部件的计算网格数分别为进口段190 485，叶轮420 867，蜗壳607 764，出口段464 535，计算域模型总网格数为1 683 651.

图3 网格无关性验证

1.3 数值计算方法

潜水排污泵的内部为三维不可压缩湍流流动，应用计算流体动力学软件ANSYS-CFX对泵内部进行定常数值计算，采用相对坐标系下的雷诺时均N-S方程描述流体的运动规律.选择RNGk-ε湍流模型和SIMPLEC算法[14-15]，采用二阶迎风格式离散基本方程,设置计算收敛精度为10-5.压力边界条件设置泵进口为速度进口，出口为自由出流，近壁区采用标准壁面函数，介质为常温清水.

2 计算结果及分析

在设计工况下，对泵内部流场进行数值计算，图4为数值计算得到的3种比面积调控方案下潜水排污泵内部流体流动速度分布云图.可以看出，相比方案1，方案2和方案3的速度分布更加贴合叶片几何形状，在叶轮流道内部，方案2和方案3的速度梯度分布更加均匀，尤其在靠近叶轮出口位置.随着蜗壳过流断面面积增大，蜗壳内部流体流动速度减缓，蜗壳与叶轮的动静干涉效应减弱.在叶轮与蜗壳的交界面，方案1和方案2有较为明显的二次流，而方案3中几乎看不到二次流.

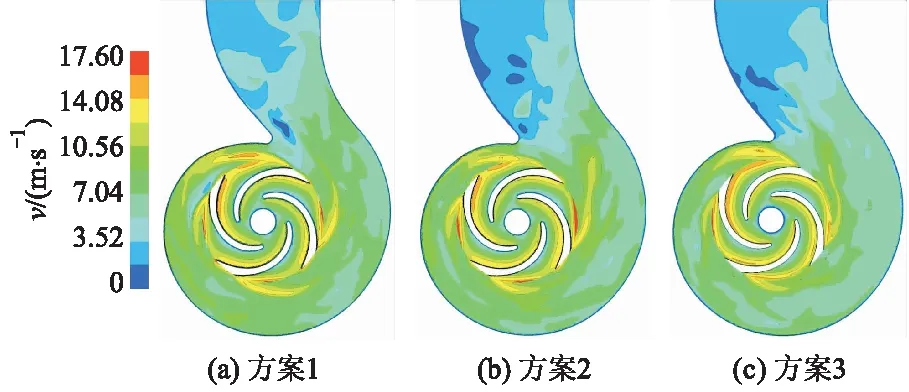
图4 3种方案的速度云图对比

图5为3种比面积调控方案下叶轮和蜗壳内部湍动能k分布，可以看出，在方案2中，仅在叶轮与蜗壳交界处湍动能略微偏大，其余位置湍动能均小于方案1和方案3.方案1和方案3中由蜗壳隔舌造成的湍动能相比方案2小，这减小了在蜗壳扩散段的水力损失，提高了潜水排污泵的效率.方案2的隔舌对蜗壳内流体扩散造成了一定的拥堵，导致蜗壳内流体能量损失，从而降低了潜水排污泵的效率.

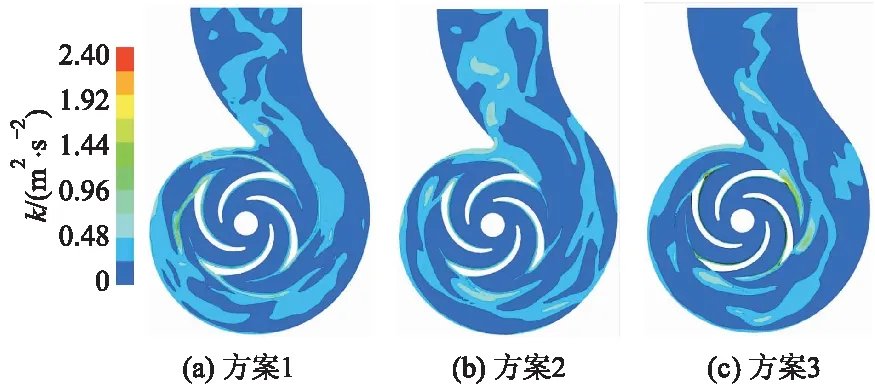
图5 3种方案的湍动能云图对比

图6为3种比面积调控方案下蜗壳内部湍动能耗散率ε分布，可以看出，在蜗壳隔舌处，方案2和方案3要比方案1的湍动能耗散率小很多.在蜗壳内，方案2和方案3流体动能转换为压能小于方案1，相对提高了蜗壳的水力效率.

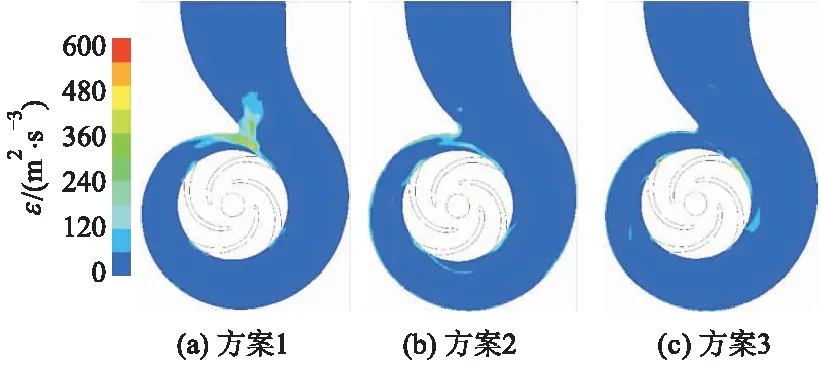
图6 3种方案的湍动能耗散率云图对比

为了更进一步地分析蜗壳对叶轮内部流动的影响，将叶轮从半径R=67.5 mm到R=157.5 mm以间隔ΔR=10 mm划分9个子区域，并以叶轮外径原点为极点，以叶片任一进口为极轴，逆时针方向为正建立极坐标系，其中变量α为极角，如图7所示.图中红色、绿色和蓝色曲线分别表示半径为77.5，107.5和137.5 mm的圆弧，选取这3个半径圆弧进行各点速度的比较.

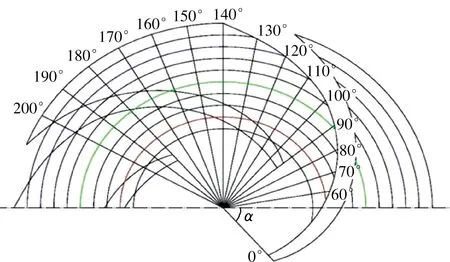
图7 叶轮流道划分示意图

图8为3种比面积调控方案下叶轮内不同半径及不同角度处的速度对比，可以看出，叶轮流道内流体的速度从叶片工作面到背面呈增大趋势.在叶轮半径R=77.5 mm的每个监测点处，方案1的速度变化比方案2和方案3更为平缓，尤其是在叶片背面附近.在叶轮半径R=107.5 mm和R=137.5 mm的每个监测点处，方案2和方案3比方案1速度分布更均匀，这表明蜗壳断面面积的变化对叶轮出口的流动有很大的影响.

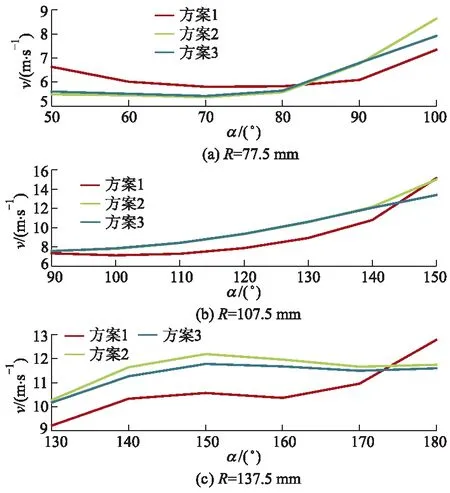
图8 3种方案的叶轮流道不同半径处速度分布

为了衡量不同工况下蜗壳将流体动能转换为压能的能力，定义量纲为一的压力系数Cp，即

(2)

(3)

式中：p2为蜗壳进口静压；pav为蜗壳每个断面的平均静压；u2为叶轮出口的圆周速度.

图9为3种比面积调控方案下蜗壳内部不同断面处湍动能和压力系数的变化对比，可以看出，方案2和方案3各断面湍动能接近，而方案1蜗壳流道内部湍动能的增长大于方案2和方案3.湍动能的增大说明蜗壳内流体的湍流强度不断增强，即不利于蜗壳将流体动能转化为压能，水力损失增大，从而降低了蜗壳的水力效率.由静压图可知，在第Ⅰ断面，3种方案的压力基本一致，但在第Ⅷ断面3种方案的压力相差较明显.方案2和方案3比方案1分别提高4.47%和2.23%.与方案2相比，方案3内部压力的增长更平稳且流动更好，使得方案3的效率高于方案2.

图9 3种方案的蜗壳各断面的湍动能及静压对比

为了衡量不同工况下蜗壳的效率，定义蜗壳水力损失κ为

(4)

式中：p3为叶轮出口总压；pout为蜗壳出口总压.

图10为不同工况下3种比面积调控方案的蜗壳水力损失对比，可以看出，3种方案的蜗壳水力损失趋势相同，都随着流量的增大而增大.在小流量工况下，方案2蜗壳内的水力损失大于方案3，而在大流量工况下则相反.在设计工况下，相比方案1，方案2和方案3蜗壳内的水力损失小约0.50%和0.38%，这表明方案2和方案3的水力性能优于方案1的.

图10 3种方案的蜗壳水力损失对比

3 试验验证

为了验证数值计算结果的正确性，在原型泵基础上根据3种不同比面积调控方案加工制造模型泵进行试验.试验在设计工况下进行，原型泵和3种方案模型泵的各性能指标如表2所示.可以看出，相比方案1，方案2和方案3的效率η有所提高，分别提高了1.75%和2.14%.方案2和方案3的泵扬程均符合设计要求.方案3的泵扬程减小，并且轴功率P也有所降低，但效率略有提升.

表2 原型泵及3种比面积调控模型泵性能对比

不同工况下，3种比面积调控方案和原始模型测试的泵外特性曲线如图11所示，可以看出，在小流量工况下，相比方案1，方案2和3的泵扬程几乎不变；在大流量工况下，泵扬程的增大并不明显，由于蜗壳并不做功，影响潜水排污泵扬程的主要因素是叶轮，在3种比面积调控方案中，叶轮完全一样，因此对扬程的影响不大；方案2的泵扬程、轴功率和效率都增大；方案3的泵扬程增大没有方案2增大得明显，且方案3轴功率增长幅度不大，因此效率的提升反而要比方案2高，最终蜗壳效率得到了提高，此时蜗壳的最佳隔舌安放角为42°～44°，而比面积为1.0～1.2.在进行蜗壳设计时，隔舌安放角和比面积在这个范围内取值，潜水排污泵的效率基本保持不变.

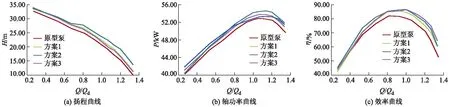
图11 原型泵及3种比面积调控模型泵的特性曲线对比

4 结 论

以某一比转数ns=261的潜水排污泵为研究对象，对其蜗壳内部流动进行分析，得到如下结论：

1)潜水排污泵比面积和隔舌安放角参数的变化会同时影响蜗壳的水力性能.但当隔舌安放角在5°以内变化时，比面积的变化成为影响蜗壳效率的主要因素.因此，在设计蜗壳时，应优先考虑蜗壳比面积的取值，尽量保证蜗壳比面积接近1，然后隔舌安放角在参考值附近变化.可以发现，当比面积的值增大(或减小)，隔舌安放角减小(或增大)时，可以保证潜水排污泵的效率维持不变.

2)通过CFD数值模拟以及试验验证，结果表明，在设计工况点，方案2和方案3的效率相对方案1有所提高.方案2提高了1.75%，方案3提高了2.14%，且方案2和方案3的泵扬程均符合设计要求.

3)考虑比面积对潜水排污泵叶轮和蜗壳流态的影响，保证叶轮不变，基于比面积调控对蜗壳水力参数进行分析，最终得到隔舌安放角在42°～44°、比面积在1.0～1.2变化时，潜水排污泵的效率基本保持不变.