可变速抽蓄机组运行转速对甩负荷过渡过程的影响

张文科，张健，俞晓东，陈胜

(河海大学水利水电学院，江苏 南京 210098)

抽水蓄能电站在运行过程中会出现不同的工作水头，而对于不同水头，发电最佳效率对应的转速不同[1].可变速抽水蓄能机组可以通过交流励磁系统改变转子励磁电压频率，从而实现变速恒频运行[2-3].相较于恒速抽水蓄能机组，可变速抽水蓄能机组具有更高的运行效率[4-5].

目前，国内外对于可变速抽水蓄能机组的研究主要集中在变速机组水力、机械、电气系统的模型建立、变流器励磁控制和机组的优化运行.BORTONI等[6]在实验室中进行了电站变速运行的理论分析和试验，阐述了电站变速运行的益处和经济可行性.KUMARI[7]提出了一种互补滑模控制器(CSMC)，并与传统的PID控制器进行了分析比较，仿真结果表明了该控制器在控制过程中的有效性.BORKOWSKI等[8]提出了小型水电站(SHP)的变速操作和不同的控制技术.GAO等[9]研究了一种变流器供电的同步发电机能够在全工况下进行变速操作(VSO)的系统.柳海生等[10]提出了一种基于最小二乘法曲面拟合抽水蓄能电站水泵水轮机效率的计算方法，建立了水泵水轮机效率拟合模型，得到拟合结果.乔照威等[11]阐述了可变速抽水蓄能机组水泵工况起动方式研究概况与发展现状，在此基础上重点分析了异步起动与定子短接起动2种起动方式.张宝勇等[12]介绍了变转速水泵水轮机机组容量、转速变化范围等主要参数的选择方法，以及变转速与定转速水泵水轮机运行范围、稳定性等主要参数选择的异同.蔡卫江等[13]提出了一种从模型综合特性曲线入手，以效率优化为目标的转速及开度寻优策略.陈秋华等[14]分析了水泵水轮机从2个不同初始运行工况发生飞逸过程时水力特性的差别，相对于流动条件较好的额定工况，由流动条件较差的部分负荷工况开始的飞逸过程更容易引起水泵水轮机运行轨迹的剧烈跳动以及流道压力脉动.周喜军等[15]研究了可变速机组在事故甩负荷工况下的转速上升规律.可见，针对可变速抽水蓄能机组水力侧过渡过程研究相对较少，不同的运行转速对机组甩负荷过渡过程的影响及其机理还需深入研究.

文中在前人的研究基础上，通过建立可变转速抽蓄电站初始运行转速计算及过渡过程仿真模型，研究不同水头工况下的甩负荷过渡过程，分析不同初始转速对机组最大转速上升率及水锤升压的影响，以期为变转速抽水蓄能电站的过渡过程仿真及控制提供参考.

1 计算模型

1.1 有压管段瞬变流模型

有压管道瞬变流的运动方程和连续方程分别为

(1)

(2)

式中：H为测压管水头；v为管道中的流速；f为摩阻系数；D为管道直径；θ为管轴线和水平面的夹角；a为水锤波速.

式(1)，(2)可简化为标准的双曲型偏微分方程，从而利用特征线法转化为同解的管道水击计算特征相容方程，特征线方程可表示为

C+:HPi=CP-BPQPi,

(3)

C-:HPi=CM+BMQPi,

(4)

式中:HPi,QPi分别为断面i的压力水头、流量;CP,CM,BP，BM为特征方程系数，均为t-Δt时刻的已知量.

1.2 水轮机模型

水轮机节点的控制方程包含水头平衡方程以及转动力矩平衡方程.将特征线方程代入水头平衡方程可得转轮边界水头平衡方程[16]，即

h=(CP1-CM2)/Hr-q(BP1+BM2)Qr/Hr,

(5)

(6)

式中：下标0代表上一时刻计算值，下标1，2代表转轮上、下边界节点编号；Hr，Qr分别为额定工况转轮工作水头和流量；Nt为机组转速上升值,是量纲为一的参数；Δt为时间步长；Ta为机组惯性时间常数；δt0，δt0-Δt为机组转动阻力矩，是量纲为一的参数.

此外，在可变速抽水蓄能机组事故甩负荷时，双馈感应电机脱网，故甩负荷过渡过程计算中不考虑电气侧交流励磁等电气系统对水力侧水泵水轮机产生的影响.

2 算例分析

2.1 工程概况

以某拟建的可变转速抽水蓄能电站为例.电站装设4台单机容量250 MW的混流可逆式水泵水轮机组，转轮直径为4.5 m，总装机容量为1 000 MW.电站发电最大水头414 m、最小水头363 m，额定水头379 m，额定发电流量76.2 m3/s.输水线路布置于上、下库之间山体内，洞线采用直线布置，发电厂房采用中部式方案；引水及尾水系统分2个水力单元，均采用2洞4机布置，计算时选取其中1个水力单元，即一洞两机的布置形式.表1为电站基本参数，表中Hu1，Hu2，Hu3分别为上库校核洪水位、上库正常蓄水位、上库死水位；Hd1，Hd2，Hd3分别为下库校核洪水位、下库正常蓄水位、下库死水位；ne为机组额定转速；Pe为机组额定出力；J为机组转动惯量.

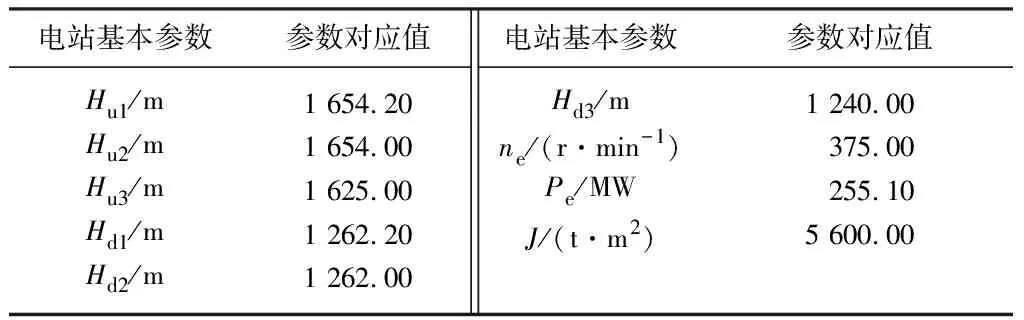
表1 电站基本参数

各调保参数控制标准：① 蜗壳最大压力值小于588 m；② 机组最大转速上升率小于45%；③ 尾水管进口最大真空保证值为3.8 m.

2.2 初始转速对发电效率的影响

选取最大发电水头、额定水头和最小发电水头作为计算比较水头，最大发电水头和额定水头条件下给定额定出力255.1 MW运行.最小发电水头试算出最大出力为190 MW.

由于励磁系统发热的限制，可变速机组转速可以在额定转速ne±10%范围内连续可调.上述工程中，额定转速为375.00 r/min，因此选取转速的可调节范围为337.50～412.50 r/min.可变速机组在发电水头变化时调整机组运行转速不仅应考虑发电效率，还应兼顾其他性能，本节仅从效率优化的角度考虑不同发电水头下的转速选取.

机组总发电效率公式为

η=P/9.81QΔH,

(7)

式中：η为总发电效率；P为出力，P=Mω，其中M为水轮机力矩，ω为水轮机旋转角速度；Q为机组流量；ΔH为发电水头.

水轮机单位参数表达式为

(8)

式中：Q11为单位流量；n11为单位转速；D1为转轮直径；n为机组转速.

在给定出力、水头的条件下，根据式(7)，(8)以及水轮机模型特性曲线试算出机组不同运行转速对应的发电效率，得到相同水头和出力下转速与发电效率的对应关系如图1所示.

图1 初始运行转速与发电效率对应关系曲线

由图1可以看出，同一水头和出力条件下发电效率随着转速的升高而降低.其中，机组在最大发电水头Hmax额定出力条件下转速降低为最小运行转速允许值时，发电效率相较于额定转速条件下提高1.43%；运行转速升高至最大转速允许值时，发电效率相较于额定转速条件下降低3.20%.机组在额定水头Hr下额定出力运行，降低运行转速低于额定转速，发电效率提高不明显；初始运行转速为最大转速允许值时，发电效率相较于额定转速运行时下降3.63%.最小发电水头hmin条件下，运行转速对发电效率的影响明显，最大运行转速与最小运行转速条件下发电效率相差11.46%.

由于低水头工况不是水锤压力和转速最大上升率的控制工况，为分析运行转速的改变对机组调保参数的影响，选取高水头和额定水头工况进行甩负荷过渡过程计算：① 工况T1：最大发电水头2台机组额定出力运行，突甩负荷，导叶正常关闭；② 工况T2：额定水头，额定流量，2台机额定出力运行，突甩负荷，导叶正常关闭.导叶关闭规律选用斜率为1/26一段直线关闭规律(即相对开度从1关至0用时26 s).

2个工况中分别选取额定转速ne,0.90ne,0.95ne,1.05ne和1.10ne这5个初始转速探究其对调保参数的影响.其中，0.90ne,0.95ne,1.05ne和1.10ne分别为337.50，356.25，393.75，412.50 r/min.

2.3 初始转速对甩负荷过渡过程的影响及分析

选取2.2节中的计算工况和初始运行转速边界条件，工况T1和工况T2计算结果如图2，3所示,图中n0为初始转速；hc为蜗壳最大压力，hw为尾水最小压力；βm为转速最大上升率.

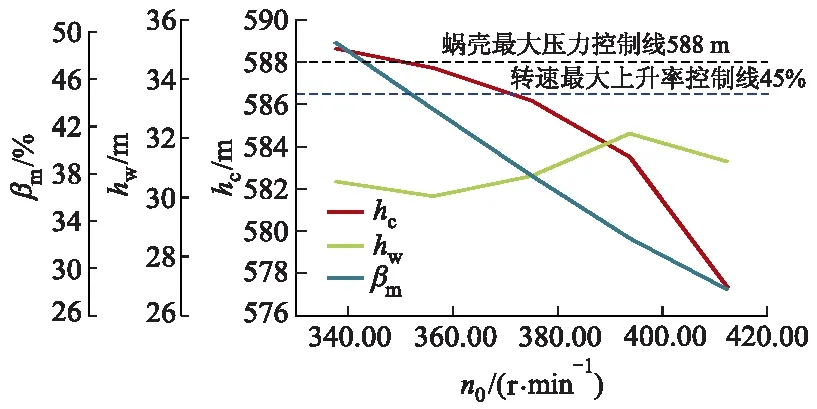
图2 工况T1蜗壳最大压力、转速最大上升率及尾水最小压力随初始运行转速变化过程

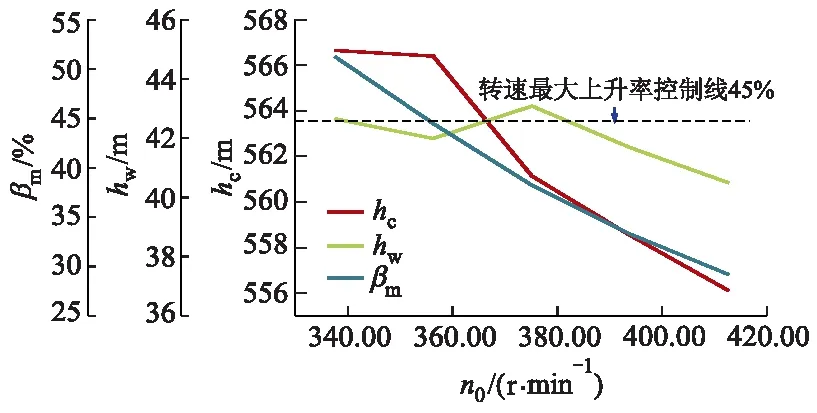
图3 工况T2蜗壳最大压力、转速最大上升率及尾水最小压力随初始运行转速变化过程

由图2，3可以看出，在最大发电水头和额定水头的条件下，甩负荷后蜗壳最大压力和转速最大上升率随机组初始运行转速的减小而增大，尾水最小压力无明显变化规律，且变化范围不大.

其中，最大发电水头条件下，机组最小运行转速337.50 r/min甩负荷后蜗壳最大压力与转速最大上升率均超过控制标准.额定水头条件下，机组初始运行转速337.50 r/min甩负荷后转速最大上升率超过控制标准.

因此，在本工程高水头和额定水头条件下，机组额定出力运行时初始运行转速在356.25～375.00 r/min选取，采用现有的斜率为1/26一段直线关闭规律能够满足调节保证计算控制标准且机组具有较高的发电效率.

下文以工况T1为例分析初始运行转速对机组甩负荷后蜗壳最大压力和转速最大上升率的影响原因.

根据水轮发电机组的运动方程[16]

(9)

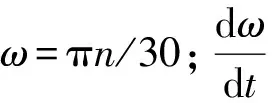
对等式两边积分，得到

(10)

式中：t0为甩负荷开始时刻点；t1为水轮机主动力矩为0时刻点；Δn为转速的上升值，右边的积分结果越大则转速上升值越大.

图4为事故甩负荷后不同初始运行转速条件下水轮机主动力矩Mt随时间变化曲线，从图中可以看出，力矩与时间曲线所包围的面积与初始运行转速成反比.在相同水头和出力条件下，初始运行转速越小，式(10)所求得的积分面积越大，即Δn越大.因此，初始运行转速越小，甩负荷后机组转速上升值越大，转速最大上升率越大.

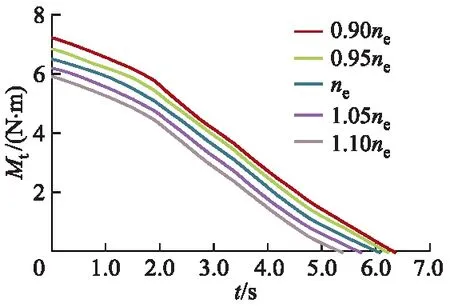
图4 工况T1不同初始转速条件下力矩随时间变化过程线

另一方面，水锤升压的产生主要来自流量的变化，抽水蓄能机组流量变化取决于开度和转速的双重影响[17]

(11)

式中：Q为机组流量；τ为导叶开度.

在机组导叶关闭初期，抽水蓄能机组特性曲线比较平缓，机组转速对流量的影响较小，即式(11)中第2项接近于0，水锤升压主要来自第1项中导叶关闭所产生的水锤正压波.随着甩负荷过程中机组转速不断增大，机组工况点靠近飞逸线附近，转速对流量变化的影响变大，此时水锤升压主要来自式(11)中2项的共同影响，水锤升压达到最大.

给出不同初始转速条件下稳态计算参数以及机组甩负荷后的流量变化率和蜗壳压力变化过程线，计算结果见表2、图5和图6，其中，Q0为初始流量，τ0为初始导叶开度，dQ/dt为流量变化率.

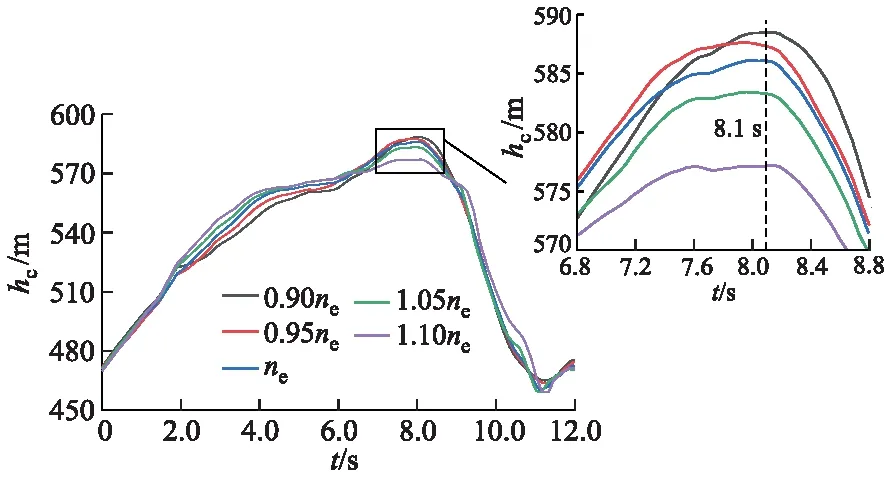
图6 工况T1不同初始运行转速条件下蜗壳压力随时间变化过程线

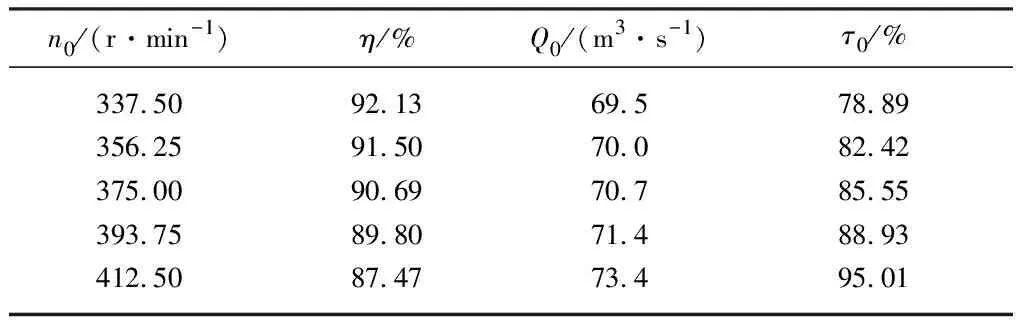
表2 工况T1不同初始转速条件下稳态计算参数

图5 工况T1不同初始运行转速条件下流量变化率随时间变化过程线

如表2中所示，初始运行转速越大，对应的初始流量和初始导叶开度越大.导叶关闭初期，水锤压力主要来自式(11)中第1项导叶关闭所产生的水锤正压波.因此，初始转速越大则甩负荷后导叶关闭初期流量变化率越大，水锤压力越大.

由图5，6可以看出，导叶关闭初始0～6.0 s，机组转速对流量的影响较小，较大的初始运行转速甩负荷后0～6.0 s流量变化率和蜗壳压力较大.

而6 s后水轮机工况点在飞逸点附近，转速对流量变化的影响变大，较小的初始运行转速在飞逸点附近造成较大的流量变化率，从而导致较大的蜗壳压力极值.造成图6局部放大图中，最小初始转速条件下甩负荷后蜗壳压力极值最大的原因主要来自式(11)中第2项转速对流量的影响.

图4中，初始运行转速越小，甩负荷后水轮机主动力矩减小为0的时间越长，即到达飞逸点的时间越长.根据水轮发电机组的运动方程，水轮机到达飞逸点后转速达到最大值.因此，相同条件下，机组初始运行转速越小，转速上升至飞逸点的时间越长.如图6局部放大图中所示，蜗壳最大压力出现的时刻点也相对较迟.

3 结 论

文中研究了可变速抽水蓄能机组不同初始转速对甩负荷过渡过程的影响，得到如下结论：

1)初始运行转速越小，事故甩负荷过程中，机组转速最大上升率和蜗壳最大压力越大，其原因在于不同起始运行转速条件下，机组的初始工况点发生变化，过渡过程中机组力矩和流量变化率发生变化.

2)在实际运行中，可变速抽水蓄能机组在降低运行转速、提高发电效率的同时，还需考虑降低转速对过渡过程的影响.