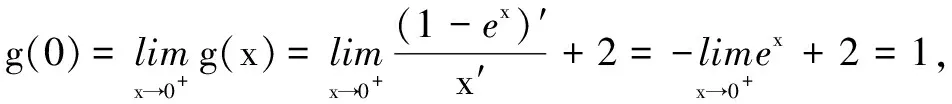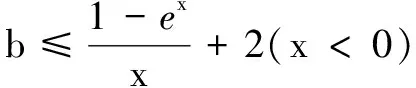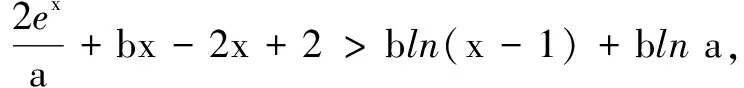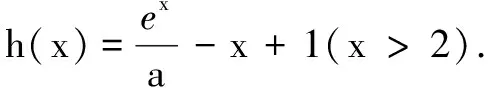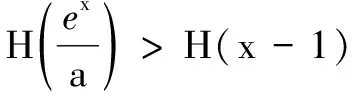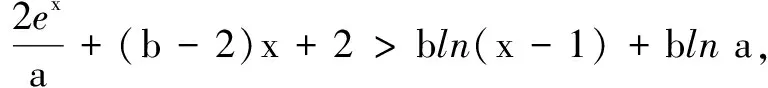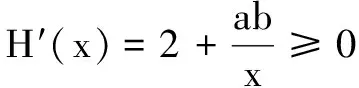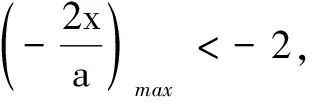透视命题意图 优选解题方向——以一道函数综合题的求解为例

黄启贤 陈益周

(福建省莆田第十中学351100) (福建省莆田第五中学351100)

命题的意图决定着解题的方向.透过命题意图，在多解中择优，就要从整体的视角探究试题，多角度转化试题条件，联系已有的知识与方法储备，探究试题命制意图，拟定解题方向.

一、试题呈现

(1)当a=2时，f(x)≥3恒成立，求b的值；

(2)当02时，f(x)>bln[a(x-1)]恒成立，求b的取值范围.

本题是2022年莆田市1月份高三质量检查题，探究函数不等式恒成立时参数的取值范围，体现基础性、综合性、创新型的考查要求，突出引导教学、服务选才的高考核心功能.

二、命题意图分析

在第(1)问中，条件整理后可转化为ex≥(2-b)x+1恒成立，题干经典精炼，从中可发现命题者是基于不等式ex≥x+1设计试题，意图考查ex≥x+1的灵活应用.再从不等式的简练角度来看，可看出命题者有意识地降低解题门槛，允许多角度解决问题.

在第(2)问中，试题函数是指数与对数混合的形式，命题者应是基于同构的思想设计问题，故采用同构法解题.而条件初步整理后可得2ex+abln ex>2[a(x-1)]+abln[a(x-1)]进一步印证了猜想.

三、解法探究

第(1)问是函数不等式的恒成立问题，仅包含一个参数b.在包含单参数的函数任意性与存在性问题中求参数的取值范围，通常采用参变分离策略.根据分离的程度，一般分成三类:完全分离，部分分离，不分离(即直接法).

其中部分分离法解题，切合命题意图.

第(2)问也是函数不等式的恒成立问题，此时包含两个参数.不等式中包含指数函数、对数函数等，结合指数对数之间可以转化的特性，常将不等式的左右两侧整理成结构一致的表达式(即同构法)来解题.

1.第(1)问解法探究

解法1(完全分离法)

当a=2时，f(x)≥3恒成立等价于

ex+(b-2)x-1≥0

①

恒成立.

当x=0时，① 式恒成立，b∈R.

令h(x)=(1-x)ex-1(x>0)，则h′(x)=-xex<0，h(x)单调减，h(x)

综上，b=1.

评注完全分离法是处理含参问题的优选方法.但从上述解答过程可以发现，因为要除以x，故需对x分成x=0，x>0,x<0三类情况讨论;另外因为分母是x，为得到g(x)的值域需引用洛必达法则求极限，增大了解题的运算量.显然用这种方法，会出现分类不全面、值域难以获取等问题，不是最优的解题方法.

解法2(部分分离法)

当a=2时，f(x)≥3恒成立等价于ex≥(2-b)x+1恒成立,即g(x)=ex的图象应在y=(2-b)x+1图象的上方(如图1).

因为g(x)=ex与y=(2-b)x+1的图象均过点(0,1)，所以y=(2-b)x+1应为曲线g(x)=ex在点(0,1)处的切线.

又g′(x)=ex，g′(0)=1,得g(x)=ex在点(0,1)处的切线方程为y=x+1.所以2-b=1，即b=1.

以下证明:ex≥x+1.

设h(x)=ex-x-1，则h′(x)=ex-1，由此易知h(x)在(-∞,0)单调减，在(0,+∞)单调增,所以h(x)≥h(0)=0，即ex≥x+1.

综上，b=1.

评注部分分离法是处理由较为明显两部分或两类函数组成的函数时采用的方法，强调数形结合的数学思想，过程简洁直观.另外经典的不等式模型也常作为分离的依据，如ex≥x+1,lnx≤x-1,sinx≤x(x≥0)等，或以上不等式的变式，如ex-1≥x,ln(x+1)≤x,ekx≥kx+1等.

解法3(直接法)

当a=2时，令g(x)=f(x)-3=ex+(b-2)x-1，则g′(x)=ex+b-2，原命题等价于g(x)≥0恒成立.

当b-2≥0，即b≥2时，g′(x)≥0，g(x)单调增.又g(0)=0，故x<0时，g(x)<0.不满足题意.

当b-2<0，即b<2时，由g′(x)≥0得x≥ln(2-b).故g(x)在(-∞,ln(2-b))单调减,在(ln(2-b),+∞)单调增，得g(x)≥g(ln(2-b))=(2-b)[1-ln(2-b)]-1.

设m=2-b>0，则y=(2-b)[1-ln(2-b)]-1(b<0)可化为t(m)=m(1-lnm)-1，由t′=-lnm≥0，得0

又g(x)≥0恒成立，故g(ln(2-b))=0，即m=2-b=1，得到b=1.

评注直接法即参数不分离，是参数和变量放置在等式或不等式的同一侧进行处理的方法，其解题过程主要有求导判断单调区间、根据单调性求值域或比较大小.主要数学运算体现在导数正负的分类判断，以及根据单调性作图以解决相应问题.

解法4(先猜后证)

当a=2时，令g(x)=f(x)-3=ex+(b-2)x-1，则f(x)≥3等价于g(x)≥0.

因为g(0)=0，所以x=0为g(x)的极小值点.又g′(x)=ex+b-2，故g′(0)=b-1=0，解得b=1.

当b=1时，g′(x)=ex-1，则当x∈(-∞,0)时，g′(x)<0，g(x)单调减;当x∈(0,+∞)时，g′(x)>0，g(x)单调增.所以g(x)≥g(0)=0，符合题意.

综上，b=1.

评注解法4也是直接法.它根据“求b的值”这一问题特征，采用先求存在性，再证唯一性的方法，有效减少了运算量.

2.第(2)问解法探究

②

恒成立.

评注本解法通过构造函数H(x)=2x+blnx，将原不等关系转化为两多项式间的不等关系与函数值之间的不等关系(这里两多项式看作两个变量)，再根据单调性与不等关系推导出H(x)的单调性，进而求出参数b的取值范围.

2ex+abln ex>2[a(x-1)]+abln[a(x-1)]

③

恒成立.

设h(x)=ex-a(x-1)(x>2),则h′(x)=ex-a>e2-a≥0，h(x)单调增，有h(x)>h(2)=e2-a≥0，即ex>a(x-1)>a.

评注本解法通过构造函数H(x)=2+ablnx来解题，过程及原理与解法1类似.另外，也可以将解法2中的③式，转化为2ex+abx>2elna(x-1)+abln[a(x-1)]，再构造函数H(x)=2ex+abx来解题.

综上,反思解题过程，试着从命题者的视角分析问题，弄清试题设计所涉及的背景、知识、方法并及时地归纳和完善相应的知识与方法体系，既能做到一题多解、多解择优，又可达到到多题一解、多解归一.