利用复数求解三角函数问题
方志平
(广东省惠州市第一中学,516007)
高中数学新教材增加了一节“复数的三角表示”选学内容,不仅加深了学生对复数几何意义的认识,而且能拓宽学生的解题思路.从复数的三角形式z=r(cosθ+isinθ),我们能够分析出复数和三角函数之间是存在着密切关系.本文分类例说利用复数求解与三角有关的问题,希望能够给学生在解决一些三角问题时多一条思路.
一、求三角函数值
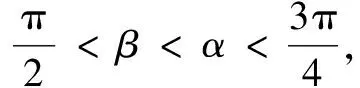
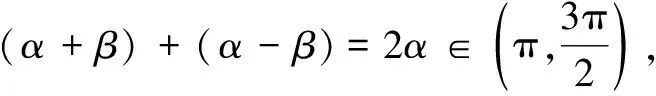
评注本题也可采用配角法2α=(α+β)+(α-β)求解,而上述解法则给学生提供了一种新颖的解法.
例2已知cosA+cosB+cosC=0,sinA+sinB+sinC=0,求sin 2A+sin 2B+sin 2C和sin2A+sin2B+sin2C的值.
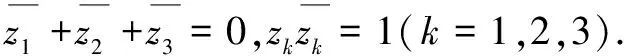
=(z1+z2+z3)2-2(z1z2+z2z3+z3z1)
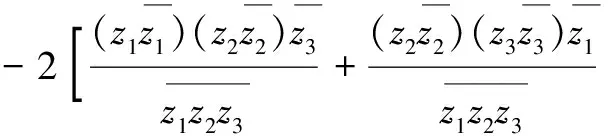
=0.
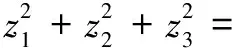

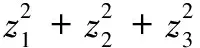
二、证明三角恒等式
例3证明: cos 3α=4cos3α-3cosα,sin 3α=3sinα-4sin3α.
证明由棣莫弗定理,得(cosα+isinα)3=cos 3α+isin 3α.
又由(cosα+isinα)3=cos3α+3cos2α·(isinα)+3cosα(isinα)2+(isinα)3=(4cos3α-3cosα)+(3sinα-4sin3α)i,根据复数相等的定义,得
cos 3α=4cos3α-3cosα,
sin 3α=3sinα-4sin3α.
评注本解法借用棣莫弗定理进行证明,旨在拓展学生解题思路,感受巧用复数三角形式解题的神奇魅力!
再看一例.
例4证明:
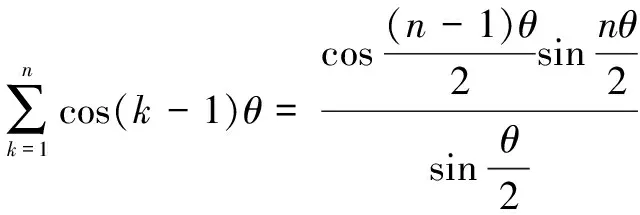
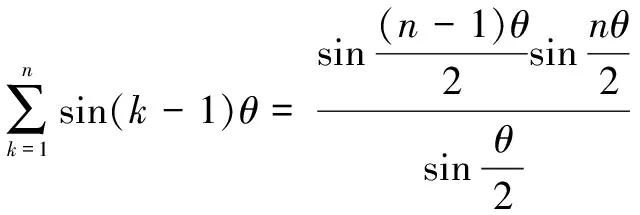
证明由棣莫弗定理,可得(cosθ+isinθ)n=cosnθ+isinnθ.
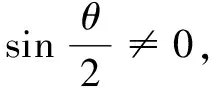
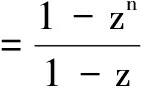
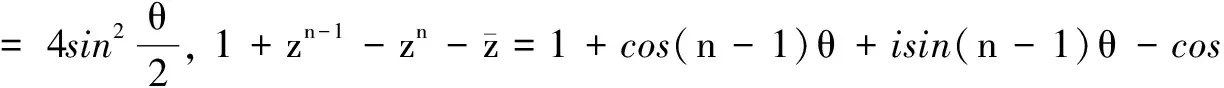
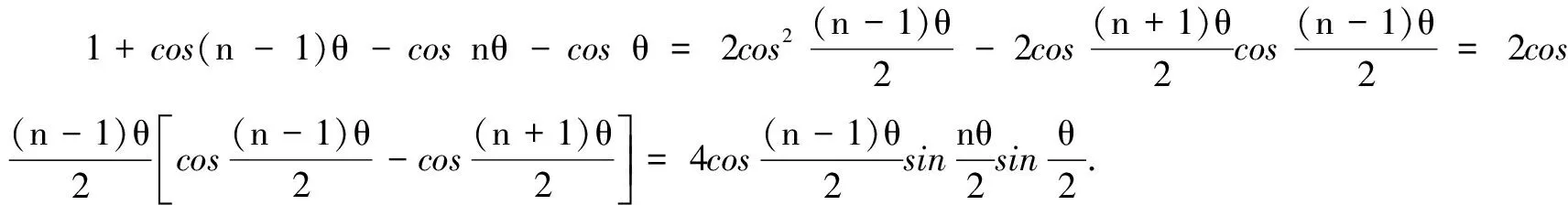
A+Bi

综上,由两复数相等的定义,可得结论成立.
三、证明三角不等式

证明由于
+|sinα|i)(|cosα|-|sinα|i)]

两边取模并放缩,易见
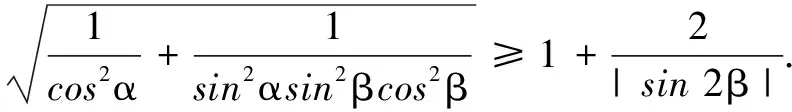
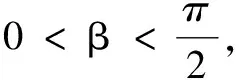
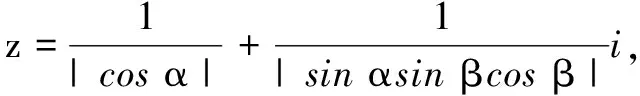
例6已知α为锐角,证明:
证明由于

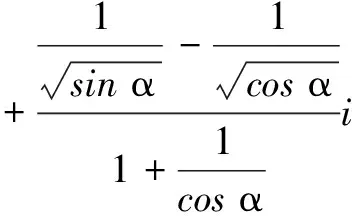
两边取模并放缩,可得
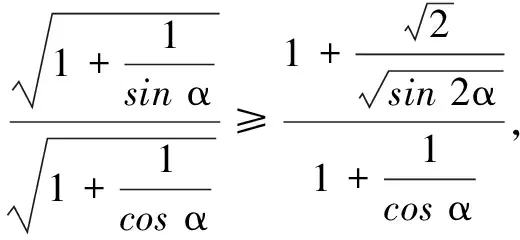
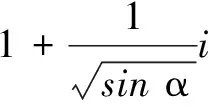
四、求角的大小
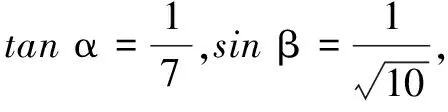
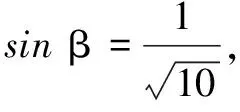
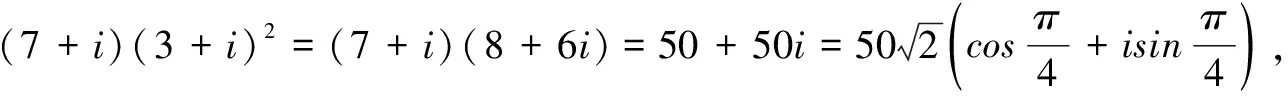
评注本题实质上是先寻求辐角为α的一个复数与辐角为β的另一个复数的平方之乘积,再寻找这个积对应复数的辐角主值.
例8如图1,已知平面内八个相等的正方形并列排放,求∠1+∠2+∠3+∠4的大小.

解建立坐标系如图1,由平行线对应的内错角相等,可知∠1是复数3+i的辐角的主值,∠2是复数5+i的辐角的主值,∠3是复数7+i的辐角的主值,∠4是复数8+i的辐角的主值.
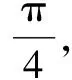
评注由图形的特殊性,不难求出分别以∠1,∠2,∠3,∠4为辐角主值所对应的一个复数,再由复数乘法几何意义知∠1+∠2+∠3+∠4就是这四个复数乘积的辐角主值
综上,尽管复数在高中数学中渐渐淡化,但只要我们进行深入学习和研究,就可以知道复数的内涵是非常丰富的,发挥其本质属性具有举足轻重的作用.

