车用千斤顶上支成形有限元分析及工艺优化

孙红磊，马世博，王伟，穆振凯，王奕博，赵军

车用千斤顶上支成形有限元分析及工艺优化

孙红磊1，马世博2，王伟2，穆振凯2，王奕博2，赵军1

（1.燕山大学 先进锻压成形技术与科学教育部重点实验室，河北 秦皇岛 066004；2.河北科技大学 河北省材料近净成形技术重点实验室，石家庄 050018）

解决千斤顶上支外缘不规则曲面混合翻边成形过程中容易出现的破裂等缺陷问题。基于Dynaform软件对千斤顶上支进行冲压仿真模拟，分析凸凹模圆角半径、凸凹模间隙、压边力对千斤顶上支成形的影响规律，并结合成形极限图、厚度变化云图等，采用控制变量法、正交实验对其工艺和参数进行优化。经有限元分析和正交优化的千斤顶外缘曲面翻边工艺如下：凸模圆角为过渡圆角结构，其齿顶大圆角和边缘小圆角半径分别为3.5 mm和0.7 mm，凹模圆角半径为3.5 mm，凸凹模间隙为2.8 mm，压边力为50 000 N。采用最佳工艺方案可生产出合格制件，实际成形件的减薄情况与模拟结果基本一致，所得成形工艺参数对制件的影响规律可为研究不规则曲面混合翻边成形提供一定的参考。

千斤顶上支；有限元模拟；外缘曲面翻边；正交实验

随着社会经济的发展，汽车工业的发展规模越来越大，对汽车维修辅助工具的要求也日趋提高。千斤顶作为汽车维修工的“生命支柱”，在汽车维修护理中发挥着至关重要的作用[1]。千斤顶上支的冲压成形过程涉及了许多物理现象，是一个具有高度非线性的弹塑性变形过程[2]。传统模具设计缺乏理论指导，只能依靠经验进行反复试模与调整，直至成形出合格零件，这一过程所需时间较长并且资金耗费严重[3]。

采用有限元技术进行分析优化可以加快产品的开发速度。专用板材成形仿真软件可以对现有模具的板材成形过程进行模拟分析，并得出符合实际的修调解决方案，提高产品的品质[4-6]。千斤顶上支是齿条千斤顶关键成形部件之一，其品质直接影响到千斤顶的使用年限，但因受实际加工的限制，其边缘曲线复杂，圆角要求严格，容易出现破裂，导致冲压成形难度较大[7-11]。冲压工艺的模具参数和工艺参数优化过程复杂，许多因素都直接或间接地影响成形结果。因此，通过成熟的仿真技术可以减少千斤顶上支成形的试模次数，降低开发所需成本，节约时间。同时，在一定条件下还可以使模具和工艺设计达到最佳配合，提高千斤顶上支产品的成形品质[12-14]。

文中基于Dynaform软件进行千斤顶上支外缘曲面翻边模拟，在分析各工艺参数对制件影响规律的基础上，结合正交优化方法[15]，给出能获得理想成形制件的工艺方案及参数。

1 千斤顶上支结构分析

图1为280B千斤顶上支，材料为SAPH440，厚度为2.0 mm，化学成分如表1所示，SAPH440的抗拉强度≥440 MPa，屈服强度≥305 MPa，伸长率≥30%。该制件冲压工序包括落料、内圆孔翻边、外缘曲面翻边和冲孔。落料和冲孔为简单工艺，冲压成形中不易产生缺陷。成形缺陷主要产生于内圆孔翻边和外缘不规则曲面混合翻边过程，文中主要针对外缘不规则曲面混合翻边工序进行研究。

图1 千斤顶上支件

表1 SAPH440化学成分

Tab.1 Chemical composition of SAPH440 wt.%

在成形过程中，当未变形区的材料难以流动至齿顶处时会造成齿顶破裂，如图1所示的画圈区域，这主要与模具结构及工艺参数有关。为此，文中将利用Dynaform软件对外缘不规则曲面混合翻边工序进行仿真模拟，探究最佳成形工艺参数。通过工艺补充构建了千斤顶上支外缘曲面翻边的有限元模型，如图2所示。工具采用壳体单元，板料采用实体单元。工具网格最大尺寸为1.0 mm，最小尺寸为0.25 mm，板料单元尺寸为0.5 mm，板料用坯料生成器划分网格。

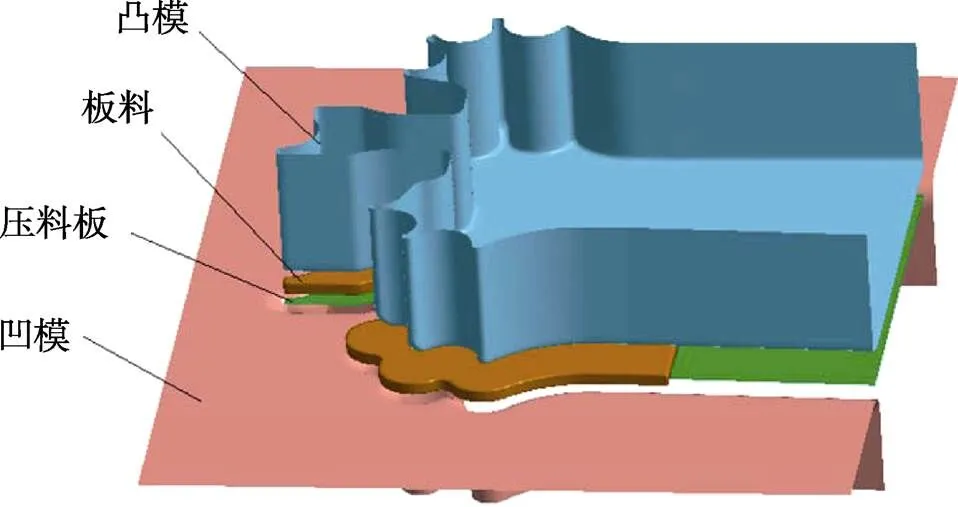
图2 外缘翻边有限元模型

2 不同参数对制件成形影响

由成形过程可知，影响材料流动的主要因素为齿顶开裂处的凸模圆角结构及尺寸。齿顶处凸模圆角较小会限制翻边过程中材料的流动，导致齿顶处材料无法顺利流动至凸缘处，进而造成齿顶变形不均匀，当变形超出材料允许塑性变形范围时就会产生开裂。除此之外，压边力、模具间隙对成形质量同样有着重要影响。为此，文中将着重研究凸模圆角结构及尺寸、凹模圆角半径、压边力、模具间隙4个工艺参数对上支外缘翻边的影响规律，并通过正交实验进行优化分析，给出最优工艺方案。

2.1 各参数值的初步确定

压边力一般采用式（1）所示的经验公式进行确定。

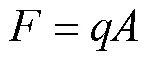
式中：为压边圈压力，N；为单位面积压边力，一般取2～4.5 MPa；为压边圈下的投影面积，mm2。经测量，板料压边面积为22 800 mm2，则预估压边力为102 600 N。根据经验及文献[15]，摩擦因数一般取0.1，冲压速度取2 000～5 000 mm/s，模具间隙一般取坯料厚度的1.1倍。

理论上模具的圆角半径越大，越利于翻边成形，越不易产生缺陷，但圆角结构和尺寸需结合上支制件的结构和尺寸确定。圆角结构可设置为如图3所示的整体圆角和过渡圆角（齿顶大圆角+边缘小圆角）2种结构。对于整体圆角结构，其圆角半径设置较大会导致齿宽变窄（最小齿宽为2.0 mm，圆角半径大于0.5 mm），加剧边缘材料变形程度，使其易于开裂。整体圆角半径过小时，凸凹模圆角接触区域的变形近似剪切变形（0.15～0.25 mm），不利于坯料的流动。过渡圆角结构则包含齿顶大圆角和边缘小圆角2个部分，根据零件结构需求，齿顶大圆角的半径可设置为2～4.0 mm（在拉深成形中，凸模圆角半径大于坯料厚度时易于未发生变形的材料流入变形区）。齿顶边缘处的变形近似弯曲变形，因此，边缘圆角最小半径应不小于0.25倍的壁厚。

综上分析，各工艺参数设定如表2所示。其中，用1表示过渡圆角结构的半径，1（3.5+0.7）表示过渡圆角结构中齿顶大圆角半径为3.5 mm，边缘小圆角半径为0.7 mm；用2表示整体圆角结构的半径，20.2表示整体圆角结构中的圆角半径为0.2 mm。通过在Dynaform软件中设置上述工况参数，分析不同工况下成形和减薄变化规律。

图3 凸模圆角结构形式

表2 各工艺参数设定

Tab.2 Condition setting of parameters

2.2 凸凹模间隙

分析该制件外部轮廓成形过程可知，齿顶区成形属于不规则曲面混合类翻边（同时包含外凸压缩类和内凹伸长类翻边）。压缩类曲面翻边指的是在板料的曲面部分，沿其边缘向曲面的曲率中心方向翻起竖边的成形方法，翻边过程中，凸缘内（侧壁）产生压应力，易发生失稳起皱；伸长类曲面翻边是指在板料的曲面部分，沿其边缘向曲面的曲率中心相反的方向翻起一定高度的成形方法，在成形中凸缘内产生拉应力而易破裂。因此，对于伸长类翻边，较大的间隙可以减小开裂的趋势；对于压缩类翻边，较小的间隙对防止起皱有利。为了探究不同凸凹模间隙对制件成形的综合影响，按表2中工况1的工艺参数进行模拟。不同凸凹模间隙下所得制件厚度分布如图4所示，凸凹模间隙对制件最小厚度的影响规律如图5所示。

随着凸凹模间隙的增大，成形后制件的最小厚度值也随之增大，制件的减薄趋势降低，表明在合理的凸凹模间隙条件下，伸长类翻边在该齿顶区的混合翻边中占主导作用。然而，随着凸凹模间隙的增大，起皱趋势会越来越显著，因此，在满足条件的情况下，凸凹模间隙应尽量小。

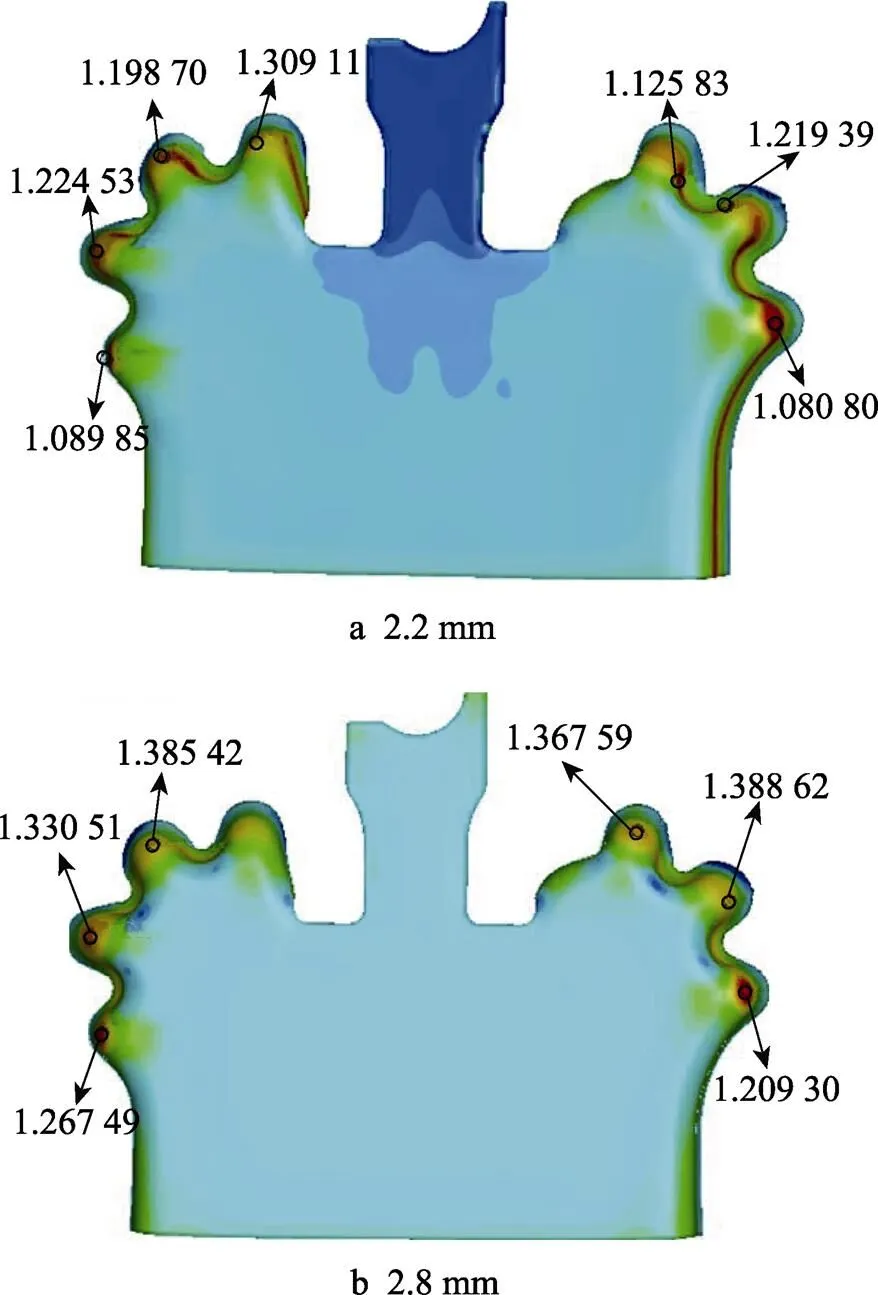
图4 不同凸凹模间隙下的厚度分布云图（mm）

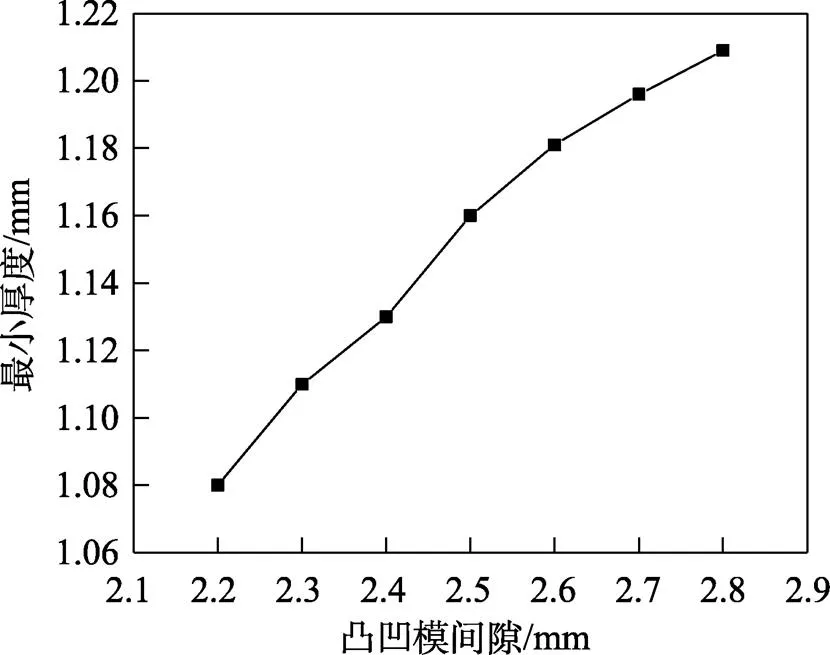
图5 凸凹模间隙对板料最小厚度的影响规律

2.3 压边力

压边力对金属流动和应力–应变分布具有重要影响，是成形时的重要参数之一[16]。压边力太大会增加危险断面的拉应力，导致拉裂或严重减薄，太小则防皱效果不好。根据表2中工况2的工艺参数进行模拟，所得不同压边力下的制件厚度分布如图6所示，压边力对制件最小厚度的影响规律如图7所示。

图7表明，当压边力增大时，板料的最小厚度先减小后增大。压边力增大，材料的流动阻力增大，减薄趋势随之增大。但是在外缘曲面翻边中，压边圈压住的板料并不直接参与翻边成形，所以当压边力增大到一定值时，板料就不再继续减薄了。

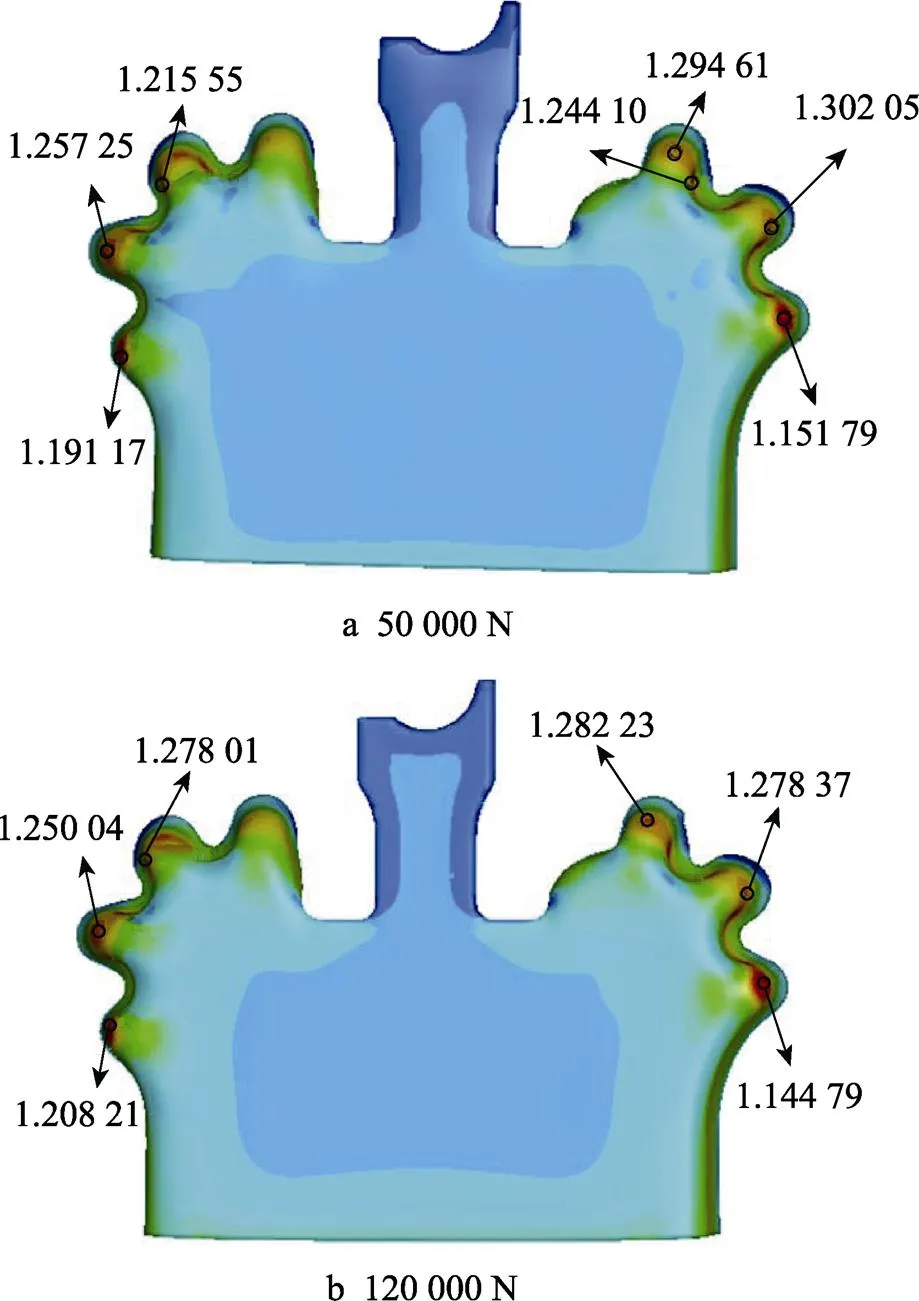
图6 不同压边力下的厚度分布云图（mm）

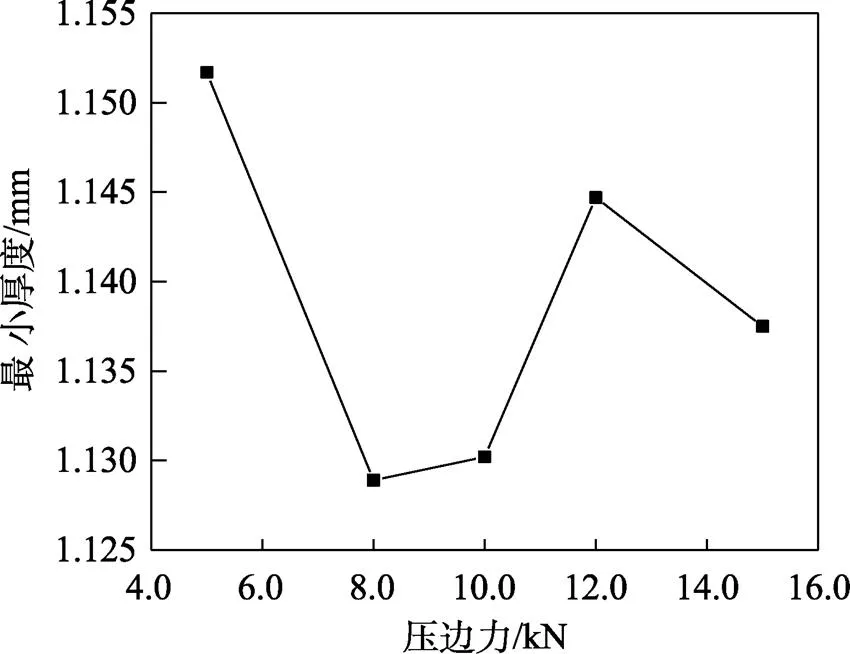
图7 压边力对板料最小厚度的影响规律

2.4 凹模圆角半径

凹模圆角半径是影响成形质量的一个重要参数。凹模圆角半径过小，板料在此处会受到较大的变形阻力，从而引起过度减薄直至拉裂；凹模圆角半径过大则会减小压边面积，在拉深后期，毛坯外缘过早离开压边圈容易产生起皱。根据表2中工况3的工艺参数进行模拟，研究不同凹模圆角半径下的制件减薄规律。不同凹模圆角半径下所得制件厚度分布如图8所示，凹模圆角半径对制件最小厚度的影响规律如图9所示。

图9表明，随着凹模圆角半径的增加，板料的最小厚度随之增大，板料的减薄趋势降低。但是随着凹模圆角半径的增大，起皱趋势越来越显著。因此，在满足条件的情况下，凹模圆角半径应尽量小。

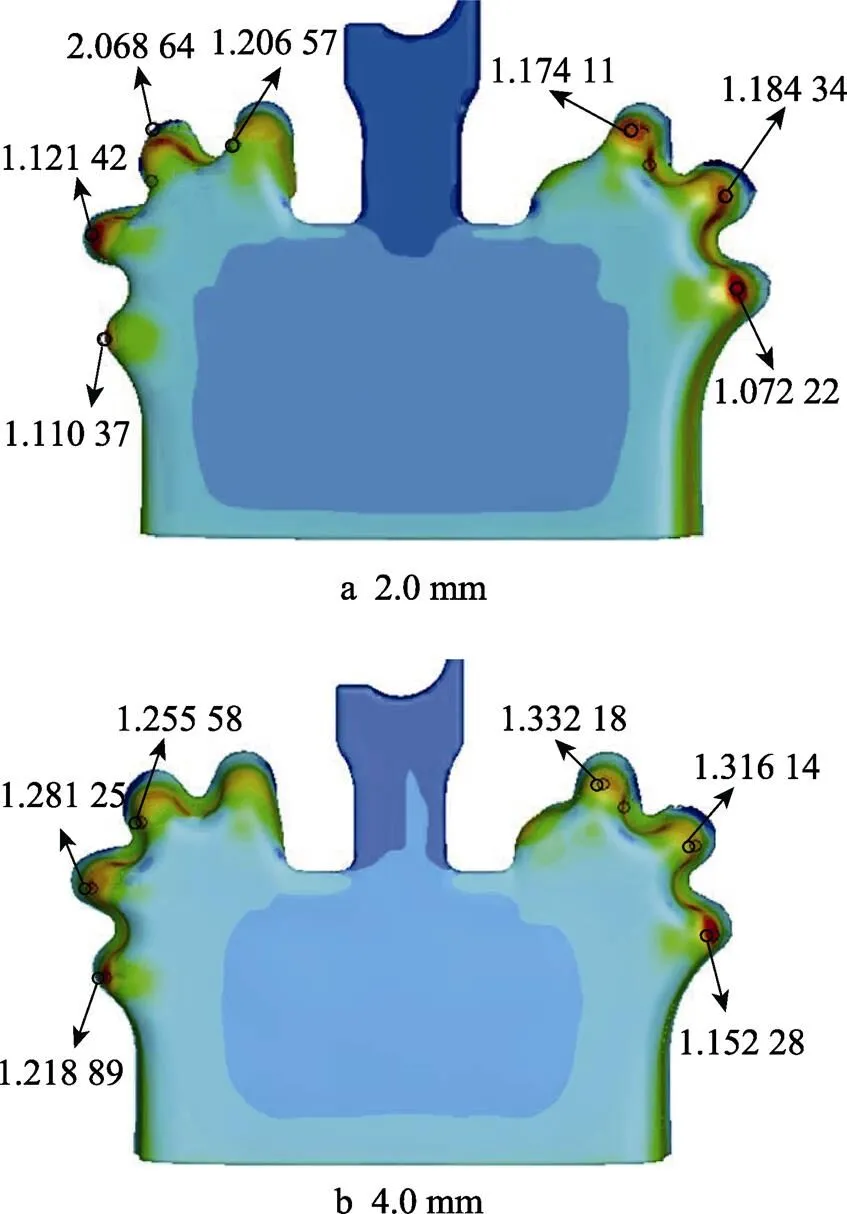
图8 不同凹模圆角半径下的厚度分布云图（mm）

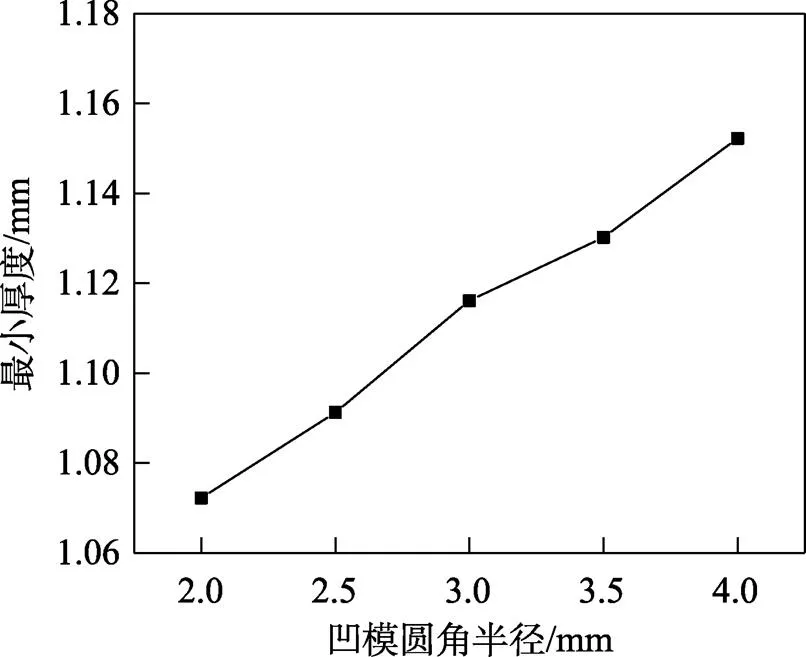
图9 凹模圆角半径对板料最小厚度的影响规律

2.5 凸模圆角半径

凸模圆角在千斤顶上支外缘翻边成形中起着十分重要的作用。凸模圆角如果过小，会使板料在该部位受到过大的弯曲变形，降低板料在危险处的强度，导致该部位板料严重减薄或拉裂。模拟时选择第1节中介绍的2种凸模圆角结构，探究不同结构及尺寸对成形结果的影响。整体圆角半径2分别选择0.2、0.5、0.8 mm，过渡圆角半径1分别选择（2+0.2）、（3.5+0.5）、（3.5+0.7）mm。不同凸模圆角结构及尺寸下所得制件厚度分布如图10所示，凸模圆角结构及尺寸对制件最小厚度的影响规律如图11所示。

图10 不同凸模圆角结构及半径下的厚度分布云图（mm）

图11 凸模圆角半径对板料最小厚度的影响规律

根据图11可知，凸模圆角的结构形式对制件最小厚度的影响大于圆角半径的影响。采用整体圆角结构时，所得制件的最小厚度值较小，破裂趋势严重；随着整体圆角半径的增大，所得制件的最小厚度值也随之增加，但仍在1.0 mm以下，由此判断，采用整体圆角结构是不可行的。当采用过渡圆角结构时，制件的最小厚度值在1.0 mm以上，随着齿顶大圆角和边缘小圆角半径值的增加，所得制件的最小厚度也逐渐变大，破裂趋势降低。

3 千斤顶的多因素正交优化分析

3.1 正交实验方案

正交实验是分析多因素、多水平的一种实验设计方法，通过极差分析法可得出各因素对实验指标影响的主次关系。根据上述分析，选择凸凹模间隙、压边力、凹模圆角半径、过渡圆角结构下的凸模圆角半径为影响因素，设计如表3所示的正交实验方案。文中暂不考虑各因素之间的交互作用，并以制件的减薄最小为优化目标，探究最优工艺参数组合。

表3 正交实验方案

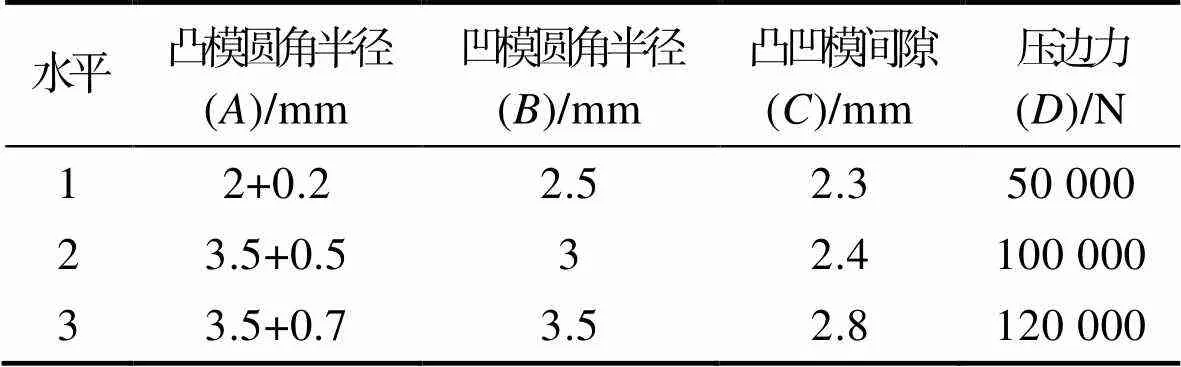
Tab.3 Orthogonal test scheme

3.2 正交实验结果分析

以上述4个因素作为研究因素，每个因素设置3个水平，选择正交表L9（34）进行实验。实验方案和结果如表4所示。采用极差分析法分析表4中的数据，结果如表5所示，其中1代表某因素对应水平1时制件最小厚度之和的平均值，2代表某因素对应水平2时制件最小厚度之和的平均值，3代表某因素对应水平3时制件最小厚度之和的平均值，为极差，其大小体现了各因素对实验结果的影响大小，极差越大，表明因素对实验指标的影响越大。为了直观分析，给出了如图12所示的各因素不同水平值与制件最小厚度关系。

表4 正交实验表及结果

Tab.4 Orthogonal test table and results

表5 正交实验极差分析

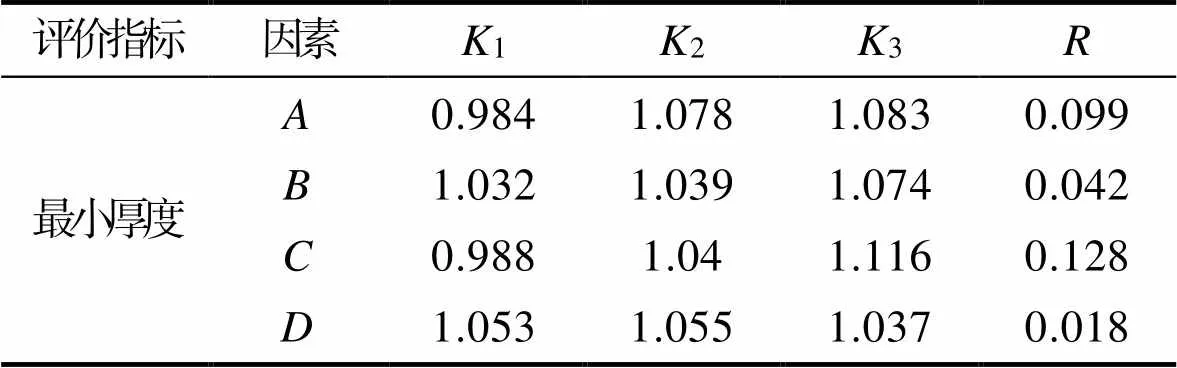
Tab.5 Range analysis results of orthogonal test mm

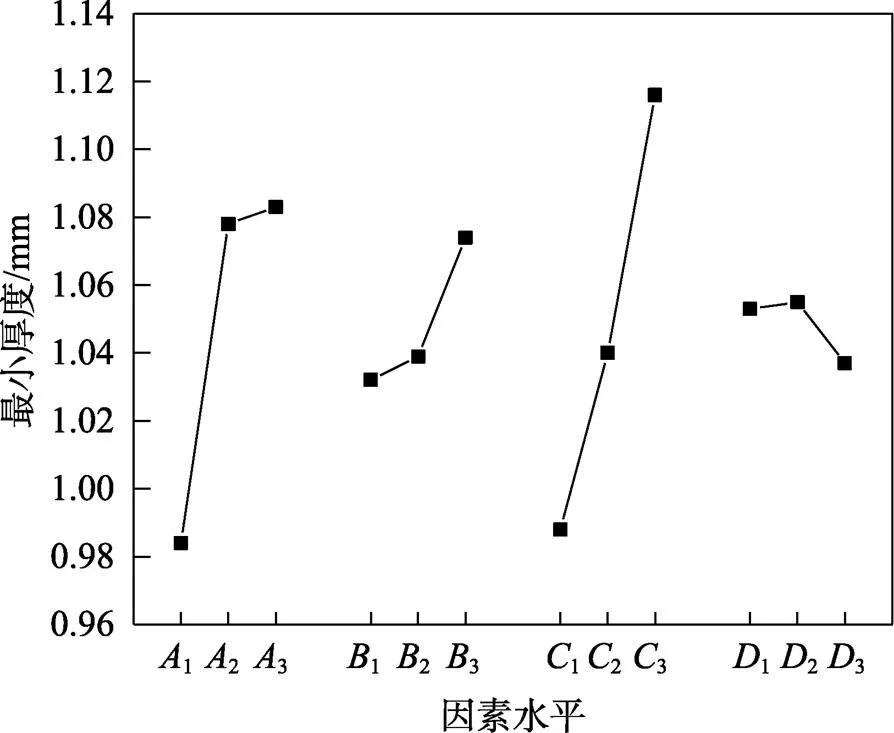
图12 各因素水平与最小厚度关系

分析数据可知，影响板料最小厚度的因素主次为>>>。随着凸模圆角半径（）的增加，制件的最小厚度呈现先陡增后趋于平缓的变化规律；随着凹模圆角半径（）的增加，制件的最小厚度值也相应有所增加，但其整体增加的幅值相对于凸模圆角半径所产生的变化较小；凸凹模间隙（）对制件最小厚度的影响最为显著，随着凸凹模间隙的增大，制件的最小厚度值近似呈线性增加；对于压边力（），制件的最小厚度随着压边力的增大呈现出先增大后减小的变化规律，且整体变化趋势不明显。

3.3 优化结果分析

根据图12，以各因素使减薄最小为依据得出最佳优化组合为3331，其中，1和2条件下的减薄相差很小，从工艺和设备角度考虑，选择压边力相对较小的1。采用凸模圆角半径为（3.5+0.7）mm的过渡圆角结构，凹模圆角半径为3.5 mm、凸凹模间隙为2.8 mm、压边力为50 000 N的工艺参数进行模拟，所得制件厚度分布如图13所示。

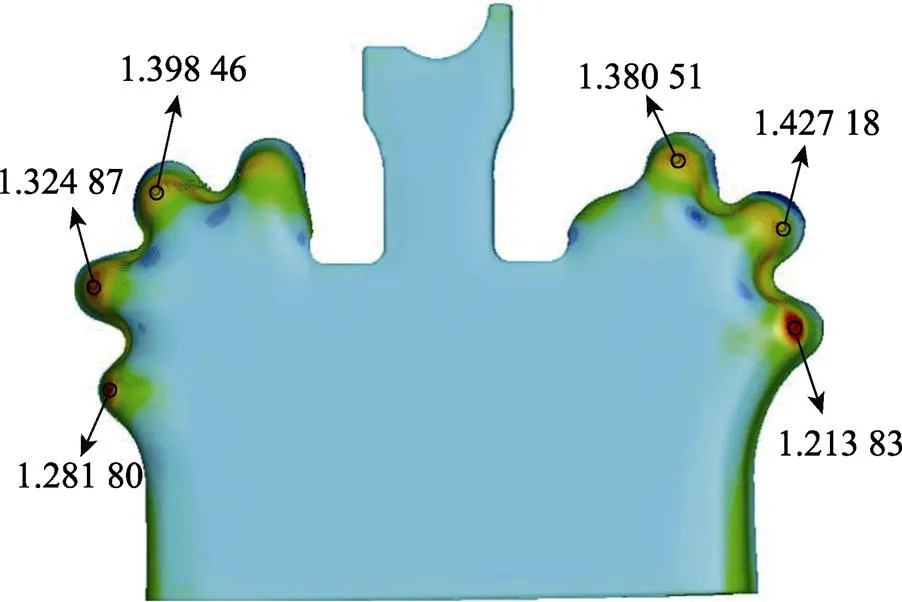
图13 最优工艺参数所得厚度分布（mm）

从图13可以看出，千斤顶上支外缘成形良好，制件最小厚度为1.21 mm，满足成形质量要求。利用上述有限元模拟优化的工艺参数进行千斤顶上支冲压成形验证实验，得到实际的成形零件如图14所示。从图14可以看出，该千斤顶上支件的整体成形质量较好，测量所得制件的最小厚度为1.08 mm，实验结果与有限元模拟结果相比，最小厚度的误差为12%，符合制件评价标准。制件的外缘翻边区域无成形缺陷，验证了正交实验和有限元分析的可靠性。

图14 千斤顶上支实物

4 结论

对千斤顶外缘翻边进行了Dynaform模拟分析，探究了凸模圆角结构及半径、凹模圆角半径、凸凹模间隙、压边力对外缘曲面翻边成形的影响规律，采用正交实验方法进行了参数优化，并得到了成形的最佳工艺参数组合。

凸模圆角结构对外缘翻边影响很大，优化整体圆角不能消除破裂缺陷，采用过渡圆角结构可有效降低减薄趋势。凸凹模间隙对成形影响也比较大，取值应适宜。压边力取值在实际生产的基础上上下浮动均可。凹模圆角对该工艺成形影响较小。正交优化的参数组合如下：凸模圆角为过渡圆角结构，且其齿顶大圆角和边缘小圆角半径分别为3.5 mm和0.7 mm，凹模圆角半径为3.5 mm，凸凹模间隙为2.8 mm，压边力为50 000 N。

[1] 张帅. 郑州市汽车维修行业的现状与发展[D]. 郑州: 河南农业大学, 2013: 2-5.

ZHANG Shuai. The Current Situation and Development of the Auto Repair Industry in Zhengzhou City[D]. Zhengzhou: Henan Agricultural University, 2013: 2-5.

[2] 赵广涛, 袁志鹏, 吴彦骏. QP980钢后纵梁冲压工艺优化[J]. 锻压技术, 2020, 45(4): 62-69.

ZHAO Guang-tao, YUAN Zhi-peng, WU Yan-jun. Optimization of Stamping Process for QP980 Steel Rear Side Member[J]. Forging & Stamping Technology, 2020, 45(4): 62-69.

[3] SU Hong-liang, HUANG Liang, LI Jian-jun, et al. Inhomogeneous Deformation Behaviors of Oblique Hole-Flanging Parts during Electromagnetic Forming[J]. Journal of Manufacturing Processes, 2020, 52: 1-11.

[4] PANTHI S K, RAMAKRISHNAN N, PATHAK K K, et al. An Analysis of Springback in Sheet Mental Bending Using Finite Element Method (FEM)[J]. Journal of Materials Processing Technology, 2007, 186(1/2/3): 120-124.

[5] FIRAT M, METE O H, KOCABICAK U, et al．Stamping Process Design Using FEA in Conjunction with Orthogonal Regression[J]. Finite Elements in Analysis and Design, 2010, 46(11): 992-1000.

[6] LIN Zhong-qin, WANG Wu-rong, CHEN Guan-long. A New Strategy to Optimize Variable Blank Holder Force Towards Improving the Forming Limits of Aluminum Sheet Metal Forming[J]. Journal of Materials Processing Technology, 2007, 183: 339-346.

[7] 欧航, 安浩, 孙式进, 等. 5182铝合金椭圆孔电磁翻边数值模拟研究[J]. 精密成形工程, 2021, 13(4): 9-15.

OU Hang, AN Hao, SUN Shi-jin, et al. Numerical Simulation Study on Oblique Hole-Flanging with 5182 Aluminum Alloy Produced by Electromagnetic Forming(EMF)[J]. Journal of Netshape Forming Engineering, 2021, 13(4): 9-15.

[8] MERKLEIN M, HAGENAH H. Introduction to Sheet-Bulk Metal Forming[J]. Production Engineering, 2016, 10(1): 1-3.

[9] 邱立, 田茜, 吴伟业, 等. 基于磁场变换器的双向加载式管件电磁翻边成形效果研究[J]. 精密成形工程, 2022, 14(3): 17-24.

QIU Li, TIAN Xi, WU Wei-ye, et al. Electromagnetic Flanging Forming Effect of Bidirectional Loading Tube Fittings Based on Magnetic Field Shaper[J]. Journal of Netshape Forming Engineering, 2022, 14(3): 17-24.

[10] 唐季平, 孙风成, 张容, 等. 某汽车燃料箱隔热板翻边成形工艺设计及研究[J]. 精密成形工程, 2022, 14(2): 39-45.

TANG Ji-ping, SUN Feng-cheng, ZHANG Rong, et al. Design and Study of Flanging and Forming Process of Automotive Fuel Tank Insulation Panel[J]. Journal of Netshape Forming Engineering, 2022, 14(2): 39-45.

[11] SUBRAMANIAM S, NATARAJAN B, PONAPPA K. Assessment of Dynamic Crushing and Energy Absorption Characteristics of Thin-Walled Cylinders Due to Axial and Oblique Impact Load[J]. Steel and Composite Structures, 2018, 28(2): 179-194.

[12] 谢映光, 梁满朝, 王成磊, 等. 铝合金控制臂锻造工艺及模具有限元模拟优化[J]. 锻压技术, 2021, 46(7): 7-13.

XIE Ying-guang, LIANG Man-chao, WANG Cheng-lei, et al. Optimization on Forging Process and Die for Aluminum Alloy Control Arm Using Finite Element Simulation[J]. Forging & Stamping Technology, 2021, 46(7): 7-13.

[13] KUMAR S, AHMED M, PANTHI S K. Effect of Punch Profile on Deformation Behaviour of AA5052 Sheet in Stretch Flanging Process[J]. Archives of Civil and Mechanical Engineering, 2020, 20(1): 1-17.

[14] 邓长勇, 董绍江, 谭伟. 某新能源汽车轻量化地板件冲压成形参数设计及优化[J]. 锻压技术, 2018, 43(10): 68-71.

DENG Chang-yong, DONG Shao-jiang, TAN Wei. Design and Optimization on Stamping Parameters for Lightweight Floor Parts of a New Energy Vehicle[J]. Forging & Stamping Technology, 2018, 43(10): 68-71.

[15] 臧其其, 闫华军, 张双杰, 等. 基于Dynaform的铝合金汽车地板梁成形分析及工艺参数优化[J]. 塑性工程学报, 2019, 26(2): 125-131.

ZANG Qi-qi, YAN Hua-jun, ZHANG Shuang-jie, et al. Forming Analysis and Process Parameters Optimization for Automobile Aluminum Alloy Floor Beam Based on Dynaform[J]. Journal of Plasticity Engineering, 2019, 26(2): 125-131.

[16] YAGAMI T, MANABE K, YAMAUCHI Y. Effect of Alternating Blank Holder Motion of Drawing and Wrinkle Elimination on Deep-Drawability[J]. Journal of Materials Processing Technology, 2007, 187/188: 187-191.

Finite Element Analysis and Process Optimization of Forming on Automobile Jack's Upper Stent

SUN Hong-lei1, MA Shi-bo2, WANG Wei2, MU Zhen-kai2, WANG Yi-bo2, ZHAO Jun1

(1. Key Laboratory of Advanced Forging & Stamping Technology and Science, Ministry of Education, Yanshan University, Hebei Qinhuangdao 066004, China; 2. Hebei Key Laboratory of Material Near-net Forming Technology, Hebei University of Science and Technology, Shijiazhuang 050018, China)

In order to solve the problem of cracks and other defects in the forming process of mixed flanging with irregular surface on the outer edge of the Jack’s upper stent. Based on Dynaform software, the stamping simulation of Jack upper stent was carried out, and the influence laws of punch and die fillet radius, clearance between punch and die, and blank holder force on Jack upper stent forming were analyzed. Combined with forming limit diagram and thickness change cloud diagram, the process and parameters were optimized by control variable method and orthogonal test. After finite element analysis and orthogonal optimization, theouter edge flanging of the jack was as follows: The punch is a transition fillet structure, and the radius of the fillet at the root and the small fillet at the edge are 3.5 mm and 0.7 mm respectively; die fillet radius is 3.5 mm; clearance between punch and die is 2.8 mm; blank holder force is 50 000 N. Qualified parts can be produced by using the best process scheme. The thinning of the actual formed parts is basically consistent with the simulation results. The influence law of forming process parameters on parts obtained in this paper provides a certain reference basis for the study of mixed flanging forming of irregular surface.

jack's upper stent; finite element simulation; outer edge flanging; orthogonal test

10.3969/j.issn.1674-6457.2022.06.011

TG386.1

A

1674-6457(2022)06-0078-08

2022–01–18

国家自然科学基金（51975509）；河北省自然科学基金（E2021208025）；河北省高层次人才资助项目（A202101016）

孙红磊（1979—），男，博士，副研究员，主要研究方向为板材成形新工艺。

王伟（1986—），男，博士，讲师，主要研究方向为金属材料精密塑性成形工艺。

责任编辑：蒋红晨